基于微分博弈的政企合作数据开放策略研究

樊自甫 樊可欣

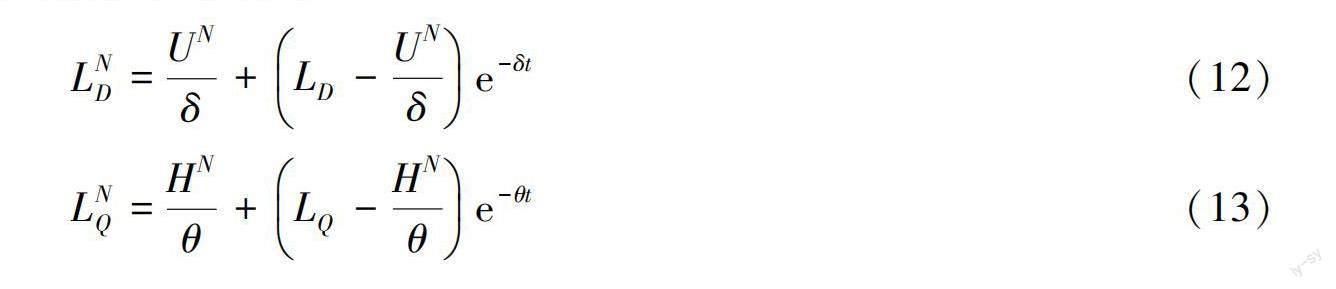
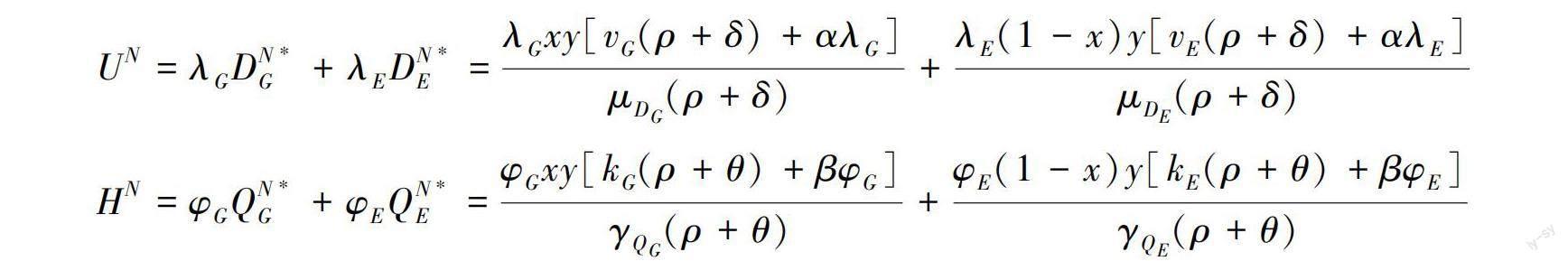
摘 要：数据作为一种关键生产要素，其开放、流通和利用水平直接影响着数字经济的发展。然而，现阶段我国的融合应用水平不高，政府和企业的数据开放力度以及数据开放质量仍有待加强。采用微分博弈方法，考虑数据开放程度和数据开放质量两个要素，构建以政府、企业为主体的Nash非合作博弈、Stackelberg主从博弈、协同合作博弈模型，根据HJB方程求解三种情形下的政企最优行为策略、最优数据开放程度、最优数据开放质量水平以及最优收益轨迹，并在时间一致性的条件下，探讨政企合作收益分配机制，最后对三种情形下的结论进行仿真分析。政府为企业分担成本可以促进社会数据开放程度及质量水平的提升，实现帕累托改善；且在协同合作情形下，数据开放程度、数据开放质量水平及政企总收益最高，可实现系统效益最大化。文章建立了科学有效的成本分担机制，为政企合作开放数据提供指导，并制定了长期稳定的收益分配机制，为政企协同合作提供基础。

关键词：数据开放程度；数据质量水平；政企合作；微分博弈；动态收益分配

中图分类号：F49文献标识码：A

文章编号：1673-8268（2023）05-0098-17

数字经济发展进入加速期，《中共中央关于坚持和完善中国特色社会主义制度 推进国家治理体系和治理能力现代化若干重大问题的决定》中，首次将数据列为生产要素之一^[1]。随着信息技术在社会经济各领域中的加速渗透，数字经济作为一种新型经济形态，日渐受到国内外学术界的关注，数据成为推动数字经济发展的要素之一^[2]。习近平总书记在党的十九大后第二次中央政治局集体学习会上指出：“加强政企合作，多方参与，加快公共服务领域数据集中和共享，推进同企业积累的社会数据进行平台对接，形成社会治理强大合力。”^[3]近年来，政府数据与企业数据的价值得到社会各界的广泛认同，截至2020年4月底，我国54.83%的省级行政区（不包含港澳台）、73.33%的副省级和32.08%的地级行政区都已推出了政府数据开放平台^[4]。政府是海量政府数据的产生者和保有者^[5]，企业是大量社会数据的采集者，大量的用户行为数据由企业掌握。数据开放共享、融合应用的需求逐步显现，但目前仍存在政企双方数据开放意愿不强、水平不足、质量难保障等诸多问题^[6-7]。

一、相關研究

目前，国内外学者针对数据开放的研究已经取得了一定成果，相关研究内容主要聚焦在以下几个方面：第一，利益相关者动力分析。对数据开放主体等进行界定与分类，运用利益相关者理论，解析不同利益相关者参与数据开放共享的动力，从不同类型利益的相关者视角探索政府数据开放价值的生成机制^[8-9]。第二，数据开放国际经验与中国路径。梳理美、英、澳、新等国家数据开放的先进经验，包括数据开放顶层设计、数据监管、创新措施、运行机制等，提出符合我国国情的数据开放路径，为我国数据开放提供理论与现实指导^[10-14]。第三，数据开放政策研究。对我国数据开放政策进行量化分析，发现了供给型、环境型和需求型等三类政策工具使用不均衡、内部不协调等问题，并提出了针对性的政策建议^[15]；研究发现我国有关数据开放政策还存在时效性不足、法治化程度不足等问题^[16]；从立法框架视角将现行政策与过去的政策进行对比，提出开放政府数据政策的意义^[17-19]。第四，数据开放质量研究。认为数据开放质量具有不确定性^[20]，运用文献分析法、规范分析法、SERVQUAL模型等方法对我国政府开放数据进行多维度评估，并提出了服务质量提升对策^[21-24]。近年来，部分学者基于政企合作视角研究数据开放问题，如魏益华等建立了政府参与的企业间数据共享演化博弈模型，得出企业共享意愿会因数据异质、企业间信任和违约金而增强的结论，指出政府监管对企业共享策略的影响较小，预评估数据质量、提高数据互补性、增强数据安全互信、构建战略合作、健全政策体系是促进企业数据共享的有效办法^[25]；黄如花等运用文献资料调查法和案例分析法分析美国政府数据开放共享的三种模式，结合我国数据开放现状总结了上述三种政府数据开放模式的优势^[26]。

梳理已有研究可以发现，现有文献大多从如何促进数据开放共享角度出发，或者考虑如何提升开放数据的质量，但是忽视了社会开放数据程度的两个决定因素，即数据开放程度与数据开放质量，且对于数据开放问题的研究多采用静态博弈的方法，鲜有文章采用动态微分博弈模型研究该问题，而政企合作数据开放是一个连续的动态博弈过程。考虑到微分博弈是一种能够研究双方或多方主体在连续时间内竞争与合作问题的动态博弈模型^[27]，故本文基于微分博弈模型，建立以政府和企业为主体的微分博弈模型，探讨三种情形下政企双方的最优努力程度、数据开放程度最优水平、数据开放质量最优水平以及最优收益，并设计在时间一致性条件下的收益分配机制以保障政企的稳定合作。

二、基本假设

本文考虑数据开放系统由政府（G）和企业（E）共同组成，均为理性主体，基本假设如下：

假设1：在数字经济背景下，D表示政府和企业在提高数据开放程度上所付出的努力，D_G、D_E分别表示政府、企业在提高数据开放程度上的努力程度（D_G≥0，D_E≥0），政府数据开放的成本C_DG与其努力程度D_G呈正相关关系，且边际成本与开放数据的努力程度成正比，即C′_DG（μ_DG）>0，C″_DG（μ_DG）>0。同理， C′_DE（μ_DE）>0，C″_DE（μ_DE）>0。政府和企业因提高数据开放水平而付出的成本函数表达式为

式（1）中：μ_DG、μ_DE分别表示政府、企业的数据开放成本系数，且μ_DG>0，μ_DE>0。

Q表示政府和企业在提高数据质量水平上付出的努力，Q_G、Q_E分别表示政府、企业为提高数据质量水平而付出的努力程度（Q_G≥0、Q_E≥0）。政府提高数据质量水平的成本Q_DG与其努力程度Q_G呈正相关关系，且边际成本与提高数据质量的努力程度成正比，即C′_QG（γ_QG）>0，C″_QG（γ_QG）>0;同理，C′_QE（γ_QE）>0，C″_QE（γ_QE）>0，因此政府和企业因数据开放而付出的成本函数表达式为

式（2）中：γ_QG、γ_QE分别表示政府、企业提高数据质量的成本系数，且γ_QG>0，γ_QE>0。

在数据开放过程中，政府作为企业的领导者，在提高数据开放程度及质量水平上的能力上要高于企业，这主要是由于政府具有资本及技术上的优势，为激励企业与政府合作，提升其数据开放程度及质量水平，政府可通过给予补贴、指导数据开放技术等方式为企业分担成本。假设政府在为企业提高数据开放程度上分担比例为ω_D的成本，且0<ω_D<1，政府在为企业提高数据质量水平上分担比例为ω_Q的成本，且0<ω_Q<1。

假设2：设L_D（t）表示t时刻社会上数据开放程度，数据开放程度指可以自由免费地访问、获取、利用数据的程度^[28]，由政府和企业在加大数据开放程度上的努力程度决定，是一个动态的变化过程，其变化规律满足如下微分方程

式（3）中：λ_G、λ_E分別表示政府、企业的提高数据开放活动对社会数据开放程度的影响系数，δ表示当政府和企业提高数据开放程度的努力均为0时，社会数据开放水平因时效性而导致的水平下降系数，且δ>0。

设L_Q（t）表示t时刻社会的数据质量水平，数据开放质量指数据可用性、数据完整性、数据及时更新、动态更新、数据请求和建议反馈^[21]，由政府和企业在提高数据质量水平上的努力程度决定，是一个动态的变化过程，其变化规律满足如下微分方程

式（4）中：φ_G、φ_E分别表示政府、企业的提高数据开放质量活动对社会数据质量水平的影响程度，θ表示当政府和企业提高数据质量的努力程度均为0时，社会数据质量因时效性而导致的质量下降系数，且θ>0。

假设3：政府和企业加大数据开放的力度会直接影响社会数据开放程度，且由于数据开放质量的提高可促进社会经济的发展，因而考虑数据开放程度和数据质量水平的共同影响，假设社会福利效应函数为

式（5）中：W₀表示社会初始的福利效应，ν_G、ν_E分别表示政府和企业提高数据开放程度的努力程度对社会福利效应的影响系数，k_G、k_E分别表示政府和企业提高数据质量水平的努力程度对社会福利的影响系数，α、β分别表示社会数据开放程度及质量水平对社会福利效应的影响系数。

假设4：政府和企业开放数据带来社会福利的增加使得公众对政府和企业的满意度大幅提升。且利用这些数据开发出的产品投入到市场后，能够发挥自身价值，并为政府和企业带来收益。令社会福利效应对政企开放数据收益的作用系数为y，y>0，则政府和企业开放数据带来的总收益为yW（t）。

政府和企业提高数据开放程度及质量水平的总收益在二者之间分配，分配比例分别为x，1－x，其中，00），两者目标都在无限时间区域内寻求自身收益最大化的最优策略。

综上假设，政府的目标函数公式如下

企业的目标函数公式如下

三、模型构建及求解

为探讨在不同情形下政府和企业的最优行为策略，将构建三个博弈模型，即Nash非合作博弈模型、Stackelberg主从博弈模型、协同合作博弈模型，分别用（N、S、C）标记。

（一）Nash非合作博弈（情形N）

在Nash非合作博弈情形下，政府和企业各自以自身利益最大化为目标，政府不为企业分担加大数据开放程度及提高质量水平的成本，即ω_D=0，ω_Q=0。在此情况下，政府和企业的目标函数公式如下

命题1：政府和企业在Nash非合作博弈中的最优策略分别为

数据开放程度、数据开放质量的最优水平分别为

式（12）和（13）中：U^N、H^N分别为

政府、企业的最优收益函数轨迹分别为

证明：为了得到非合作博弈的马尔科夫精炼纳什均衡，构造连续有界微分函数V_i（R），i∈（D，E），对于所有的R≥0都满足HJB（hamilton-jacobi-bellman）方程。

政府、企业的HJB方程为

式（16）、（17）均是关于（D_G，Q_G）、（D_E，Q_E）的凹函数，针对式（16）和（17）分别求（D_G，Q_G）、（D_E，Q_E）的偏导数，并令其右端等于0，可得政府、企业的最优策略集为

将式（18）和（19）代入式（16）和（17）中，整理得

根据式（20）和（21）的函数形式可以推测出V^N_G、V^N_E的解是关于L_D、L_Q的二元一次方程，设V^N_G、V^N_E的解分别为

将式（24）和式（25）代入式（18）和式（19），可得政府和企业的最优行为策略。

将政府和企业的最优策略结果，即式（10）、（11）代入至式（3）、（4），并令其等于0，得到稳定状态下的社会数据开放水平L^N*_D及数据开放质量水平L^N*_Q。结合初始条件L_D（0）=L_D≥0、L_Q（0）=L_Q≥0，求解该一阶线性型常微分方程得到社会数据开放水平及质量水平的最优轨迹为

求解式（26）、（27）得到政企合作数据开放的水平L_D（t）及质量水平L_Q（t）的表达式，即式（12）、（13）。

将b₁、b₂、b₃、c₁、c₂、c₃的值代入式（22）、（23）中，即可分别求得政府、企业的最优收益函数，即式（14）、（15）。

命题1得证。

（二）Stackelberg主从博弈（情形S）

在情形S中，政府为激励企业开放数据并提高数据开放的质量水平，作为领导者的政府将为企业分担一定比例的因加大数据开放程度而增加的成本及提高数据开放质量水平而增加成本，即ω_D≠0，0<ω_D<1。企业将根据政府的行为策略和提供的补贴比例来决定自身的最优行为策略，政企双方的博弈过程可以看作是Stackelberg主从博弈，政企双方均以自身的利益最大化为目标。政府和企业的目标函数公式为

命题2：政府和企业在Stackelberg主从博弈中的最优策略分别为

数据开放程度、数据开放质量的最优水平分别为

式（33）、（34）中：U^S、H^S的值分别为

政府、企业的最优收益函数轨迹分别为

证明：为了得到Stackelberg主从博弈的最优解，構造连续有界微分函数V_i（R），i∈（D，E），对于所有的R≥0都满足HJB方程。采用逆向归纳法，首先求解企业的最优策略。

企业的HJB方程为

式（37）是关于（D_E，Q_E）的凹函数，求其关于（D_E，Q_E）的偏导数，并令其右端等于0，可得企业的最优策略集为

政府的HJB方程为

政府将根据企业的行为策略决定自身的行为策略及补贴比例。因此，将式（38）代入式（39）中，再对其求（D_G，Q_G）、（ω_D，ω_Q）的偏导数，并令其右端等于零，得到政府的最优行为策略集及补贴系数集为

将式（38）、（40）、（41）代入式（37）、（39），整理得

根据式（42）、（43）的函数形式可以推测出V^S_G、V^S_E的解是关于L_D、L_Q的二元一次方程，设V^S_G、V^S_E的表达式分别为

整理合并同类项，利用待定系数法求解得

将式（46）、（47）代入式（38）、（40），可得政府和企业的最优行为策略，即式（30）和式（31）。

将政府和企业的最优策略结果，即式（30）、（31）代入式（3）、（4），并令其等于0，得到稳定状态下的社会数据开放水平程度L^S*_D及质量水平L^S*_Q。结合初始条件L_D（0）=L_D≥0、L_Q（0）=L_Q≥0，求解该一阶线性型常微分方程得到社会数据开放程度及质量水平的最优轨迹为

求解式（48）、（49），得政企合作数据开放的水平L_D（t）及质量水平L_Q（t）的表达式，即式（33）、（34）。

将f₁、f₂、f₃、g₁、g₂、g₃的值代入式（44）、（45）中，即可分别求得政府、企业的最优收益函数，即式（35）、（36）。

命题2得证。

（三）协同合作博弈（情形C）

在情形C中，政府和企业不再以自身效益最大化为前提决定自身的最优策略，而是以协同合作的方式，加大整体数据开放及提高其质量水平，以整体效益最大化为前提确定自身的最优策略，在此情况下，得到目标函数为

命题3：政府和企业在协同合作博弈中的最优策略分别为

数据开放程度、数据开放质量的最优水平分别为

式（53）、（54）中：U^C、H^C分别为

总体收益的最优函数轨迹为

证明：为了得到协同合作博弈的最优解，构造连续有界微分函数V（R），且所有的R≥0都满足HJB方程。

式（56）是关于（D_G，Q_G）、（D_E，Q_E）的凹函数，求其关于（D_G，Q_G）、（D_E，Q_E）的偏導数，并令其右端等于0，可得政府、企业的最优策略集为

将（D^C_G，Q^C_G）、（D^C_E，Q^C_E）代入式（56）中得

根据式（59）的函数形式可以推测出V^C的解是关于L_D、L_Q的二元一次方程，设V^C的解为

整理合并同类项，利用待定系数法求解得

将式（61）代入式（57）、（58）得政府和企业的最优策略为

将政府和企业的最优策略结果式（62）、（63）代入式（3）、（4），并令其等于0，得到稳定状态下的社会数据开放水平L^C*_D及数据开放质量水平L^C*_Q。结合初始条件L_D（0）=L_D≥0、L_Q（0）=L_Q≥0，求解该一阶线性型常微分方程得到社会数据开放水平及质量水平的最优轨迹，即式（53）、（54）。

将式（61）代入式（60），得到该模式下政企合作提升数据开放及质量水平的总体收益最优函数，即式（55）。

由协同合作情形下博弈均衡分析可知，政府和企业在加大数据开放程度、提高数据质量水平上付出的努力程度不再受总收益分配比例的影响，即双方不再考虑自身收益的最大化，而是以整体收益最大化为目标判定最优决策。只有在此种情况下，数据开放程度、数据开放质量水平及政企总收益才最高，可实现系统效益最大化，达到帕累托最优。

命题3得证。

四、模型结果比较分析与收益分配机制

（一）模型结果比较

通过比较Nash非合作博弈、Stackelberg主从博弈、协同合作博弈三种模型下的三个命题可以得出如下分析结果。

命题4：比较分析三种博弈模式下政府和企业的最优策略可得

推论1：在Nash非合作博弈与Stackelberg主从博弈中，政府在加大数据开放程度上付出的努力是相同的，同时在提高数据开放质量水平上的努力程度也是相同的；但是当政府在数据开放系统中获得的收益比例为?D的成本，且ω_D≠0，0<ω_D<1。政府在为企业提高数据质量水平上分担比例为ω_Q的成本，且ω_D≠0，0<ω_D<1时，企业在Stackelberg主从博弈情况下的加大数据开放程度与数据开放质量水平的努力程度均高于Nash非合作博弈，且企业在Stackelberg主从博弈情况下增加的加大数据开放程度和提高数据开放质量水平的努力程度等于政府的补贴比例。在协同合作博弈情况下，政府和企业以社会福利最大化为目标，此时政府和企业在加大数据开放程度与提高数据开放质量水平上的努力程度最高，大于Nash非合作博弈和Stackelberg主从博弈两种情况下的努力程度。

命题5：当?

证明：

L^C_D>L^S_D>L^N_D

同理，可得

L^C_Q>L^S_Q>L^N_Q

推论2：对比Nash非合作博弈、Stackelberg主从博弈可知，在政府获得收益的比例为?

命题6：对三种博弈模式下政府和企业的最优收益函数及政企协同合作博弈情况下社会总体的最优收益函数的进行比较分析得

V^S_G>V^N_G

V^S_E>V^N_E

V^C>V^S>V^N（66）

推论3：与Nash非合作博弈相比，在政府为企业承担一定成本的Stackelberg主从博弈的情况下，政府和企业的最优收益均较大；且在协同博弈情况下，社会整体福利效应最高。

（二）合作收益分配机制

由命题6可知，政府与企业在协同合作博弈情形下获得的收益优于分散决策，即Nash非合作博弈情形下的收益达到帕累托最优；但在现实中，若缺少一个权威有效的收益分配机制，该合作状态将很难长久维持。为了使政府和企业在整个博弈过程中均有合作意愿，政企双方之间需要一个权威且具有稳定性的收益分配机制，以此保证在协同合作博弈情形下任一时间点政企双方的瞬时收益高于非合作情形下的收益。

命题7：在政企协同合作情形下，政府和企业在任何时刻Z∈（0， SymboleB@ ），在满足个体理性、整体理性、具有时间一致性条件下的动态瞬时收益分配机制为

第一，合作具有可行性。协同合作成为政企双方最优策略的前提是，在协同合作情况下，政企的总收益大于非合作情形下的總收益。

由命题6可知，V^C>V^S>V^N，故V^C－V^N>0说明政企协同合作具有可行性。

第二，确定政企协同合作下的收益分配机制。政府和企业在协同合作情况下，占系统总收益的收益分配比例由双方各自的谈判能力决定。设政府、企业在协同合作情况下各自提出一个收益分配方案

式（68）中：S_GG、S_GE表示在政府提出的收益分配方案中，政府和企业各自的收益占比，S_EE、S_EG表示在企业提出的收益分配方案中企业和政府各自的收益占比。

一是理想收益分配方案。S⁺=（S⁺（G），S⁺（E）），在此种情况下，政企双方均达到最优收益，此时，

与上述约束条件不符。

二是负理想收益分配方案。S－=（S－（G），S－（E）），在此种情况下，政府和企业均获得最低收益，考虑在三种博弈情形下，Nash非合作博弈下的政企收益均最低，因此可将非合作博弈下的政企收益作为谈判的起点，当其中任何一方在协同合作下的收益低于谈判的起点收益，谈判将结束。

由此，政企的收益分配方案应该在理想收益分配方案与负理想收益分配方案之间，设理想的收益分配方案为S*（V_CG，V_CE），则有如下函数表达式

式（69）中：V^C_G－S－（G）、V^C_E－S－（E）分别表示政府、企业的最终收益与负理想收益之间的差值，它们分别代表政企对最终收益分配方案的满意度，且满意度与此差值成正相关关系，（V^C_G>S－（G）、V^C_E>S－（E））；ηG、ηE分别代表政企双方的谈判能力。

根据库恩-塔克（K-T） 条件，求解上述Nash谈判模型，得到政府和企业最终分配收益为V^C_i=S－（i）+η_i（V_C－∑i=G，ES－（i）），整理得到政府和企业在协同合作情形下获得最合理收益分配方案分别为

其中，

第三，时间具有一致性。上述收益分配机制保证了政企双方在协同合作情况下的收益高于非合作情况下的收益，但是这种个体理性的属性并不能保证随着时间推移，政企仍然选择协同合作，即在Z∈（0， SymboleB@ ）的时间区间内，上述收益分配方案不能使得政企双方满意。因此，政企合作下的收益分配方案需具备时间一致性，设置一个动态收益分配机制A_i（t），（i∈G，E）满足如下表达式

式（71）中：A_i（Z）表示在每个时间点Z∈（0， SymboleB@ ），政企从合作行为中获得的收益；V^C_i（K_C（t））指在合作结束时间点t（考虑无限时间区间），政府或企业获得的终点收益。将政企在不同时间点所获收益以贴现率ρ进行贴现，得到初始时刻政企分到的收益现值V^C_i（K₀）。

对式（71）左右两边求关于t的导数得到动态收益分配函数A_i（t）

将命题1和命题3中的V^N*_G、V^N*_E、V_C分别代入式（65）中得到V^C_i（K_C（t））；再将解得的V^C_i（K_C（t））代入式（66）中得到A_i（t），得到命题7。

五、仿真模拟分析

由命题13可知，政府和企业在Nash非合作博弈、Stackelberg主从博弈、协同合作博弈三种情形下的最优努力程度、最优数据开放程度及质量水平、最优收益均具有差异性，且受多种因素影响，为进一步分析验证上述命题及推论，设μ_DG=μ_DE=γ_QG=λ_QE=2，λ_G=λ_E=φ_G=φ_E=0.6，δ=θ=0.1，W₀=1，v_G=v_E=k_G=k_G=0.5，α=β=0.5，x=0.6，y=10，ρ=0.9。将以上参数的值代入命题13相关公式，使用MATLAB软件进行仿真模拟分析。

图1、2分别表明在三种情形下的数据开放程度及数据开放质量远高于非合作成本分担情形，且成本分担情形下的数据开放程度及数据开放质量均高于非合作博弈的数据开放程度和数据开放质量水平，这说明政府通过共享技术提供补贴等成本分担行为可以有效激励企业加大数据开放程度及提高数据开放质量水平，随着时间的推移，三种情形下的数据开放程度及质量水平增速均放缓并逐渐稳定，符合推论2。

由图3、4可知，政企双方在Stackelberg主从博弈情形下的收益均高于Nash非合作博弈情形下的收益，在同一时间点，政企收益及其总收益均高于非合作情形下的收益，但低于协同合作情形下的收益，说明在?

六、结论与建议

本文在分析数据开放程度及质量水平动态变化的基础上，运用微分博弈方法构建了政企开放数据的三种博弈模型，即Nash非合作博弈模型、Stackelberg主从博弈模型和协同合作博弈模型，探讨了政企最优行为策略、数据开放最优程度和数据开放质量最优水平轨迹、最优收益轨迹，并对上述三种情形下的模型结果进行了对比分析。为了得到在协同合作情形下政企的稳定收益分配，设计了满足时间一致性的收益分配机制，根据微分博弈模型的均衡解得到以下主要结论。

第一，在非合作情形下，政府为企业分担数据开放成本是有效的激励机制，能够显著提升企业在加大数据开放程度、提高数据开放质量的积极性，且企业因成本分担而增加的努力程度等于成本分担比例。

第二，在非合作情形下，政府为企业分担成本，对于提高数据开放程度和数据开放质量水平有较为显著的效果；而在协同合作情形下，社会数据开放水平及数据开放质量水平最高。

第三，政府通过为企业分担成本可以提高政企双方的收益，是帕累托有效的，而在协同合作情形下，政企总收益最高，是帕累托最优的。

第四，通过设计满足时间一致性的合作收益分配机制，可以保障政府和企业维持长久的协同合作状态。

上述模型的研究结果可为社会数据开放提供以下实践指导。

第一，建立科学有效的成本分担机制，为政企合作开放数据提供指导。企业因政府分担成本而增加的努力程度等于成本分担比例，这表明政府为企业分担的成本越多，企业在数据开放中付出的努力越多，政企合作开放高质量数据的效果就越理想，政企获得的收益也就越高。但是，模型结果显示政府自身的努力程度与政府分担成本比例没有相关关系，政府作为领导者可以根据开放数据的类型，针对不同类型的企业制定差异化的成本分担政策，以达到开放数据、满足社会需求的目的。

第二，制定长期稳定的收益分配机制，为政企协同合作提供基础。在协同合作情形下，政企付出努力越大，数据开放程度和开放质量就越高，社会福利效率可达到最优。因此，促进政企协同合作是加大我国数据开放程度及提高质量水平的有效路径。制定公开的收益分配机制可以打破政企之间的信息壁垒，消除政企双方的顾虑，有效维持政企的稳定合作状态，对于我国正处于数字化转型阶段的经济发展具有重要意义。

本文还存在一定的不足，需在未来的研究中考虑以下因素，在数据开放的问题上，不同的地区有各自的发展需求，可考虑根据地区发展需要促进政企重点开放不同类型的数据，以契合地区的差异化发展需要。

参考文献：

[1]中共中央关于坚持和完善中国特色社会主义制度 推进国家治理体系和治理能力现代化若干重大问题的决定[EB/OL]. （2019-11-05）[2021-02-07].http：//www.gov.cn/zhengce/2019-11/05/content_5449023.htm.

[2]樊自甫，程姣姣.新冠肺炎疫情下的数字经济发展机遇与对策研究[J].重庆邮电大学学报（社会科学版），2020（3）：91-101.

[3]郭明军，王建冬，安小米，等.政务数据与社会数据平台化对接的演进历程及政策启示[J].电子政务，2020（3）：32.

[4]复旦大学，国家信息中心数字中国研究院.2020中国地方政府数据开放报告[R].上海：复旦大学，国家信息中心数字中国研究所，2020：4.

[5]张亚楠.论政府数据开放立法的路径及其选擇——以《贵阳市政府数据共享开放条例》为例[J].中国行政管理，2020（2）：38-44.

[6]ATTARD J， ORLANDI F， SCERRI S， et al. A systematic review of open government data initiatives[J]. Government Information Quarterly，2015（4）：399-418.

[7]王娟，王赟芝，曹芬芳.大数据时代政府数据开放共享的博弈分析——基于不完全信息动态模型[J].情报科学，2018（11）：17-22.

[8]毛太田，赵绮雨，朱名勋.基于协同理论的政府开放数据共建共享研究[J].图书馆学研究，2020（11）：28-32.

[9]盛小平，吴红.科学数据开放共享活动中不同利益相关者动力分析[J].图书情报工作，2019（17）：40-50.

[10]沈晶，胡广伟.利益相关者视角下政府数据开放价值生成机制研究[J].情报杂志，2016（12）：92-97.

[11]谭必勇，刘芮.英国政府数据治理体系及其对我国的启示：走向“善治”[J].信息资源管理学报，2020（5）：55-65.

[12]陈朝兵，程申.政府数据开放监管的国际经验与中国路径[J].图书情报工作，2020（12）：49-57.

[13]相丽玲，李彦如，陈梦婕.中外政府数据开放运行机制的实证分析[J].现代情报，2020（1）：134-143.

[14]刘莉，刘文云，刘建，等.英国科研数据管理与共享政策研究[J].情报资料工作，2019（5）：46-53.

[15]吴英慧.美国大数据协同创新及启示[J].情报杂志，2019（4）：168-174.

[16]马续补，吕肖娟，秦春秀，等.政策工具视角下我国公共信息资源开放政策量化分析[J].情报理论与实践，2019（5）：46-50.

[17]吴太轩，朱建海.论政府数据开放的法治化[J].中共福建省委党校（福建行政学院）学报，2020（2）：100-108.

[18]BATES J. The strategic importance of information policy for the contemporary neoliberal state： The case of open government data in the united kingdom[J]. Government Information Quarterly，2014（3）：388-395.

[19]ZUIDERWIJK A， JANSSEN M. Open data policies， their implementation and impact： A framework for comparison[J]. Government Information Quarterly，2014（1）：17-29.

[20]

PALMIRANI M，MARTONI M，GIRARDI D.Open government data beyond transparency[EB/OL].（2014-09-01）[2021-02-07].https：//xueshu.baidu.com/usercenter/paper/show？paperid=b8bf822389d3d0d141e67817379ef9ed&site=xueshu_se.

[21]SADIQ S， INDULSKA M. Open data： Quality over quantity[J]. International Journal of Information Management，2017（3）：150-154.

[22]顾嘉琪，袁莉.基于公众需求的政府数据开放服务质量提升研究[J].情报杂志，2020（6）：196-202.

[23]陈朝兵.超越数据质量：政府数据开放质量的几个理论问题研究[J].情报杂志，2019（9）：185-191.

[24]翟军，陶晨阳，李晓彤.开放政府数据质量评估研究进展及启示[J].图书馆，2018（12）：74-79.

[25]魏益华，陈旭琳，邹晓峰.数据共享、企业策略和政府监督激励——基于演化博弈分析[J].财经科学，2020（4）：107-120.

[26]黄如花，陈闯.美国政府数据开放共享的合作模式[J].图书情报工作，2016（19）：6-14.

[27]徐松鹤，韩传峰.基于微分博弈的流域生态补偿机制研究[J].中国管理科学，2019（8）：199-207.

[28]杜振华.政府数据开放与创新驱动经济增长的关系[J].首都师范大学学报（社会科学版），2020（2）：63-71.

Research on data opening strategy of government-enterprise

cooperation based on differential game

FAN Zifu^1，2， FAN Kexin^1，2

（1. School of Economics and Management， Chongqing University of Posts and Telecommunications，

Chongqing 400065， China;

2. Research Center for Network Synergy Economy， Chongqing University of Posts and Telecommunications，

Chongqing 400065， China）

Abstract：In todays era， data is a key production factor， and its level of openness， circulation， and utilization directly affects the development of the digital economy. However， the level of integration and application in our country is not high at this stage， and the openness and its quality of government and enterprise data still need to be strengthened. Using the differential game approach， considering two factors： data openness and data quality， we construct Nash non-cooperative game， Stackelberg master-slave game， and collaborative game models with government and enterprises as the subjects. According to the Hamilton-Jacobi-Bellman （HJB） equation， we calculate the optimal behavioral strategies， optimal data openness， optimal data quality， and optimal revenue trajectory for government and enterprises under three scenarios. Under time consistency conditions， we explore the revenue distribution mechanism for government-enterprise cooperation. Finally， we conduct simulation analysis of the conclusions under three scenarios. Governments sharing costs with enterprises can promote the openness and quality of social data， achieving a Pareto improvement. In the case of collaborative cooperation， the degree and quality of data openness and the total revenue of government and enterprises are the highest， which can maximize the system benefits. The article established a scientific and effective cost-sharing mechanism to provide guidance for government-enterprise collaboration in opening up data， and developed a long-term stable revenue distribution mechanism to provide a foundation for government-enterprise collaborative collaboration.

Keywords：data openness; data quality level; government-enterprise cooperation; differential game; dynamic income distribution

（編辑：段明琰）