用Geogebra辅助初中物理机械运动图像问题的教学
石俊杰
(乌鲁木齐八一中学 新疆 乌鲁木齐 830000)
人教版第一章“机械运动”初步渗透了时间和空间的概念,教师在教授学生用s-t、v-t等物理图像描述简单的运动时,往往会选择静态的板书或结合教材图片来帮助学生理解运动规律[1],对初中生而言,由于刚刚建立时间和空间的概念,无法将具体的运动情景和物理图像相对应,面对抽象的物理图像,学生脑海里也无法构建起研究对象的运动规律.针对以上这些问题,笔者在实际教学中发现,利用Geogebra辅助机械运动图像问题的讲解,可以克服传统板书的不足,化静为动,激活教材图片[2],解决教学难点.
1 直观化展示机械运动图像的物理意义
认识匀速直线运动是人教版“运动的快慢”这一节的重点,对比教材上图1发现:在每个相同的10 s内,甲车行驶的路程相同,故甲车为匀速直线运动,在s-t图像中可用倾斜的直线表示,在v-t图像中用水平直线表示;乙车在相同时间内,行驶的路程越来越大,则其为变速直线运动,在s-t图像中用越来越陡的曲线表示.为帮助学生建立实际运动情景和物理图像的联系,下面借助Geogebra辅助教学.

图1 人教版“运动的快慢”教科书插图
1.1 直观化展示匀速直线运动s-t图像的物理意义
课件制作核心步骤:
(1)设置滑动条v,范围为0~30;
(2)在绘图区2设置动点E,并将“墨子号”的坐标关联点E;
(3)在绘图区s-t图中设置点H的坐标为[x(E),速度vx(E)].
利用Geogebra做出图1中甲对应的课件如图2所示,绘图区2中的“墨子号”模拟小车匀速直线运动的情景,绘图区实时画出了s-t图像,点击“辅助线”,发现s-t图像中每隔10 s,小车运动的路程均为300 m,学生总结出匀速直线运动的特点:相同时间内的路程相等.同时帮助学生建立起了匀速直线运动的情景与其s-t图像的联系.
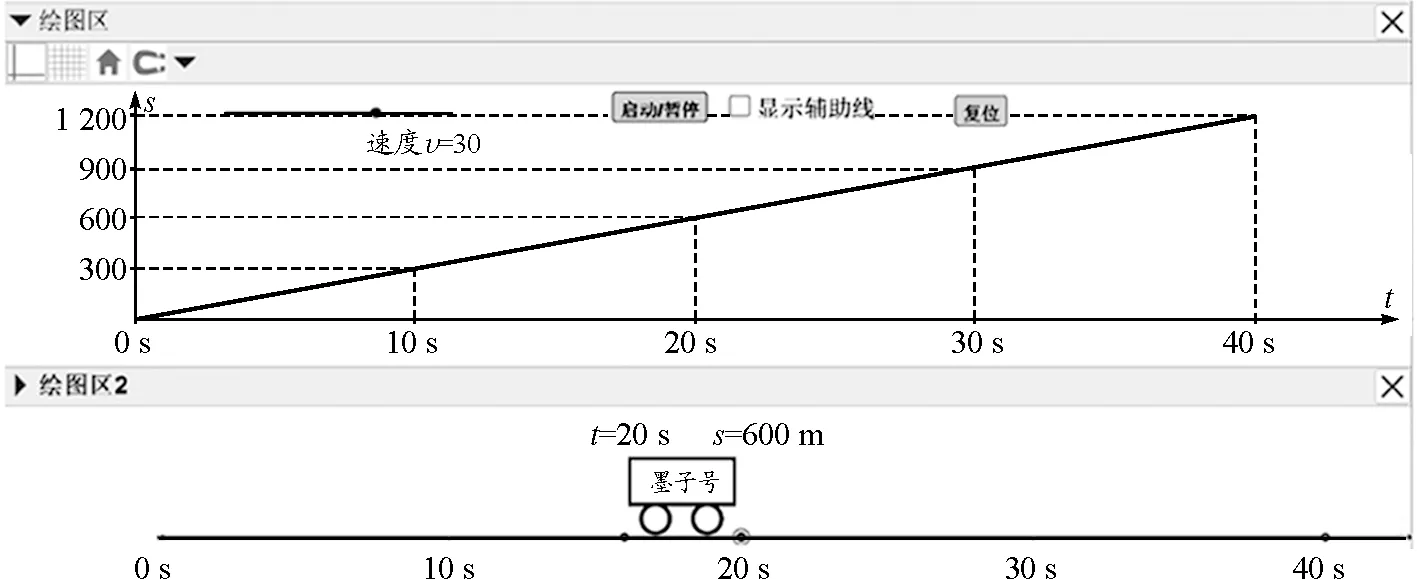
图2 匀速直线运动实际情景与对应的s-t图像
为深入探究s-t图像中的物理意义,改变滑动条速度v的大小,在绘图区中得到不同速度的s-t图像如图3所示,发现图像中直线越倾斜,越靠近s轴,所代表的物体运动的越快,此课件帮助学生建立起匀速直线运动的速度大小和在s-t图像中直线的倾斜程度的联系.

图3 不同速度的匀速直线运动s-t图像
1.2 直观化展示匀速直线运动v-t图像的物理意义
课件制作核心步骤:
(1)设置滑动条v,范围为0~30;
(2)在绘图区2设置动点C,并将“墨子号”图示车的坐标关联点C;
(3)在绘图区v-t图中设置点D的坐标为[x(C),v];
(4)在代数区输入“s=定积分[v,0,x(C)]”;
(5)在绘图区2设置文本text1关联点积分的结果s.
利用Geogebra做出匀速直线运动实际情景对应的v-t图像如图4所示,观察可得:因为匀速直线运动的物体速度大小不变,所以其v-t图像是平行于t轴的一条直线.在40 s内小车通过的路程利用s=vt计算得1 200 m,恰好等于对应图像与t轴围成的面积大小,当物体的速度越大,相等时间内物体走过的路程越大,围成的面积越大.通过此课件帮助学生建立起了匀速直线的路程大小和在v-t图像中与t轴围成的面积的联系.
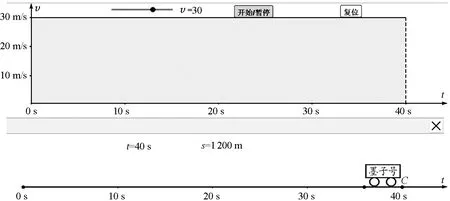
图4 匀速直线运动实际情景与对应的v-t图像
1.3 直观化展示变速直线运动s-t图像的物理意义
课件制作核心步骤:
(1)设置滑动条t,范围为0~40;
(2)在绘图区2设置动点P,并将“墨子号”图示车的坐标关联点P;
(3)在代数区输入“如果(40≥t>30,45(t-30)+750,如果(30≥t>20,30(t-20)+450,如果(20≥t>10,25(t-10)+200,如果[10≥t≥0,20t,0)))]”得到分段函数g(t);
(4)在绘图区中设置动点S的坐标为[x(P),g(x(P))].
利用Geogebra做出图1中乙对应的课件如图5所示,绘图区2中的“墨子号”模拟小车匀变速直线运动的情景,绘图区实时画出了s-t图像,点击“辅助线”,发现s-t图像中每隔10 s,小车运动的路程越来越多,则小车运动的速度越来越快.本情景下的s-t图像不是一条直线,倾斜程度发生了改变,且越来越靠近s轴,与图3的规律一致.

图5 匀变速直线运动实际情景与对应的s-t图像
2 动态化展示机械运动过程
借助Geogebra绘制了匀速直线运动和变速直线运动相关联的s-t和v-t图像,并总结出了图像中对应的物理意义,下面利用总结出的规律分析实际问题.
2.1 动态化展示s-t图像中的追及情景
【例1】运动可缓解紧张情绪,让人感到开心快乐,小明和爸爸从同一地点沿直线步行,他们的路程与时间变化的图像如图6所示,前10 min内,小明看到爸爸______,后10 min内,小明看到爸爸______.(选填“一直前进”“一直后退”“先前进后后退”或“先后退后前进”)
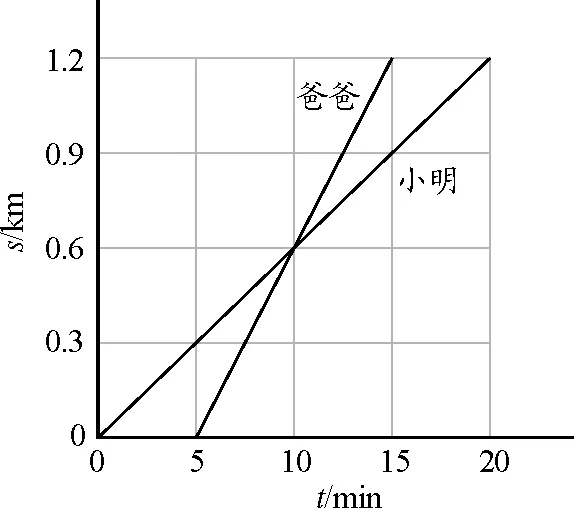
图6 例1题图
课件制作核心步骤:
(1)绘图区2中设置滑动条t,范围为0~20;
(2)绘图区设置动点(0.06t,0) 命名为“小明”;
(3)在代数区输入分段函数“f(t)=如果(0≤t<5,0,5≤t<15,0.12(t-5),15≤t,1.2)”,在绘图区设置动点[f(t),0]命名为“爸爸”;
(4)过两个动点做直线g和h,点A在直线g上,Ah的间距为d,设置文本“d=Ahkm”;
(5)在绘图区设置点“明”的定义为[t,x(小明)],设置点“爸”的定义为[t,x(爸爸)].
利用Geogebra做出例1的课件,如图7所示,在前5 min内,爸爸静止在原地,小明以0.06 km/min匀速步行,爸爸相对小明后退;后5 min爸爸开始步行,依据前面总结的物理意义——s-t图像中描述爸爸运动的直线更靠近s轴,所以爸爸的速度更快,故爸爸和小明间的间距在缩短,则爸爸相对于小明前进,直到第10 min,爸爸在0.6 km处追上小明.
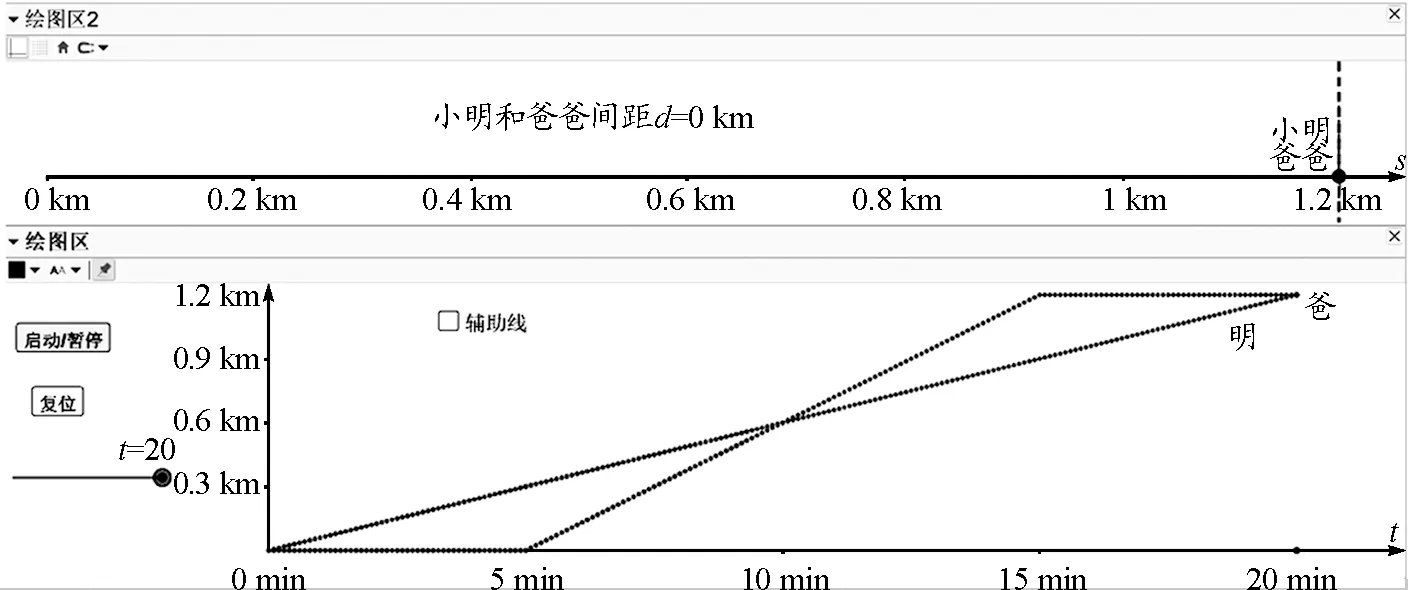
图7 例1 20 min内Geogebra动态化情景
第10~15 min,因为爸爸步行快于小明,故爸爸相对于小明是前进的,且第15 min时相距最远,如图7所示.第15 min以后爸爸停止,小明仍然在步行,逐渐追上爸爸,故此时间段内爸爸相对于小明是后退的,直到第20 min,小明追上爸爸.
2.2 动态化展示v-t图像中的追及情景
【例2】甲、乙两个物体同时从同一地点向东做直线运动,速度与时间关系如图8所示.请观察并解答:
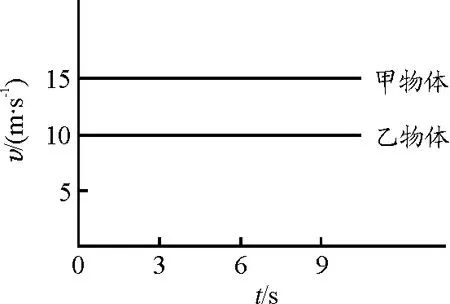
图8 例2题图

图9 例2 9 s内的Geogebra动态化情景
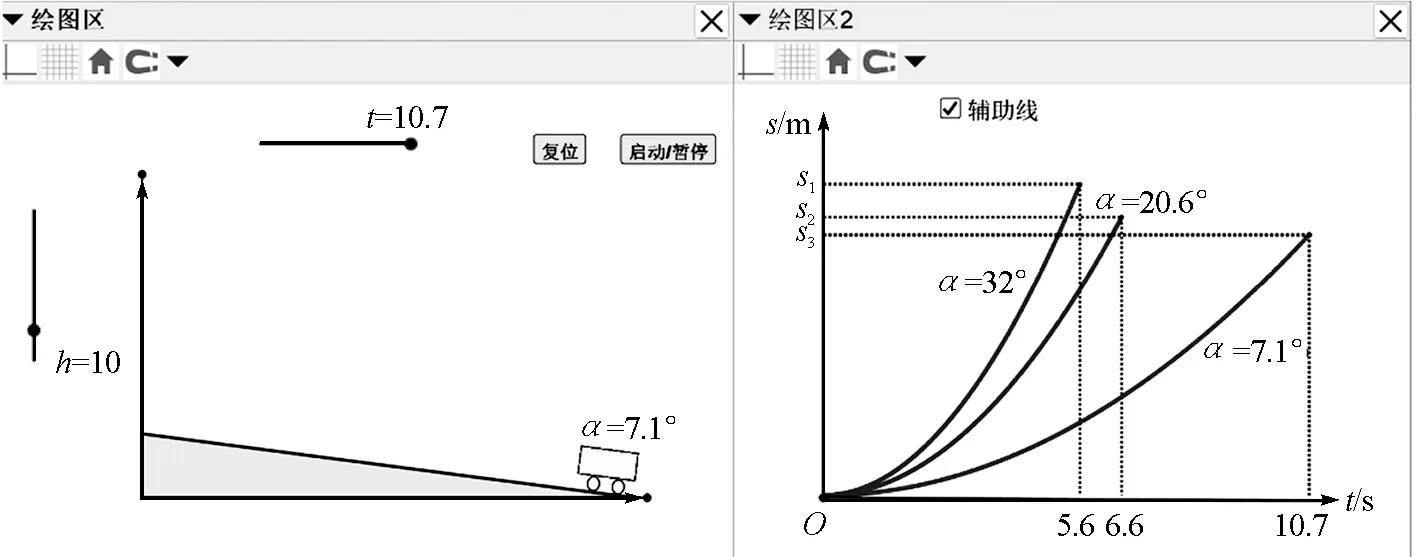
图10 Geogebra可视化探究“测量平均速度”实验不同倾角的情景
(1)以甲为参照物,乙的运动方向是________.
(2)经过6 s甲、乙两物体相距________m
课件制作核心步骤:
(1)绘图区中设置滑动条t,范围为0~9;
(2)绘图区中设置动点甲的定义为(15t,0),动点乙的定义为(10t,0);
(3)过两个动点做直线g和h,点i和点m分别在g、h上,i、m两点的间距为d,设置文本“d=imkm”;
(4)在绘图区2设置点“甲物体”的定义为(t,15),设置点“乙物体”的定义为(t,10);
(5)在绘图区2中设置出多边形q1的定义为 (E,甲物体,乙物体,F);
(6)设置文本“阴影部分的面积”关联q1.
利用Geogebra做出例2的课件如9所示,因为甲物体的速度大于乙物体的速度,故乙相对于甲往东走.在v-t图像中图像与t轴围成的面积代表了物体的路程,甲物体9 s内的路程为矩形GHLK的面积大小,乙物体9 s内的路程为矩形IJLK的面积大小,所以经过6 s后,甲乙两物体的距离为矩形GHJI的面积大小,学生也可以先算出两物体匀速直线运动的速度差为5 m/s,即甲物体每秒比乙物体多走5 m,故9 s内甲、乙相距45 m.经过Geogebra的动态化展示,使得学生数形结合,分析此类问题事半功倍.
3 可视化探究 “测量平均速度”实验
3.1 可视化探究 “测量平均速度”实验合适的斜面的倾角
课件制作核心步骤:(1)绘图区中设置滑动条h,范围为0~50,设置动点B的定义为(0,h).构建斜面t1,设置倾角α;(2)绘图区中设置滑动条t,范围为0~sqrt(32/sin 2α-2/sinα);(3)设置动点C的定义为(x(B) + 10cosα+5t2sinα.cosα,y(B)-5t2sin2α-10sinα),并关联小车示意图;(4)在绘图区2设置动点S的定义为[t,距离(C,B)].
利用Geogebra做出对应人教版“测量平均速度”的课件如10所示,这里调节滑动条h,使得倾角α逐渐变大(本课件中是控制斜面水平边长不变),小车从斜面下滑所用的时间逐渐变短,从t3减小到t1.通过Geogebra课件的可视化演示,帮助学生创建情境,体会实验中斜面的倾角要调整合适,既不能太小,否则实验时间较长,也不能太大,否则时间太短,反应时间占实验时间比重较大,增大了实验误差.
3.2 可视化探究“测量平均速度”实验中大小关系
调整到合适的倾角(α=20.6°)时,Geogebra课件可视化展示了实时追踪小车下滑绘出的s-t图像如图11所示.

图11 Geogebra可视化探究“测量平均速度”实验中速度的大小关系
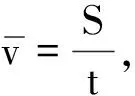
4 结束语
Geogebra是一款优秀的软件,在初中物理“机械运动”这一章教学实践中有很多重要且抽象不易理解的规律和习题,可以借助Geogebra对其复杂规律和物理意义进行直观化展示,对机械运动中追及问题的动态过程进行动态化模拟,增强“测量平均速度”实验探究的可视化,促进学生的深度思考,从而更好地理解物理规律,提高学生的物理学科核心素养[4].
——小明篇——请假
——上课问答

