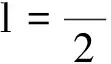巧解微波传输功率*

贺昌辉 朱振波 陈 强 洪 亮 周 乐

(空军预警学院预警技术系 湖北 武汉 430019)

1 引言

微波传输线主要是用来向负载传送微波能量和信息的[1],因此在微波工程中,微波传输功率是一个非常重要的问题.

微波传输线上任意一点的总功率称为传输线的传输功率[2],其物理意义是入射波功率与反射波功率之差.对于均匀无耗传输线而言,因传输线上各点反射系数的大小是相同的,所以各点的传输功率相等,且等于终端负载吸收的功率,又因终端负载的吸收功率与传输线的位置无关,所以可以选取传输线上某些特殊点(如电压腹点或电压节点)来计算传输功率,其表达式为[3]

(1)

式中,|U|max和|U|min为传输线上电压振幅的最大值(电压腹点)和最小值(电压节点),|I|max和|I|min为传输线上电流振幅的最大值(电流腹点)和最小值(电流节点).其中|U|max与|I|max、|U|min与|I|min满足的关系为

(2)

式中,Z0为传输线的特性阻抗.

显然,由式(1)求解微波传输功率,需要计算电压、电流的腹点和节点,易错难解,而且微波传输功率本质上均取决于终端负载ZL,但式(1)中并不含有ZL,所以式(1)是一种间接计算微波传输功率的方法.那么,能否直接用已知条件和ZL来计算传输功率?

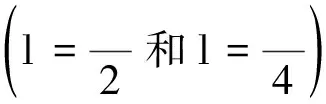
2 结论推导

低频电路是集中参数电路,常常忽略元件连接线的分布参数效应,视为理想导线,电场能量全部集中在电容器中,磁场能量全部集中在电感器中,只有电阻元件消耗电磁能量.电路中沿线电流是同时建立起来的,其大小和相位与空间位置无关,则导线上电压为零.

微波传输线与低频连接线不同,它是一种分布参数电路,也就是沿线处处存在的分布电阻效应、分布电感效应、分布电容效应以及分布电导效应不可忽略,以至于传输线上的电压、电流不仅随时间变化,而且随空间位置变化,因此,传输线上各点电压、电流是不相同的,需要利用电路特点进行计算.

以如图1所示的长为l的微波传输线电路为例,现假设终端为纯电阻负载ZL,C点电压振幅为|U(l)|,下面通过计算负载端D点电压或电流振幅,进而求解电路的传输功率.

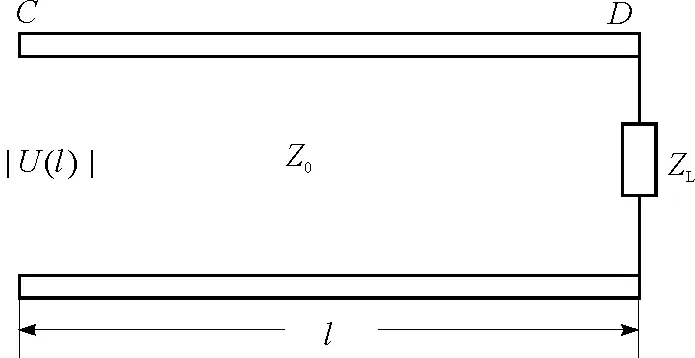
图1 长为l的微波传输线电路

2.1 传输线长度

|U|D=|U|C=|U(l)|

(3)

又知低频电路中终端负载的吸收功率为

(4)

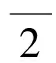
(5)

2.2 传输线长度

|U|C=|U|min=|U(l)|

(6)

由式(2)可得

(7)

若ZL≤Z0,则有则D点为|U|min、|I|max,C点为|U|max、|I|min.

|U|C=|U|max=|U(l)|

(8)

(9)

又知低频电路中终端负载的吸收功率为

(10)

(11)

3 结论应用

【习题】微波传输线电路如图2所示.图中,特性阻抗Z0=75 Ω,R1=150 Ω,R2=37.5 Ω,行波电压幅值|U+|=150 V,试计算负载R1、R2吸收的功率.

图2 微波传输线电路

3.1 常规方法解析

由微波电路的性质可知DC段工作于行波状态,则有|U|C=150 V.

对于CA段

(12)

对于CB段

(13)

3.2 本文方法解析

由式(5)可得CA段负载R1吸收的功率为

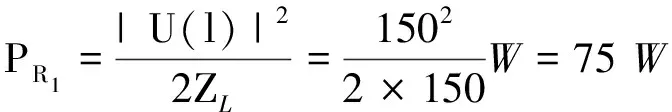
(14)

由式(11)可得CB段负载R2吸收的功率为

(15)

比较上述两种求解微波传输功率的方法,可以看出本文方法解析的优点:

(1)无需根据ZL与Z0的大小关系判断腹点和节点;

(2)无需计算|U|max、|I|max、|U|min与|I|min;

(3)无需计算驻波比ρ或反射系数|Γ|的大小;

(4)让“微波传输功率本质上取决于终端负载ZL”更为直观.

式(5)和式(11)实为巧解微波传输功率的最简单、最有效的方法.

4 结论