关于静电场相关能量的分析*

郭东琴 张 晖 宋冬灵

(信息工程大学基础部 河南 郑州 450001)

在大学物理基础教学中,静电场的能量是静电学中的重要组成部分,教材[1-3]中引入了多种能量概念,如电势能、相互作用能、自能、静电能、电场能等,相应的有各种能量计算公式.日常教学中发现,学生对这些概念的物理意义理解不够透彻,对它们之间的区别和联系容易混淆不清,不能灵活地应用相关能量公式.近年来也有相关方面的教学研究论文[4-6]发表.

本文针对静电场中的各种相关能量概念进行分析,探讨它们之间的区别和内在联系,并结合实例对带电体的静电能进行计算和讨论.

1 相关能量概念解析

1.1 电势能

在静电学中,根据电场力做功与路径无关的特点,引入电势能的概念.电荷在电场中的电势能在数值上等于将此电荷从该点移到零电势能处时电场力所做的功.即

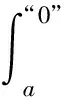
(1)

比如当点电荷q1位于点电荷q2的电场中的a点,且距q2的距离为r时(图1),取无穷远处为电势能零点,那么将q1从当前位置移到无穷远处时电场力做的功

图1 点电荷q1位于点电荷q2的电场中时的电势能

即为q1在a点所具有的电势能

如果是连续带电体位于外电场中,其电势能应将上式改写为

(2)

其中U代表外电场在带电体dq处产生的电势,它是空间位置的函数.

需要注意的是,一个电荷在外电场中的电势能,属于电荷与激发该电场的场源电荷所共有,是一种相互作用的能量.

1.2 相互作用能

对于由若干个带电体组成的系统,若把每一个带电体看作一个不可分割的整体,将各带电体从当前位置移到无限远处静电力做的功称为它们之间的相互作用能,简称互能.互能也等于将各带电体从无限远处移到当前位置时外力克服电场力所做的功.注意任意两个电荷之间的相互作用能属于二者所共有,因此相互作用能仅计算一次,不能重复.两个点电荷之间的相互作用能为

(3)

我们将上式写成对称的形式

(4)

在式(4)中U12是点电荷q2在点电荷q1所在处产生的电势,U21是点电荷q1在点电荷q2所在处产生的电势.

对于多个点电荷所组成的点电荷系,相互作用能为

(5)

式中的Ui是除第i个点电荷以外的其他所有点电荷在第i个点电荷所在处产生的电势.

需要注意,一个点电荷位于另一个点电荷的电场中所具有的电势能正是二者之间的相互作用能,而点电荷系的相互作用能,实际上是该系统所有点电荷具有的电势能之和.需要注意的是,当多个带电体组成带电系统时,假如各带电体所带电荷符号相同,外力做正功,互能为正.当各带电体所带电荷符号不同时,移动各带电体时,外力做功可能为正,也可能为负,总的相互作用能可正可负.

1.3 自能

自能是指一个带电体由无限分散状态聚合起来时所具有的能量,在数值上等于把该带电体上各部分电荷从无限分散的状态聚集起来时外力所做的功.

对于电荷连续分布的带电体,我们可以将带电体上的电荷无限分割为许多小的电荷元dq,而每一个电荷元dq看成点电荷,将电荷元聚合成带电体的过程中外力做的功可通过将式(5)推广计算

(6)

即为连续带电体的自能.该式中的U是除dq以外的其他电荷激发的电势,由于dq在自身所在处产生的电势为一无穷小量,所以上式可以认为是所有电荷在dq处产生的电势.

自能实际上是自身各电荷元之间的相互作用能,只不过从建立带电体自身所需要能量的角度我们把它称为自能.由于同一连续带电体各部分所带电荷符号相同,所以在把这些电荷由无限分散状态构成带电体的过程中外力恒做正功,因此自能恒为正值.

1.4 静电能

把带电系统从无限分散状态聚合到当前位置时外力克服电场力所做的功称为带电系统所具有的静电能.对于由若干个带电体组成的带电系统,我们把建立带电体自身所需要的能量称为自能,把带电体之间的相互作用能称为互能,一个带电系统的总静电能等于各带电体的自能和带电体之间互能的总和.即

(7)

当带电系统的电荷被无限分割,应用式(6)得到的不仅是带电体之间的相互作用能,还包括每个带电体的自能,因此

此时表示的就是整个带电系统的总静电能.当只有一个带电体时,该式给出的是该带电体的自能.

关于带电系统的静电能公式

需注意以下3点:

(1)一个带电系统的自能恒大于零,而互能可以大于零也可以小于零,但自能之和总是大于互能代数和的绝对值,因此一个带电系统的静电能总是正的.

(2)虽然该静电能公式是由点电荷相互作用能公式

导出的,但是点电荷本身的自能发散,无法计算,见本文第2部分应用举例中的讨论.

(8)

式中qi和Ui分别为第i个导体的电荷量和电势.

1.5 电场能

前面给出的静电能公式是与场源电荷相联系的,事实上,电荷的周围存在着电场,外力克服电场力搬运电荷的过程也是电场建立的过程.从这个角度说,静电能储存于电场中,静电能可以用描述电场的特征量电场强度E来表示,又称为电场能.

真空中的静电场能量公式为

(9)

其中E代表体积元dV处的场强,积分遍布在整个电场存在的空间.

对于真空中的静电场来说,电荷和电场都是不随时间变化的,二者同时存在、相伴而生,静电能就是电场能.在变化的电磁场中,电场可以脱离电荷而传播到很远的地方,电磁波携带能量已被证实,电场具有能量是电场物质性的一个表现.

2 应用举例及讨论

【例1】求真空中半径为R,带电荷量为Q的均匀带电球体的静电能.

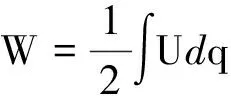
球内距球心为r处的电势为

在距球心为r处选取厚为dr的薄球壳,球壳带电荷量为

带电球体的静电能为

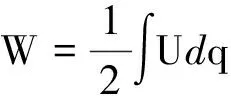
形成半径为r的带电球体,若此时再搬运一半径从r到r+dr的带电球层,此球层带电荷量为dq=ρ4πr2dr,则此过程外力需做功

对整个带电球体的体积积分,所得外力做的总功即是均匀带电球体的静电能W.

由高斯定理可得带电球体内外各点的电场

注意,在应用电场能公式计算静电能时,积分要遍布静电场存在的整个空间.

【例2】真空中有一球形电容器,由半径为R1和R2(R2>R1)的内外两个带电导体球面组成,内球面带电荷量为+Q,外球面带电荷量为-Q,求:(1)该电容器内外球面的自能和相互作用能;(2)系统的静电能.

解：(1)内球面的自能

外球面的自能

内外球面的互能为

其中U12是外球面电荷在内球面所在处产生的电势,U21是内球面电荷在外球面所在处产生的电势.

(2)系统的静电能

解法一：利用W总=W自+W互计算

解法二：利用导体静电能公式(8)计算

注意,这里U1、U2和(1)中U12、U21的区别,这里的U1是内球面电荷所在处的电势

U2是外球面电荷所在处的电势

本题还可以利用电场能公式

进行计算,结果都是一样的.

3 结论

自能是指建立带电体自身所需要的能量,互能指带电体之间的相互作用能量,而一个带电系统的静电能等于各带电体的自能和带电体之间互能的总和.一个电荷在外电场中的电势能,属于电荷与激发该电场的场源电荷之间的相互作用能.对于真空中的静电场来说,静电能等于电场能,当给定电荷分布时,可以从场源电荷和电场这两方面来计算静电能.