爱尔特希点集

郝明皓 整理

匈牙利数学家爱尔特希提出过这样一个问题：在平面内有n（n≥3）个点，其中任意三个点都能构成等腰三角形，这样的点集存在吗？

当n=3 时，若这三个点是等腰三角形的三个顶点，那么符合要求，即n=3时，这样的点集存在。

当n=4 时，有且仅有三种结构符合要求：①任意等腰三角形的三个顶点及它的外心（“外心”是指三角形三边垂直平分线的交点）；②任意菱形（“菱形”是指四边相等的四边形）的四个顶点；③正五边形（“正五边形”是指五条边相等、五个内角相等的五边形）的任意四个顶点。

第①种结构如图1 所示，在△ABC中，AB=AC，D为△ABC的外心。显然DB=DA=DC。从A、B、C、D四点中任取三点构成的三角形均是等腰三角形。

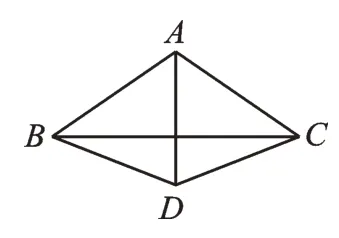
图1

第②种结构如图2 所示，在菱形ABCD中，从A、B、C、D四点中任取三点构成的三角形均是等腰三角形。

图2

第③种结构如图3 所示，在正五边形ABCDE的五个顶点中，任取其中四个顶点，无论取哪四个，它们相对的位置关系均一致，任取三个点构成的三角形均是等腰三角形。

图3

当n=5 时，有且仅有两种结构符合要求：任意正五边形的五个顶点；任意正五边形的四个顶点及其中心（“正多边形的中心”是指其相邻两边垂直平分线的交点）。同学们，你能画出以上两种结构并说明取其中任意三点都能构成等腰三角形吗？当n=6 时，也可以找到满足条件的结构。同学们，你能尝试画出来吗？

当n≥7时，这样的结构便不存在了。

为了纪念提出问题的爱尔特希，人们将具有这样性质的n个点构成的点集称为“爱尔特希点集”。