从“感悟”到“论证”再到“应用”

文／浦梦婷

“轴对称图形”是苏科版数学八年级上册第二章内容。初中阶段几何图形有三大基本变化：平移、旋转、翻折。下面，我们一起来了解本章的具体内容。

一、动手操作，感悟概念

本章的主要学习内容从“轴对称与轴对称图形”出发，理解“轴对称的性质”，从而“设计轴对称图案”，再将轴对称中的知识点转移到“线段与角的轴对称性”和“等腰三角形的轴对称性”。先从生活实际出发，找出生活中的轴对称，再抽象到数学模型，感悟从特殊到一般。

同学们在学习一个新的知识点时，往往先观察，形成初步了解。比如，研究等腰三角形的轴对称性时，很多同学通过观察能够得到“等腰三角形是轴对称图形、顶角平分线是对称轴”以及“等腰三角形两底角相等”，除此以外很难再发现其他结论。但是，通过将等腰三角形两腰进行折叠重合，我们就能够得到“等腰三角形底边上的高线、中线及顶角平分线重合（三线合一）”这个性质。

二、论证推理，明确概念

在动手操作的过程中，同学们对所学知识有了基础的感悟，但这也只能是“猜想”。在数学上，我们称之为“定理”的，都必须要经过严密的论证推理过程。

例1如图1，在等腰三角形ABC中，证明：等腰三角形底边上的高线、中线以及顶角平分线重合（三线合一）。

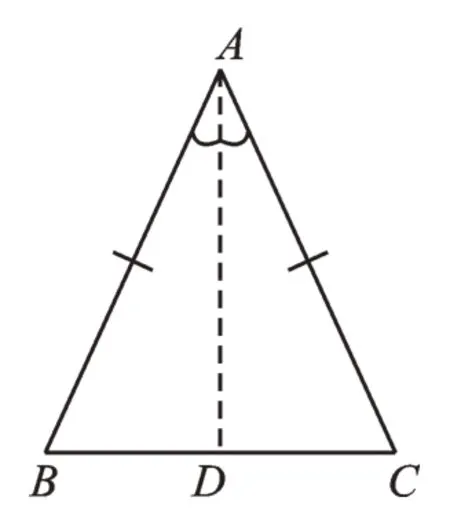
图1

证明：（方法一）作AD平分∠BAC，

∴∠BAD=∠CAD。

由题可得，AB=AC，AD=AD。

在△ABD和△ACD中，

∴△ABD≌△ACD（SAS）。

∴BD=CD，∠ADB=∠ADC=90°。

∴AD是△ABC底边上的高线、中线及顶角平分线。

（方法二）取BC中点D，连接AD。通过“SSS”可证△ABD≌△ACD，从而得到AD⊥BC，AD平分∠BAC。

（方法三）作AD⊥BC，通过“HL”可证Rt△ABD≌Rt△ACD，从而得到AD平分∠BAC，BD=CD。

通过上述论证的过程，我们利用全等三角形的证明，将数学知识串联在一起，增加知识点间的联系，感受到数学的乐趣。

三、应用知识，提升能力

以一道典型题及解法作为根本，我们再深入研究和讨论其他例题。在应用知识的过程中，我们应注重数学规律的揭示、解题策略的优化、合情推理与演绎推理的融合，目的是利用图式启智，探索和发现解决问题的方法。

例2如图2，在△ABC中，AB=AC，D为线段BC上一点，DE⊥AB，DF⊥AC，垂足分别为E、F，且DE=DF，求证：BD=CD。

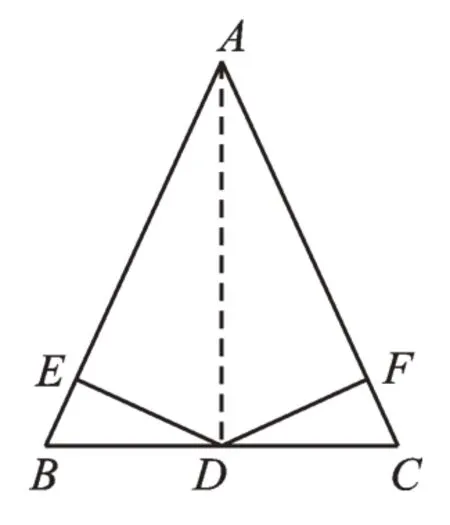
图2

证明：连接AD。

∵DE⊥AB，DF⊥AC，且DE=DF，

∴∠BAD=∠CAD。

又∵AB=AC，

∴BD=CD。

本题将“轴对称图形”中的知识点融合，包含了“角的内部到角两边距离相等的点在角的平分线上”和“等腰三角形三线合一”两个知识点。同学们也可尝试通过全等证明，对比两种方法，选择适合自己的方法。

数学知识层层递进，新老知识联系紧密。因此，我们要学会推理，不断思考，才能提升数学能力。