基于ISSA-LightGBM 的工控入侵检测研究
赵志达, 王华忠
(华东理工大学能源化工过程智能制造教育部重点实验室, 上海 200237)
工控系统(ICS)是国家关键基础设施的重要组成部分[1],在确保炼油、化工、电力、食品、水厂、交通、制药等生产与服务系统稳定运行上起着重要的保障作用[2]。随着信息技术(IT)与工业控制网络的不断融合[3],关键基础设施控制系统已成为互联网的一部分,更容易受到各种网络攻击。ICS 的异常或崩溃可能带来经济损失、环境破坏甚至人员生命损失[4],加强ICS 的网络安全防护十分重要[5]。
工控系统的常见网络攻击包括拒绝服务(DOS)攻击、虚假数据注入(FDI)攻击、侦察攻击、重放攻击等,而入侵检测可以主动监控网络流量和主机等设备,发现并阻止网络攻击[6]。随着人工智能技术的发展,机器学习在入侵检测中的应用越来越广泛[7],然而,工控系统会产生大量的非线性高维数据。传统的机器学习方法,如K 最邻近法(KNN)、支持向量机(SVM)等,虽然算法简单、训练时间短,但是检测准确率相对较低,而且在处理这些工控数据之前需要进行复杂的数据预处理以及人为的特征提取,这需要依靠丰富的经验和大量的实践。卷积神经网络(CNN)、长短期记忆网络(LSTM)等深度学习方法虽然可以避免复杂的数据预处理,且具有较高的准确性,但会消耗大量计算资源,且训练时间长,参数调整困难。
近年来,很多研究人员将机器学习算法应用到入侵检测研究,并取得了一定的成果。黄一鸣等[8]提出了一种基于SVM 的工控入侵检测模型,通过特征增强的方式提高数据集的质量,改善了模型检测精度,但是该方法需要进行复杂的特征变换和数据预处理。陈汉宇等[9]提出了基于统一计算设备架构(CUDA)的并行化策略,将串行SVM并行化,把复杂的计算过程移植到GPU 上,大大提高了模型训练速度,但是该方法成本高、灵活性差。Ling 等[10]提出了一种基于双向简单循环单元的入侵检测模型,使用跳跃连接,通过简单循环单元(SRU)神经网络中优化的双向结构,缓解模型中梯度消失问题,该方法虽然降低了训练时间,但是牺牲了检测效果。刘会鹏等[11]提出了一种基于堆叠LSTM 的入侵检测模型,并采用贝叶斯优化算法对深度学习超参数进行寻优,该方法虽然大大提高了模型检测性能但是却占用大量内存和时间。Narayana等[12]将入侵检测分为两个阶段:第1 阶段,采用平滑L1 正则化增强自编码器的稀疏性,学习特征的稀疏表示;第2 阶段,使用深度神经网络(DNN)对攻击进行检测。由于消除了异常的特征,并通过特征提取降低了特征维数,该模型整体性能优于传统模型。
LightGBM 是Ke 等[13]在2017 年提出的一种改进的梯度提升决策树(GBDT)模型,能够高速准确地处理海量数据,在工业环境中具有良好的应用前景:(1)它支持分类特征的直接输入,在数据预处理阶段无需进行one-hot 编码;(2)它是一种树模型,无需进行归一化操作以处理由于输入变量量纲不同造成的影响;(3)引入EFB 算法进行特征降维,可以省去常规算法要求的特征提取;(4)支持高效的特征并行和数据并行,训练速度快。
基于LightGBM 算法处理工业数据的潜在优势,本文提出了一种基于ISSA-LightGBM 的工控系统入侵检测模型。针对标准麻雀搜索算法的种群多样性少和跳出局部最优解难的问题,提出了一种改进的麻雀搜索算法:(1)引入离散解码策略;(2)使用反向学习策略生成初始种群;(3)麻雀位置更新函数中引入自适应控制步长和收敛因子,使算法具有更优的初始种群和全局搜索能力。将改进后的算法用于LightGBM 入侵检测模型参数的优化,使用密西西比州立大学(MSU)标准工控数据集检测模型的性能,并与其他方法进行比较,验证了该方法在处理大量工业数据时具有检测精度高、训练时间少等优势。
1 LightGBM
1.1 LightGBM 基本原理
LightGBM 是一种GBDT 实现,是为解决传统GBDT 处理大样本高维数据的难题而被提出的。相对于传统的GBDT 算法,LightGBM 不仅保证了准确率,而且训练速度更快[14],内存消耗更低,并且支持分布式并行,可以快速处理海量数据[15],能够有效解决工控入侵检测训练速度慢、占用时间长等问题。LightGBM 的特点和优化算法总结如下。
(1)Leaf-wise 决策树生长策略
多数决策树算法使用的是低效的level-wise的决策树生长策略,同一层的叶子节点不加区分地进行分裂,由于一些叶子节点分裂产生的增益较低,给算法带来了不必要的消耗。与大多数GBDT 算法不同,LightGBM 采用具有深度限制的高效的leafwise 策略,每次层序遍历所有当前叶子节点,仅对增益最大的叶子节点进行分裂,而不是所有叶子节点。因此,经过相同的分裂次数,leaf-wise 策略产生的误差更低,准确率和效率也更高。同时为避免leaf-wise 策略生长出深度比较大的决策树, LightGBM增加了一个最大深度限制,以防止过拟合,能够有效提高模型预测的鲁棒性。level-wise 策略如图1 所示,leaf-wise 策略如图2 所示。

图1 Level-wise 策略Fig.1 Level-wise algorithm

图2 Leaf-wise 策略Fig.2 Leaf-wise algorithm
(2)直方图算法
LightGBM 使用直方图算法对特征数据进行处理,将连续的特征数据离散化为k个整数作为直方图的水平坐标,构造一个以k为宽度的直方图。在遍历数据时,采用直方图累积统计值,然后根据离散的特征统计值确定最佳的特征分割点,因此模型特征只需统计1 次,避免了传统机器学习算法在特征计算时会重复工作的问题。该算法对原始连续特征值进行分箱,并使用这些分箱来构建模型,大大减少了分割点选择的时间消耗和内存消耗,提高了模型的训练和预测效率,特别适用于数据量大、数据维数高的问题。
(3)单边梯度采样(GOSS)算法
LightGBM 引入了GOSS 算法,通过减少训练的数据量来提高训练效率。如果一个训练样本的梯度极小,则表明该样本的训练误差极小,训练已经十分完全,但直接舍弃所有这些梯度较小的样本会降低模型的精度,因此GOSS 算法在减少训练量和保证精度之间进行了平衡。将用于训练的数据根据梯度的大小进行排序,并按一定比例划分为高梯度训练样本和低梯度训练样本,保留所有高梯度样本,对低梯度样本按照一定比例随机采样,舍弃其他低梯度样本。为了防止这样的数据处理对样本分布产生的影响,算法引入放大系数,将保留的低梯度样本乘以放大系数。通过以上这些处理,算法在计算信息增益时会更加关注高梯度也就是训练不足的样本,提高了训练效率。
(4)互斥特征捆绑(EFB)算法
与GOSS 算法不同,EFB 算法通过特征提取的方法提高模型训练的速度。通常的特征提取通过剔除一些无效的特征来降低训练数据的维度,而EFB算法则是通过捆绑互斥的特征来降低训练数据的特征维度。一般情况下,在高维数据空间中,数据是比较稀疏的,在稀疏的特征空间中,有些特征是互斥的,即这些特征不会同时是非零值,通过将这些互斥的特征捆绑在一起,形成一个单一的特征包,大大降低了模型的计算复杂度。
此外,LightGBM 算法支持类别特征的直接输入,不需要进行额外的0 / 1 展开;它支持数据并行和特征并行[16]。这些优化使LightGBM 算法具有更高的效率。
1.2 LightGBM 主要超参数
在机器学习算法中,模型的分类性能好坏与模型超参数的选择有很大的关系,不同超参数组合的模型其表现有很大的差别。LightGBM 模型有较多的超参数,为了获得LightGBM 模型的最优性能,需要对模型参数进行优化。LightGBM 模型的主要超参数如表1 所示。
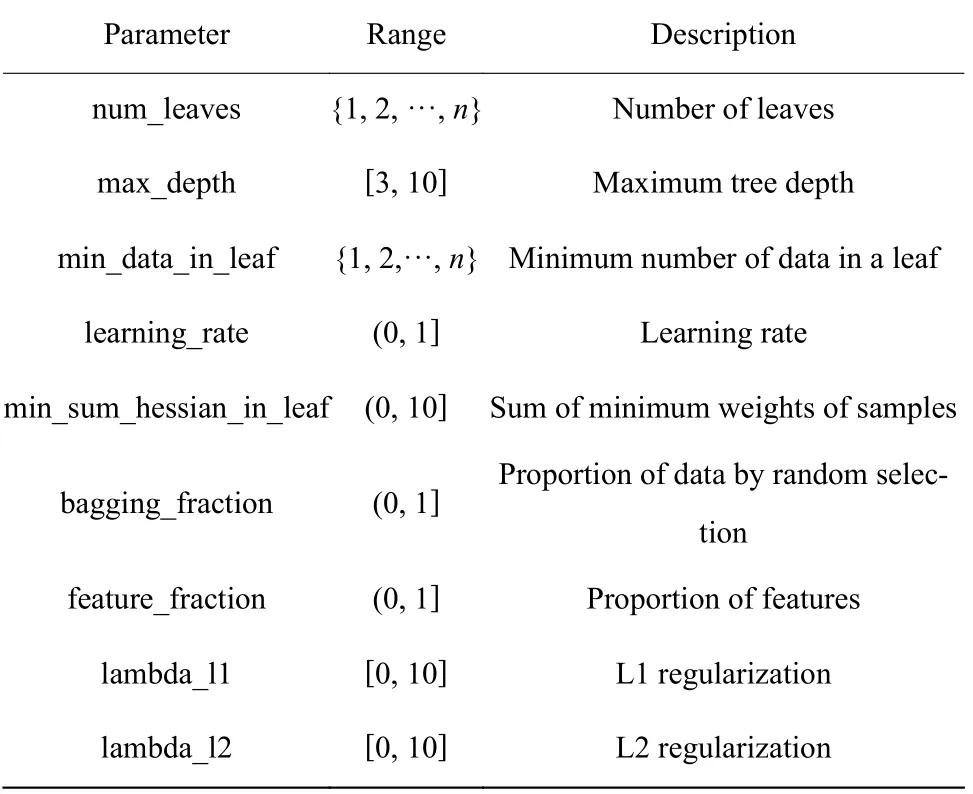
表1 LightGBM 模型的主要超参数Table 1 LightGBM main hyperparameters
不同参数寻优方法得到的最优超参数往往不同,目前常用的有人工搜索法、随机搜索法、网格搜索法等等。人工搜索法需要手动尝试各种可能的参数组合,成本极高且效率低下。网格搜索法采用超参数所有的可能值进行组合,当超参数的变量数和范围增加时,该方法效率会急速下降。随机搜索法使用一系列随机超参数组合,相对于网格搜索算法成本降低,但在测试新的超参数组合时,会忽略前一次组合的效果,导致搜索的效率极低。机器学习模型的超参数优化问题是一种黑盒问题,智能优化算法是解决此类优化问题的十分有效的方法,本文采用改进的麻雀搜索算法进行LightGBM 的超参数优化。
2 改进麻雀搜索算法(ISSA)
2.1 麻雀搜索算法(SSA)
SSA 是Xue 等[17]提出的一种群体智能优化算法,受麻雀的群居智慧启发,参考麻雀的觅食等行为提出的。在SSA 算法中,将麻雀分为生产者、拾荒者和捕食者3 种个体。其中生产者主要为整个种群寻找食物来源,拾荒者则跟随生产者拾取食物,捕食者负责监视觅食的区域。在觅食过程中,不断更新三者位置,完成食物的获取。
在算法中,通过个体模拟麻雀寻找食物。由所有个体组成的种群位置X可由式(1)的矩阵表示:
其中:n表示麻雀种群的数量;d表示待优化变量的维度。
所有个体对应的适应度函数FX可由式(2)的向量表示:
其中FX每一行的函数表示每个个体的适应度值。
2.1.1 生产者位置更新 在SSA 中,适应度较优的生产者在搜索过程中优先觅食,同时,生产者需要为拾荒者寻找食物并引导拾荒者的流动,因此生产者比拾荒者在更广的范围内寻找食物。生产者的位置更新公式如式(3)所示:
其中:t表示迭代次数;j=1,2,...,d;表示第i只适应度较好的麻雀在迭代时的第j维值; α ∈[0,1] ;itermax表示最大迭代次数;R2(R2∈[0,1]) 和ST(ST ∈[0.5, 1.0])分别表示报警值和安全阈值;Q是服从正态分布的随机数,L是 1×d的全1 矩阵。当R2<ST时,意味着周围没有危险,生产者可以广泛搜索食物;当R2≥ST 时,说明麻雀意识到了危险,需飞到安全区域。
2.1.2 拾荒者位置更新 拾荒者的位置更新公式如式(4)所示:
2.1.3 捕食者位置更新 根据算法的设定,捕食者占种群比例的10%~20%。捕食者的位置更新公式如式(5)所示:
2.2 ISSA 算法的实现
2.2.1 离散策略的引入 标准的SSA 算法用来解决连续优化相关问题,不适合用来解决离散优化问题。LightGBM 模型的主要超参数中存在数据类型是整形的,赋予超参数上下界的限制后,其可能的取值是有限的,数据是离散的。在更新麻雀位置的过程中存在参数有小数的问题,为了解决此问题,本文在算法中加入了离散策略。每只麻雀个体是一个1×9 的向量,前6 个变量对应非整型的超参数,采用改进麻雀搜索算法的位置更新方式进行迭代;后3 个变量对应整型的超参数,在麻雀位置更新后,引入离散解码策略,该策略的解码过程如图3 所示。

图3 离散超参数解码过程Fig.3 Discrete hyperparameter decoding process
2.2.2 种群初始化 反向学习策略是群智能优化的一种改进策略,主要思想是根据当前群体产生一个反向群体,比较两个群体的适应度值,择优组成新的群体。针对采取随机生成初始种群个体的标准麻雀搜索算法,引入反向学习策略,有助于提高种群多样性和算法的全局搜索能力。种群初始化步骤如下:
(1)采用随机策略生成n个初始麻雀个体。
(2)生成初始种群的反向种群,反向种群的生成公式如式(6)所示:
其中:pi,j表示初始种群中第i个个体的第j维值;Ubj和 Lbj分别表示第j维变量范围的上下限;Pi,j表示反向种群中第i个个体的第j维值。
(3)对初始种群和反向种群进行整体适应度评估,选取适应度值较优的前n个个体作为算法的初始种群。
2.2.3 改进生产者位置更新方式 标准SSA 算法中,生产者在安全阈值内的位置信息会随着迭代次数的增加逐渐向更小值逼近,忽视了反方向的位置信息,使算法具有很强的局部搜索能力,用于解决极值点在零点的问题时具有很强的优势,而超参数的搜索空间一般都大于零。为了解决上述问题,本文去除了其收敛于零的部分,增加一个正态分布随机数,使超参数上下浮动。同时为了保留原收敛因子的特性,设计了正态分布随机数的方差 σ2,如式(7)所示,其中pop 为种群大小。适应度越好,参数浮动就越小;适应度越差,参数浮动就越大,有助于平衡算法的全局和局部搜索能力。
在SSA 算法中,生产者在安全阈值外位置信息的控制步长为0~1 的数,然而不同超参数的上下界差异过大,采用相同的控制步长会错过一些重要的位置信息。因此,本文引入了自适应步长K,如式(8)所示,每个变量的控制步长由变量的范围决定。
改进后的生产者位置更新如式(9)所示:
3 基于ISSA 优化LightGBM 超参数的入侵检测模型
本文构建了基于ISSA-LightGBM 的工控入侵检测模型。选择LightGBM 模型作为入侵检测的分类模型,采用改进的麻雀搜索算法通过验证集的准确率高低对LightGBM 模型的超参数进行持续的迭代调整,将优化后得到的最优超参数用于构建LightGBM模型,最后将训练集输入给LightGBM 进行模型训练,得到最优分类模型,用以检测工控系统中的攻击。建立基于ISSA-LightGBM 入侵检测模型的流程如图4 所示。

图4 ISSA-LightGBM 入侵检测模型流程图Fig.4 Flow chart of ISSA-LightGBM intrusion detection model
建立基于ISSA-LightGBM 的入侵检测模型具体步骤如下:
(1)数据划分。将原始数据集按照7∶1∶2 的比例随机抽取,划分为训练集、验证集、测试集。训练集用于训练模型;验证集用于在模型超参数的优化过程中评价模型的适应度值;测试集则用于评估最终模型的检测性能。
(2)参数初始化。初始化ISSA 参数(种群大小、迭代次数等),确定LightGBM 待优化的超参数的范围,初始化LightGBM 模型的其他超参数。
(3)初始化种群。采用反向学习策略生成麻雀的初始种群。
(4)位置更新。根据式(9)、式(4)、式(5)更新麻雀种群的位置信息。
(5)离散数据解码。根据离散解码策略对种群位置信息的后3 个变量进行解码。
(6)计算适应度。计算新种群的适应度值,并与上一代进行比较,更新最佳适应度和最佳位置。
(7)判断麻雀种群的最佳适应度值。如果满足终止条件,则停止迭代;否则,返回步骤(4)重新开始迭代。
(8)保存并输出ISSA 的优化结果。最优的麻雀位置信息被用作表格1 中的LightGBM 超参数。
(9)采用最优超参数建立基于LightGBM 的入侵检测模型,并用测试集进行验证,计算各项性能指标并输出。
4 实例分析
4.1 实验环境和数据集
本文实验在Intel(R) Core(TM) i7-4720HQ CPU @2.60 GHz 和Windows10 64 位操作系统的设备上进行,运行环境为python 3.0。为验证本文所提方法的检测效果,使用密西西比州立大学在2014 年提出的天然气管道标准工业数据集[18]。该数据集是从基于Modbus-TCP 通信协议的天然气管道ICS 中收集。数据集包含正常数据样本和7 类攻击数据样本共97 019 条,其中正常数据61 156 条,攻击数据35 863条,具体如表2 所示。
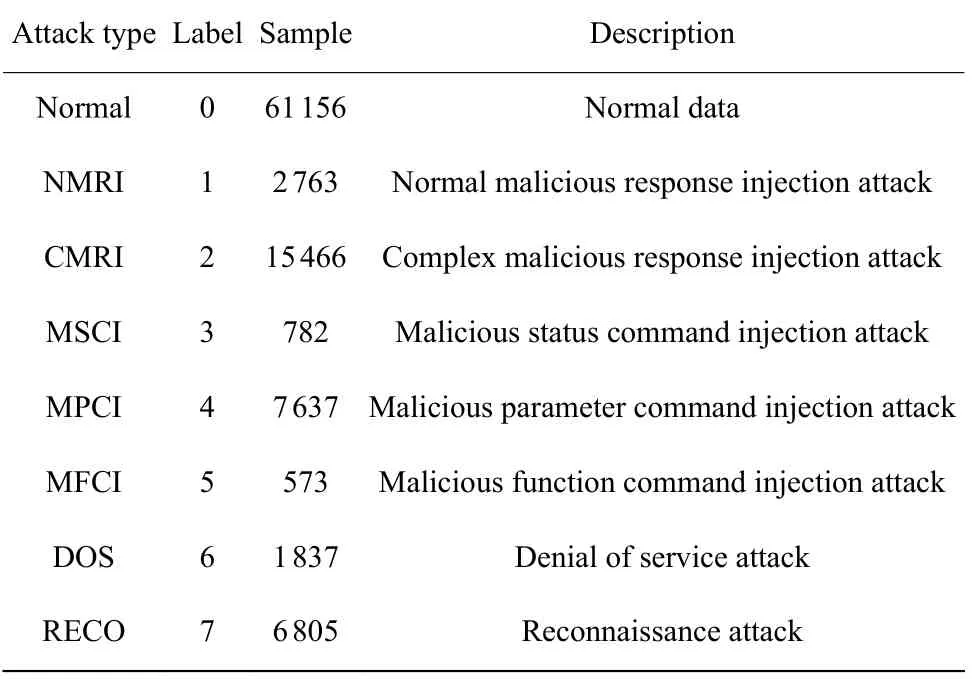
表2 天然气管道数据集的描述[18]Table 2 Description of natural gas pipeline dataset[18]
为了充分验证本文所提算法的检测效果,选择全部原始数据集作为实验数据,且不预先进行任何特征处理或非平衡数据处理。将实验数据按照比例划分为训练集、验证集和测试集,其中训练样本67 910条,约占70%,验证样本9 701 条,约占10%,测试样本19 408 条,约占20%。数据集的每个样本都由26 个特征属性和1 个类别标签组成。
4.2 评价指标
准确率(ACC)可以评估系统的整体性能,误报率(FPR)表示正常流量的错误分类,漏报率(FNR)表示异常流量的错误分类,它们的定义分别如式(10)~(12)所示。本文选择这3 个评价指标来与其他入侵检测模型的性能进行对比。
其中:TP 表示攻击数据的识别数;TN 表示正常数据的识别数;FP 表示正常数据识别为攻击数据的样本数;FN 表示攻击数据识别为正常数据的样本数。
4.3 结果分析
4.3.1 ISSA 性能评估 为了评估ISSA 参数寻优的性能,本文将该算法与基于粒子群算法(PSO)、基于鲸鱼优化算法(WOA)和基于SSA 算法搭建的LightGBM 入侵检测模型进行了比较。由于优化算法每次迭代的每个个体的适应度评价都需要进行建模,为提高效率,在测试优化算法性能的实验中,本文随机均匀地选择10%的数据作为实验数据来测试。在每次实验中,种群大小设置为30,迭代次数30 次。PSO 算法的参数c1=c2=1.5,ω=0.73 ,WOA算法的参数 α 从2 线性递减到0。每种模型独立运行30 次,然后取平均结果,实验结果如表3 所示。迭代过程中各算法的适应度收敛曲线如图5 所示。
从表3 可以看出,总体上LightGBM 模型都具有良好的检测精度,而ISSA 算法搜索到的参数可以更好地优化LightGBM 模型,其入侵检测的准确率为98.92%,误报率为0.67%,漏报率为1.77%,检测精度比其他算法都好,误报率和漏报率也更低,优化所耗费的时间也最少。与SSA-LightGBM 算法相比,ISSA-LightGBM 算法准确率提高0.14%,检测时间减少约25 s。从图5 可以看出,ISSA 算法最优适应度和收敛速度均优于其他算法,虽然在迭代初期,SSA 收敛较快,但由于初始种群的优化,在后续迭代中,ISSA 算法的适应度值均高于其他算法,同时在第8 次迭代时跳出局部最优区域,达到更高的检测精度,这说明本文改进的策略有效提高了SSA 算法跳出局部最优的能力。通过ISSA 算法寻优得到的LightGBM 模型最优超参数如表4 所示。

表4 ISSA-LightGBM 模型的最优超参数Table 4 Optimal hyperparameters of ISSA-LightGBM model
4.3.2 ISSA-LightGBM 入侵检测模型检测效果分析 为了评估本文所提算法在工控入侵检测多分类问题中的性能,采用在表4 中通过ISSA 算法寻优得到的最优超参数建立基于LightGBM 的工控入侵检测模型。选取全部97 019 条数据作为实验数据,得到了该模型的混淆矩阵如图6 所示。

图6 ISSA-LightGBM 模型的混淆矩阵Fig.6 Confusion matrix of ISSA-LightGBM model
从图6 中的混淆矩阵可以看出,本文模型的整体性能十分良好,能够准确有效地识别出绝大多数的攻击。部分正常样本被误报为标签为1、2、4 类型的攻击,同时部分标签为1、2、4 类型的攻击被识别为正常数据,为更准确地验证本文所提模型用于工控系统入侵检测的有效性,实验未对数据集进行任何数据预处理。通过对训练集的分析发现,出现此问题的原因包括两个方面:(1)正常数据中存在一些噪声,导致了正常样本的误报;(2)这几种攻击样本数量较少,样本的不平衡性导致攻击的漏报。尽管如此,本文所提的模型仍表现出了极好的检测性能。
4.3.3 不同机器学习方法比较 为了更全面地评估模型的检测性能,将本文的入侵检测模型(ISSALGB)与KNN、SVM、文献[9]中的CNN 和文献[10]中的SLSTM 共5 种工控入侵检测模型进行对比实验,对比结果如表5 所示。从表5 中可以看出,本文所提算法模型的检测性能最好,准确率高达98.93%,误报率和漏报率低至0.85%、1.45%,远好于传统的机器学习算法,不弱于深度学习算法。模型对近10 万条数据进行训练建模与分类预测,总共耗费时间为6.05 s。在分类准确率上,本文与文献[10]十分接近,但为更准确地验证模型性能,本文全部采用原始数据集,而文献[10]采用SMOTE 算法进行了不平衡数据处理。同时本文用于训练与检测的数据量是文献[10]中数据的近6 倍,是其他模型的近10 倍,虽然文献[10]中的检测时间加上了模型参数优化的时间,但本文模型的检测时间远小于其模型,在检测时间上具有极大的优势。实验结果验证了本文算法能够在保证较高的分类准确率以及较低的误报率、漏报率的同时,拥有较短的训练和预测时间,能够很好地满足工业控制系统的实时性要求。
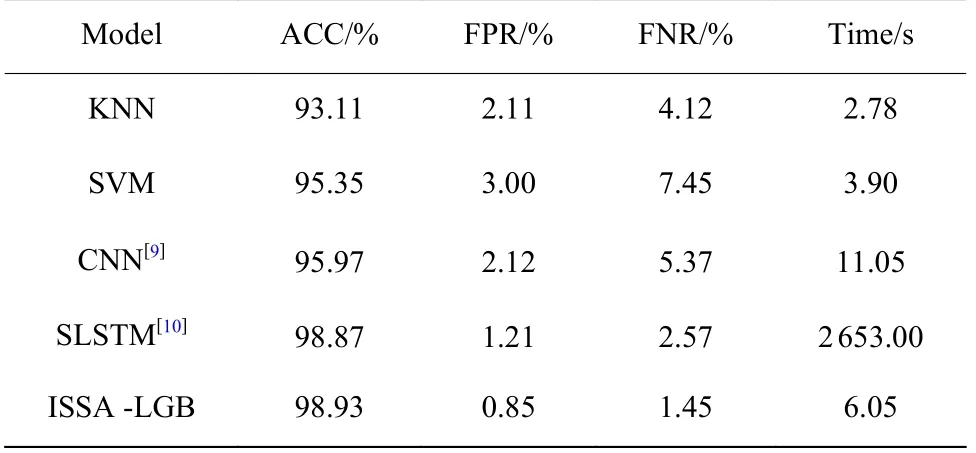
表5 模型性能对比Table 5 Model performance comparison
图7 示出了本文算法模型与对比算法模型对各类攻击数据的检测性能图。从图7 可以看出,各类算法识别正常和攻击数据都有较好的检测效果,但是对NMRI、MSCI、MFCI 的识别效果不佳。本文所建立的模型对所有攻击都有较高的识别率,具有很好的可靠性。对于7 种攻击样本,本文模型的识别准确率均最高,尤其对于来自NMRI、MSCI、MFCI 的攻击,本文模型比其他算法具有极其明显的优势和十分可靠的安全性能。
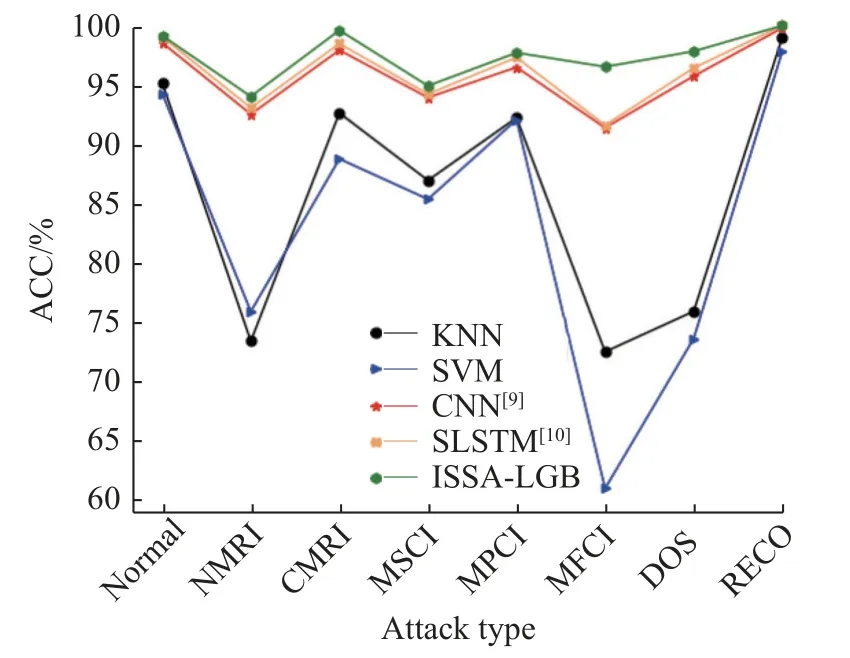
图7 各类攻击检测性能Fig.7 Detection performance of various attacks
5 结束语
本文针对工控网络入侵检测在处理海量数据时高精度和高实时性的要求,提出了一种基于ISSALightGBM 的入侵检测模型。ISSA 引入离散策略保证了参数的合法性,同时改进了初始种群和麻雀的位置更新函数,提高了种群多样性,增强了全局搜索能力,以获取LightGBM 最优超参数。将超参数优化后的ISSA-LightGBM 入侵检测模型与其他基于传统机器学习和基于深度学习的入侵检测算法进行了对比实验,结果表明,本文算法无需复杂的数据预处理,不仅可以更加高效处理海量工控网络数据,而且具有更好的检测性能。

