组合桥面板疲劳荷载后剩余承载力试验研究

武彧， 曾明根， 苏庆田

（同济大学 土木工程学院，上海 200092）

正交异性钢桥面板是由桥面板及纵、横向加劲肋通过焊接而成，因其自重轻、刚度大、整体性强且施工快速等特点成为大跨度桥梁中较常使用的桥面形式［1-2］。但是近些年来，大量工程实例发现正交异性钢桥面板在桥梁服役期存在钢结构疲劳开裂与铺装破坏两类典型的病害，严重影响了桥梁结构的耐久性［3］。

基于此问题，国内外学者对正交异性组合桥面板开展了一系列研究，将传统的带有纵、横向加劲肋的正交异性钢桥面板同混凝土板通过剪力连接件连接起来，利用混凝土板提供一定的面板刚度以期共同抵抗车辆荷载。戴昌源［4］等通过开展相关试验，分析了连接件形式、钢筋直径、混凝土强度等级及钢桥面板加劲肋形式对于组合桥面板负弯矩区混凝土裂缝宽度的影响。邵旭东［5］等提出利用超薄UHPC层代替普通混凝土形成轻型组合桥面板，可较好地解决正交异性钢桥面板铺装层破损与钢结构疲劳开裂的问题。徐晨［6］等对短焊钉超高性能混凝土组合桥面板开展了试验研究，结果表明当短焊钉间距增大时，带有超高性能混凝土的组合桥面板的结构受力更为经济。贺欣怡［7］等提出利用环氧胶代替常规的开孔板或焊钉等剪力连接件实现钢桥面板与混凝土板之间的刚性连接并开展了相关试验，结果表明采用环氧胶粘接的刚性铺装桥面板具有良好的延性与较高的承载力。

与普通混凝土桥相比，组合结构桥梁的活载效应远远大于桥面板恒载效应［8］，车辆荷载的反复作用下混凝土板易发生开裂现象导致结构刚度的降低，严重影响结构的行车舒适性。同时，当混凝土板开裂后，继续承受车辆荷载的反复作用会导致组合桥面板截面刚度的衰减与裂缝的扩张，进而引起结构整体承载能力的下降［9］。目前，学界对于组合桥面板承受循环荷载后的剩余承载力及其刚度衰减规律的研究还不充分，过往的研究大多聚焦于组合桥面板的疲劳强度或正交异性钢桥面板连接细节处的疲劳性能分析［10-15］，关于疲劳后剩余承载力的试验研究则集中于重载铁路预应力混凝土梁及组合梁［16-17］，针对组合桥面板疲劳荷载作用下的承载力衰减研究相对较少。

为分析研究正交异性组合桥面板在疲劳荷载作用下的受力性能退化，本文通过一块足尺正交异性组合桥面板试件的静载破坏试验与一块足尺正交异性组合桥面板试件的疲劳后静载试验，测试其在集中荷载作用下桥面板试件的应变、挠度、裂缝发展，得到其极限承载力与破坏形态，验证了车辆荷载反复作用后的结构承载力退化情况。最后，在现有规范的基础上，从钢筋混凝土黏结滑移理论出发，考虑疲劳荷载对钢筋混凝土之间黏结效应的削弱作用和纤维桥接作用，提出考虑钢筋与混凝土之间疲劳后黏结应力的平均裂缝间距计算公式和组合桥面板极限承载力简化计算方法，为分析了解组合桥面板开裂后行为提供参考。

1 试验研究

1.1 背景工程

背景工程为一大跨连续组合钢箱梁桥，跨径布置为104m+165m+104m，其断面布置如图1所示。正交异性组合桥面板宽度为54.02m～61.70m，桥面板采用闭口U形加劲肋，口宽360mm，每间隔4m设置一道横隔板；混凝土桥面板采用现浇钢筋混凝土结构，钢梁与混凝土桥面板之间通过剪力钉连接，剪力钉直径为16mm，高度为90mm，纵横向间距360mm；主梁钢箱截面在墩顶截面梁高7.0m，跨中截面梁高4.5m，梁高按二次抛物线规律变化。钢材为Q345qD，混凝土为C60低收缩纤维混凝土。

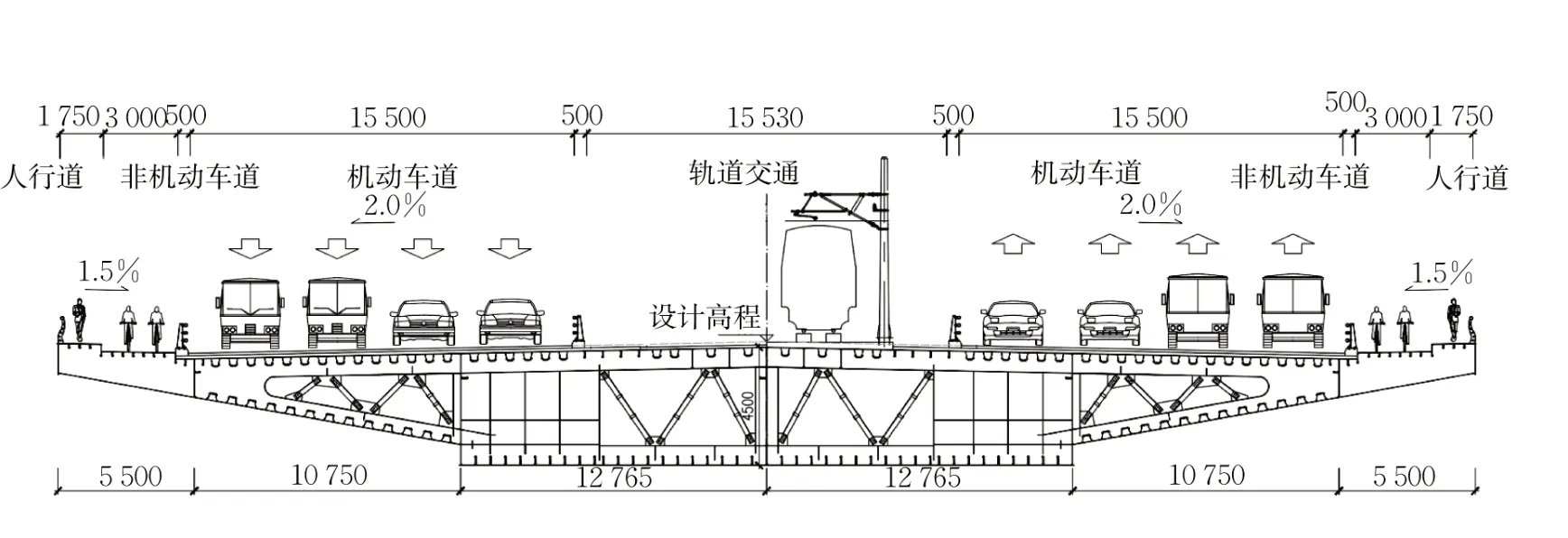
图1 断面布置图（单位：mm）Fig.1 Plan and cross section of prototype bridge structure（Unit: mm）

1.2 试件设计

设计制作2个正交异性组合桥面板试件，一个无疲劳荷载作用，一个有疲劳荷载作用，两个试件分别命名为SCB-S与SCB-F，两个试件的混凝土板依据背景工程选择120mm厚钢纤维混凝土，试件尺寸横向取两个U肋宽度（1 440mm），纵向包括两个完整横隔板间距（8.8m）。试件横隔板高为450mm，U肋高度为300mm，顶板厚度为12mm，U肋厚度为8mm。混凝土板内纵横向钢筋直径16mm，间距均为120mm，采用HRB400带肋钢筋。试件设计如图2所示。

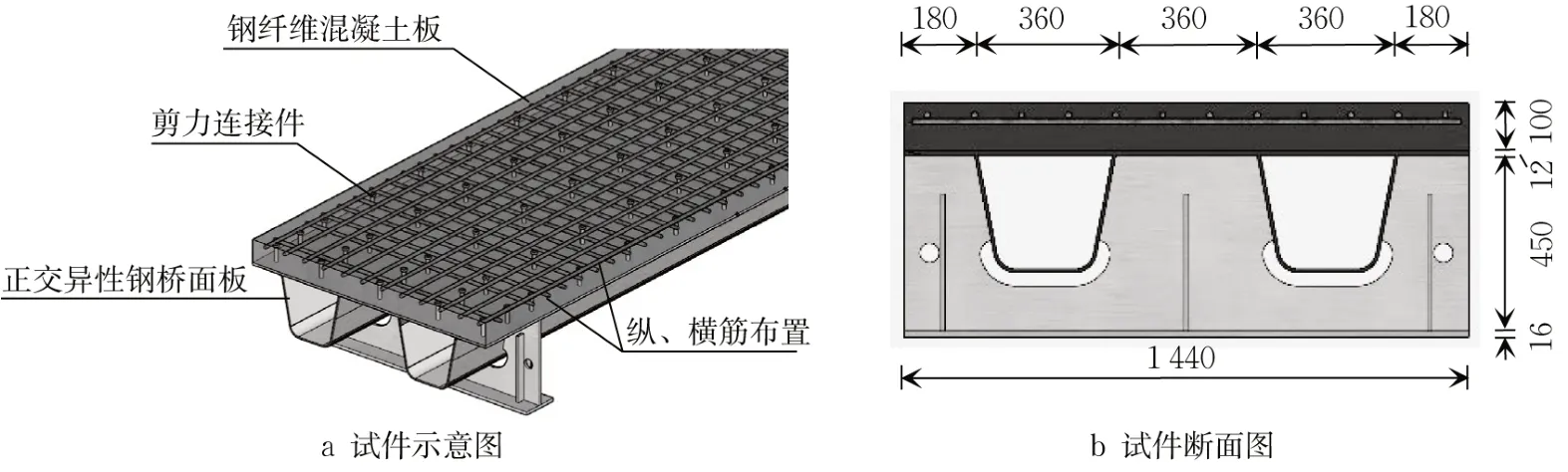
图2 试件设计图（单位：mm）Fig.2 Schematic Diagram of Specimen（Unit： mm）

1.3 加载方案

试验加载方式及测点布置如图3～图4所示，其中静力加载采用在两侧跨中位置设置电液伺服作动器的方式施加竖向力，疲劳荷载加载则在一侧跨中布置脉动疲劳加载试验系统施加往复荷载。在试件SCB-S和SCB-F两侧跨中加载点及中支点截面均布置位移计以测试试验过程中试件的变形；在试件SCB-S和SCB-F的两侧跨中与中支点截面的纵向钢筋、混凝土板上表面、钢梁顶板下表面、U肋1/2高度处及U肋底板下表面布置应变计以测量试件的应变。

图3 试件加载示意（单位：mm）Fig.3 Loading setup（Unit： mm）

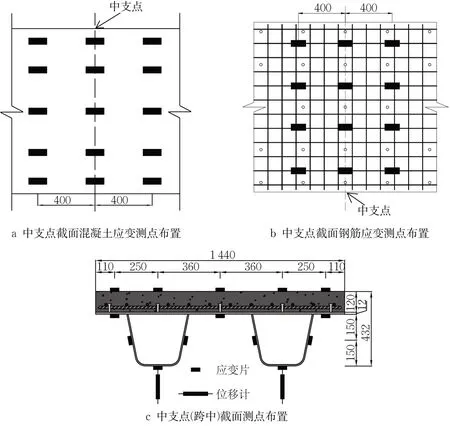
图4 试件测点布置（单位：mm）Fig.4 Arrangement of measuring points of specimen (Unit: mm)

试件SCB-S仅经历静力破坏一个试验阶段，加载分为力控制加载与位移控制加载两部分，力控制加载分为预加载与正式加载，预加载是为了排除加载设备与采集设备可能出现的故障，正式加载首先以每级25kN加载至中支点负弯矩区混凝土层开裂，之后以每级100kN加载至钢桥面板屈服，最后转为位移控制加载直至结构最终破坏。

试件SCB-F经历疲劳循环加载与静力破坏两个阶段，疲劳加载采用疲劳试验机进行200万次等幅荷载的疲劳试验，总共分为4个加载阶段，每个加载阶段均进行50万次荷载循环，加载频率为4Hz。疲劳加载的荷载上、下限及荷载幅值如表1所示。静力破坏加载方式与试件SCB-S相同。

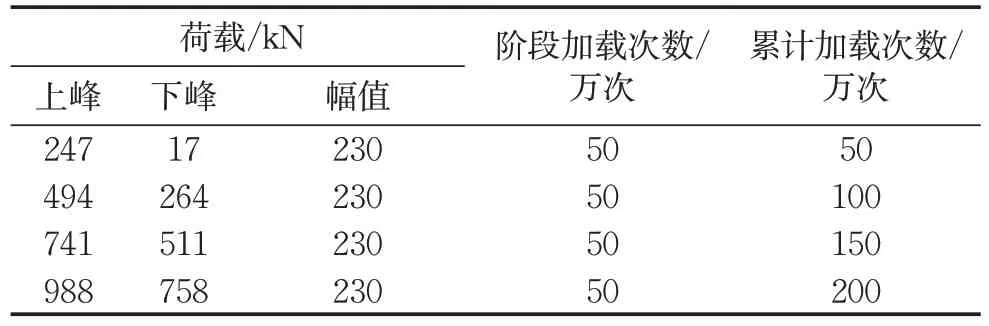
表1 疲劳加载历程Tab.1 Load level for each loading period

1.4 材料性能

测试了与试验试件相关的主要受力材料的力学性能。其中厚度为8mm和12mm厚钢板的屈服强度分别为411MPa和370MPa，抗拉强度分别为554MPa和511MPa；直径16mm的钢筋屈服强度为549MPa，抗拉强度为664MPa。边长150mm的标准立方体钢纤维混凝土试块养护28d抗压强度为85MPa。

2 试验结果

2.1 荷载-位移曲线

试件SCB-S跨中加载点截面的荷载-位移曲线如图5 a 所示，试件经历了钢结构屈服前的线弹性受力阶段和屈服后的非线性受力阶段。在线弹性阶段，试件的荷载-位移曲线基本呈现出线性的特征，两侧加载点跨中位移随荷载的增大而线性增大；在该阶段末，当荷载达到0.68Pu时，中支点U肋下缘开始屈服，试件进入非线性阶段。随着荷载的增加，曲线斜率逐渐变小；当荷载达到0.72Pu时，两侧跨中加载点截面U肋下缘受拉屈服；继续加载，中支点U肋下缘受压屈服面积增大，直至中支点处U肋发生屈曲变形，试件SCB-S的屈曲荷载为0.96Pu；之后，随着中支点处U肋屈曲变形严重，结构到达承载力峰值Pu（为2 019kN）。此时荷载-位移曲线已近乎水平，试件跨中加载点处挠度不断增大，荷载的变化幅度较小；在非线性阶段末，构件两侧跨中加载点处混凝土压溃，中支点截面上层钢筋受拉屈服，结构无法继续承载，此时对应的剩余荷载值为0.86Pu，试件破坏时的跨中截面挠度为133.24mm。

在完成试件SCB-F的疲劳加载后进行静力破坏试验，图5 b为试件SCB-F经历静力加载时跨中加载点截面的荷载-位移曲线。在加载的初期，试件跨中位移随荷载的增大而线性增大；当荷载达到0.67Pu时，中支点截面U肋下缘受压屈服，曲线出现明显偏转；之后随着荷载等级的继续增大，荷载-位移曲线的斜率逐渐减小，表明随着荷载的增加与中支点截面U肋受压屈服的发展，试件逐渐表现出非线性受力特征；当荷载达到0.97Pu时，中支点截面U肋出现屈曲变形；不同于试件SCB-S，试件SCB-F到达屈曲荷载后即变形严重，结构迅速到达承载力峰值Pu（为1 784kN），荷载-位移曲线趋近水平；继续加载直至构件两侧跨中加载点处混凝土压溃，中支点截面上层钢筋受拉屈服，结构无法继续承载，此时对应的剩余荷载值为0.98Pu，试件破坏时的跨中截面挠度为91.85mm。

试件SCB-F的破坏形态如图6所示。

图6 试件破坏形态Fig.6 Failure modes of specimen

汇总两试件试验的主要荷载如表2所示。

表2 试件测试结果Tab.2 Bridge deck test results

由图5荷载-位移曲线可以看出，试件SCB-S与SCB-F在线弹性阶段，即荷载水平达到约0.67Pu时，切线刚度分别为115.25kN·mm-1和100.6kN·mm-1，试件经历疲劳荷载后刚度下降约12.7%。结合表中数据，试件SCB-F的中支点U肋下缘屈服荷载、跨中U肋下缘屈服荷载、中支点U肋屈曲荷载和极限荷载均比试件SCB-S的小，说明桥面板受到反复荷载作用后其受力性能产生明显退化，本文试验试件经历疲劳荷载作用后的极限承载力下降了11.6%。然而，对比图5两试件的荷载-位移曲线，发现试件SCB-S的中支点U肋下缘屈服荷载、跨中U肋下缘屈服荷载、中支点U肋屈曲荷载与极限荷载的比值分别为0.68、0.72和0.96，试件SCB-S的上述3个数值分别是0.67、0.72和0.97，且两试件的剩余荷载也非常接近，这说明受反复荷载作用桥面板的受力性能发生退化，且这种退化对试件的典型受力特性基本上产生同比例的影响。

2.2 裂缝特征

随着荷载等级的逐步提升，试件中支点负弯矩区域混凝土产生裂缝，且裂缝的宽度随荷载的增大而不断扩张。在试件开裂后，每隔一定荷载等级进行一次裂缝观测，详细记录裂缝的分布情况并测量裂缝的最大宽度。

试件SCB-S的开裂荷载为350kN，初始裂缝宽度为0.04mm；之后，随着荷载的不断增大，试件中支点两侧区域开始对称出现裂缝。当荷载达到中支点U肋屈服荷载（1 383kN）时，中支点区域裂缝数量不再有明显增加，仅裂缝长度与宽度在既有裂缝的基础上继续发展，此时最大裂缝宽度为0.14mm；当荷载增大到1 600kN时，最大裂缝宽度达到0.20mm。

试件SCB-F在经历先期的疲劳荷载加载后，中支点负弯矩区域混凝土板上表面的裂缝已经初步形成，裂缝主要分布于中支点靠近加载侧约400mm范围内，且经历疲劳加载时最大裂缝宽度维持在0.09mm左右，卸载后所有裂缝均闭合；在静力破坏加载过程中，随着荷载的逐步增大，试件中支点区域混凝土裂缝数量、长度均出现明显变化，裂缝宽度亦随着荷载的增大而逐渐增大，当荷载达到1 600kN时，最大裂缝宽度达到0.21mm。

试件的裂缝分布对比如图7所示，试件SCB-S的裂缝较为集中的分布在中支点截面左右约400mm范围内；试件SCB-F的裂缝数量更多，贯通板宽的主裂缝数量亦更多，且裂缝分布范围更广，主要分布于中支点截面两侧约500mm范围内，且在局部区域除纵向裂缝外还有横向裂缝的产生，说明高周等幅疲劳荷载加速了混凝土板的裂缝发展。

在主要的裂缝上选取多个测点，测量混凝土板裂缝宽度，得到两试件不同荷载等级下的最大裂缝宽度，如图8所示。从图8可以看出，在相同荷载等级下试件SCB-F的裂缝宽度始终大于试件SCBS，二者的最大裂缝宽度发展趋势大致相似，仅数值上相差0.01～0.02mm，这是因为在疲劳荷载作用下，混凝土裂缝经历了多次的闭合与张开，使得混凝土板的裂缝宽度随疲劳荷载循环次数的增加而略有增大。

图8 试件最大裂缝宽度曲线FIg.8 Maximum Crack Width at Different Load

3 混凝土平均裂缝间距计算方法

对于钢纤维混凝土结构，当负弯矩区混凝土板开裂时，裂缝处的混凝土并未完全退出工作，钢纤维桥接作用使得开裂处混凝土仍有残余抗拉强度，这种残余强度减小了钢筋与混凝土之间所需的传递长度从而减少了平均裂缝间距。然而，对于疲劳荷载作用的混凝土板，高周疲劳荷载会导致混凝土与钢筋之间黏结强度降低，造成钢筋与混凝土之间传递长度的增大进而引起平均裂缝间距的增大。因此，对于疲劳荷载作用后的高性能混凝土组合桥面板，其平均裂缝间距的计算不仅需要考虑钢纤维的作用还要考虑高周等幅疲劳荷载导致的钢筋黏结强度降低。

3.1 基本假定

依据规范GB 20010—2010［18］提供的平均裂缝间距计算公式，参考钢筋混凝土黏结滑移理论，推导疲劳荷载作用后的钢纤维混凝土组合桥面板负弯矩区平均裂缝间距计算公式，并做出如下假设：

（1） 钢纤维混凝土桥面板出现裂缝后，并未直接退出工作，该处界面混凝土仍旧以残余抗拉强度值参与受力。

（2） 裂缝出现前瞬间，受拉区混凝土应力呈矩形分布，应力值为混凝土抗拉强度值。

（3） 裂缝出现前后，截面中和轴位置的移动忽略不计，即裂缝出现前后钢桥面板承受弯矩不变。

（4） 对于承受疲劳荷载的构件，考虑疲劳荷载对于钢筋与混凝土之间黏结效应的削弱作用。

（5） 黏结传递长度lcr范围内钢筋的应力差与钢纤维混凝土应力差均由钢筋与混凝土之间的考虑疲劳荷载削弱作用的平均黏结强度τm承担。

3.2 等效残余抗拉强度值

依据欧洲材料与结构联合会关于纤维混凝土的标准［19］（RILEM TC 162-TDF）中有关钢纤维混凝土受拉开裂时的截面应力（如图9所示）可得：虽然桥面板负弯矩区混凝土抗拉强度随裂缝的出现而降低，但总体上钢纤维混凝土仍旧保持着一定的开裂后残余强度与变形能力。为确定钢纤维混凝土的抗拉残余强度，引入文献［20］中的纤维增强混凝土轴拉本构模型（如图10所示），该模型的关键即是A点对应的应变值εtp、B点坐标（αεtp，γ1ft）与C点对应的最终应变值εu的确定。根据文献［20］与Marco［21］等对于纤维增强混凝土的研究，结合实验分析与工程实例，取εtp为ft/Ec，其中ft为混凝土轴拉强度值，Ec为混凝土弹性模量；α为13.0；γ1为0.3；εu可取为2%。

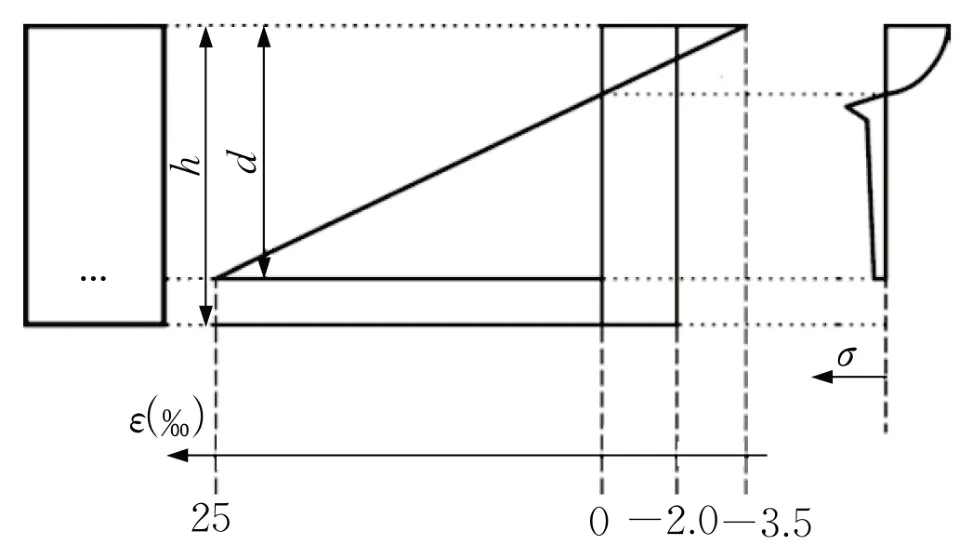
图9 钢纤维混凝土开裂截面应力分布Fig.9 Stress distribution of cracked section of steel fiber reinforced concrete

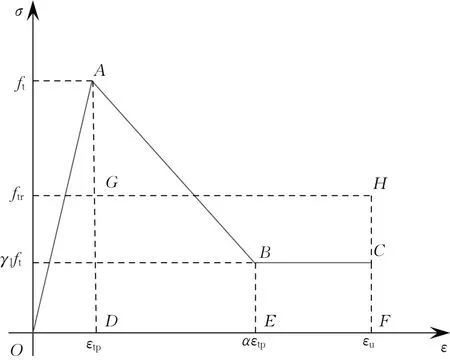
图10 纤维增强混凝土轴拉本构曲线Fig.10 Axial tension constitutive curve of fiber reinforced concrete

从A点到B点再到最后的C点，钢纤维混凝土始终保持着较高的残余抗拉强度，C点以后对应的强度由于应变过大可忽略不计，仅考虑从混凝土抗拉峰值点开始的ABC两段。依据能量等效原理进一步简化钢纤维混凝土残余抗拉强度值的计算，引入等效残余抗拉强度值ftr一概念，通过模型曲线包络面积SDABCF=SGHFD求出混凝土开裂后的等效抗拉强度值，可得ftr=0.53ft。

3.3 计算公式

对于钢筋混凝土构件而言，一旦混凝土开裂，原本受拉的混凝土就会向开裂截面两侧收缩，此时混凝土与钢筋之间即产生相对滑移与黏结应力。当离开开裂截面的距离达到最小裂缝间距lcr时，二者之间的相对滑移与黏结应力消失，结构易出现第二条裂缝。

基于此，正交异性组合桥面板负弯矩区混凝土最小裂缝间距lcr可通过平衡条件求得，取ab段为隔离体（裂缝间距为lcr），该隔离体受力情况如图11所示。

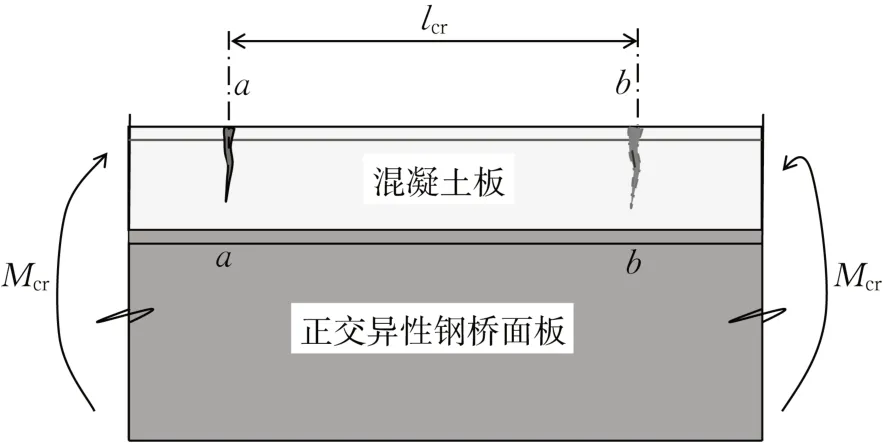
图11 组合桥面板局部受力情况Fig.11 Local stress situation of composite bridge deck

第一条裂缝处的钢筋应力为σs1，即将出现第二条裂缝处的钢筋应力为σs2。两边的不平衡力由黏结力平衡，因此，由平衡条件可得

其中：Δσs为不平衡应力差；μ为纵向受拉钢筋截面总周长。若截面a与截面b承担的弯矩均为Mcr，则可以得到截面a中的钢筋应力为

其中：Mc，re为开裂截面混凝土残余强度提供的弯矩值；Ms为正交异性钢桥面板承受弯矩值；ηa为截面a钢筋内力臂系数；h0为截面有效高度；As为纵向受拉钢筋截面面积。在截面b处，Mcr可视为由三部分构成，一部分为混凝土承担的Mc，一部分为正交异性钢桥面板承担的Ms，另一部分为钢筋承担的Mr。

其中，ηb为截面b钢筋内力臂系数，根据假设（3），由于截面开裂前后中性轴位置改变忽略不计，因此可以忽略a截面与b截面上钢筋所承担的内力臂间的差异，近似认为截面a与截面b钢筋内力臂系数ηa=ηb=η。根据前述式（1）可得

对式（5）进行简化处理，计算可得

如此，由式（6）可得疲劳荷载作用后混凝土桥面板理论最小裂缝间距计算公式为

根据混凝土黏结滑移理论，理论上的最小裂缝间距为lcr，最大裂缝间距为2lcr，则平均裂缝间距为lm=1.5lcr。

最终，疲劳荷载作用后的正交异性钢混组合桥面板平均裂缝间距宽度表达式即为

式中：hc、bc分别为混凝土桥面板的高度及宽度；ηc为截面混凝土内力臂系数。

3.4 钢筋黏结强度

上世纪80年代，为明确钢筋与混凝土之间的黏结机理及其黏结强度的变化规律，国内外学者针对不同锚固形式的钢筋混凝土构件开展了一系列拉拔试验［22-24］，试验结果表明，影响变形钢筋黏结性能的主要因素为混凝土强度、保护层厚度、配箍率与锚固长度，并给出了变形钢筋的平均黏结强度τm建议计算公式如下：

其中：c为钢筋保护层厚度，d为钢筋直径；lab为钢筋基本锚固长度；ft为混凝土抗拉强度值。

八十年代末，章文纲和程铁生［25］针对钢纤维混凝土开展了一系列拉拔试验，研究表明在混凝土中掺入钢纤维并不改变黏结强度与混凝土之间的黏结性能，即在相对锚长、相对保护层厚度等条件相同的情况下，钢纤维混凝土与变形钢筋之间的黏结强度仍旧同钢纤维混凝土的抗拉强度成正比。并建议钢筋与钢纤维混凝土的锚固强度计算公式仍采用与式（10）相同的形式，仅用钢纤维混凝土抗拉强度值代替常规混凝土抗拉强度值，即

式中：dsv，Ssc为箍筋的直径和间距；frt为钢纤维混凝土抗拉强度值。

为分析钢筋混凝土结构在高周疲劳荷载作用下的黏结锚固性能，Rehm和Eligehausen［26］对锚固钢筋的疲劳性能作了详细的研究，结果表明：如果在疲劳荷载作用下黏结疲劳破坏没有发生，随后持续增加荷载，黏结-滑移曲线仍旧会沿着静载情况下的曲线变化规律发展。因此，当钢筋混凝土构件经历的峰值荷载小于其疲劳强度对应的荷载值时，先前施加的疲劳荷载仅影响其正常使用情况下的黏结性能而不会对极限承载力时的黏结性能造成影响，即对于接近破坏时的钢筋混凝土构件而言，其黏结强度仅与疲劳荷载作用后的混凝土剩余抗拉强度值相关。

基于此，对于承受疲劳荷载作用后的混凝土构件，可仍旧使用式（11）提供的钢筋与钢纤维混凝土间的平均黏结强度τm，仅对其中混凝土抗拉强度值进行修正，用混凝土疲劳后剩余强度ftmax代替常规混凝土抗拉强度ft，ftmax=γpft，γp为疲劳荷载作用下的混凝土疲劳强度折减系数。此时，式（11）变为

我国《混凝土结构设计规范》（GB50010-2010）［18］规定，疲劳强度折减系数可根据疲劳应力比值确定，其中为截面同一纤维上的混凝土最大及最小应力，此规定同前苏联《铁路、公路和城市桥涵设计规程》（CHИΠ2/05/03/84）［27］中规定的混凝土疲劳强度折减系数γp=0.6εb相似，εb为考虑不同疲劳应力比ρ的调整系数。

铁科院的姚明初［28］则根据混凝土在等幅与变幅重复应力作用下的力学性能试验研究提出混凝土在等幅或变幅重复应力作用下会出现相应的疲劳残余变形增量Δε，并以此推导得出相对应的混凝土强度折减系数γp=fmax/ft估算公式为

其中：N为混凝土的疲劳循环次数。可以看到，该计算公式不仅引入了应力水平比值σmin/ft，还考虑了混凝土经受重复应力的循环次数。

而日本、欧洲与美国的规范［29-31］及相关文献则以混凝土受疲劳荷载时的应力变程fcr=σmax-σmin表达混凝土的疲劳强度，其中σmax与σmin分别对应混凝土重复应力的上限和下限。此时，疲劳荷载作用下的混凝土强度折减系数γp=fmax/ft仅与应力水平比值σmin/ft相关。

3.5 结果对比

将各设计规范和文献中提出的混凝土疲劳强度折减系数带入式（12）求得对应的考虑疲劳荷载影响的钢筋黏结强度，进而得出承受疲劳荷载作用后的钢纤维混凝土组合桥面板的平均裂缝间距，并将其与试验结果相比较，具体结果见表3。

表3 平均裂缝间距试验值与计算值比较Tab.3 Comparison of experimental and calculated average crack spacing

由上表可得，采用不同设计规范或文献提供的混凝土疲劳折减系数带入本文建议的平均裂缝间距的计算公式均具有较好的精度，试件平均裂缝间距试验值同计算值吻合程度较好，二者比值在0.85～1.10之间，变异系数为0.092，计算结果可信。当然， 为保证建议计算公式有更好的使用范围和计算精度， 应在后续研究中扩大试验试件数量， 以扩大样本空间。

4 极限承载力计算方法

基于前述分析可得，对于疲劳荷载作用的钢纤维混凝土组合桥面板，当计算其极限承载力时，不仅需要考虑钢纤维混凝土材料的抗拉贡献，还需考虑疲劳荷载作用后的混凝土抗拉强度衰减问题。因此，本文提出一种考虑疲劳荷载作用和纤维桥接作用的组合桥面板极限承载力计算方法，并作出如下假设：

（1）钢桥面板同混凝土板之间连接良好，不考虑二者之间的相对纵向滑移。

（2）考虑疲劳荷载作用，对混凝土轴拉强度值进行修正，用混凝土疲劳后剩余强度ftmax代替常规混凝土抗拉强度ft，ftmax=γpft。

（3）钢纤维混凝土板开裂后并未退出工作，受拉区混凝土以残余抗拉强度值参与受力，结合3.2节分析残余抗拉强度值为ftr=0.53ftmax，ftmax为混凝土疲劳后剩余轴拉强度值。

（4）受压区钢板均匀受压，受拉区钢板匀受拉，且均达到其屈服强度fy。

（5）受拉区钢筋均匀受拉，且均达到其屈服强度fst。

5 结论

通过开展静力破坏试验与疲劳荷载加载后的静力破坏试验研究了疲劳荷载作用后的正交异性组合桥面板受力性能退化的情况，得到了极限承载力、裂缝分布情况及最终破坏形态，具体研究结论如下：

（1）静力破坏试件SCB-S的破坏形态为受弯破坏，当达到极限承载状态时，中支点截面U肋屈曲变形严重，上表面混凝土开裂明显，两侧跨中加载点处混凝土压溃，整体结构出现明显的塑性变形；疲劳加载后的试件SCB-F静力破坏试验破坏形态同试件SCB-S一致，亦表现为受弯破坏。

（2）本文的试验结果表明在疲劳荷载作用下，正交异性组合桥面板的受力性能退化11.6%，而且对组合桥面板的典型受力特性产生同比例的退化影响；试件SCB-F在线弹性阶段的刚度较试件SCB-S下降了约12.7%。

（3）疲劳荷载会加速混凝土桥面板的裂缝发展，经历疲劳荷载作用后的试件SCB-F裂缝分布范围较静力破坏试件SCB-S扩大了25%，相同荷载等级下，试件SCB-F的最大裂缝宽度始终大于试件SCB-S。

（4）在考虑经历疲劳荷载作用后组合桥面板受拉区混凝土剩余抗拉强度的基础上，根据钢筋混凝土黏结滑移理论建立了适用于疲劳荷载作用后的钢纤维混凝土组合桥面板平均裂缝间距计算公式，并通过试验结果进行了验证；结果表明该平均裂缝间距计算公式计算值同本文试验值吻合程度良好，并以此提出一种考虑疲劳荷载作用和纤维桥接作用的组合桥面板极限承载力简化计算方法，可为实际工程的应用提供理论参考。

作者贡献声明：

武彧：试验设计、数据分析及论文写作与修改；

曾明根：论文选题、指导论文修改；

苏庆田：论文选题、指导试验设计及论文修改。