考虑软逻辑的鲁棒项目调度优化
张立辉, 李怡菲, 邹 鑫, 曹蔷楠,3
(1.华北电力大学 经济与管理学院,北京 102206; 2.华北电力大学 经济管理系,河北 保定 071003; 3.内蒙古大学 创业学院,内蒙古 呼和浩特 010021)
0 引言
国内外已经对确定性环境下的项目调度问题进行了多年研究,然而,由于当前市场环境的迅速变化,复杂工程项目(如“一带一路”跨国项目、PPP项目等)所面临的风险和不确定性日益严峻,例如活动工期估计不准确、资源供应不及时、机器故障、恶劣天气影响以及设计变更等。这些不可控因素会扰乱项目活动的有序执行,造成组织和协调上的混乱,从而导致工期延误、成本增加等问题。例如,港珠澳大桥由于周边区民质疑其环境评估,延期长达9个月,损失88亿元;长沙霞凝110kV变配套线路工程执行过程中由于设计经常修改,导致工期延误长达6个月。因此,在不确定环境下,制定一个具有强抗干扰能力的基准进度计划非常有必要。
鲁棒性项目调度通过充分考虑不确定性因素的干扰从而制定抗干扰能力强的进度计划和灵活的应对策略,已经成为近年来国内外学者研究的热点问题。鲁棒性项目调度的优化目标分为质量鲁棒性和解的鲁棒性[1],质量鲁棒性是指调度方案对于目标函数的稳定性,解的鲁棒性是指调度方案在执行过程中按照计划执行的稳定性。在质量鲁棒性方面,大多数研究主要集中在度量方式上,其中项目工期和按时完工率[2]是最为常用的目标函数。何立华和孔云霄[3]提出了一个基于活动延期风险和前继活动数量的质量鲁棒性衡量指标,并通过算例验证了该指标的优越性。在解的鲁棒性方面,CHTOUROU和HAOUARI[4]考虑项目活动间的优先关系约束,将自由时差优先分配给紧后活动数量较多的活动。HERROELEN和LEUS[5]以活动实际与计划开始时间的偏差损失成本最小为目标,利用活动总时差提升进度计划的鲁棒性。何正文等[6]用活动的时间缓冲与其权重系数的乘积之和衡量解的鲁棒性,将时间缓冲分配给工期变化性较高的活动。一些研究也集中于质量鲁棒性和解的鲁棒性的权衡优化。Al-FAWZAN和HAOUARI[7]以自由时差之和表示解鲁棒性,构建工期最短和鲁棒性最大的双目标模型,并采用禁忌搜索算法进行求解。HOOGEVEEN[8]采用即时完工率最大和活动开始时间偏差最小两个目标,通过赋权加和的方式将其转化为一个复合函数求解。张静文等[9]从时差效用函数新视角衡量调度方案的鲁棒性,建立工期-鲁棒性双目标资源约束型鲁棒调度优化模型,并设计了快速非分配性排序多目标遗传算法。
软逻辑是指项目工序可采用与预先施工逻辑顺序不同的方式进行施工的一种进度计划组织方式。例如,“地基挖掘1→地基挖掘2→…→地基挖掘I”,上述活动在工艺和技术上相互独立,可以互换施工顺序,也可以选择同时进行。TAMIMI和DIEKMANN[10]首次在CPM中提出软逻辑概念,并将其应用于突发事件引起的网络计划图更新。El-SERSY[11]进一步将软逻辑分为三个子类型:SOFT,OR和EXCLUSIVE-OR,同样应用于网络计划图的更新。FAN[12]在项目延迟分析中提出了一种基于软逻辑的项目调度更新算法,使工期延长的计算更加合理、准确。在调度优化方面,WANG[13]探究了在活动工期不确定条件下,三种软逻辑对项目工期的影响,并提出估算项目总工期的PROSOFT模型。FAN等[14]提出了一种基于软逻辑的重复性项目优化模型的遗传算法,旨在帮助管理者根据不同的工作效率和逻辑顺序寻求最低的总成本。张立辉等[15]综合考虑软逻辑对项目总工期和成本的影响,建立了多模式时间-费用权衡问題模型。综上所述,软逻辑已被应用于项目工期和费用的优化研究,但尚未发现将软逻辑应用于不确定环境下项目鲁棒调度优化的研究。
基于以上事实,本文将探究软逻辑对项目鲁棒调度的影响,建立基于软逻辑的双目标鲁棒项目调度优化模型,并设计e-约束算法对其进行求解,以求进一步提升项目鲁棒性,从而为项目管理者提供相关决策支持。
1 考虑软逻辑的双目标鲁棒项目调度优化模型
1.1 软逻辑类型及其对项目调度方案的影响
(1)软逻辑类型
EI-SERSY[11]将活动间的软逻辑关系分为三种类型:OR,EXCLUSIVE-OR和SOFT,如图1所示,其中(a)表示活动A和B的软逻辑关系为“OR”型,即活动A和B可以同时进行,但不可以互换施工顺序;(b)表示活动A和B的软逻辑关系为“EXCLUSIVE-OR”型,即活动A和B可以互换施工顺序,但不可以同时进行;(c)表示活动A和B的软逻辑关系为“SOFT”型,即活动A和B间的关系同时具备“OR”型和“EXCLUSIVE-OR”型的性质,既可以同时进行,也可以互换施工顺序。
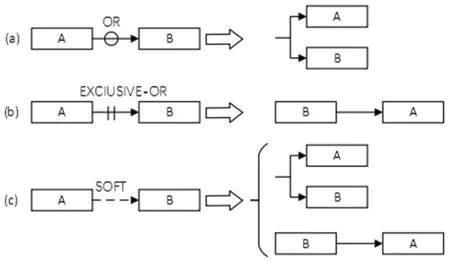
图1 软逻辑类型
(2)软逻辑对项目工期和解鲁棒性的影响
在项目调度方案中,关键路线的长度直接决定了项目的总工期,不确定环境下每个活动的自由时差由于能起到缓冲的作用而与项目的解鲁棒性直接相关。软逻辑为项目调度提供了更大的灵活性,一方面通过合理地调整软逻辑的顺序,可以改变项目调度的关键路线从而影响总工期;另一方面软逻辑顺序的变化,可以改变活动间的优先关系,进而对活动的自由时差的计算产生影响,并最终影响解鲁棒性的大小。考虑如图2所示的一个活动间存在软逻辑的简单项目,当不考虑软逻辑时,即采用固定逻辑施工时,项目的关键路线为1-3-5,总工期为12天,活动4有6个单位的自由时差,如图2(a)所示;当考虑软逻辑时,活动3和5同时进行,活动2和4互换施工顺序,项目的关键路线变为4-2-5,总工期缩短为11天,此时活动1和3都有2个单位的自由时差,如图2(b)所示。
(3)软逻辑对紧后活动数量的影响
鲁棒性指标是鲁棒项目调度研究中较为关键的环节,大多数研究在建立鲁棒性指标时都会考虑紧后活动数量这一要素。因此,有必要探究软逻辑对紧后活动数量的影响。
当活动i及其紧后活动j之间的顺序发生变化,活动i,j以及j的潜在紧前活动的紧后活动数量都会发生变化。以图3所示网络计划图为例,分析三种类型软逻辑对紧后活动数量的具体影响,作为构建鲁棒优化模型的基础:
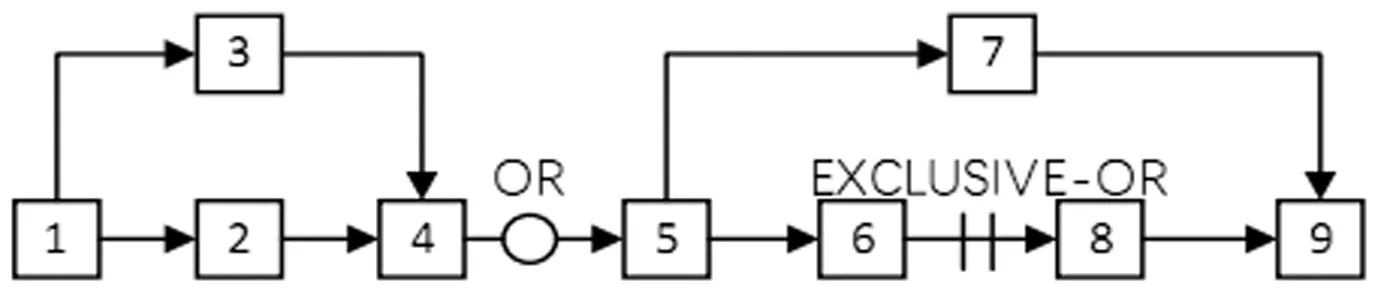
图3 某工程项目网络计划图
1)OR型软逻辑对紧后活动数量的影响。如图4所示,活动i的紧后活动数量变为(NDSi-1+PSi),其中NDSi为活动i的初始紧后活动数量,PSi为活动i潜在的紧后活动数量;若活动j存在潜在紧前活动,则该潜在紧前活动的紧后活动数量变为(NDSpprej+1),其中pprej为活动j的潜在紧前活动,NDSpprej为活动j潜在紧前活动的初始紧后活动数量。
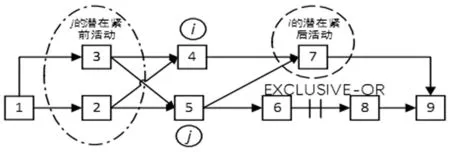
图4 OR软逻辑顺序变化后的网络计划图
2)EXCLUSIVE-OR型软逻辑对紧后活动数量的影响。如图5所示,活动i的紧后活动数量变为(NDSi-1+PSi);活动j增加一个紧后活动i,若活动i存在潜在的紧后活动,此时活动j将失去对该活动的实际约束,则活动j的紧后活动数量变为(NDSj+1-PSi);若活动j存在潜在紧前活动,则该潜在紧前活动增加一个紧后活动j,但此时该活动也会失去对活动i的实际约束,因此,该活动的紧后活动数量可视为不变。
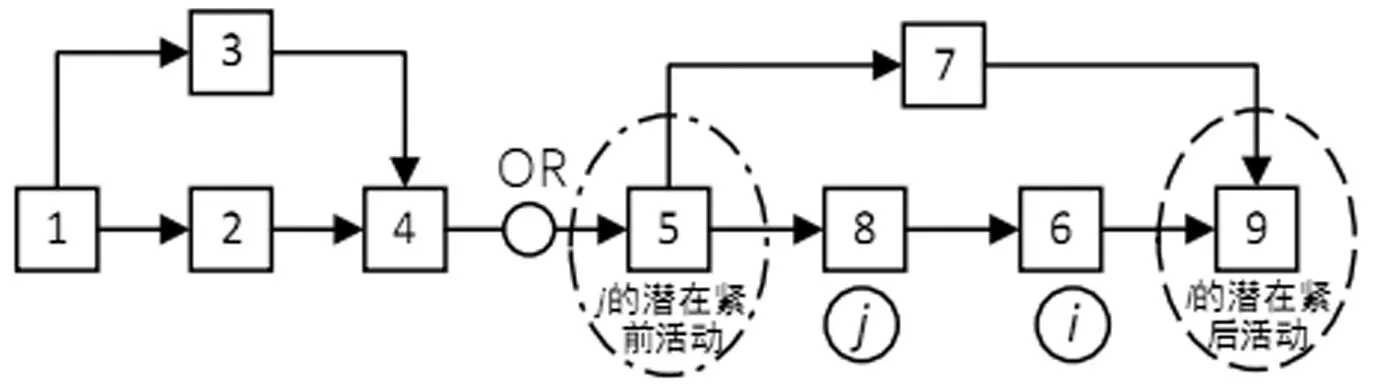
图5 EX-CLUSIVE-OR软逻辑顺序变化后的网络计划图
3)SOFT型软逻辑对紧后活动数量的影响。由于SOFT型软逻辑同时具备OR和EX-CLUSIVE-OR型软逻辑的性质,因此其对紧后活动数量的影响与上述两类软逻辑相同。
1.2 模型构建
采用基于活动的方式,将项目抽象为一个AoN(Activity-on-Node)网络,G=(V,E),其中V为活动集合,V={0,1,…,n,n+1},活动0和活动n+1均为虚活动,分别表示项目的开始与结束。E为有向弧的集合,表示活动间的逻辑关系,其中,E1为固定逻辑关系集合,既包括具有固定逻辑施工顺序的活动间的逻辑关系,也包括软逻辑活动与其他活动的潜在固定逻辑关系,(i,j)∈E1表示活动i结束后活动j才能开始;E2为OR型软逻辑关系集合,(i,j)∈E2表示活动i和j可平行施工,但施工顺序不可互换;E3为EXCLUSIVE-OR型软逻辑关系集合,(i,j)∈E3表示活动i和j的施工顺序可互换,但不可平行施工;E4为SOFT型软逻辑关系集合,(i,j)∈E4表示活动i和j既可改变施工顺序,也可平行施工。活动i(i=0,1,…,n+1)的工期均值为非负整数E(di),实际活动工期受多种不确定性因素的干扰可能在工期均值上下浮动。项目截止日期为δ。需要说明的是,为了充分利用软逻辑,本文暂不考虑资源的约束。
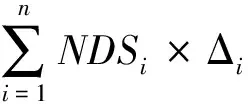
式中,wi表示经过归一化的风险权重,项目管理者根据实际工程经验或者其他判断依据给予活动延误风险权重。
基于上述分析,本文考虑软逻辑的鲁棒调度优化问题可界定为:在活动网络优先关系和项目截止日期约束条件下,确定软逻辑的顺序,并利用时间缓冲添加策略进行主动调度,实现项目工期和鲁棒性的权衡优化。
综上,构建考虑软逻辑的鲁棒项目调度优化模型:
(1)
minT=sn+1
(2)
s.t.si+E(di)+Δi≤sj,(i,j)∈E1
(3)
si+E(di)+Δi≤sj+Mxij,(i,j)∈E2
(4)
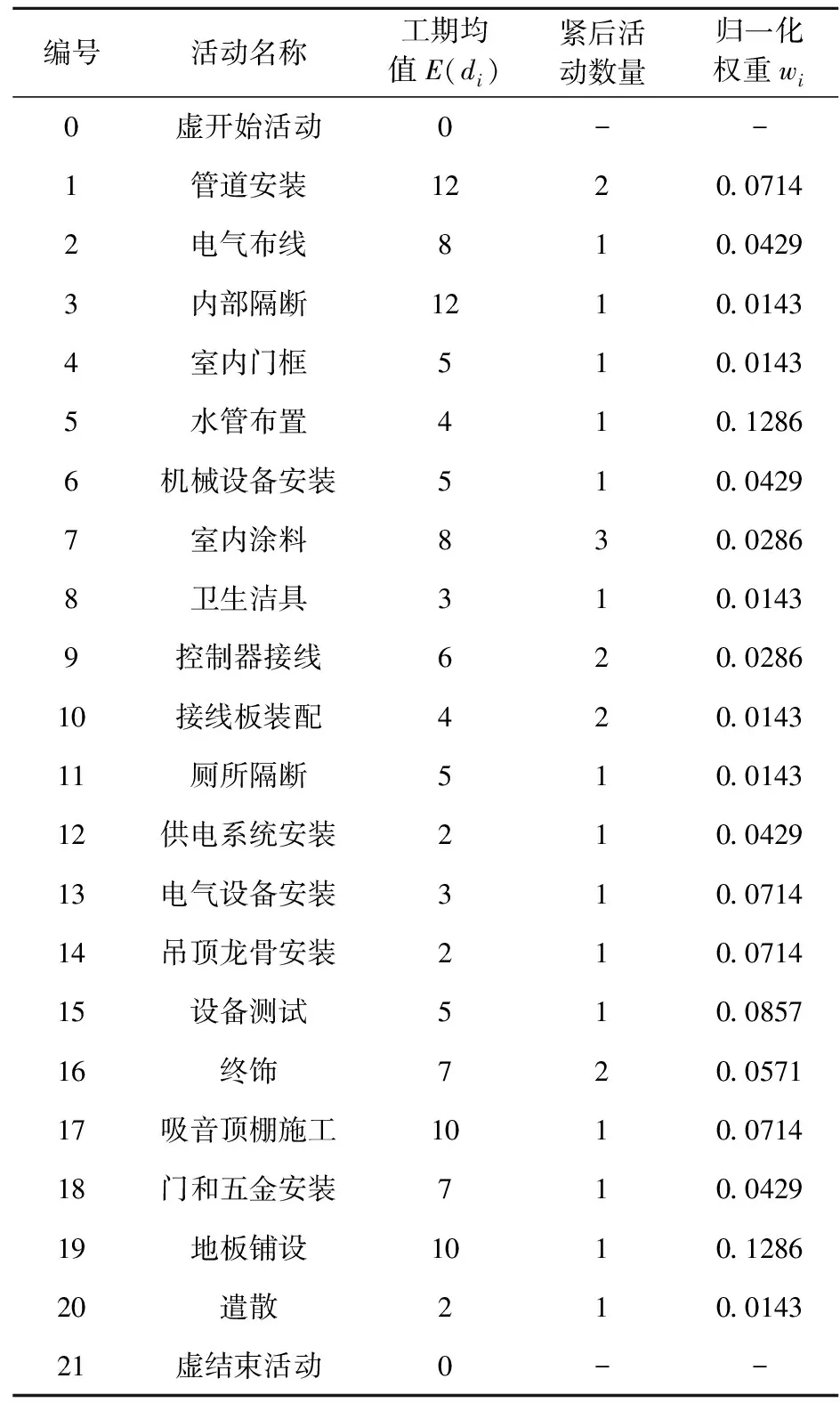
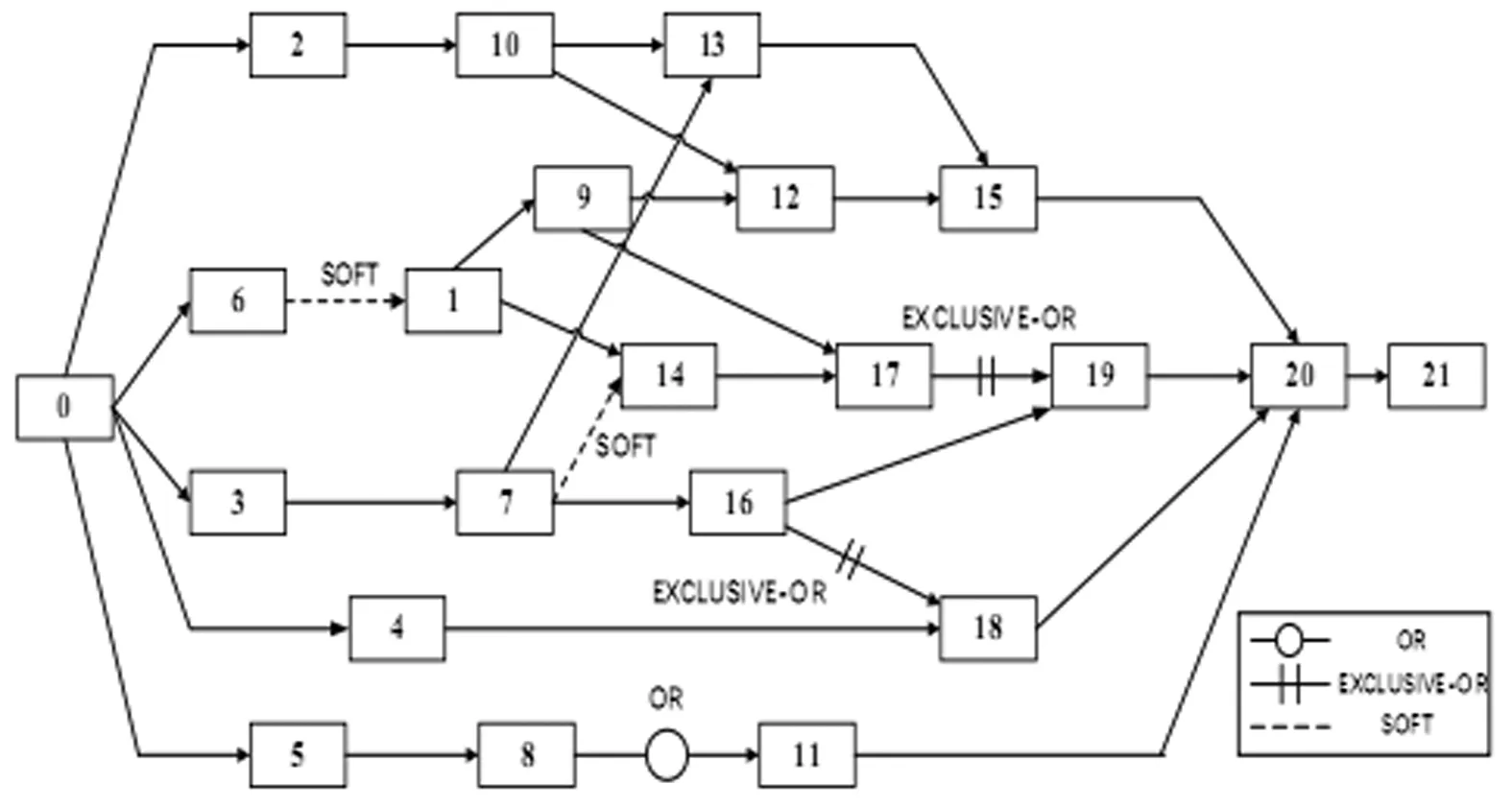
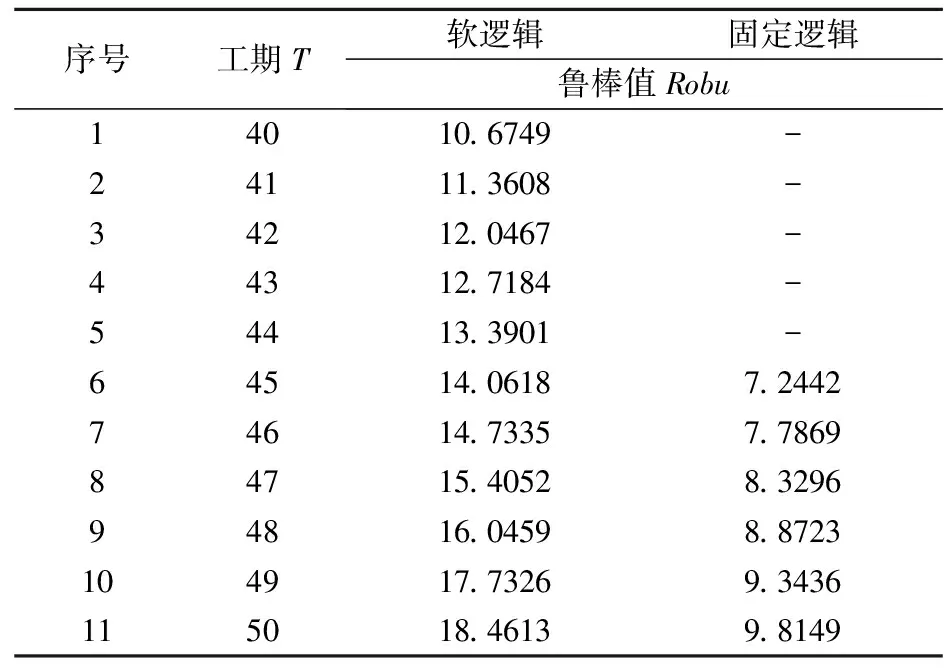
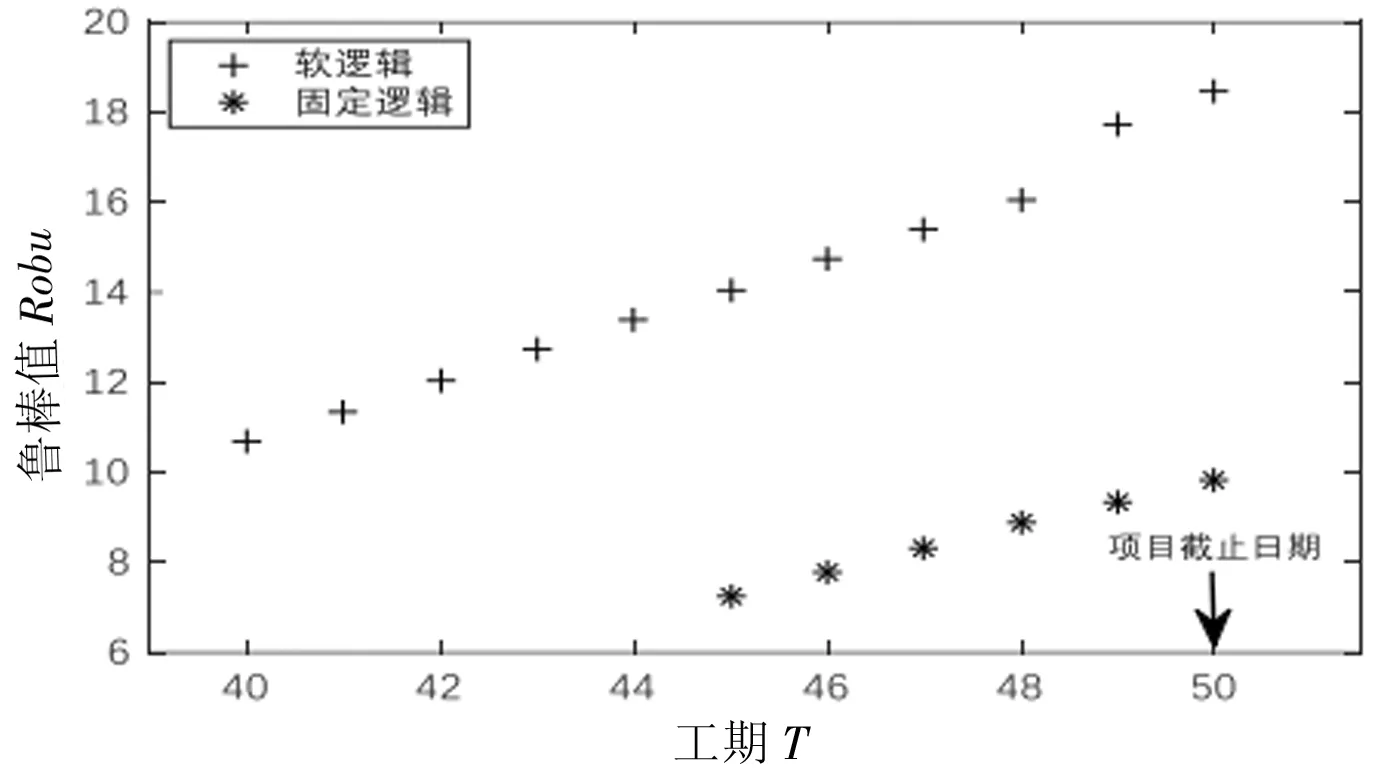
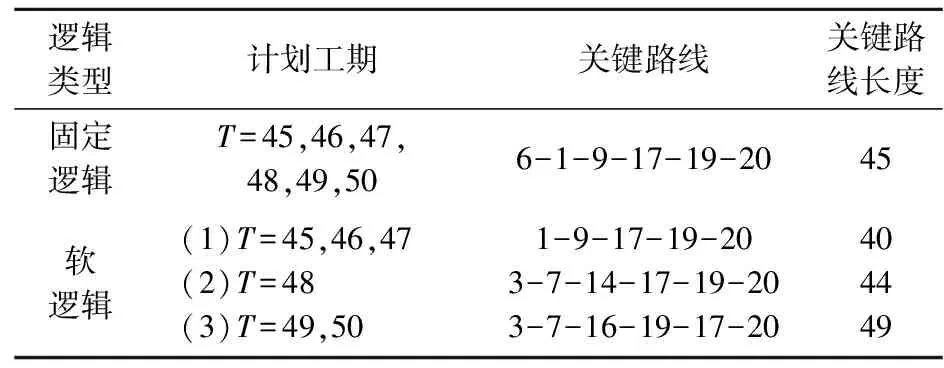
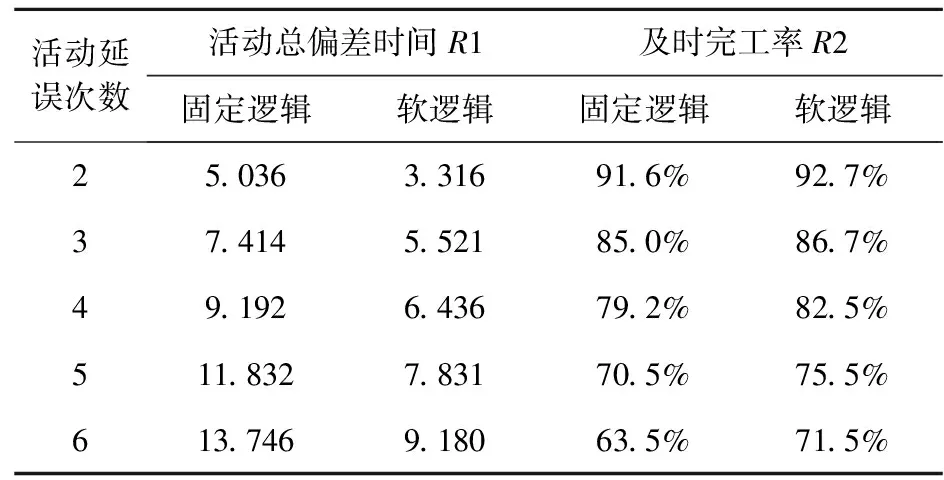
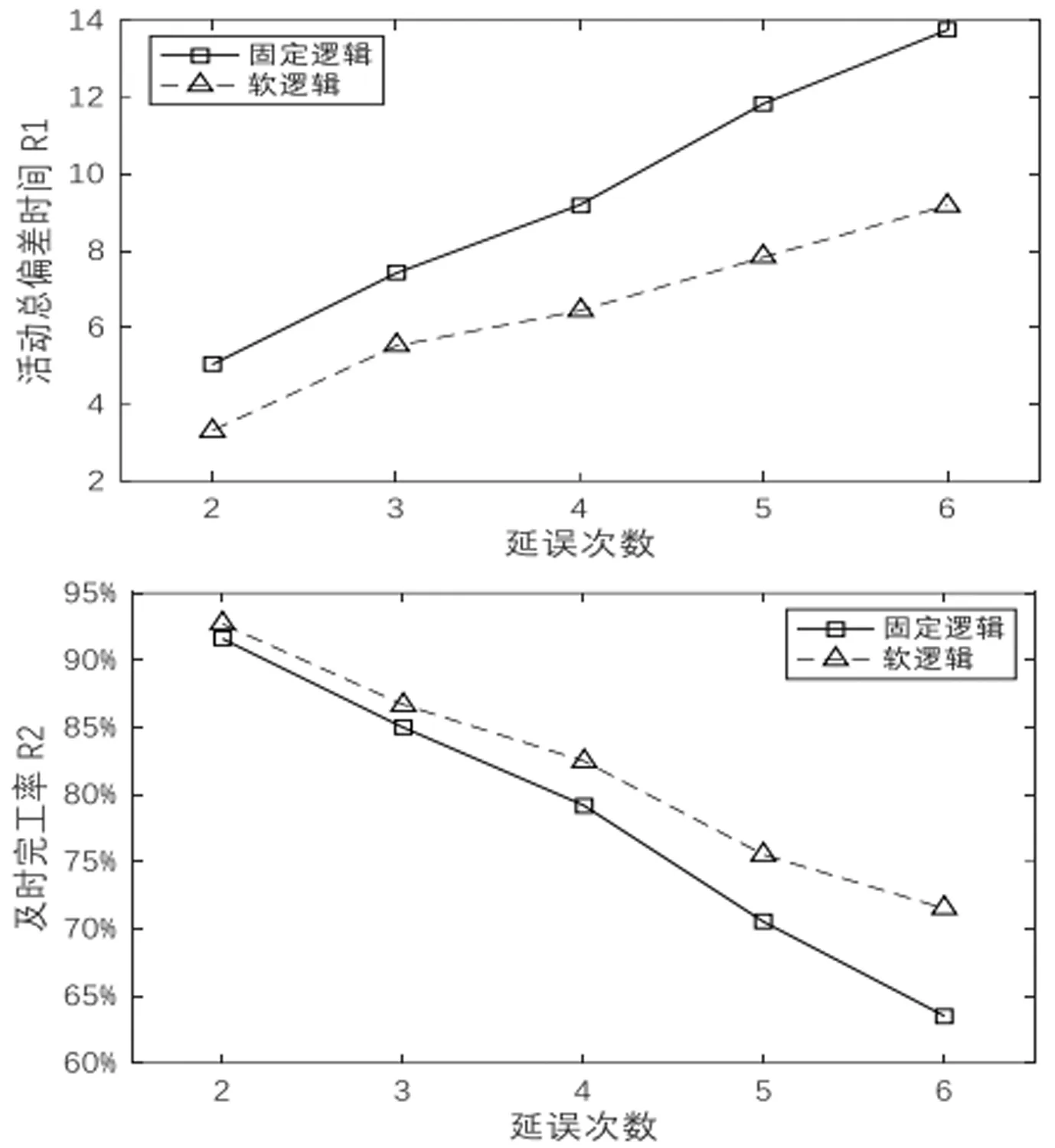
si (5) sj (6) NDSi=NDSi-1+PSi, NDSpprej=NDSpprej+1,(i,j)∈E2,xij=1 (7) si+E(di)+Δi≤sj+Myij,(i,j)∈E3 (8) sj+E(di)+Δj≤si+M(1-yij),(i,j)∈E3 (9) DNSi=NDSi-1+PSi,NDSj=NDSj+1-PSi,(i,j)∈E3,yij=1 (10) (11) (12) (13) (14) (15) (16) NDSi=NDSi-1+PSi,NDSj=NDSj+1-PSi, (17) sn+1≤δ (18) si∈R+,i∈V (19) xij∈{0,1},(i,j)∈E2 (20) yij∈{0,1},(i,j)∈E3 (21) (22) 该模型的目标是同时最小化项目工期和最大化进度计划鲁棒值,故其最优解将会是由多个相互之间无占优关系的单个解组成的Pareto最优解集。e-约束算法具有求解多目标优化问题的能力,可以在有限的步骤中得到所有精确的帕累托解,在文献中得到了广泛的应用,也尤其适合本问题的求解。 e-约束算法的基本理念是:将其中一个目标函数转化为约束,并通过逐步增大e值建立一连串单目标优化问题进行求解。为描述e-约束算法,还需定义以下3类点: 基于本文建立的双目标优化模型中一个目标为最小化,另一个目标为最大化,可以表达e-约束算法如下: 步骤4通过将被支配的点从集合F′中移除,得到Pareto最优前沿F。 本文采用FAN[12]和FAN等[14]共同使用的一个室内建设实际工程案例进行说明,该实际工程案例包括22个活动,图6展示了该项目的计划进度网络,项目合同期限为50天。其中,活动8存在潜在紧后活动20,活动11存在潜在紧前活动5,活动6存在潜在紧后活动9和14,活动17存在潜在紧后活动20。相较于原始案例,本文增加考虑了各活动面临的延误风险大小,并对所有活动的风险权重进行归一化处理。项目相关信息如表1所示。 表1 实际工程案例相关信息 图6 示例工程项目计划进度网络图 为了分析软逻辑对项目工期和鲁棒性的影响,分别求解软逻辑和固定逻辑假设下的双目标鲁棒调度优化问题。在个人电脑(i5-1135G7 CPU,2.4GHz,8G内存)上使用IBM ILOG优化编程语言OPL建模,并用CPLEX V12.8的求解引擎CP Optimizer进行求解。历时约9s,得到该案例的Pareto解集和工期-鲁棒性权衡曲线如表2和图7所示。 表2 双目标优化Pareto解集 图7 最优Pareto前沿曲线对比 从图7中可以明显看出,在工期相同的情况下,软逻辑情形下求得的项目调度方案的鲁棒性都优于固定逻辑情形下得到的方案。以工期为45~50天时的基准调度方案为例,从表2可知,相比固定逻辑,软逻辑情形下的调度方案的解鲁棒值平均增加了87.34%。这是因为软逻辑通过调整活动间的优先关系,使得可添加的缓冲大大增加,从而提高了调度方案的解鲁棒性。 由表2可知,软逻辑情形下得到的调度方案的项目工期最多可以缩短到40天,相比固定逻辑情形下的最短工期45天,项目总工期缩短了12.50%。软逻辑情形下OR型和SOFT型软逻辑顺序都被调整为同时进行,项目网络的关键路线从6→1→9→17→19→20变为1→9→17→19→20。因此,关键路线上的OR型软逻辑可确保项目工期的缩短,这也为时间缓冲的添加腾出更多的空间。 此外,从表2中看出,在项目截止日期50天的约束下,考虑软逻辑得到的可行鲁棒项目调度方案有11个,而不考虑软逻辑得到的可行调度方案只有6个,可行的项目调度方案数量增加了87.8%,因此,考虑软逻辑使项目具有更多可选择的可行调度方案,大大增强了调度的灵活性,这有利于决策者根据项目的实际需求来调整项目的进度计划。 为了探究软逻辑提高鲁棒性的具体途径,在两种逻辑施工顺序假设下得到的鲁棒性最优项目调度中,按照CPM网络计算得到项目的关键路线及其长度,如表3所示。可以看出,固定逻辑条件下,关键路线始终保持不变,而在考虑软逻辑情形下,项目网络的关键路线有所改动,或缩短或延长,但最终都使得调度方案的鲁棒性得以提升。 表3 两种逻辑类型假设下的关键路线 在利用时间缓冲方法得到的鲁棒性最优基准进度计划中,各活动的时间缓冲由两部分组成:网络自发形成的时间缓冲和项目管理者人为添加的时间缓冲。固定逻辑假设下,项目活动优先关系不能改变,因此增加活动的时间缓冲以增强鲁棒性的途径只有一种,即不断地增加人为添加的时间缓冲,与此同时,这会导致工期的不断延长,在项目截止日期的约束下,该途径提升鲁棒性的程度有限。考虑软逻辑情况下,活动优先关系可以改变,除了与固定逻辑一样以延长工期为代价以外,还有以下两种不影响项目工期提高鲁棒性的途径: 1)通过软逻辑减少网络自发形成的时间缓冲,但为人为缓冲的添加留下了空间。如表3中(1)(2)所示,软逻辑通过改变关键路线压缩了项目的工期,工期的缩短一方面会导致项目网络自身形成的时间缓冲减少,另一方面也会带来可插入时间缓冲的增加,当前者对活动自由时差的影响小于后者时,就能提高项目调度的鲁棒性。 2)通过软逻辑增加网络自发形成的时间缓冲。不改变关键路线的情况下,软逻辑可以通过改变非关键路线上的软逻辑顺序,增加非关键活动的时间缓冲,从而提高项目调度的鲁棒性;改变关键路线延长工期的情况下,如表3中(3)所示,工期的延长一方面会导致项目网络自身形成的时间缓冲增加,另一方面也会导致可插入的时间缓冲减少,当前者对活动自由时差的影响大于后者时,也能提高项目调度的鲁棒性。 选取基于软逻辑的最优调度方案以及基于固定逻辑的最优调度方案作为仿真的初始进度计划,计划完工时间都为45天,项目截止日期为50天。假设项目活动延误时间服从自由度为2的卡方分布,由于本算例规模较小,分别将活动工期延误2~6次,并随机生成发生延误的活动编号,利用Matlab 2016a对项目的执行进行模拟,一共模拟1000次,统计结果如表4和图8所示。可以看出,相比固定逻辑,运用本文提出的基于软逻辑的双目标优化模型所求得的基准调度方案,其项目活动执行的稳定性和按时完工的稳定性都更好,抵抗风险的能力也更强,并且随着延误次数的增加,这种差距越来越明显。 表4 蒙特卡洛模拟结果 图8 R1和R2随延误次数变化曲线 上述结果表明,本文提出的基于软逻辑的双目标鲁棒优化模型优化了项目进度计划的解鲁棒性,插入活动的时间缓冲较好地吸收了不确定性因素的干扰,同时也保证了项目在截止日期前完工,使项目调度具有一定的抗风险能力。 本文将软逻辑应用于不确定环境下的项目调度研究,进一步提高调度方案的鲁棒性。论文基于三种类型的软逻辑构建鲁棒性项目调度的双目标优化模型,最小化项目总工期和最大化项目鲁棒值,并运用e-约束算法将双目标模型转换为工期约束下的鲁棒值最大化子模型进行求解。通过一个实际案例对研究问题进行说明,得到了软逻辑能同时优化项目工期和解鲁棒性的结论,并揭示了软逻辑提高鲁棒性的具体途径。最后,通过蒙特卡洛模拟进一步验证模型的有效性。本文研究可以为存在软逻辑的项目的鲁棒进度计划制定提供定量化的决策支持。但是,在工程实际执行过程中,资源的可用量往往是有限的,软逻辑的改变也会导致资源需求量的变化,因此后续将进行考虑软逻辑的资源约束型鲁棒项目调度问题研究。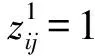
2 算法设计
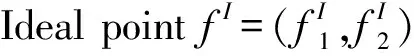
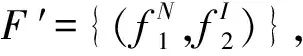
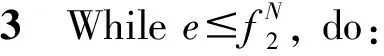
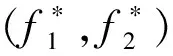
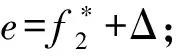
3 算例分析
3.1 项目背景
3.2 结果分析
3.3 软逻辑提高项目鲁棒性的途径
3.4 蒙特卡洛模拟分析
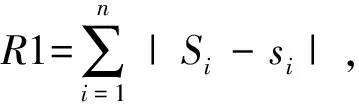
4 结束语

