预热温度对机匣等离子喷涂铝硅可磨耗封严涂层应力场影响的数值模拟

苏宇航，温祯洪，罗军明，崔世宇

预热温度对机匣等离子喷涂铝硅可磨耗封严涂层应力场影响的数值模拟

苏宇航，温祯洪*，罗军明，崔世宇

（南昌航空大学 材料科学与工程学院，南昌 330063）

为确定机匣等离子喷涂铝硅涂层最佳预热温度，揭示不同预热温度对涂层残余应力的影响，优化基体预热温度，降低由于过大的残余应力导致涂层剥落和失效的可能性，为实际生产提供指导。基于热弹塑性有限元理论，使用ANSYSWORKBENCH中稳态热和结构应力模块，建立双层等离子喷涂有限元模型。采用间接热力耦合方法对不同预热温度下的机匣等离子喷涂温度场和应力场进行模拟，分析不同预热温度对面层/黏结层/基体系统温度和应力分布的影响，重点研究了预热温度为30、50、80、120、150、180、200 ℃时涂层的温度场和应力场分布。随着基体预热温度的升高，基体和涂层的温度梯度逐渐减小，面层等效应力逐渐减小，最大等效应力先减小后增大；轴环向应力和轴轴向应力分布及变化趋势基本相同；与轴环向应力和轴轴向应力相比，基体预热温度的变化对轴径向拉应力、径向压应力的影响更大。根据涂层的残余应力的分布和变化规律，等离子喷涂铝硅可磨耗封严涂层时，基体预热温度应控制在150 ℃。

铝硅封严涂层；预热温度；应力场；数值模拟

作为航空发动机制造的重要技术之一，采用等离子喷涂技术在压气机的机匣上制备封严涂层，改善机匣与叶片之间的密封性，减小间隙，提高热效率，显著提高发动机性能[1]。在材料和装备领域，残余应力是各种加工使用过程中伴随力或温度或比容积等力学物理性能差异三大因素之一，或多个因素耦合而引起的弹/塑性变形不均匀性而产生的力学欠缺或缺陷，在物体内部自相平衡的应力状态。哪里有弹/塑性变形不均匀性或不匹配，哪里就有残余应力存 在[2]。由于采用等离子喷涂作为机匣涂层喷涂技术，在喷涂过程中会出现急热、骤冷现象，基体、黏结层和面层材料的热物理性能之间通常存在差异，因此喷涂期间易对加工工件及涂层产生残余应力，而涂层残余应力是导致涂层开裂和剥落的主要原因之一，所以降低涂层残余应力是十分重要的。等离子喷涂前需要对基体进行预热处理，优化基体的预热温度，能够降低熔滴的冷却速度，提高涂层整体温度分布的均匀性，降低涂层的热应力，从而降低涂层残余应力[3]。因此，研究基体预热温度对涂层残余应力的影响具有重要意义。

由于热喷涂过程中熔滴撞击速度快、温度高、凝固时间短，通过实验手段很难获得喷涂过程中温度场及应力场数据，且实验受环境因素影响，偶然因素多，难以得到准确的结果，所以为了准确分析不同参数的影响同时避免实际中大量的实验工作，本研究采用数值模拟方法，模拟不同预热温度对涂层残余应力的影响，得出的结果对涂层制备具有指导意义。

近年来，关于涂层应力场数值模拟的研究已有阶段性进展。Pang等[4]使用ANSYS研究了等离子喷涂Mo/8YSZ梯度功能热障涂层在不同预热温度下涂层残余应力的影响，研究表明随着基体预热温度的提高，涂层轴向残余拉应力分布范围增大，轴向残余压应力分布范围逐渐减小，基体的径向残余拉应力最大值、径向残余压应力最大值和轴向残余压应力最大值增大，但基体的轴向残余拉应力最大值呈现先减小后增大的趋势。Liu等[5]提出了一种动态预热方法，即在移动熔池前增加一个热源来局部加热，建立三维有限元模型，研究了动态预热对多轨迹多层激光熔覆的影响，结果表明，动态预热可以使各层温度梯度显著减小，冷却速率显著降低。Deng等[6]用等离子喷涂设备，在不同温度下在铬镍铁合金表面制备了钇稳定氧化锆涂层，研究了基体预热温度对涂层显微组织和力学性能的影响，研究发现，当基体预热温度为800 ℃时，涂层的硬度、韧性、界面结合强度和抗气蚀性最佳。Sadhu等[7]研究了基体预热温度对铬镍铁合金718直接激光沉积NiCrSiBC-60%WC陶瓷涂层裂纹缓解的影响，研究表明通过改变扫描速度来改变冷却速度并不能缓解裂纹，为了降低冷却速度和温度梯度只能采用不同的基体预热温度。Xie等[8]、Yu等[9]讨论了预热温度对喷涂颗粒黏附强度和变形行为的影响，结果表明，使用预热颗粒可以获得较强的黏附强度。但当颗粒预热温度过高时，颗粒的黏附强度降低。Rezvani等[10]、侯平均等[11]建立了具有真实粗糙度和真实孔隙率的有限元模型，考虑了黏结层和面层的沉积过程，更贴合实际地研究了预热温度对残余应力的影响。

有限元模拟作为一种有效的科学研究方法，可以高效、准确地获得计算对象的应力分布，近年来被热喷涂领域的研究学者广泛应用，然而目前针对等离子喷涂铝硅可磨耗封严涂层的预热处理对涂层残余应力影响的数值模拟未见报道。为了揭示不同预热温度对涂层残余应力的影响，确定等离子喷涂铝硅涂层的最佳预热温度，本研究基于ANSYSWORKBENCH[12]有限元分析，以航空发动机机匣涂层为研究对象，建立涂层增层力学模型，对不同预热温度下等离子喷涂铝硅涂层进行热力耦合模拟[13-14]，计算涂层温度场、应力场的变化情况。采用数值模拟研究预热温度对基体和涂层温度场与应力场的影响，为实际涂层制备工艺优化提供参考数据。

1 研究方法

1.1 数学模型建立

因基体温度不同时，面层/黏结层/基体系统的应力状态不同，总有一个最佳基体温度使面层/黏结层/基体系统的总残余应力最小。系统的总残余应力由淬火应力、温升残余应力和喷射冲击残余应力构成。等离子喷涂过程中，喷涂颗粒被高温等离子射流加热至熔融或半熔融状态，并以高速撞击基体或沉积在涂层的上表面，与基体或沉积的层状结构相比，熔滴的温度更高，在温差的作用下，熔滴会凝结收缩，但由于基体或层状结构的约束，熔滴的收缩不能自由发生，这种由于淬火效应而产生的残余应力称为“淬火应力”。当基体温度改变时，淬火应力和温升残余应力受影响最大，由表达式（1）中可以看出：

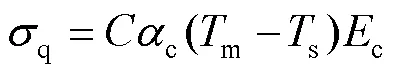
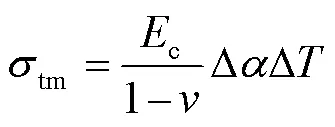
因此，系统的总残余应力为：

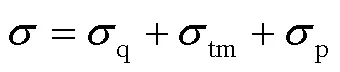
1.2 热弹塑性有限元理论

在等离子喷涂过程中，基体与高温等离子射流相互作用时，粉末颗粒与基体的撞击会产生弹性变形和塑性变形。材料的热弹塑性增量本构方程为：

1.3 有限元模型建立及边界条件确定

1.3.1 模型建立及网格划分

本文模拟在材料为0Cr16Ni4Cu3Nb的机匣基体上喷涂制备铝硅涂层。建立的模型以飞机发动机机匣[19]为原型并加以简化如图1所示，基体是高度为100 mm、外径为227 mm、厚度为3.5 mm的空心圆柱体。涂层位于圆柱形基体的中间内壁，黏结层和面层宽度均为20 mm，厚度分别为0.15 mm和1.2 mm。

网格划分的目的在于将求解区域分解成合适数量的离散单元以便得到较为精确的结果。因为等离子喷涂过程是一个急热骤冷的过程，其喷涂区域温度梯度变化很大，所以在中间内壁处网格划分一般选用密集网格，而远离喷涂处的区域采用相对稀疏的网格，可以精确喷涂区域的计算和减少计算时间[20]。为了避免盲目性，对涂层部分的网格参数设置了5组比较试验，以比较单元数、操作时间和计算结果，如表1所示。通过比较，可以得出结论：1）随着单元数的增加，得到的应力值趋于稳定，但网格越细，可能不会更准确；2）随着单元数的增加，计算机CPU的计算时间也会增加；3）通过比较5组参数的计算结果，最优网格参数为1.25 mm，模型计算时间更短，网格数计算结果更准确。最终网格划分结果如图1所示，共有124 558个节点和27 805个单元。图1c为网格质量衡量指标，可以看出对涂层部分的网格加密后，平均质量为0.827，网格质量在0.9～0.99范围内的单元数量占65%。

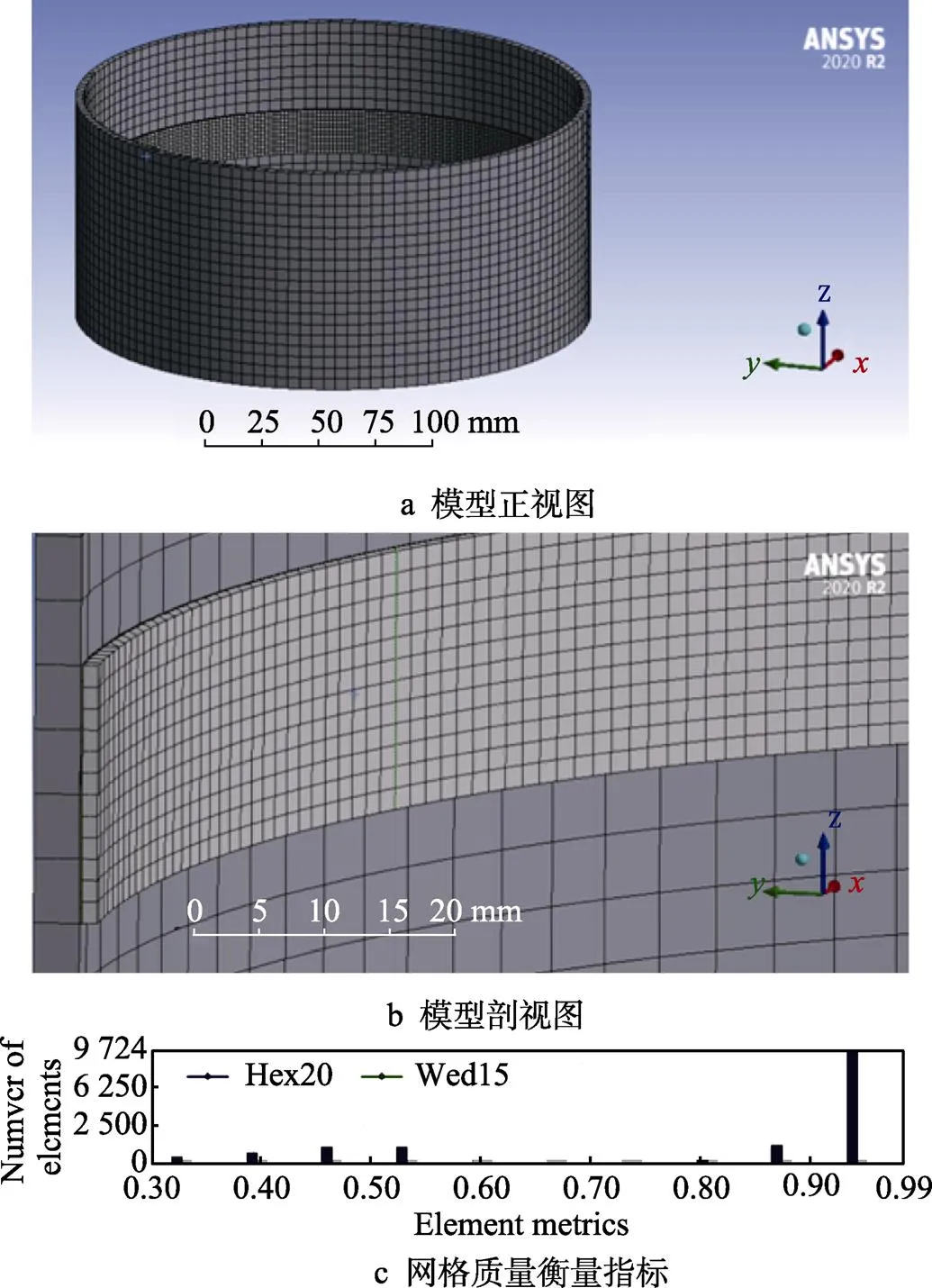
图1 网格划分示意图

Fig.1 Schematic diagram of grid division: a) front view of the model; b) sectional view of the model; c) element metrics

表1 5组网格参数及对比结果

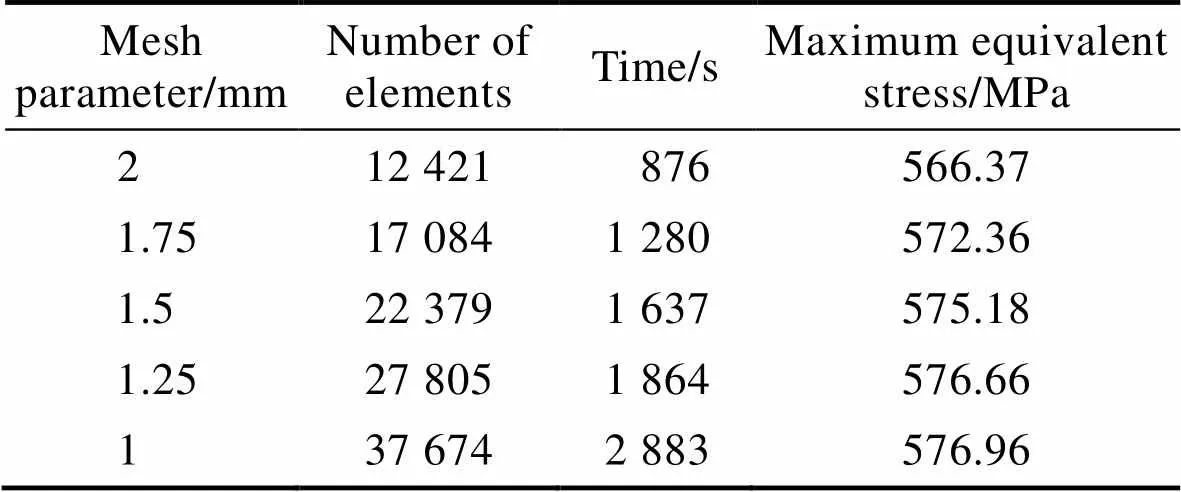
Tab.1 Comparison results of five groups of grid parameters

1.3.2 材料参数的设定

模拟喷涂的温度场和应力场必须确定材料的密度、杨氏模量、泊松比、比热容、热膨胀系数和导热率，考虑了材料的热物理性能参数随温度的变化，见表2～4。

1.3.3 物理模型和边界条件

由于机匣等离子喷涂过程涉及多种瞬态效应，与诸多因素密切相关，例如熔滴沉积[24]、随温度变化的热物性参数[25]和涂层系统的缺陷[26]等。为简化研究不同预热温度对喷涂过程的影响，对该等离子喷涂模型作如下假设：1）预热温度和涂层温度状态都是稳态[27]，模拟喷涂结束后基体/涂层系统的应力状态；2）层与层间的界面处结合光滑且牢固；3）忽略涂层内部孔隙；4）不考虑热流密度、扫描速度等喷涂工艺参数[28]对涂层温度的影响。

基体的初始预热温度分别设为30、50、80、120、150、180、200 ℃，涂层温度设为350 ℃，周围环境温度为22 ℃，不考虑辐射和对流的影响。喷涂开始前，工件垂直放置在工作平台上，因此工件模型的底面是固定的，整个组件处于无应力初始状态。

表2 基体0Cr16Ni4Cu3Nb热物理性能参数[21]

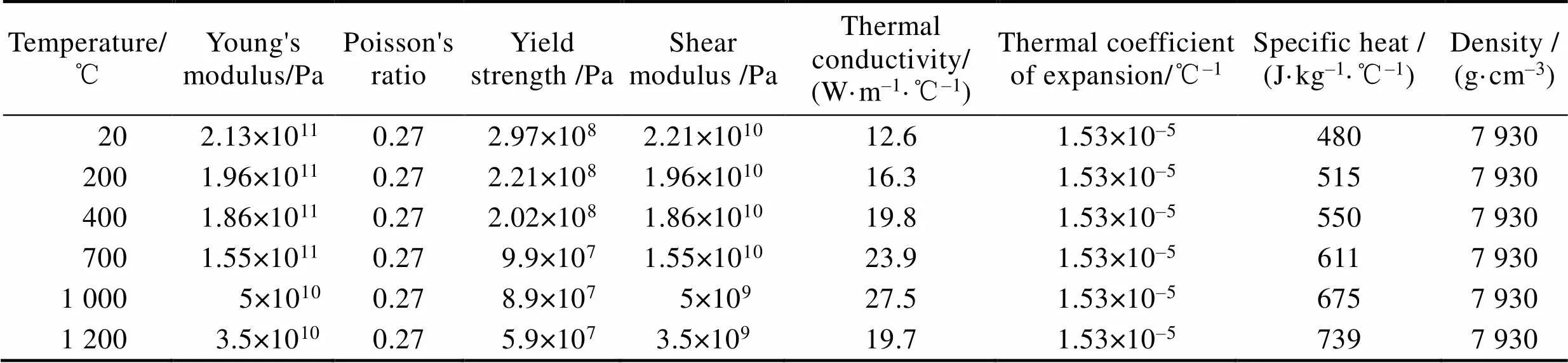
Tab.2 Performance parameters of substrate[21]

表3 黏结层Ni-Al5%热物理性能参数[22]

Tab.3 Performance parameters of bond layer[22]

续表3

表4 面层Al-Si12%热物理性能参数[23]

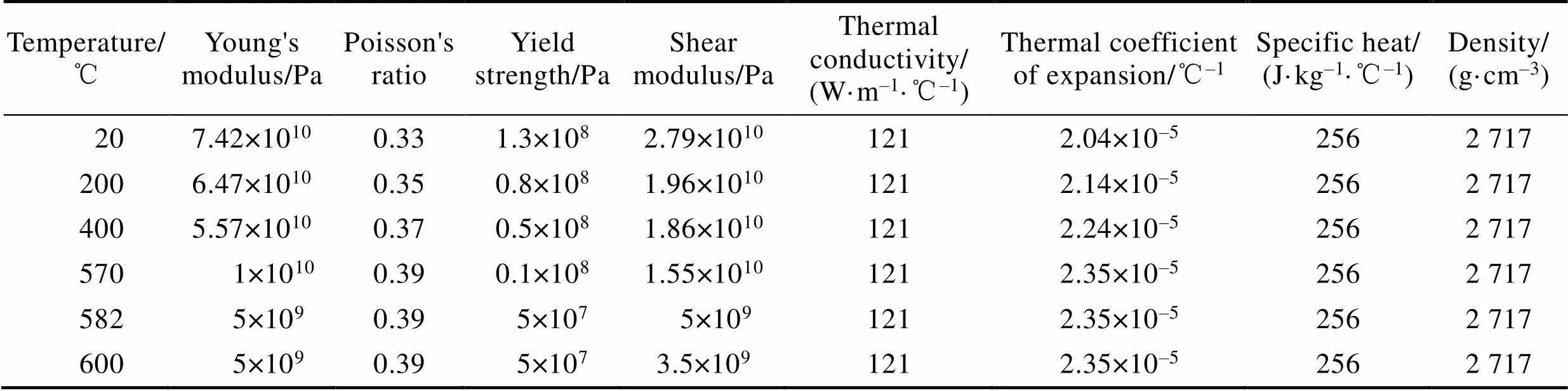
Tab.4 Performance parameters of top layer[23]

2 数值模拟结果及分析

2.1 不同预热温度下涂层温度场模拟结果及分析

利用Temperature命令[29]施加温度载荷，求解出温度场如图2～8所示（图中温度单位为℃）。当预热温度从30 ℃提高到200 ℃时，基体与涂层界面的平均温度从47.78 ℃上升到208.33 ℃，通过对7组不同预热温度下得到的温度场云图进行观察比较，可以发现基体与面层间存在热传导，在基体预热温度逐渐提高、涂层温度不变的情况下，基体和涂层间的温度梯度逐渐减小，基体与涂层结合界面处的温度逐渐提高，且基体与涂层间的温度分布规律大致相同，即离涂层表面越远，温度越低。

图2 预热温度为30 ℃下的温度场

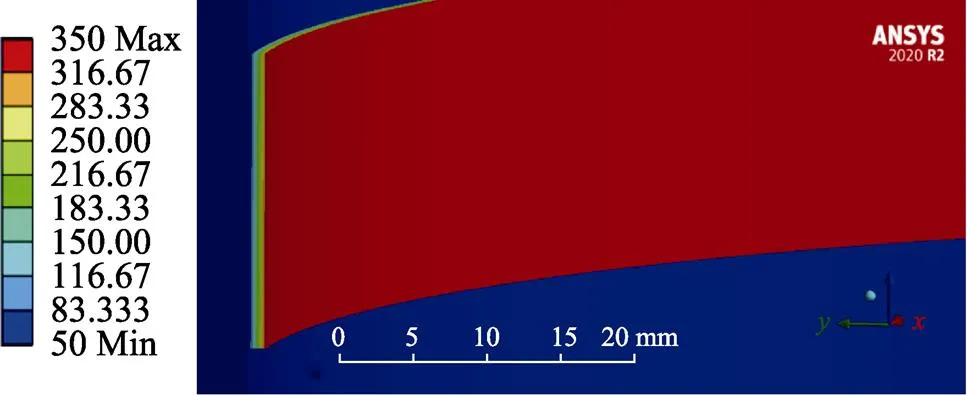
图3 预热温度为50 ℃下的温度场

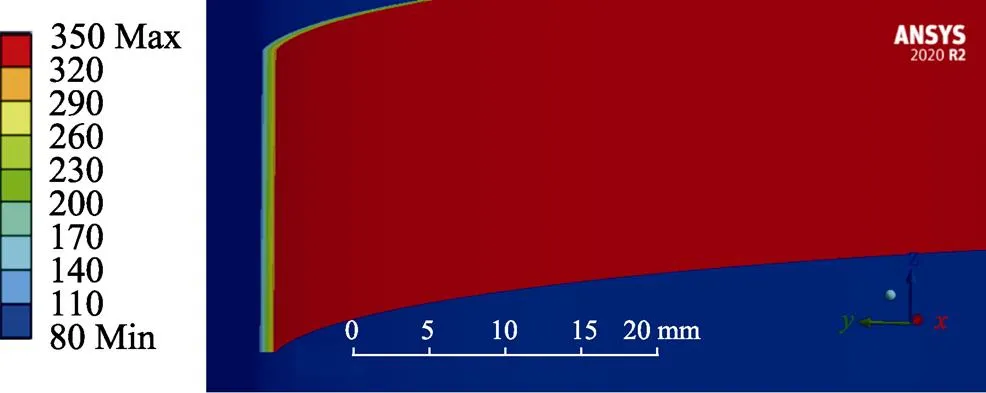
图4 预热温度为80 ℃下的温度场

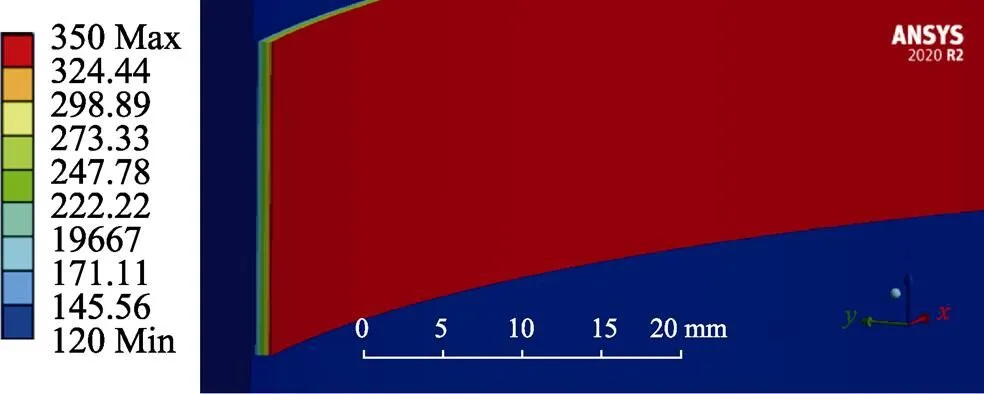
图5 预热温度为120℃下的温度场

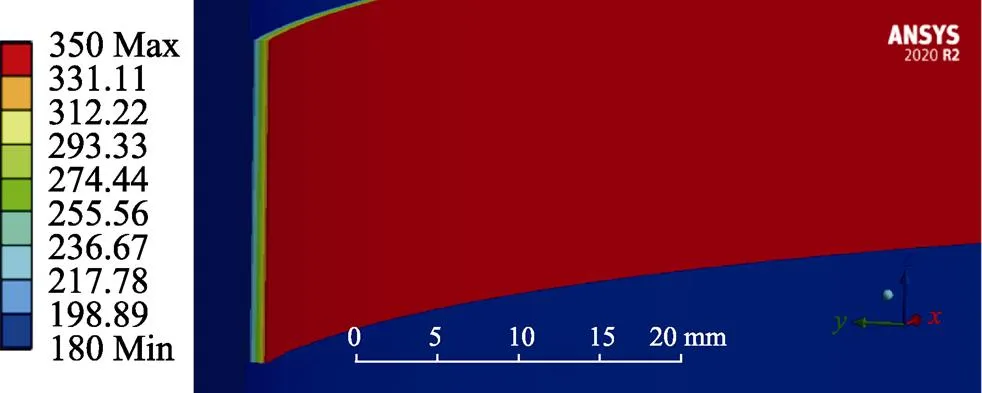
图7 预热温度为180 ℃下的温度场

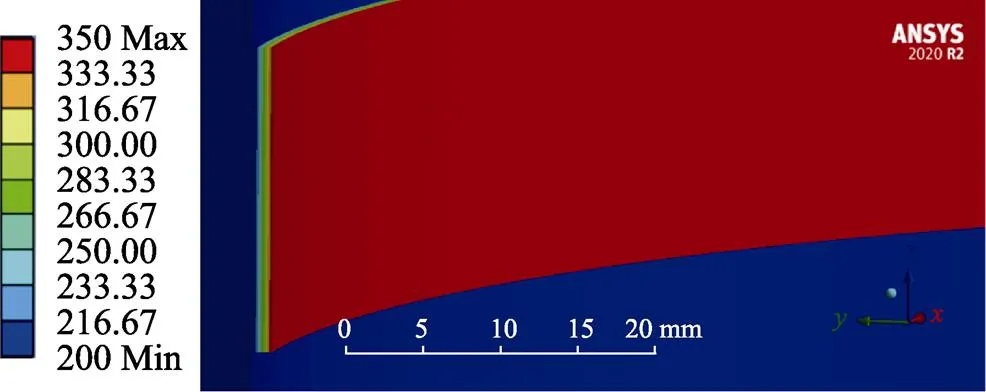
图8 预热温度为200 ℃下的温度场

2.2 不同预热温度下涂层应力场模拟结果及分析

采用间接耦合法，将所求得的所有节点温度作为载荷施加到结构应力分析中[30]，在理论上假定基体/涂层应力场服从冯·米塞斯（Von-Mises）屈服准则[31]，求出等效应力场（Equivalent Stress），依据如图9所示的柱坐标系，插入正应力（Normal Stress）[32]命令，得到沿轴径向应力、轴环向应力、轴轴向应力云图（图中应力单位为MPa，正值为拉应力，负值为压应力）。

图10为预热温度为30 ℃下的应力场云图。从图10a中可以看出预热温度为30 ℃时，最大等效应力位于面层表面，达到576.66 MPa，应力值由面层表面向基体方向递减，基体和黏结层内等效应力值处于较低水平；从图10b中可以看出沿轴径向方向，基体处于拉应力状态，黏结层和面层呈现为涂层中间为拉应力状态，涂层两侧边缘部分为压应力状态，且最大压应力位于黏结层与面层结合边缘处达到328.55 MPa；从图10c中可以看出，沿轴环向方向，最大拉应力位于基体处达到65.212 MPa，黏结层中间部分处于拉应力状态，黏结层边缘部分处于压应力状态，面层部分处于压应力状态且最大压应力位于面层表面达到608.2 MPa，压应力呈现由面层中间向边缘两侧递减的规律，距离面层越远，压应力越小的规律；从图10d中可以看出，沿轴轴向方向，拉应力集中在基体和黏结层结合界面处达到229.53 MPa，且应力以此界面为界限分别向基体和面层方向递减，到达基体表面时应力状态转变为压应力状态，到达面层表面时达到最大压应力为540.92 MPa。

图9 几何模型的柱坐标系

图11为预热温度为50 ℃下的应力场云图。从图11a中可以看出，预热温度为50 ℃时，最大等效应力位于面层表面，达到555.74 MPa；从图11b中可以看出，沿轴径向方向，基体处于拉应力状态，最大拉应力集中在黏结层和面层结合界面处达到146.11 MPa，最大压应力集中在黏结层和面层结合边缘处达到317.15 MPa；从图11c中可以看出，沿轴环向方向，最大拉应力位于基体处达到66.093 MPa，涂层部分处于压应力状态且最大压应力位于面层表面达到586.94 MPa，与预热温度为30 ℃时不同的是此时黏结层也为压应力状态；从图11d中可以看出，沿轴轴向方向，最大拉应力集中在基体和黏结层结合界面处达到230 MPa，且应力以此界面为界限分别向基体和面层方向递减，到达基体表面时应力状态转变为压应力状态，到达面层表面时达到最大压应力为519.73 MPa。

图12为预热温度为80 ℃下的应力场云图。从图12a中可以看出，在预热温度为80 ℃时，最大等效应力位于面层表面，达到524.62 MPa；从图12b中可以看出，沿轴径向方向，基体和部分涂层部位处于压应力状态且应力分布均匀，最大拉应力位于黏结层和面层结合界面处达到140.53 MPa，最大压应力位于黏结层和面层结合边缘处达到339.15 MPa；从图12c中可以看出，沿轴环向方向，最大拉应力位于基体处达到67.416 MPa，涂层部分处于压应力状态且最大压应力位于面层表面达到555.35 MPa；从图12d中可以看出，沿轴轴向方向，最大拉应力集中在基体和黏结层结合界面处达到230.7 MPa，且应力以此界面为界限分别向基体和面层方向递减，到达基体表面时应力状态转变为压应力状态，到达面层表面时达到最大压应力为487.93 MPa。

图10 预热温度为30 ℃下的应力场云图

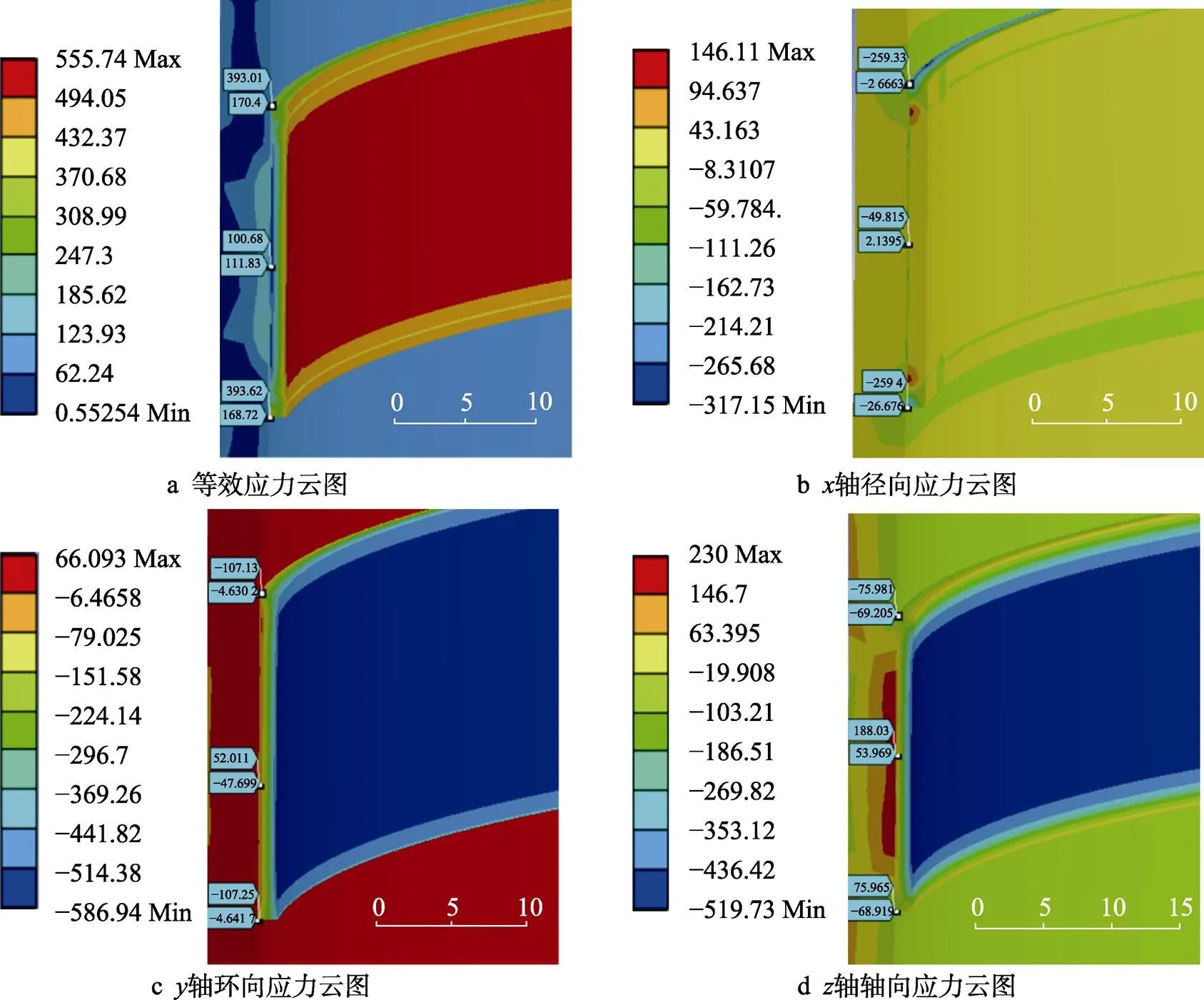
图11 预热温度为50 ℃下的应力场云图

图12 预热温度为80 ℃下的应力场云图

图13为预热温度为120 ℃下的应力场云图。从图13a中可以看出，在预热温度为120 ℃时，最大等效应力位于面层表面，达到483.5 MPa；从图13b中可以看出，沿轴径向方向，基体处于低水平拉应力状态，最大拉应力位于黏结层和面层结合界面处达到133.08 MPa，最大压应力集中在黏结层和面层结合边缘处达到485.58 MPa；从图13c中可以看出，沿轴环向方向，最大拉应力集中在基体内部达到69.179 MPa，基体部分表面呈现压应力状态，涂层部分处于压应力状态且最大压应力位于面层表面达到515.08 MPa；从图13d中可以看出，沿轴轴向方向，最大拉应力集中在基体和黏结层结合界面处达到232.16 MPa，应力以此界面为界限分别向基体和面层方向递减，到达基体表面时应力状态转变为压应力状态，到达面层表面时达到最大压应力为445.54 MPa。

图14为预热温度为150 ℃下的应力场云图。从图14a中可以看出，在预热温度为150 ℃时，最大等效应力依旧集中在面层表面达到453.09 MPa；从图14b中可以看出，沿轴径向方向，基体和部分面层部位处于拉应力状态且应力分布均匀，最大拉应力位于黏结层和面层结合界面处达到127.5 MPa，最大压应力集中在黏结层和面层结合边缘处达到598.53 MPa；从图14c中可以看出，沿轴环向方向，最大拉应力集中在基体内部达到70.502 MPa，基体部分表面呈现压应力状态，涂层部分处于压应力状态且最大压应力位于面层表面达到484.88 MPa；从图14d中可以看出，沿轴轴向方向，最大拉应力集中在基体和黏结层结合界面处达到233.69 MPa，应力以此界面为界限分别向基体和面层方向递减，到达基体表面时应力状态转变为压应力状态，到达面层表面时达到最大压应力为413.92 MPa。

图15为预热温度为180 ℃下的应力场云图。从图15a中可以看出，在预热温度为180 ℃时，最大等效应力分布相较于之前有了显著变化，位于黏结层和面层结合边缘处，达到479.76 MPa，面层表面应力约为411.28 MPa；从图15b中可以看出，沿轴径向方向，基体和部分涂层部位处于拉应力状态且应力分布均匀，最大拉应力位于黏结层和面层结合界面处达到121.91 MPa，最大压应力集中在黏结层和面层结合边缘处达到711.47 MPa；从图15c中可以看出，沿轴环向方向，涂层部分处于压应力状态且最大压应力位于面层表面达到481.85 MPa，最大拉应力集中在基体内部达到71.824 MPa，基体部分表面呈现压应力状态；从图15d中可以看出，沿轴轴向方向，最大拉应力集中在基体和黏结层结合界面处达到235.32 MPa，应力以此界面为界限分别向基体和面层方向递减，到达基体表面时应力状态转变为压应力状态，到达黏结层和面层结合边缘处时达到最大压应力为475.84 MPa，面层表面应力值约为396.82 MPa。

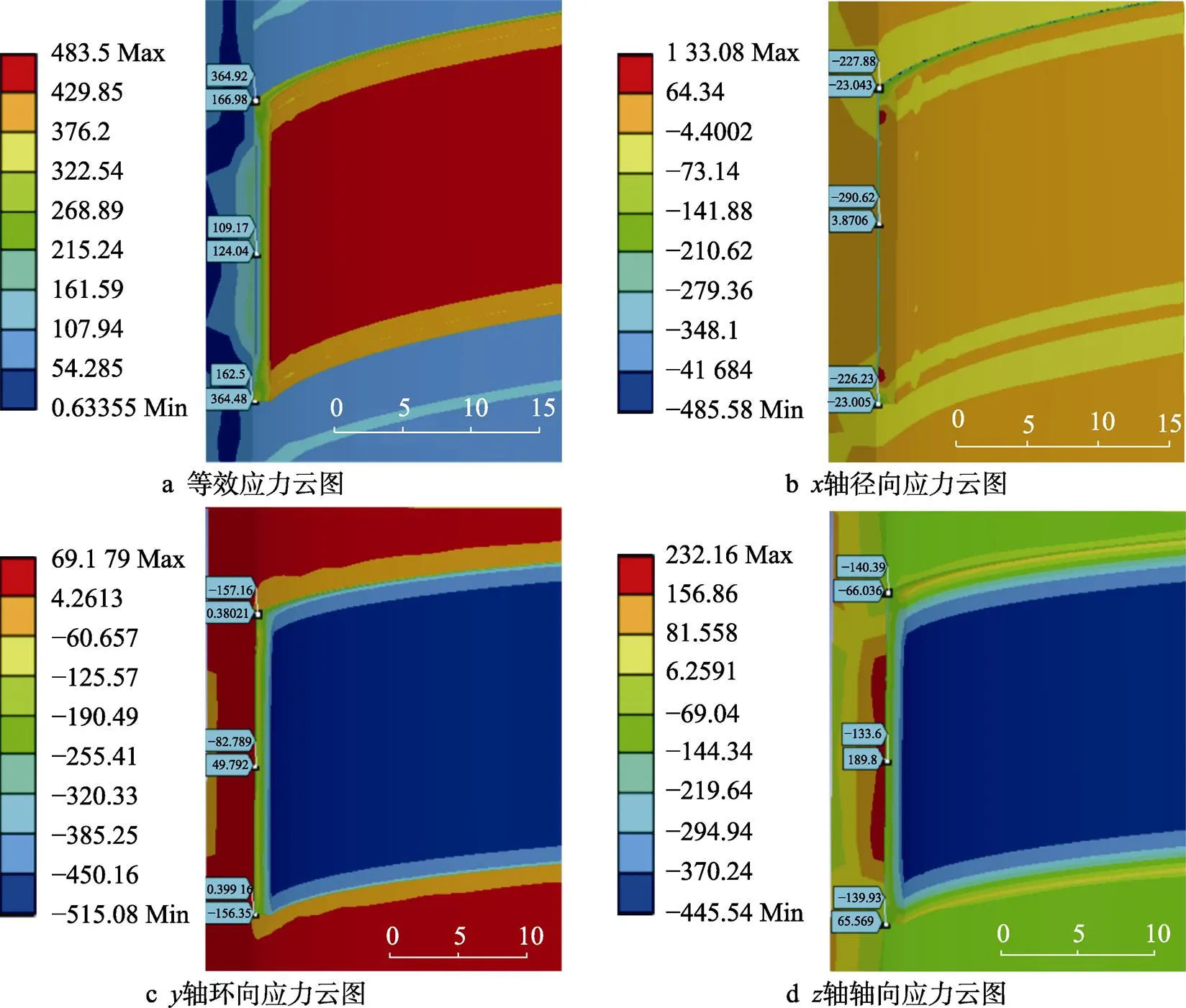
图13 预热温度为120 ℃下的应力场云图

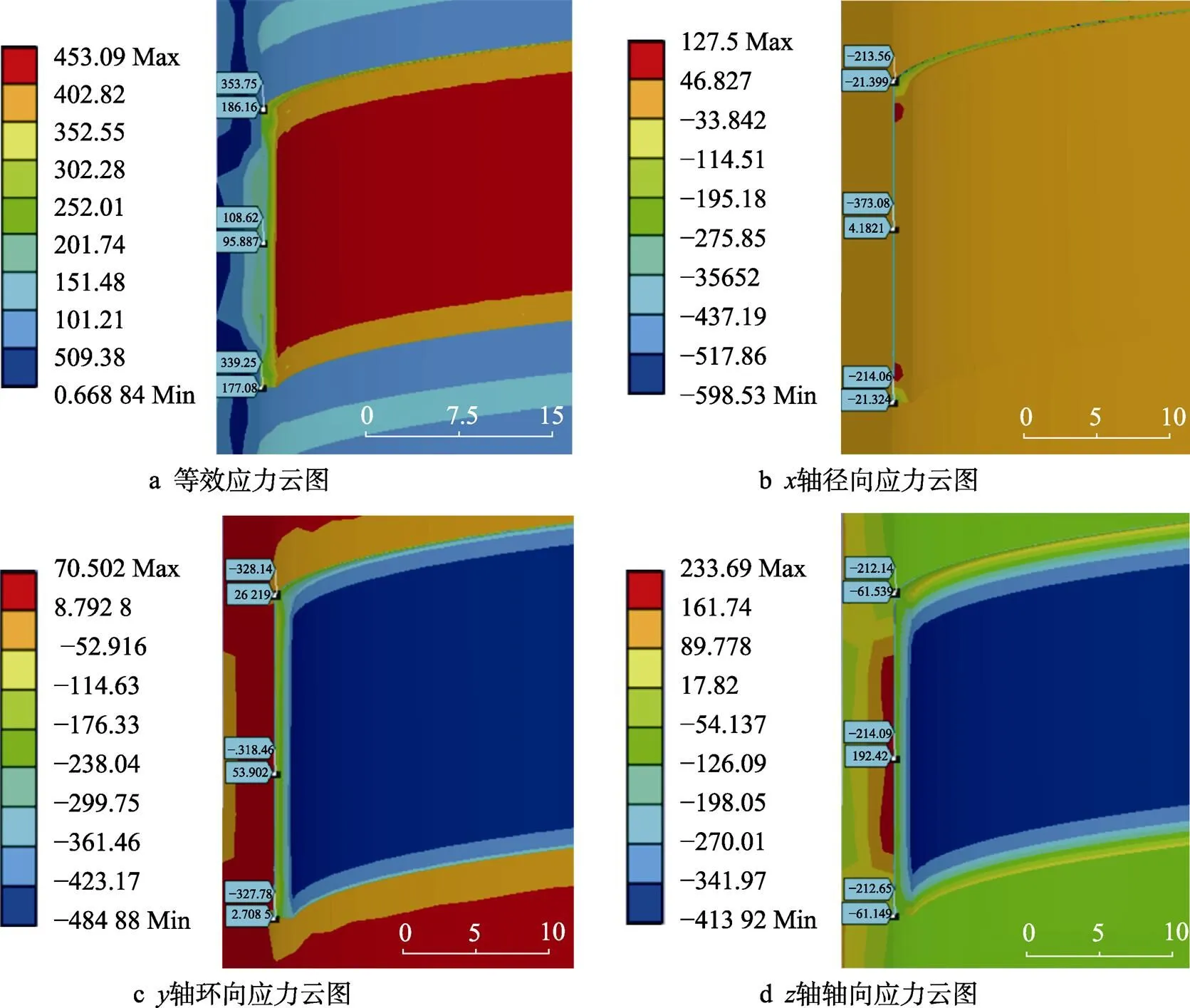
图14 预热温度为150 ℃下的应力场云图

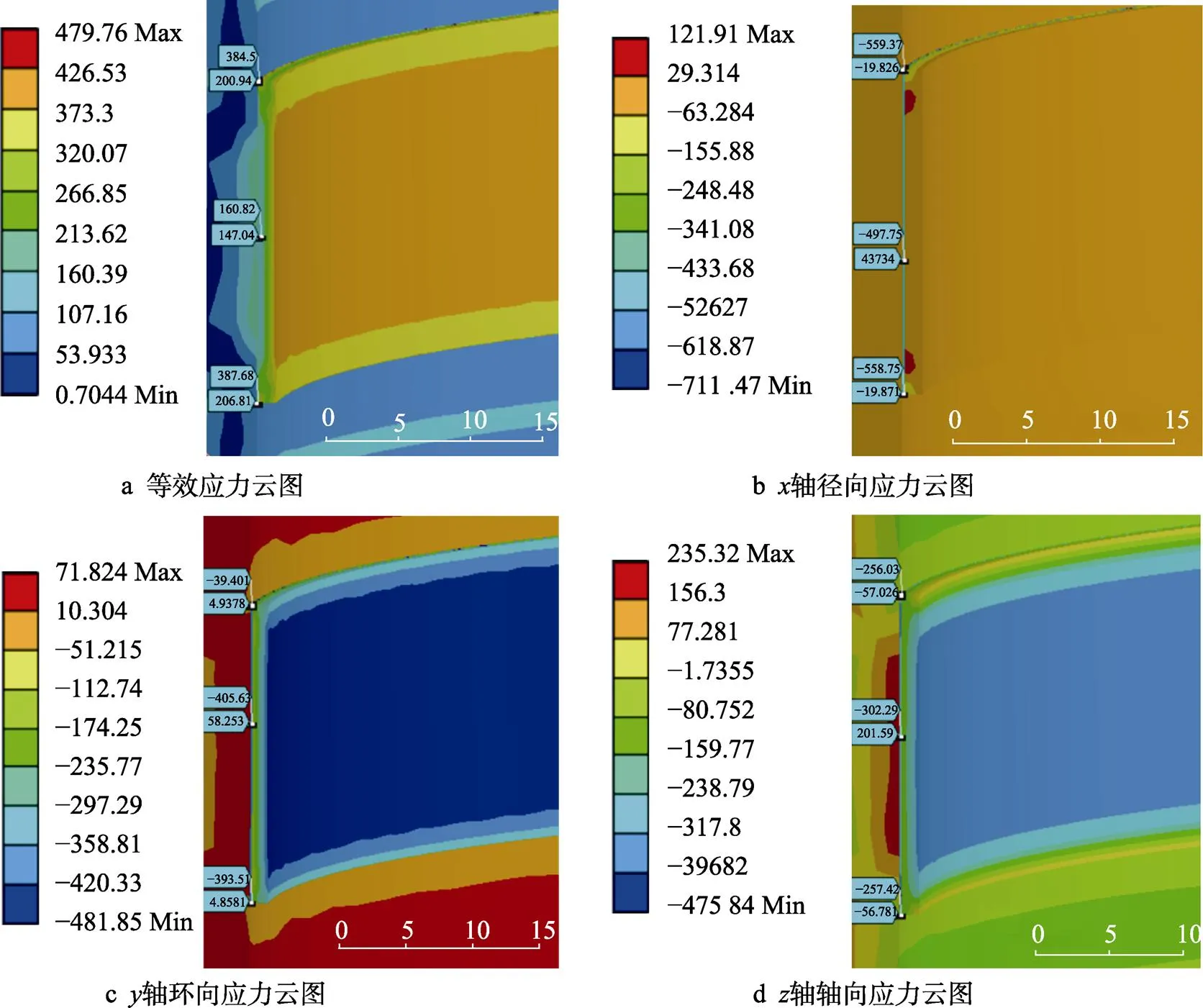
图15 预热温度为180 ℃下的应力场云图

图16为预热温度为200 ℃下的应力场云图。从图16a中可以看出，在预热温度为200 ℃时，最大等效应力分布相较于之前有了显著变化，位于黏结层和面层结合边缘处，达到515.84 MPa，面层表面应力约为458.58 MPa；从图16b中可以看出，沿轴径向方向，基体和部分涂层部位处于拉应力状态且应力分布均匀，最大拉应力位于黏结层和面层结合界面处达到118.19 MPa，最大压应力始终集中在黏结层和面层结合边缘处达到786.77 MPa；从图16c中可以看出，沿轴环向方向，涂层部分处于压应力状态且最大压应力分布相较于之前有了显著变化，位于黏结层和面层结合边缘处达到544.99 MPa，最大拉应力始终集中在基体处达到72.706 MPa；从图16d中可以看出，沿轴轴向方向，最大拉应力集中在基体和黏结层结合界面处达到236.4 MPa，应力以此界面为界限分别向基体和面层方向递减，到达基体表面时应力状态转变为压应力状态，到达黏结层和面层结合边缘处时达到最大压应力为539.47 MPa，面层表面应力值约为453.27 MPa。

首先，以各预热温度下的等效应力为研究对象，当基体进行30 ℃预热处理时，最大等效应力位于面层表面，随着基体预热温度的升高，面层表面最大等效应力分布范围逐渐减小，面层表面处应力值逐渐降低，当预热温度到达150 ℃以上时，最大等效应力分布从面层表面转移到黏结层和面层结合边缘处；随着基体预热温度升高，最大等效应力分布改变，数值变化趋势为先减小后增大。图17为在基体的不同预热温度下基体/黏结层/面层最大等效应力值，当预热温度从30 ℃提高到200 ℃时，最大等效应力值从576.66 MPa下降到453.09 MPa再上升到515.84 MPa；黏结层和面层结合边缘处最大等效应力值从220.58 MPa上升到515.84 MPa；面层表面处的等效应力值从576.66 MPa下降到390.53 MPa。最大等效应力集中在黏结层和面层结合边缘处有可能使其结合界面处萌生裂纹，并沿着界面或者平行于界面扩展，致使涂层分层或者翘曲失效[33]。为了更直观、清晰地对结果进行比较分析，将不同预预热温度下的最大等效应力值、分布位置列出，如表5所示。从表5中可以看出，最大等效应力在预热温度为150 ℃时取得最小值，预热温度低于150 ℃时，最大等效应力随预热温度升高而减小，应力集中部位位于面层表面；预热温度高于150 ℃时，应力值增加，应力集中部位转移到黏结层和面层结合边缘处。由此可以说明，预热温度在150 ℃时，基体/黏结层/面层系统等效应力值较小。

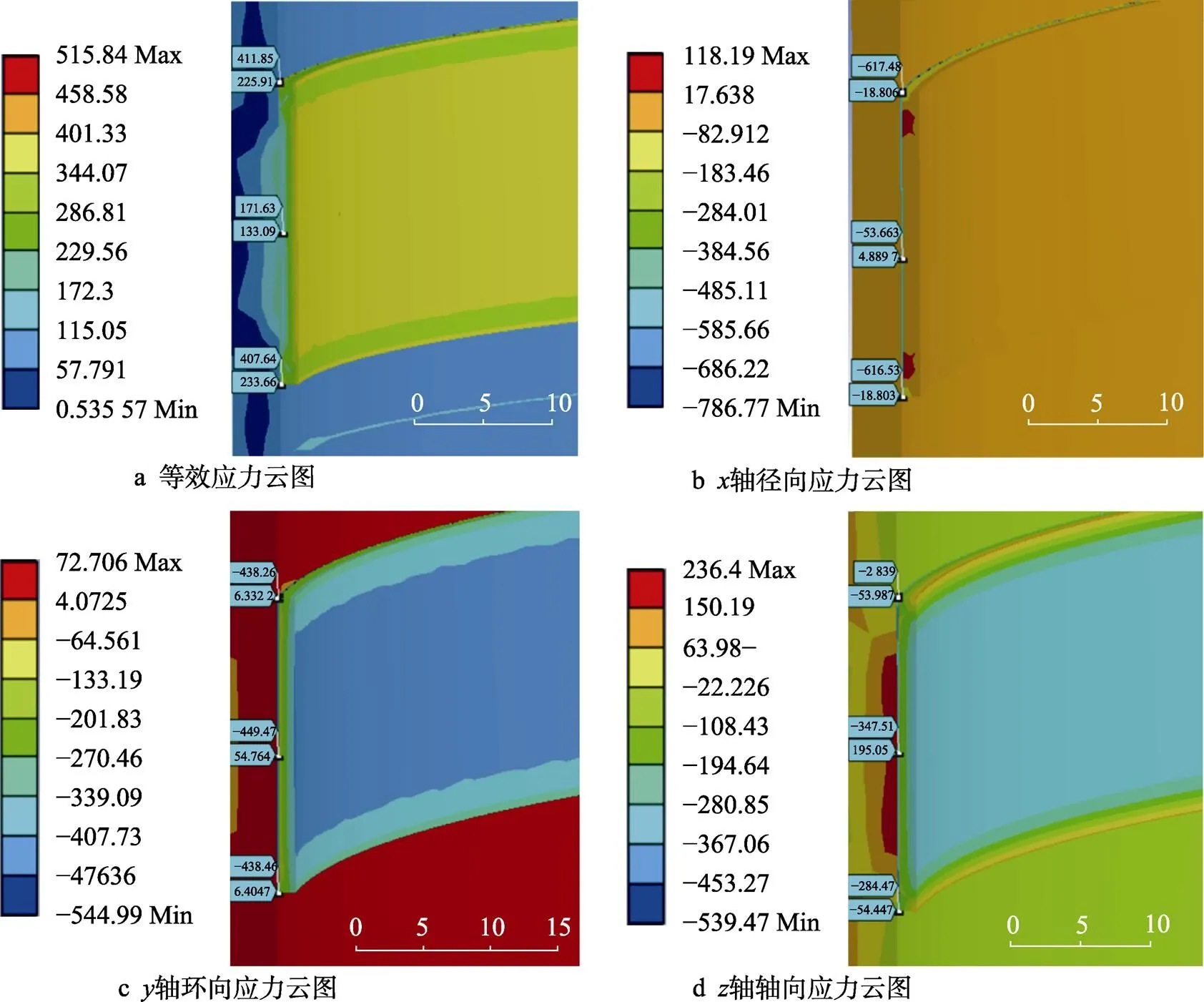
图16 预热温度为200 ℃下的应力场云图

图17 不同预热温度下基体/黏结层/面层最大等效应力值

以各预热温度下的轴径向应力为研究对象，由于径向应力是沿着半径方向的应力，故选取由面层上一点到基体上一点的连线为路径如图18所示，插入正应力（Normal Stress）命令，得到图19为不同预热温度下路径的径向应力分布图（图中的正值是拉伸应力，负值是压缩应力）。为了降低涂层剥离失效的概率，必须确保在涂层边缘的厚度方向上只有单一形式的残余应力。以0～1.35 mm的路径范围为研究对象，当基体预热温度为150～200 ℃时，路径范围内仅存压应力，其他温度条件下，该路径范围内拉应力和压应力均存在。与路径的其他区域相比，在1.1～1.3 mm的路径范围内存在较大的应力突变，以1.1 mm和 1.3 mm对应的曲线上的应力值为两个端点（图19中红色虚线部分），用两个端点连接的线段的斜率来表示路径上径向应力的突变。据计算，不同基体预热温度下的应力突变幅度和突变量如表6所示。当基体预热温度为150 ℃时，应力突变幅度为‒1 646.45 mpa/mm，应力突变值为‒329.29 mpa；当基体预热温度为180 ℃时，应力突变幅度为‒2 246.05 mpa/mm，应力突变值为‒449.21 mpa；当基体预热温度为200 ℃时，应力突变幅度为‒2 645.75 mpa/mm，应力突变值为‒529.15 mpa。与其他预热温度相比，当基体预热温度为150 ℃，涂层厚度方向的径向应力突变最小。综上所述，当基体预热温度为150 ℃时，涂层厚度方向的径向残余应力分布更加合理。

表5 最大等效应力及分布位置

Tab.5 Maximum equivalent stress and distribution position

note: S is the substrate, B is the bonding layer, T is the surface of the surface layer, and B/T is the bonding edge between the bonding layer and the surface layer.

以各预热温度下轴环向应力[34]为研究对象，当基体进行30 ℃预热处理时，基体处于拉应力状态，最大拉应力位于基体和部分黏结层处，黏结层边缘和面层处于压应力状态，最大压应力位于面层表面；随着基体预热温度的升高，基体始终处于拉应力状态，拉应力集中范围呈现先减小后增大；当基体预热温度达到180 ℃时，最大拉应力始终位于基体内部，最大压应力由面层表面转移至黏结层和面层结合边缘处，且最大压应力值呈现先减小后增大的趋势。图20为在基体不同预热温度下最大轴环向应力值（图中正值为拉应力，负值为压应力），当预热温度从30 ℃提高到200 ℃时，轴环向拉应力由65.212 MPa上升到72.706 MPa；轴环向压应力由608.2 MPa下降到481.85 MPa再上升到544.99 MPa。为了更直观、清晰地对结果进行比较分析，将不同预热温度下的轴环向最大拉应力值、最大压应力值和应力集中部位列出，如表7所示。环向应力是环绕着筒体方向，圆周切线方向的力，这种环向边缘拉应力和界面压应力会使界面边缘的微裂纹向界面中心区域扩展，最终导致涂层的分离失效[35]。从表7中可以看出，当预热温度为150～180 ℃时，轴环向应力取得较低水平拉应力和压应力；处于面层表面的压应力容易引发涂层弯曲变形，最大压应力集中在黏结层和面层结合边缘处容易使涂层间产生间隙导致涂层分离，因此，综合应力大小和应力分布两个因素来看，预热温度在150 ℃到180 ℃范围内时，涂层失效几率最小。

图18 面层到基体的路径示意图（图中1为起始点，2为终点）

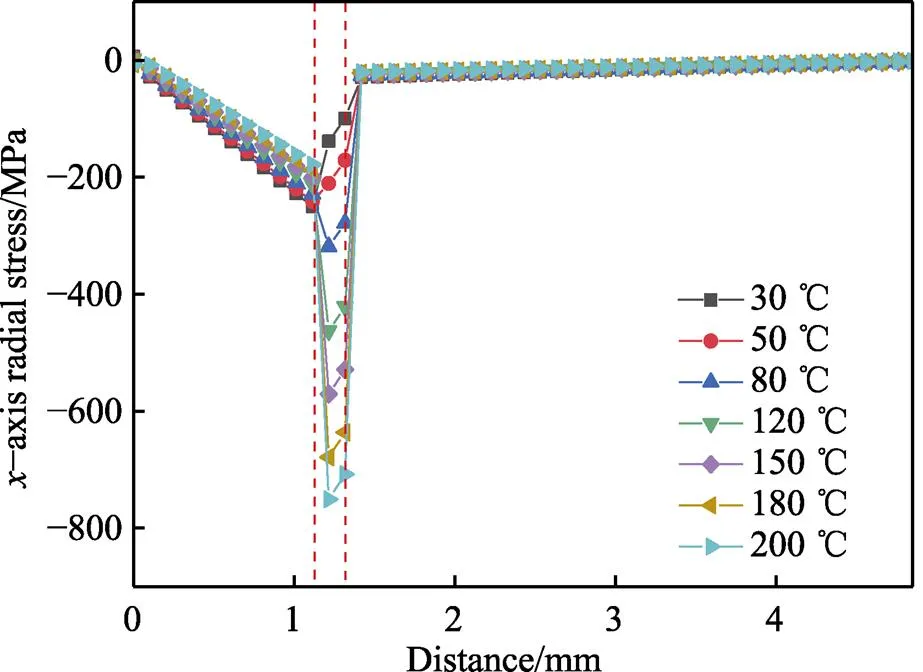
图19 不同预热温度下该路径的径向应力分布图

表6 预热温度120～200 ℃时轴径向应力突变

Tab.6 Sudden changes in axial residual stress of the path at a preheating temperature of 120 to 200 ℃

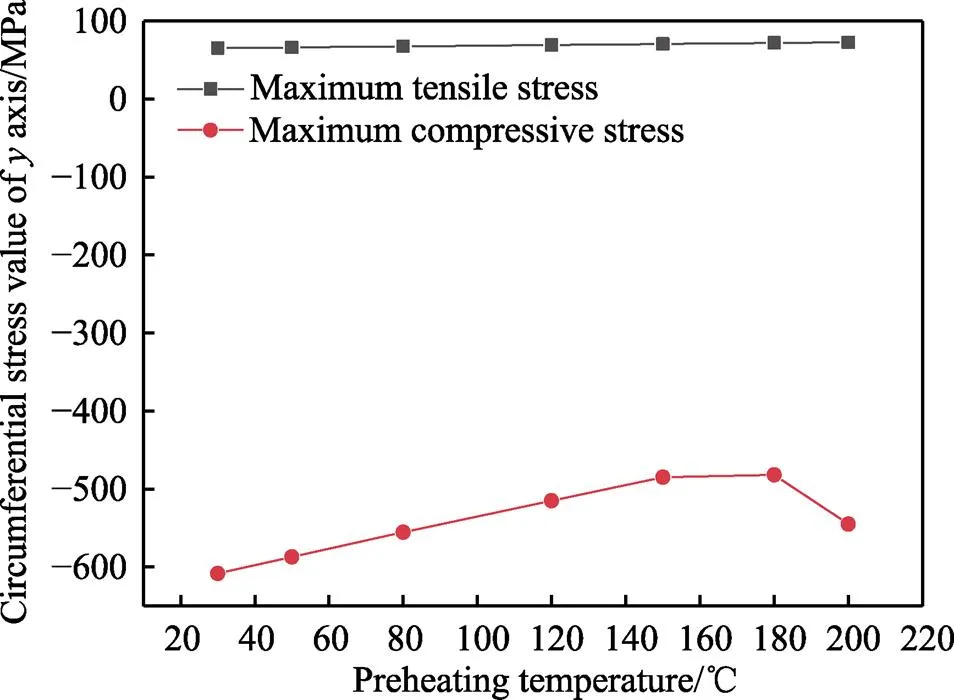
图20 基体不同预热温度下最大y轴环向应力值

表7轴环向最大拉应力/压应力及分布位置

Tab.7 Maximum tensile stress/compressive stress and distribution position in y-axis circumferential direction at different preheating temperatures of substrate

note: S is the matrix, S/B is the interface between the matrix and the bonding layer, B is the bonding layer, T is the surface of the surface layer, and B/T is the bonding edge between the bonding layer and the surface layer.

以各预热温度下轴轴向应力为研究对象，当基体进行30 ℃预热处理时，最大拉应力集中在基体和黏结层结合界面处，最大压应力集中在面层表面；随着预热温度的升高，位于基体和黏结层结合界面处的拉应力集中范围逐渐增大；当基体预热温度达到180 ℃时，最大压应力由面层表面逐渐转移到黏结层和面层结合边缘处，基体和黏结层结合界面处始终处于拉应力状态。图21为在基体不同预热温度下最大轴轴向应力值（图中正值为拉应力，负值为压应力），当预热温度从30 ℃提高到200 ℃时，轴轴向最大拉应力由229.53 MPa上升到236.4 MPa；轴轴向最大压应力由‒540.92 MPa下降到‒413.92 MPa再上升到‒539.47MPa。为了更直观、清晰地对结果进行比较分析，将不同预预热温度下的轴轴向最大拉应力值、最大压应力值和应力集中部位列出，如表8所示。轴向应力是垂直于涂层喷涂方向的纵向应力，这种轴向边缘拉应力和界面压应力会使界面边缘的微裂纹向界面中心区域扩展，最终导致涂层的分离失效。从表8中可以看出，当预热温度为150 ℃时，轴轴向应力取得最小压应力；处于面层表面的压应力容易引发涂层弯曲变形，最大压应力集中在黏结层和面层结合边缘处容易使涂层间产生间隙导致涂层分离，因此，综合应力大小和应力分布两个因素来看，预热温度在150 ℃时，涂层失效几率最小。

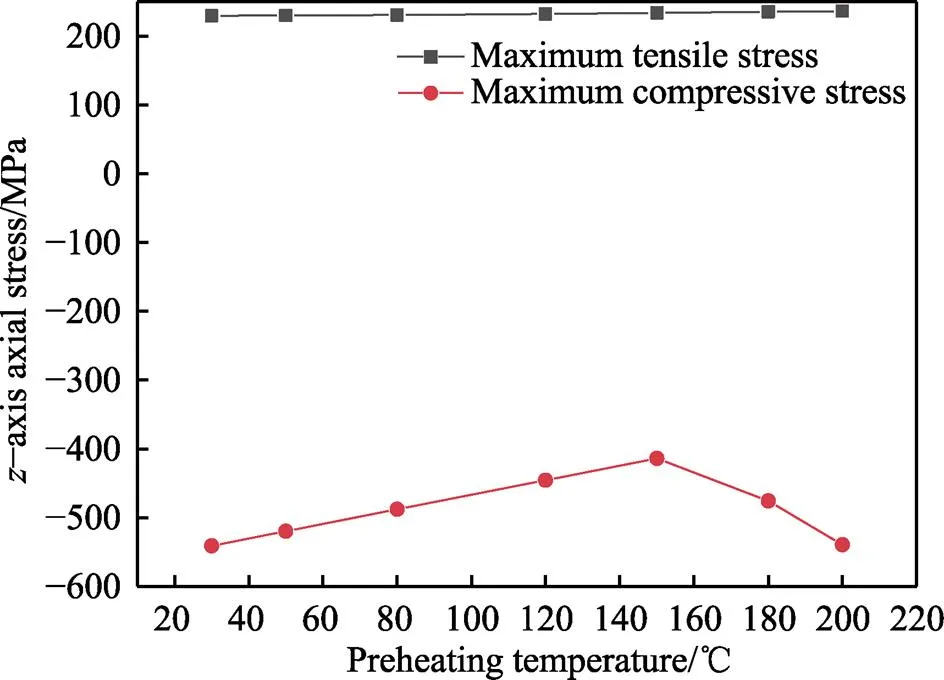
图21 基体不同预热温度下最大z轴轴向力值

表8轴轴向最大拉应力/压应力及分布位置

Tab.8 Maximum tensile stress/compressive stress and distribution position in z-axis direction at different preheating temperatures of substrate

note: S/B is the interface between the substrate and the bonding layer, T is the surface of the surface layer, and B/T is the bonding edge between the bonding layer and the surface layer.

3 结论

1）随着基体预热温度的升高，基体和涂层的温度梯度逐渐减小；最大等效应力值以预热温度150 ℃为界限先减小后增大，当预热温度小于150 ℃时，最大等效应力集中在面层表面；当预热温度大于150 ℃时，最大等效应力集中在黏结层和面层的结合边缘。

2）随着基体预热温度的升高，轴环向应力和轴轴向应力分布及变化趋势基本相同，最大拉应力变化不大，最大压应力值以预热温度150 ℃为界限先减小后增大，当预热温度小于150 ℃时，最大压应力集中在面层表面；当预热温度大于150 ℃时，最大压应力集中在黏结层和面层的结合边缘。

3）与轴环向应力和轴轴向应力相比，基体预热温度的变化对轴径向残余拉应力、径向残余压应力的分布位置影响更大。

4）根据涂层的残余应力的数值和分布位置的变化，基体预热温度应控制在150 ℃。

[1] 陈同灿, 丁坤英, 曹卫. 铝硅聚苯酯封严涂层的研究现状和发展[J]. 内燃机与配件, 2021(12): 35-37. CHEN Tong-can, DING Kun-ying, CAO Wei. The Status and Development of Sealing Coating on Aluminum Silicon Polyphenylene Easter[J]. Internal Combustion Engine & Parts, 2021(12): 35-37.

[2] 李荣锋, 李淦, 张书彦, 等. 残余应力对材料与装备制造失效影响的思考[J]. 物理测试, 2021, 39(6): 1-5. LI Rong-feng, LI Gan, ZHANG Shu-yan, et al. Cons­ideration of the Influence of Residual Stress on Material and Equipment Manufacturing Failure[J]. Physics Exam­ination and Testing, 2021, 39(6): 1-5.

[3] 渠志刚, 贺辛亥, 刘江南, 等. 基体预热温度对涂层表面形貌及残余应力影响的数值模拟[J]. 表面技术, 2017, 46(7): 57-64. QU Zhi-gang, HE Xin-hai, LIU Jiang-nan, et al. Nume­rical Simulation of Influence of Substrate Preheating Temperature on Coating Morphology and Residual Stress[J]. Surface Technology, 2017, 46(7): 57-64.

[4] PANG Ming, ZHANG Xiao-han, LIU Quan-xiu, et al. Effect of Preheating Temperature of the Substrate on Residual Stress of Mo/8YSZ Functionally Gradient Ther­mal Barrier Coatings Prepared by Plasma Spraying[J]. Surface and Coatings Technology, 2020, 385: 125377.

[5] LIU Hao, DU Xiao-tong, GUO Hua-feng, et al. Finite Element Analysis of Effects of Dynamic Preheating on Thermal Behavior of Multi-Track and Multi-Layer Laser Cladding[J]. Optik, 2021, 228: 166194.

[6] DENG Wen, AN Yu-long, HOU Guo-liang, et al. Effect of Substrate Preheating Treatment on the Microstructure and Ultrasonic Cavitation Erosion Behavior of Plasma- Sprayed YSZ Coatings[J]. Ultrasonics Sonochemistry, 2018, 46: 1-9.

[7] SADHU A, CHOUDHARY A, SARKAR S, et al. A Study on the Influence of Substrate Pre-Heating on Mitigation of Cracks in Direct Metal Laser Deposition of NiCr­SiBC-60%WC Ceramic Coating on Inconel 718[J]. Surface and Coatings Technology, 2020, 389: 125646.

[8] XIE Ying-chun, PLANCHE M P, RAOELISON R, et al. Investigation on the Influence of Particle Preheating Temperature on Bonding of Cold-Sprayed Nickel Coatings[J]. Surface and Coatings Technology, 2017, 318: 99-105.

[9] YU M, LI W Y, WANG F F, et al. Effect of Particle and Substrate Preheating on Particle Deformation Behavior in Cold Spraying[J]. Surface and Coatings Technology, 2013, 220: 174-178.

[10] REZVANI RAD M, FARRAHI G H, AZADI M, et al. Effects of Preheating Temperature and Cooling Rate on Two-Step Residual Stress in Thermal Barrier Coatings Considering Real Roughness and Porosity Effect[J]. Ceramics International, 2014, 40(10): 15925-15940.

[11] 侯平均, 王汉功, 汪刘应, 等. 等离子喷涂双层热障涂层沉积过程的数值模拟[J]. 焊接学报, 2009, 30(11): 97-100, 104, 118. HOU Ping-jun, WANG Han-gong, WANG Liu-ying, et al. Numerical Simulation on Deposition Process of Duplex Thermal Barrier Coating by Plasma Spraying[J]. Transactions of the China Welding Institution, 2009, 30(11): 97-100, 104, 118.

[12] MUHAMMAD A, ALI M A H, SHANONO I H. ANSYS-a Bibliometric Study[J]. Materials Today: Proce­edings, 2020, 26: 1005-1009.

[13] SUN Fu-zhen, LI Yan, TAN Wen-dan, et al. Effect of Laser Scanning Speed on the Thermal-Mechanical Coupling Field of Laser Remelting of Valve Seat[J]. Optik, 2021, 225: 165776.

[14] 李延平, 赵万华, 卢秉恒. 热喷涂涂层和基体中残余应力预报与控制研究[J]. 工程力学, 2005, 22(5): 236-240. LI Yan-ping, ZHAO Wan-hua, LU Bing-heng. Prediction and Control of Residual Stresses in Thermal Sprayed Coatings[J]. Engineering Mechanics, 2005, 22(5): 236- 240.

[15] 渠志刚. 等离子喷涂涂层表面形貌及残余应力的数值模拟[D]. 西安: 西安工程大学, 2017. QU Zhi-gang. Numerical Simulation of Plasma Spray Coating Surface Morphology and Residual Stress[D]. Xi'an: Xi'an Polytechnic University, 2017.

[16] 赵娇玉. 热喷涂涂层残余应力产生及控制因素研究[D]. 沈阳: 沈阳工业大学, 2009. ZHAO Jiao-yu. Study on the Formation of Residual Stress in Thernal Spray Coatings and Its Controlling Factors[D]. Shenyang: Shenyang University of Technology, 2009.

[17] WANG L, WANG Y, SUN X G, et al. Finite Element Simulation of Residual Stress of Double-Ceramic-Layer La2Zr2O7/8YSZ Thermal Barrier Coatings Using Birth and Death Element Technique[J]. Computational Mater­ials Science, 2012, 53(1): 117-127.

[18] TSUI Y C, CLYNE T W. An Analytical Model for Predicting Residual Stresses in Progressively Deposited Coatings Part 1: Planar Geometry[J]. Thin Solid Films, 1997, 306(1): 23-33.

[19] 宣海军, 陆晓, 洪伟荣, 等. 航空发动机机匣包容性研究综述[J]. 航空动力学报, 2010, 25(8): 1860-1870. XUAN Hai-jun, LU Xiao, HONG Wei-rong, et al. Review of Aero-Engine Case Containment Research[J]. Journal of Aerospace Power, 2010, 25(8): 1860-1870.

[20] PATIL A S, MOHEIMANI R, DALIR H. Thermom­echanical Analysis of Composite Plates Curing Process Using ANSYS Composite Cure Simulation[J]. Thermal Science and Engineering Progress, 2019, 14: 100419.

[21] 黄静, 马原, 王明杰, 等. 精密铸造0Cr17Ni4Cu3Nb不锈钢航空发动机零件[J]. 特种铸造及有色合金, 2019, 39(2): 159-162. HUANG Jing, MA Yuan, WANG Ming-jie, et al. Investigation and Optimization of Investment Casting 0Cr17Ni4Cu3Nb Stainless Steel Parts of Aero-Engines[J]. Special Casting & Nonferrous Alloys, 2019, 39(2): 159-162.

[22] 尹瀛月. 平面等离子喷涂TiO2涂层数值模拟基础研究[D]. 乌鲁木齐: 新疆大学, 2017. YIN Ying-yue. Basic Research on Numerical Simulation of Planar Plasmasprayed TiO2Coating[D]. Urumqi: Xinjiang University, 2017.

[23] 赵诚. 铝钢钎焊与黏接光纤传感监测的试验及模拟[D]. 南昌: 南昌大学, 2015. ZHAO Cheng. Monitoring Experiment and Simulation for Brazing and Bonding of Aluminum Alloy and Steel Based on Optical Fiber Sensing Technology[D]. Nanchang: Nanchang University, 2015.

[24] Ahmed F, Christopher C, Bernd t, et al. Numerical Modelling of Particle Impact and Residual Stresses in Cold Sprayed Coatings: A review[J] Surface and Coatings Technology, 2021, 409: 126835-126835.

[25] 段淇耀. 针对多层复合材料热物性参数测试方法的研究[D].哈尔滨: 哈尔滨工业大学, 2019. DUAN Qi-yao. Research on Testing Method of Thermophysical Properties of Multilayer Composites[D]. Harbin: Harbin Industrial University, 2019.

[26] 董珍一, 林莉, 雷明凯, 等. 基于BPNN的封严涂层孔隙分布均匀性超声表征[J]. 航空学报, 2022, 43(5): 425294. DONG Zhen-yi, LIN Li, LEI Ming-kai, et al. Ultrasonic Quantitative Characterization of Pore Distribution Unifo­rmity of Seal Coating Based on BPNN[J]. Acta Aeron­autica et Astronautica Sinica, 2022, 43(5): 425294.

[27] WEI Zhi-yuan, CAI Hong-neng, TAHIR A, et al. Stress States in Plasma-Sprayed Thermal Barrier Coatings Upon Temperature Cycling: Combined Effects of Creep, Plastic Deformation, and TGO Growth[J]. Ceramics Internat­ional, 2019, 45(16): 19829-19844.

[28] TILLMANN W, KHALIL O, BAUMANN I. Influence of Spray Gun Parameters on Inflight Particle's Charac­teristics, the Splat-Type Distribution, and Microstructure of Plasma-Sprayed YSZ Coatings[J]. Surface and Coatings Technology, 2021, 406: 126705.

[29] 孙越, 张兆林, 刘欣, 等. 激光熔覆多层涂层温度场的数值模拟[J]. 电焊机, 2021, 51(5): 61-65, 117. SUN Yue, ZHANG Zhao-lin, LIU Xin, et al. Numerical Simulation of Temperature Field in Multilayer Laser Cladding[J]. Electric Welding Machine, 2021, 51(5): 61-65, 117.

[30] 吴俊杰, 朱振杰, 孙德鹏, 等. 基于热力耦合的轴承失效分析[J]. 组合机床与自动化加工技术, 2021(6): 42-44, 58. WU Jun-jie, ZHU Zhen-jie, SUN De-peng, et al. Failure Analysis of the Bearing Based on the Thermo-Mechanical Coupling[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(6): 42-44, 58.

[31] 李建军, 彭谦之, 贾贝, 等. 基于数值仿真的TC4合金锻前加热工艺参数研究[J]. 特种铸造及有色合金, 2021, 41(7): 890-895. LI Jian-jun, PENG Qian-zhi, JIA Bei, et al. Heating Process Parameters of TC4 Alloy before Forging Based on Numerical Simulation[J]. Special Casting & Nonfe­rrous Alloys, 2021, 41(7): 890-895.

[32] 陈远远. ANSYS软件在材料力学弯曲正应力教学中的运用[J]. 河南教育(高教), 2019(7): 98-100. CHEN Yuan-yuan. Application of ANSYS Software in the Teaching of Bending Normal Stress of Material Mecha­nics[J]. Henan Education, 2019(7): 98-100.

[33] 姜祎, 徐滨士, 王海斗. 热喷涂层残余应力的来源及其失效形式[J]. 金属热处理, 2007, 32(1): 25-27. JIANG Yi, XU Bin-shi, WANG Hai-dou. Sources and Failure Modes of Residual Stresses in Thermal Sprayed Coatings[J]. Heat Treatment of Metals, 2007, 32(1): 25-27.

[34] 李世亚, 向思杰, 吴树航, 等. 高桩码头变壁厚钢管桩环向焊缝应力集中系数研究[J]. 港工技术, 2021, 58(4): 58-61. LI Shi-ya, XIANG Si-jie, WU Shu-hang, et al. Study on Stress Concentration Coefficient at Circumferential Weld Seam of Steel Pipe Piles with Variable Wall Thickness for High Piled Berth[J]. Port Engineering Technology, 2021, 58(4): 58-61.

[35] 田甜. 等离子喷涂8YSZ热障涂层沉积过程累积应力的数值模拟[D]. 福州: 福州大学, 2013: 29-31. TIAN Tian. Simulation of Stress Accumulation in Plasma Sprayed 8YSZ TBCs during the Deposition[D]. Fuzhou: Fuzhou University, 2013: 29-31.

Effect of Substrate Preheating Temperature on Residual Stress of Aluminum-Silicon Abrasion-Sealing Coatings by Plasma Spraying

,*,,

(School of Material Science and Engineering, Nanchang Hangkong University, Nanchang 330063, china)

As a wearable sealing coating, the Al-Si alloy coating has the advantages of low surface roughness, no chipping during coating operation, and the more polished the coating is, the smoother it will become. However, there are few reports on the finite element analysis of the Al-Si alloy sealing coating. Al-Si sealing coatings of the cartridge receiver are sprayed by plasma spraying as the spraying technology. During the coating spraying process, there will be sudden heating and cooling, so it is easy to generate residual stress on the machined workpiece and coating during spraying. The coating residual stress is one of the main reasons for the cracking and peeling of the Al-Si coating, so it is very important to reduce the coating residual stress. Before plasma spraying, the substrate needs to be preheated. Optimize the preheating temperature of the substrate, which can reduce the cooling rate of the droplets, improve the uniformity of the temperature distribution of the coating system, reduce the thermal stress of the coating, and thus reduce the residual stress of the coating. Therefore, it is necessary to determine an optimal preheating temperature of the substrate to improve the effect of residual stress on the coating stability.

Based on the thermal elastic plastic finite element theory and ANSYSWORKBENCH finite element analysis software, this paper establishes a double-layer coating model, uses the indirect thermal mechanical coupling method to study the effect of different substrate preheating temperatures on the residual stress and distribution of Al-Si coating, and analyzes the value and distribution of the equivalent stress,-axis radial stress,-axis circumferential stress, and-axis axial stress of the surface layer/bonding layer/substrate system. The purpose is to find the best preheating temperature of the substrate for spraying Al-Si coating. It can be found that when the preheating temperature is lower than 150 ℃, the maximum equivalent stress decreases with the increasing preheating temperature, and the stress concentration is located on the surface of the surface layer; When the preheating temperature is higher than 150 ℃, the stress value increases, and the stress concentration part is transferred to the bonding edge of bonding layer and the surface layer. Compared with other preheating temperatures, when the substrate preheating temperature is 150 ℃, the radial stress mutation in the coating thickness direction is minimum. When the preheating temperature is 150 ℃ to 180 ℃, the-axis circumferential stress achieves low horizontal tensile stress and compressive stress. The compressive stress on the surface of the surface layer is easy to cause bending deformation of the coating. The maximum compressive stress concentrate at the bonding edge of the bonding layer and the surface layer is easy to cause gaps between the coatings and lead to coating separation. For the-axis circumferential stress, the coating failure probability is minimum when the preheating temperature is 150 ℃ to 180 ℃. With the increase of preheating temperature, the distribution and change trend of shaft circumferential stress and-axis axial stress are basically the same. Compared with-axis circumferential stress and-axis axial stress, the change of substrate preheating temperature has greater effect on-axis radial tensile stress and radial compressive stress. It can be concluded that the preheating temperature of the substrate should be controlled at 150 ℃ when plasma spraying Al-Si wearable sealing coating.

aluminum silicon abrasion coating; preheating temperature; stress field; numerical simulation

2022-10-20；

2023-02-18

tg174.442

A

1001-3660(2023)10-0335-15

10.16490/j.cnki.issn.1001-3660.2023.10.029

2022-10-20；

2023-02-18

江西省自然科学基金项目（20202BABL204006）；南昌航空大学基金（EA201801211）

Supported by Natural Science Foundation of Jiangxi Province (20202BABL204006); Nanchang Hangkong University Foundation, China (EA201801211)

苏宇航, 温祯洪, 罗军明, 等.预热温度对机匣等离子喷涂铝硅可磨耗封严涂层应力场影响的数值模拟[J]. 表面技术, 2023, 52(10): 335-349.

SU Yu-hang, WEN Zhen-hong, LUO Jun-ming, et al. Effect of Substrate Preheating Temperature on Residual Stress of Aluminum-Silicon Abrasion-Sealing Coatings by Plasma Spraying[J]. Surface Technology, 2023, 52(10): 335-349.

通信作者（Corresponding author）

责任编辑：万长清