超音速火焰喷涂镍基涂层颗粒沉积特性的数值模拟

许耀飞，刘思思，杨正航，姜胜强，刘金刚

热喷涂与冷喷涂技术

超音速火焰喷涂镍基涂层颗粒沉积特性的数值模拟

许耀飞，刘思思*，杨正航，姜胜强，刘金刚

（湘潭大学 机械工程学院，湖南 湘潭 411105）

考虑后续不同粒径颗粒随机冲击的影响，探索热喷涂涂层颗粒的沉积特性。利用ABAQUS建立颗粒与基底冲击模型，通过颗粒冲击的凹坑深度和应力分布进行网格收敛性研究。通过实验验证模型的可行性。随后，应用验证模型研究颗粒以不同入射角和速度冲击基底时的沉积特性，以及4个颗粒重叠冲击基底及多颗粒随机冲击基底表面时的沉积特性。在颗粒入射角从15°增至60°时，颗粒更好地附着于基底表面；当颗粒速度从350 m/s增至500 m/s时发生了溅射现象，可能造成绝热剪切失稳现象，形成有效结合；在4个颗粒冲击基底时，第2个颗粒对第1个颗粒及基底的影响都最明显；当多颗粒随机冲击基底时，在后续颗粒的冲击和沉积作用下，填充颗粒的形状不规则，同时第1层颗粒可能与基底形成机械咬合。在超音速火焰喷涂时应当倾斜一定角度，同时提升颗粒速度，这对制备涂层更有利；在颗粒重叠冲击时，后续颗粒增大了第1个颗粒的压缩效果，且更深入地嵌入不锈钢基底，这有利于颗粒与颗粒之间的后续黏结；当多颗粒随机冲击基底时，在第1层沉积颗粒与基底之间，以及涂层内相邻颗粒之间均观察到高塑性应变，表明涂层出现黏结，同时后期沉积的颗粒未完整压缩变形。

超音速火焰喷涂；机械咬合；多颗粒；重叠冲击；ABAQUS模拟

超音速火焰喷涂（HVOF）是一种比较成熟且先进的热喷涂技术，广泛应用于航空航天、石油化工和车辆船舶等领域[1-3]。由于镍基粉末材料具有优异的耐磨性、耐腐蚀性、经济性等，被广泛用于航空喷气发动机、工业燃气轮机等的热端部件的制造[4]。其中，采用HVOF制备镍基涂层成为表面防护领域的研究热点[5-7]。研究表明[8]，HVOF制备涂层的本质是粉末颗粒在基底材料表面沉积时压缩堆积成形的过程，因此研究涂层颗粒的沉积特性对于提高涂层质量具有重要意义[9]。

针对喷涂颗粒的沉积变形特性，Zang等[10]运用ABAQUS研究了入射角对颗粒冲击基底的影响，结果表明，入射角越大，颗粒沉积基底表面凹坑越深。Khamsepour等[11]采用仿真方法，研究了Ti-6Al-4V颗粒在不同初始速度下颗粒变形量的变化情况，结果表明，速度越高，动能越大，颗粒在冲击后的瞬间温度变高，从而有利于Ti-6Al-4V颗粒附着于基底。Astaraee等[12]使用CEL方法研究了单个Cu颗粒以不同速度冲击PEEK，结果表明，速度越高，则基底冲击深度越大，温度越高，塑性应变越大，在冲击过程中颗粒还会发生回弹现象。Che等[13]通过聚合物基底上Cu颗粒的单颗粒冲击试验，探索了第1层涂层的形成，结果表明，影响金属和聚合物基材之间键合的2个主要参数是速度和温度。Song等[14]使用CEL框架创建了一个多颗粒碰撞模型，以预测金属喷涂过程中的孔隙率，并进行了网格收敛研究，结合试验结果验证了多颗粒模型的正确性。

总体来说，数值模拟方法可以直观地反映颗粒与基底接触界面上的温度及应变的变化情况，为证明热喷涂高速碰撞过程中界面局部熔化的发生提供了可靠的依据。另外，随着数值研究工作的不断深入，研究重点已经不局限于单个颗粒与基底的碰撞变形行为，更多的注意力开始转向多颗粒冲击过程的数值模拟，通过多颗粒冲击数值模拟可以研究冲击过程中温度和变形的累积效应，更加符合实际喷涂工作，有助于更好地了解涂层的沉积机理。本文在前期的基础上研究单个颗粒以不同入射角和速度冲击基底时的沉积特性，并进一步研究4个颗粒连续重叠冲击基底及多颗粒随机冲击基底表面时的沉积特性。

1 材料与方法

1.1 有限元模型

在ABAQUS中，建立镍颗粒、304不锈钢基底模型。由于镍颗粒会出现较大变形，因此在研究过程中采用CEL耦合方法对颗粒和基底进行建模，如图1所示。在图1a～c这些模型中，基底模型为直径300 μm、高度150 μm的圆柱体，颗粒直径为30 μm。在图1d～e中，模型为100个20～70 μm不等的颗粒，基底模型的长度、宽度、高度均为700 μm。为了避免应力波在模型边界反射时引起数值的不稳定[15]，将颗粒的建模直径设置为远小于基底直径。在基板中创建不同的分区，从而在非冲击区域获得优化的网格分布。在颗粒与基底接触区域进行网格细化，采用过渡网格法对基底进行网格划分，从而降低计算成本，确保计算精度，如图2所示。将颗粒与基底的接触设置为通用接触，摩擦因数为0.3。在不模拟颗粒入射角对沉积特性的影响的情况下，对基底的底面施加全约束，对颗粒与基底的、面施加面对称约束，其余表面均设置为自由状态，限定颗粒仅能垂直于金属基底表面喷涂路径运动。在计算过程中，颗粒与基底的冲击时间根据最远颗粒到达基底充分变形时来粗略估计[16]。同时，假设颗粒与基底之间绝热[16]。前面建模选用20～70 μm的颗粒，这是根据激光粉末分析仪测量粒度分布所得，如图3a所示。粒度的累积概率分布由对数正态函数估计，见式（1）。

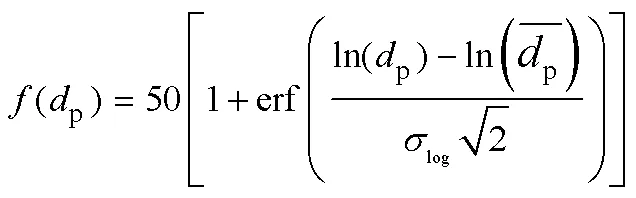
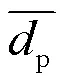
根据热喷涂中使用的粉末材料，可以测出颗粒的粒度分布曲线。在粒度分布曲线中，平均粒径是粒度分布曲线中累积分布为50%时最大颗粒的等效直径。70、50和20分别表示粒度分布曲线中累积分布为70%、50%、20%时最大颗粒的等效直径。在确定多颗粒冲击模型中颗粒的粒径范围时，由于20～70之外的颗粒在整个粉末中的占比较小，所以可以忽略两者之外的粒径。将选择范围内的粒径按照相同间隔取几组直径相同的颗粒，然后根据粒径粒度的累积概率分布估算不同粒径的颗粒数量，总体为100个，如图3b所示。多颗粒碰撞条件通过多颗粒随机碰撞模拟的计算流体动力学确定[17]，如图3c～e所示。

1.2 材料模型

采用Johnson-Cook塑性模型描述镍颗粒和304不锈钢基底，该模型考虑了颗粒沉积过程中的应变强化、升温熔化、摩擦，以及塑性功与热能之间的转化。应力用von Mises塑性模型来表示。材料的屈服应力的计算见式（2）[18]。

图1 有限元沉积模型

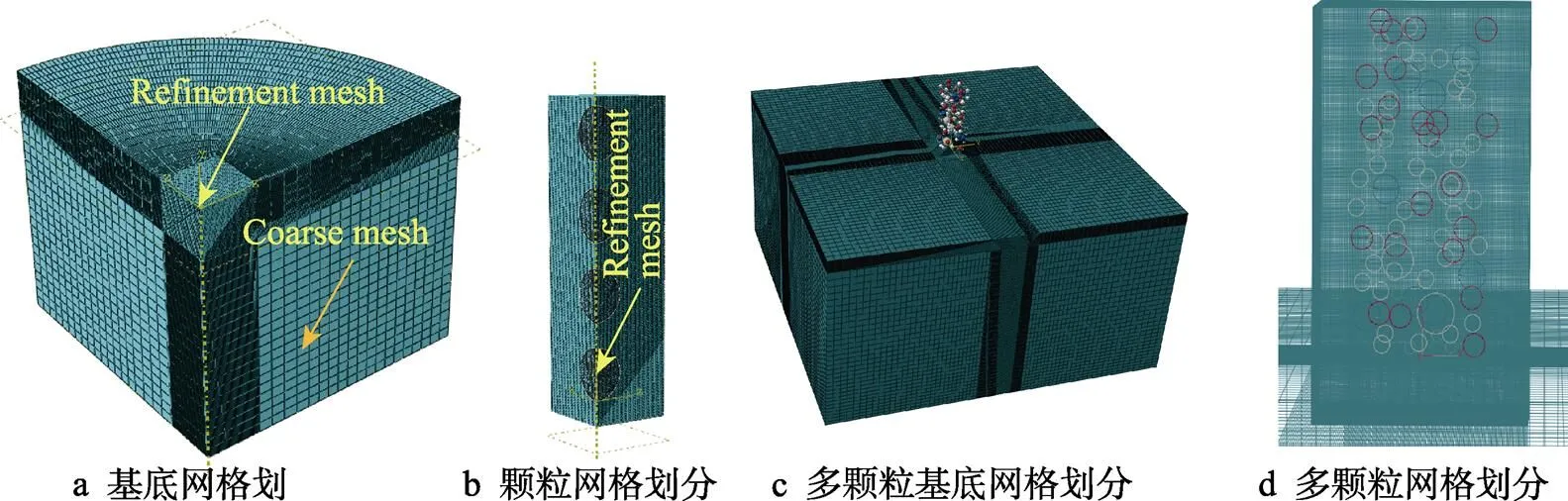
图2 模型网格划分示意图

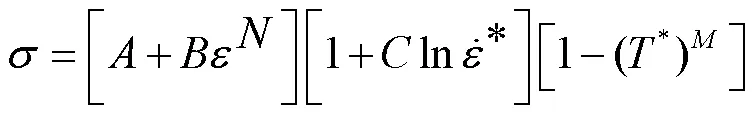
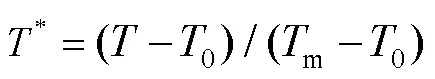
式中：为材料的温度；0为材料的参考温度；m为材料的熔化温度。

弹性行为采用线性Mie-GrÜneisen状态方程描述，其力学性能和热性能假定为各向同性。颗粒和基底材料的特性参数如表1所示[19-20]。

1.3 网格独立性测试

在数值模拟中，使用更精细的网格会产生更精确的结果，但代价是计算成本较高。这里进行了系统的网格独立性测试，以获得合理的网格尺寸，确保精度，同时保证合理的计算成本。在选择优化网格时，考虑了SVANG Mises应力和最大沉积深度[10]，如表2、图4所示。在网格独立性测试中，考虑了5种网格尺寸（表2），对于试验1～3，变形附近的应力（SVANG Mises）为803～880 MPa，存在显著偏差，结合图4可看出这是由网格粗糙所致。试验4、5中的应力（SVANG Mises）分别为888.2、890.2 MPa，结合图4可看出应力分布相似。对于试验1～3，目标材料的深度逐渐增大，试验4、5的深度分别为2.11、2.07 μm，非常接近。当元素数量为1 589 240（试验4）时，应力（SVANG Mises）和渗透的变化很小，表明计算结果对网格数不敏感。由于试验5的计算成本大大超过了其他网格尺寸，因此模型中采用试验4。

表1 镍颗粒和304不锈钢材料的特性参数

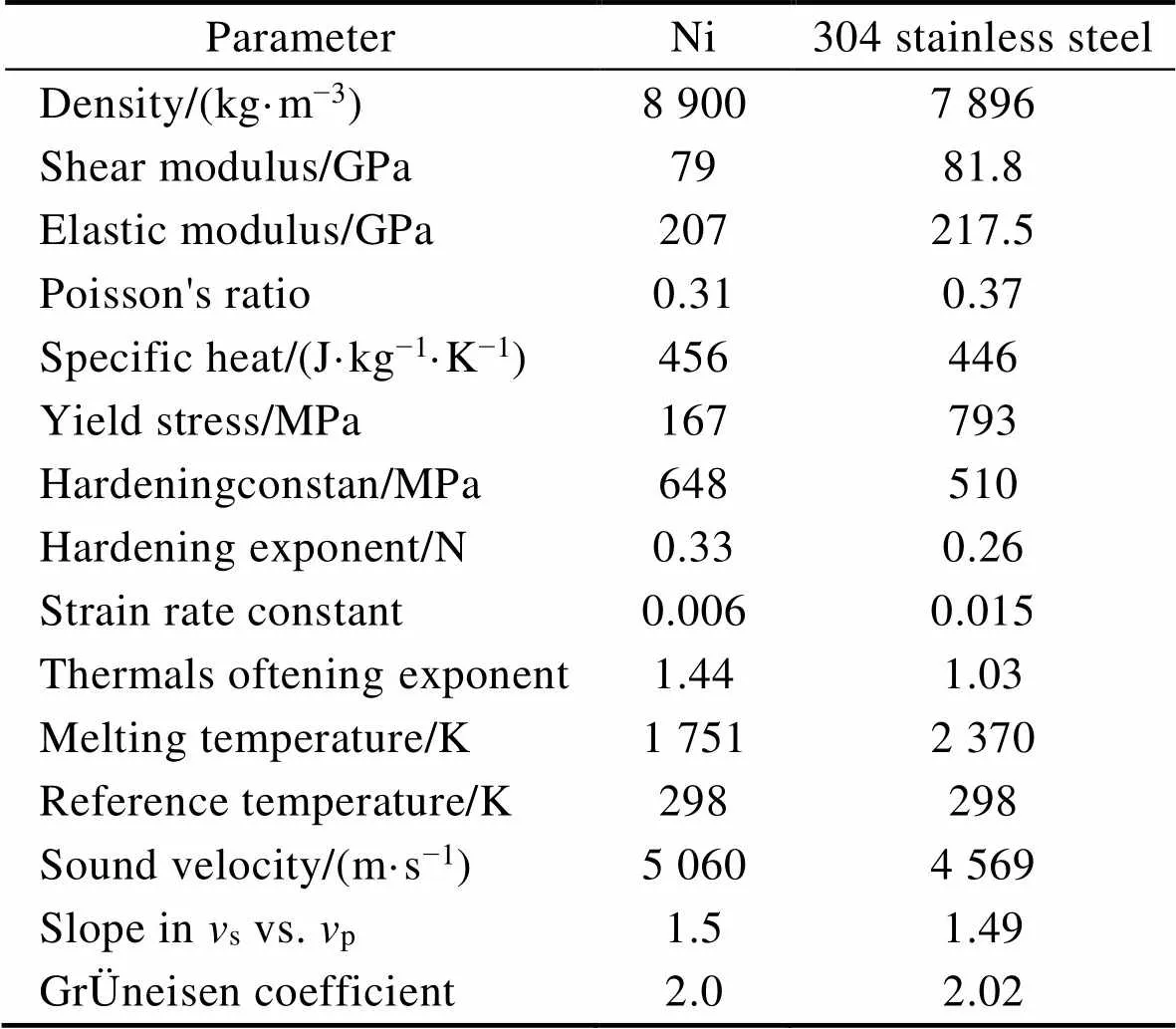
Tab.1 Ni particles and 304 stainless steel material feature parameters

表2 网格收敛测试中使用的参数

Tab.2 Parameters used in mesh convergence test

图4 不同网格尺寸的最大应力、最大沉积深度曲线和最大应力分布

1.4 实验验证

为了验证上述网格质量和模型的可靠度，这里通过文献已有的SEM图[21]与模拟塑性应变云图进行对比（如图5a所示），20 μm的镍颗粒的撞击变形规律与实际过程颗粒变形规律基本保持一致，塑性应变最高达到1.829 MPa，且具有回弹效果。同时，颗粒和基底的塑性变形区主要集中在二者的接触面附近此外，由于颗粒的质量较小，碰撞时的能量较小，造成基底的塑性变形有限，且撞击前的速度较高，但回弹力较大，从而导致与基底的有效结合面积较小。如图5b所示，40 µm的镍颗粒在冲击基底后的塑性云图与实际颗粒变形规律也基本保持一致，塑性应变最高达到2.226 MPa。由于颗粒的尺寸更大，增大了碰撞能量，使得基底产生了更大的塑性变形，颗粒与基底结合良好，颗粒的扁平化过程得以延长。通过对比形貌和现象可知，其网格质量及模型可行。

图5 不同粒径颗粒冲击后SEM形貌与等效塑性应变云图

2 结果与讨论

2.1 颗粒沉积过程中的变形特性

超音速火焰喷涂的颗粒速度一般为300～500 m/s，颗粒温度可达800～1 600 K[22-23]。同时，沉积在基底表面的颗粒通常利用颗粒的压缩率和沉积深度来表征颗粒的变形程度和喷涂效果，具体如图6所示。定义颗粒的压缩率，见式（4）。定义颗粒的沉积坑深度，见式（5）。

=(c−z)/c(4)

式中：c为颗粒的初始高度，即颗粒直径；z为颗粒变形后的高度。

=1−2(5)

式中：以基底底面为基准面，1为基底表面高度；2为沉积坑最深处的高度。

为了研究颗粒沉积过程中的变形行为，选取实验常用的15～45 μm范围内的中径颗粒（30 μm）进行模拟。在速度为450 m/s、初始温度为800 K、基底温度为298 K的初始条件下，不同时刻沉积的等效塑性应变云图如图7所示。颗粒在冲击基体后立即开始变形，将颗粒下半部分压缩的材料推向基体两端，基体发生的变形较小，只有较浅的沉积坑。颗粒变形区域主要集中在颗粒与基体的接触区周围。随着颗粒冲击的进行，颗粒的等效塑性应变逐渐增大。在21 ns时，颗粒边缘不断扩展，颗粒内部材料开始向外溢出，增大了颗粒与基体的结合面积。在42 ns时，颗粒变形明显，沉积坑的宽度和深度同时增加，以配合颗粒的变形。在60 ns时，镍颗粒被压缩成明显的扁平状，颗粒嵌入基体的冲击凹坑中，该凹坑边缘稍微向上凸起。

如图8a所示，描述了颗粒的动态沉积深度和压缩率。在前15 ns内，颗粒一直处于穿透过程，在21 ns时达到最大沉积深度（2.11 μm）。在22～60 ns内，颗粒处于反弹阶段，缓慢向上弹起，但未脱离基体。采用CEL方法时，颗粒冲击基底一般被设置为通用接触，所以颗粒会发生反弹现象[12,24-25]。此外，在42 ns时，颗粒的压缩率升至一个较大值，随着时间的推移，在42～60 ns内压缩率的变化趋势变缓。在60 ns时，颗粒压缩率为0.57左右。在高速冲击下，基体与颗粒的温度都迅速上升，如图8b所示。颗粒温度一开始持续上升是因为在冲击过程中，颗粒的近基体端首先与基体接触，随着颗粒的持续冲击，颗粒的变形增大，颗粒被绝热压缩，将被压缩材料推向颗粒边缘，产生了较大的塑性变形，因此颗粒与不锈钢基体接触界面区域的温度迅速升高。由于颗粒的塑性变形大于基体，因此温度上升得更快。温度在42 ns后基本恒定，出现这种现象说明随着颗粒冲击动能的减小，塑性耗散也随之减小，因此温度基本恒定。基体温度在21 ns时上升得最快，随后在短时间内保持恒定，这是因为在21 ns时沉积深度达到最大值。此时，基体变形得最强烈，变形能转化为热能，温度升至最大值。在21 ns后，颗粒缓慢反弹，不再继续穿透，温度基本保持恒定。

图6 压缩率与沉积深度示意图

图7 镍颗粒动态沉积过程

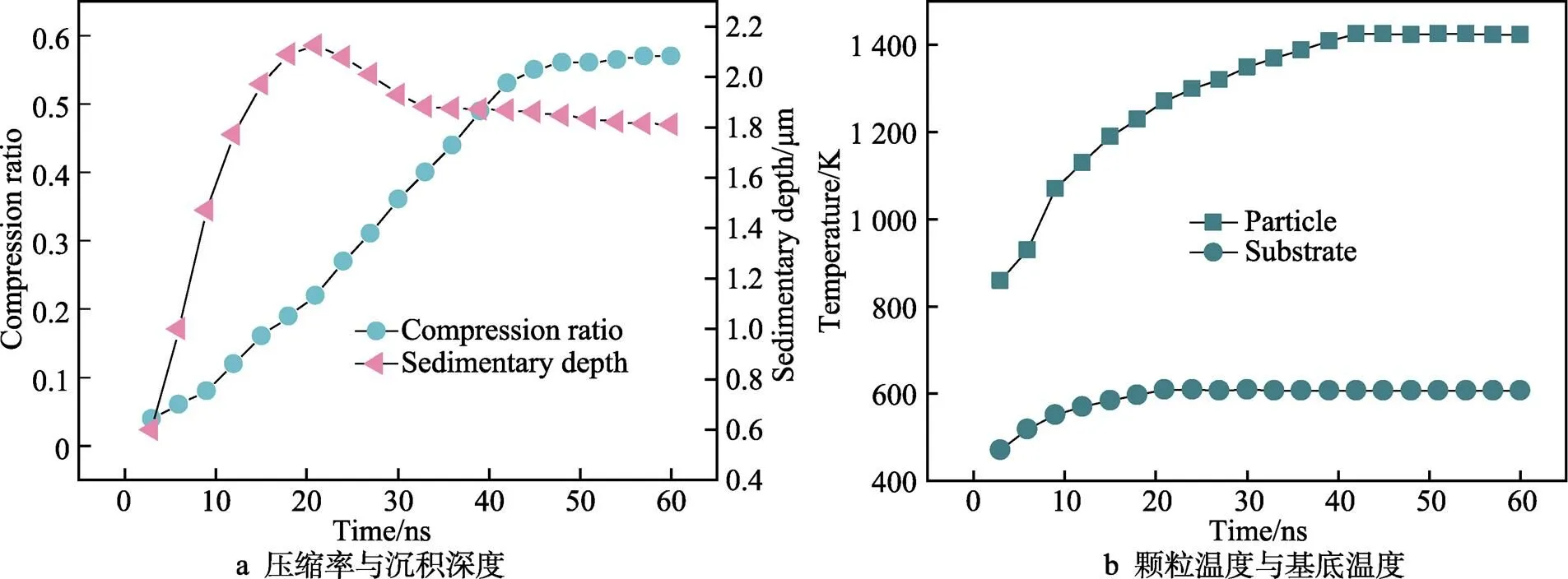
图8 颗粒冲击基底时压缩率、沉积深度及温度随时间的变化情况

2.2 入射角对颗粒沉积特性的影响

在超音速火焰实际喷涂时，由于基底表面具有一定的粗糙度，因此喷涂颗粒与基底碰撞时可能会呈一定倾斜角度，从而影响喷涂的沉积变形特性[26]。为了研究颗粒在不同入射角下的沉积特性，选取30 μm镍颗粒进行模拟，速度为450 m/s，初始温度为800 K，颗粒以不同入射角冲击基底（298 K）时的等效塑性应变云图如图9所示。由图9a可知，镍颗粒在入射角为15°时，颗粒与基体接触的表面迅速扩大，随着颗粒不断冲击左侧部分，与基体的间隙不断扩大，最终只有颗粒右侧部分黏结在基体上，这会减小颗粒与基底之间的实际接触面积。同时（如图9b～c所示），等效塑性应变最大值逐渐减小，从4.147 MPa减至3.144 MPa。这是因为入射角度增大，镍颗粒与基底冲击时的水平速度分量减小，即t减小。还可以看出，颗粒的右侧部分变形更加剧烈，颗粒与基底表面的有效接触面积不断扩大，颗粒的左侧部分也黏结在基底表面，这有助于颗粒与基底的结合，从而保证了涂层的质量。

随着入射角的改变，颗粒沉积基底上的深度有所区别。颗粒以不同入射角冲击基底，沉积得到的凹坑深度变化曲线如图10所示。由图10可知，随着入射角度的增大，颗粒在基底沉积的凹坑深度逐渐增大。这是因为入射角的增大，法向分速度也增大，即n增大。同时，入射角的增大导致颗粒与基底的结合强度增大，从而保证了涂层的质量。此外，在入射角为60°时，颗粒增大沉积深度的趋势最明显，结合图9的等效塑性应变云图可知，颗粒与基底接触集中区域呈现变形趋势，但冲击基底的凹坑不明显。这主要与颗粒速度、颗粒温度、基底温度，以及颗粒与基底的模量有着重要关系。

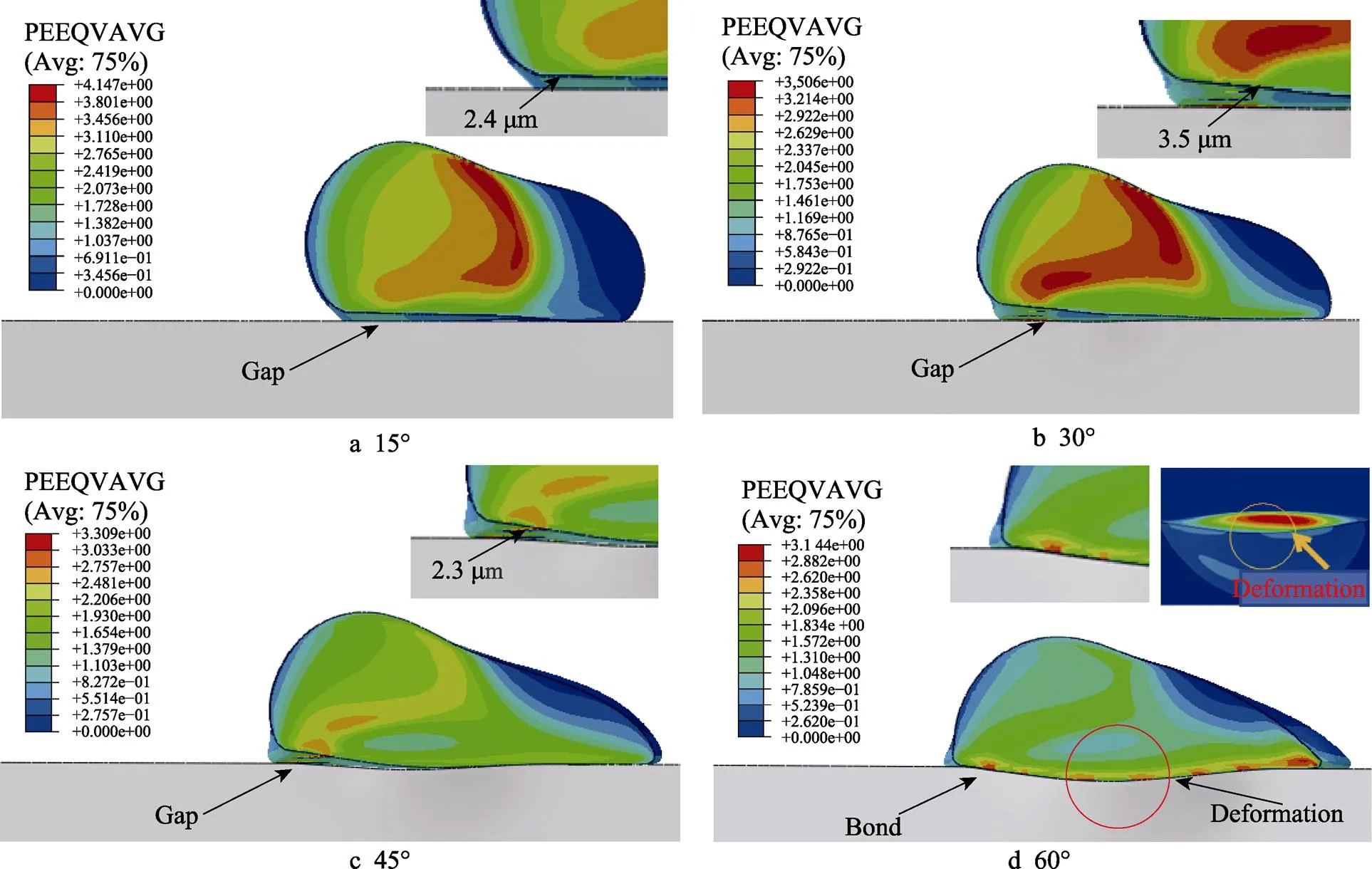
图9 不同入射角下颗粒的等效塑性云图

图10 不同入射角下的沉积深度

2.3 速度对颗粒沉积特性的影响

颗粒速度是影响热喷涂颗粒和基体结合效果的决定性因素之一[23]。为了研究颗粒速度对沉积特性的影响，选取30 μm的镍颗粒，设置初始条件：颗粒温度为800 K、基体温度为298 K。在不同速度下，颗粒在基体上沉积的等效塑性应变云图如图11所示。由图11可以看出，颗粒的等效塑性应变随着颗粒速度的增加而增大，从350 m/s时的2.876 MPa增至500 m/s时的4.351 MPa，应变效果提升的幅度较大。颗粒的变形程度逐渐增大，同时变形铺展范围也更宽泛，但颗粒冲击基体时形成的凹坑深度不明显。以350 m/s为例，此时颗粒冲击基体基本未形成凹坑，这会影响颗粒与基体的结合强度。值得注意的是（如图11c所示），在颗粒速度达到500 m/s时，颗粒的边缘材料向上翘曲，而不是像其他颗粒一样紧贴于基体，且向两边铺展。说明此时颗粒变形剧烈，发生了严重的金属射流，可能出现绝热剪切失稳现象[27]，使得颗粒与基体有效结合，有利于颗粒与基体的牢固结合，保证了涂层的结合强度。

为了验证上述模拟速度对颗粒变形的效果，HVOF颗粒速度由煤油与氧气提供，这里选取了3种不同工艺参数，如表3所示。利用3种不同工艺参数制备涂层，颗粒冲击基底的SEM形貌如图12所示。当采用工艺参数3时，由于氧气和煤油的流量较小，颗粒在燃烧室内获得的速度较小，使得颗粒冲击在基底上，下端未发生明显的金属射流现象，如图12a所示。当采用工艺参数2时，由于氧气和煤油的流量增大，颗粒获得速度增大（如图12b所示），可以发现颗粒下端部分出现金属射流现象。当采用工艺参数1时，获得速度再次增大（如图12c所示），可以清晰地观察到颗粒明显出现金属射流现象。由于速度过大，颗粒材料发生了裂开现象。说明颗粒速度越大，变形越明显，且金属射流现象更严重，发生了绝热剪切失稳现象，保证了颗粒与颗粒、基底的有效结合。

为了进一步说明颗粒速度对沉积特性的影响，模拟了颗粒速度对不同因素的影响，如图13所示。由图13a～b可知，颗粒压缩率和沉积坑深度均逐渐增加。随着颗粒初始速度的增加，依据动能定理，初始动能越大，则颗粒沉积在基底表面时的动能转化为更多的应变能，所以颗粒的变形程度更大。同时，这将对基体造成更大的冲击，从而增大基底塑性变形的程度，应变能转化为热能，提升了基底温度，促进了基底的软化，进一步增大了沉积坑深度。由此可见，提升颗粒的初始速度、增大基底软度将加深沉积坑的深度，促进颗粒的压缩变形，增大颗粒与基体的结合面积。同时，还弥补了沉积不规则造成的孔隙，提高了涂层的致密度[27]，使得涂层均匀平坦，从而获得了理想的涂层。

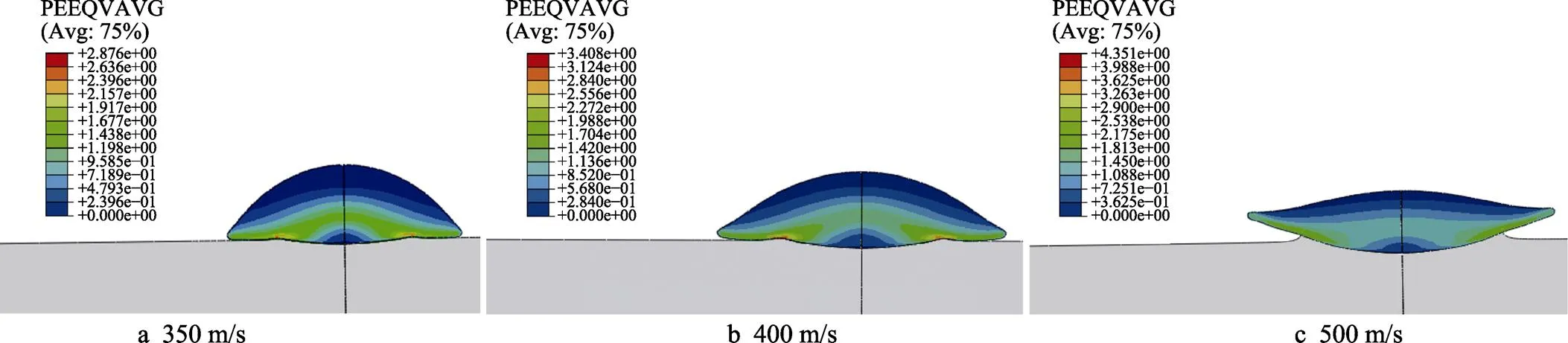
图11 不同速度下的等效塑性应变形云图

表3 不同工艺参数

Tab.3 Different process parameters

图12 不同速度下4 000倍SEM图

图13 颗粒速度对不同因素的影响曲线

为了验证结论，即颗粒速度越大，颗粒越扁平，形成的涂层越致密，孔隙率越低，这里同样采用3种不同工艺参数制备涂层（表3），以考察颗粒速度对涂层形貌、孔隙及厚度的影响。由图14a～b可以看出，在颗粒速度较小时，制备的涂层表面形貌呈现凹凸不平状态，存在许多无变形颗粒。如图14c所示，当速度进一步增至500 m/s时，获得的涂层更均匀平坦，且未见未变形小颗粒。这主要归因于颗粒的速度越大，变形越充分。如图14d～f所示，随着速度的增大，涂层越均匀，孔隙率越低。在颗粒速度较小时，涂层的孔隙和凹凸坑较多，这与前文的模拟结论一致。由图14g～i可以看出，颗粒的速度越大，涂层的厚度越厚，在速度较小时制备的涂层的厚度越薄。这主要是因为速度小的颗粒未牢固地沉积在基底上，导致部分颗粒发生了回弹[28]。

2.4 多颗粒重叠冲击基底的特性

目前，一些研究者认为后续颗粒的影响在涂层的沉积和结合中起着重要作用[29-30]。在传统的金属基底热喷涂沉积中，一般需要预热基底，这是为了减少热膨胀带来的应力问题。同时，当颗粒的冲击速度超过临界速度时，基底表面会形成致密的涂层。第1层金属颗粒与金属基底发生了较大的塑性变形，较软的材料因绝热剪切失稳产生了类似金属射流[31]。然而，对于沉积在金属基底表面的金属颗粒，由于塑性变形产生的热量使得冲击接触局部区域出现热软化，进一步降低了颗粒的模量，因此随后冲击的颗粒同时影响了先前的颗粒和基底。

为了研究多个颗粒重叠冲击基底的沉积特性，模拟了颗粒数量为1～4时的冲击基底特性，如图15所示。在初始速度为450 m/s、颗粒温度为1 100 K时，将30 μm的颗粒沉积在基底（450 K）上的等效塑性云图如图15所示，在颗粒的连续冲击下，颗粒与基底的接触面积逐渐增大，这对于提高颗粒在基底上的附着力有着积极作用。同时，处于涂层底部的颗粒受到后续颗粒的连续冲击下，压缩效果更加明显；颗粒间的空隙也会因后续颗粒的冲击变得更加夯实，涂层更加致密；处于涂层中间的颗粒也会在后续颗粒的冲击下再次变形，但变形程度小于底部颗粒，因此涂层相对稀疏；在涂层表面的颗粒因被冲击的次数较少，所以变形最弱，存在空隙区域未被夯实的现象，所以涂层最稀疏。另外，等效塑性应变逐渐增大，但第4个颗粒冲击完成时等效塑性应变略微下降，说明前3个颗粒回弹动能略大于第4个颗粒冲击动能。冲击时的等效塑性应变数值曲线与沉积深度柱状图如图16所示。

图14 不同工艺参数制备的涂层

由图16a可知，单个颗粒时的最大等效塑性应变为3.619 MPa，4个颗粒时的最大等效塑性应变为4.069 MPa。随着连续受冲击颗粒数量的增加，后一个颗粒对第1个颗粒的影响逐渐减小，其中在沉积过程中第1个颗粒的塑性变形最小。在2个颗粒的冲击下，基底和颗粒的塑性变形均增大。另外还可看出，当连续4个颗粒冲击发生时，颗粒的最大等效塑性应变出现减缓趋势，然而基底的最大等效塑性应变在第2个颗粒冲击时趋于稳定。这是因为第4个颗粒冲击动能的增加转化为4个颗粒的塑性变形变小。由图16b可知，在颗粒的连续冲击下，沉积深度不断增加，其中第2个颗粒的沉积深度增加的趋势最大，随后逐渐变缓，说明后续的颗粒冲击对第1个颗粒的作用越来越小。

在多颗粒重叠冲击时，基底表面温度分布轮廓云图如图17所示。如图17a所示，从基底来看，最高温度区主要出现在颗粒接触区域。在单个颗粒的情况下，最高温度为576.9 K，最高温度区的宽度约为18.1 μm。如图17b所示，在2个颗粒冲击情况下，颗粒的最高温度为876.4 K，该区域的宽度约为21.7 μm。在随后的颗粒冲击后，最高温度分别达到866.4、855 K，这与第2种情况无太大差异。可以得出结论，后续颗粒冲击对基底温度基本无影响。

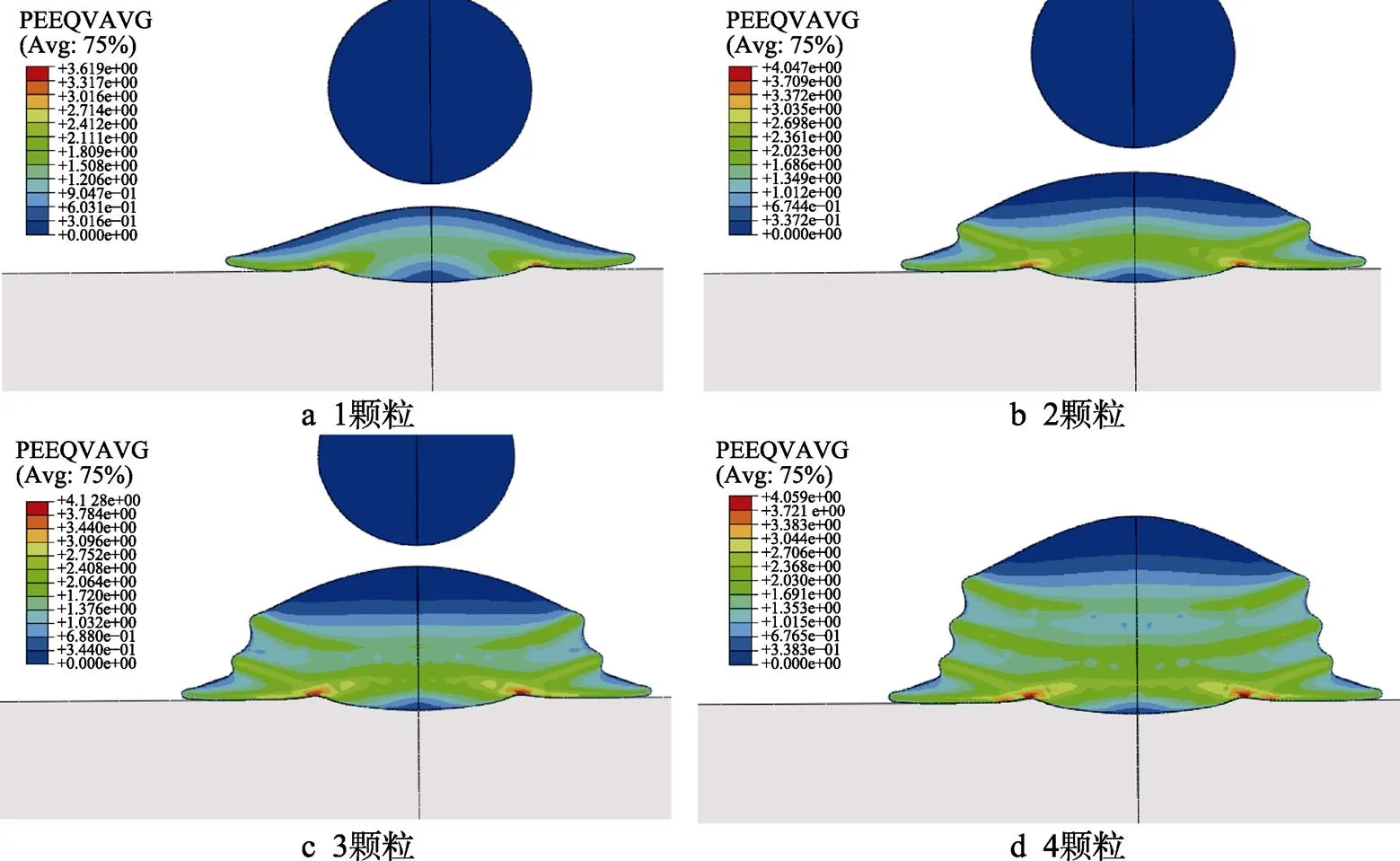
图15 多颗粒重叠冲击基底等效塑性云图

图16 4颗粒连续冲击时塑性应变与沉积深度

图17 基底温度的变化

在4个颗粒连续冲击基底表面时，第2个颗粒的等效塑性应变变化最明显，且对基底的影响最显著。第2个颗粒的冲击可以增大金属颗粒的塑性变形，从而使颗粒局部热软化。这会降低颗粒材料的应变硬化，从而增大颗粒的塑性变形能力，增大第1个颗粒的压缩效果，促进颗粒与颗粒之间的后续黏结。

2.5 多颗粒随机沉积特性分析

目前，针对热喷涂数值模拟的研究主要集中在单颗粒沉积数值模拟方面，对于多颗粒随机冲击的研究主要为有规律排列的相同粒径颗粒冲击模型。研究单颗粒沉积数值对于冷喷涂工艺具有一定的指导意义，但是实际喷涂情况较复杂。在制备涂层时，金属粉末被加速后撞击在基底上，在第1层颗粒撞击基底后，下一层颗粒的撞击不仅会与基底而且会与嵌入其中的颗粒相互作用。对于热喷涂，涂层的形成主要依靠颗粒的塑性变形和残余应力相互机械互锁，所以研究后续颗粒的随机冲击对于涂层的沉积机理有着重要的意义[15]。

在实际喷涂过程中，由于颗粒的尺寸、位置都是随机的，所以多颗粒沉积特性的数值模拟可以借助SolidWorks，并根据颗粒的粒径分布指定颗粒的位置，以随机生成多颗粒模型。不同粒径颗粒的速度和温度如图3c所示[17]。基底界面处的涂层颗粒如图18所示。由图18a可知，在400 ns时，在沉积过程中距离基底较近的颗粒已经发生严重变形，颗粒下端部分嵌入基底内部，可能会形成机械连锁，从而提升涂层的结合强度。金属材料还会向四周形成射流，等效塑性应变为3.964 MPa。在过高速度的冲击下，会使颗粒与基底产生侵蚀作用，这不利于在较薄的基底上制备涂层。在颗粒的不断冲击下，进行到800 ns时（如图18b所示），颗粒形成的金属射流已经发生了材料断裂现象。此时，在涂层内相邻颗粒之间观察到高塑性应变，表明涂层颗粒黏结，进一步保证了涂层的结合强度。这是因颗粒的温度过高，以及在高速度下与基底发生了碰撞。然而，金属颗粒材料溅射部分与基底的接触面积第2次增加，但溅射部分并未与基底发生冲击，无法形成范德华力，所以溅射部分材料不能增加颗粒与基底的结合强度[32]。在1 200 ns时（图18c），基于累积效应，最先冲击的金属颗粒与基底接触界面部分进一步软化，而基底部分出现过度变形和热膨胀，可能会被挤压到涂层颗粒之间的间隙中。同时，多颗粒的随机冲击使得间隙变小。在1 600 ns时（图18d），在过高速度的冲击下，颗粒完全从圆球形压缩成液滴状，从而形成涂层。金属材料溅射断裂现象越严重，则颗粒与颗粒之间的间隙越小。在后续喷射颗粒的冲击和沉积下，填充颗粒的形状不规则，颗粒未很好地压缩变形，此时颗粒的等效塑性应变为9.756 MPa。

前面运用ABAQUS观察了涂层颗粒的变化情况。为了更清楚地了解涂层表面的真实情况，利用JP800型的HVOF工艺设备制备出Ni基涂层，可见涂层表面呈现不规则形貌，如团聚、凹坑和未熔融粉末颗粒等不理想沉积形貌。这里借助SEM观察了涂层在不同倍数下的表面形貌，如图19所示。如图19a所示，在SEM 500倍下可以清晰地看到涂层颗粒在变形后形成了许多孔隙，还有未熔融的颗粒，形成了凹凸不平的表面形貌。为了了解颗粒变形是否充分，在SEM 2 000倍下进行观察（图19b），可清晰地看到经过火焰后，涂层部分颗粒获得的速度较低，温度较低，冲击基底时变形得不充分。同时，也有部分较小颗粒获得的速度和温度较高，在冲击基底后形成液滴状，且颗粒之间互相黏结，如图19c所示。同时，涂层材料发生断裂及溅射现象，并附着于涂层表面，如图19d所示。

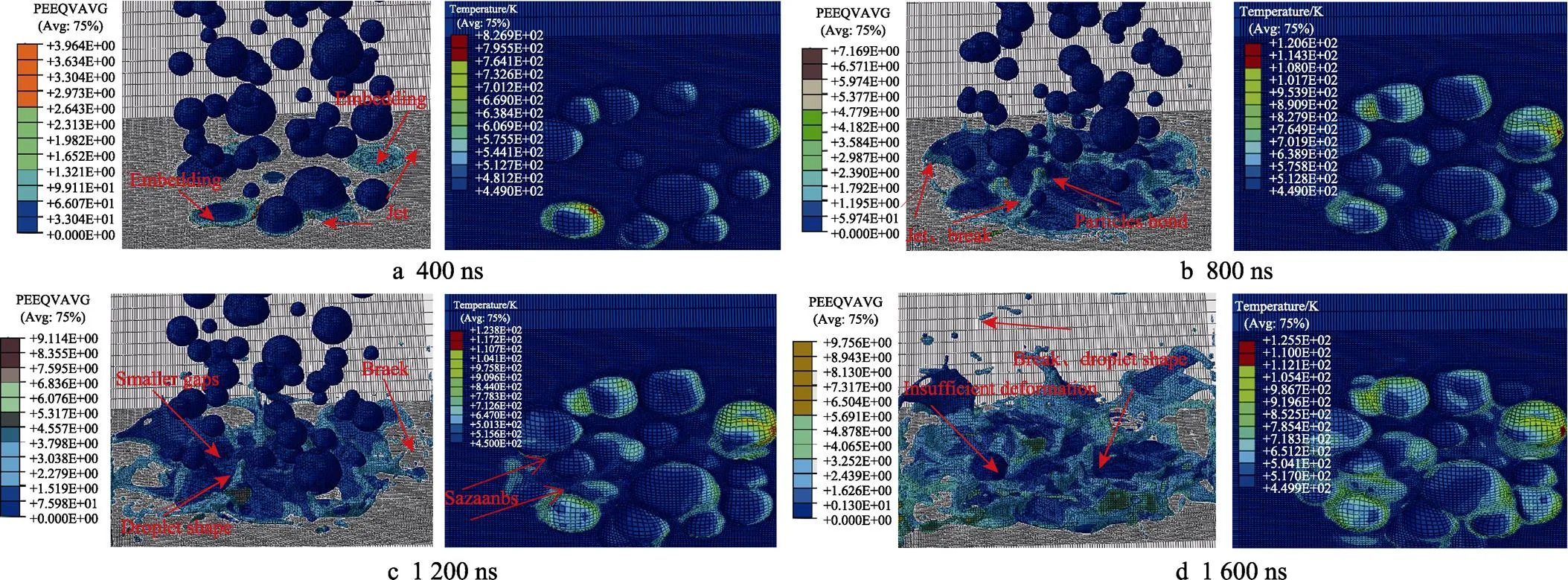
图18 多颗粒随机沉积等效塑性应变云图

图19 涂层颗粒表面SEM图

3 结论

采用数值模拟方法，系统研究了镍金属颗粒在HVOF过程中对304不锈钢基底的冲击行为，得出以下结论。

1）冲击模型网格越细，计算精确度越高，但是付出的时间成本越大。文中得出最合理的网格数量为1 752 912。通过实验验证了冲击模型，20 µm的颗粒冲击基底的能量较小，与基底的结合力较差；40 µm的颗粒冲击基底的能量较大，颗粒与基底的结合良好。

2）在颗粒入射角从15°增至45°时，颗粒与基底左侧出现间隙，这将减小颗粒与基底的结合强度。当颗粒入射角升至60°时，颗粒紧密黏结在基底上，对基底结合强度的增强效果明显。当颗粒速度从300 m/s升至500 m/s时会发生溅射现象，在这种情况下可能会发生绝热剪切失稳现象，使得颗粒与基底有效结合。此外，在颗粒速度为500 m/s时，所形成涂层的截面孔隙率最低。当4个颗粒冲击基底时，第2个颗粒在冲击完成时，颗粒和基底的等效塑性应变升至最大值，分别为4.047、1.47 MPa，沉积深度的变化趋势最大。同时，基底温度升至最大值（876.4 K）。在后续颗粒冲击完成时，其塑性应变与基底温度的变化很小。说明第2个颗粒对第1个颗粒及基底的冲击最明显，这有利于颗粒与颗粒之间的后续黏结。

3）当多颗粒随机冲击基底时，首先达到基底的颗粒发生了嵌入和溅射现象，表明镍颗粒与基底的结合为机械咬合。同时，在颗粒的不断冲击下，颗粒与颗粒之间发生了剧烈的塑性应变，且相互黏结。此外，通过实验和仿真对比可知，在后续颗粒的冲击和沉积下，填充颗粒的形状不规则，颗粒未得到较好的压缩变形，形成了一层孔隙较高且不平坦的金属涂层。

[1] 陈卫杰, 宋鹏, 高栋, 等. 航空发动机和工业燃气轮机热喷涂热障涂层用金属黏结层：回顾与展望[J]. 航空材料学报, 2022, 42(1): 15-24. CHEN Wei-jie, SONG Peng, GAO Dong, et al. Metallic Bond Coats for Thermally-Sprayed Thermal Barrier Coat­ings Applied to Aero-Engines and Industrial Gas Turbines: Review and Prospect[J]. Journal of Aeronautical Materials, 2022, 42(1): 15-24.

[2] SINGH J, KUMAR S, MOHAPATRA S K. Erosion Tribo-Performance of HVOF Deposited Stellite-6 and Colmonoy-88 Micron Layers on SS-316L[J]. Tribology International, 2020, 147: 105262.

[3] 姬寿长, 李争显, 陈丹, 等. 超音速火焰喷涂碳化钨技术及应用现状[J]. 榆林学院学报, 2021, 31(6): 1-10. JI Shou-chang, LI Zheng-xian, CHEN Dan, et al. Techno­logy and Application Status of Supersonic Flame Spray­ing Tungsten Carbide[J]. Journal of Yulin University, 2021, 31(6): 1-10.

[4] 王辉. 镍基粉末冶金高温合金钻削仿真与试验研究[D]. 济南: 济南大学, 2016. WANG Hui. Simulation and Experimental Study on Drilling of Nickel-Based Powder Metallurgy Superalloy [D]. Jinan: University of Jinan, 2016.

[5] 程国东, 万举惠. 铁基和镍基超声速火焰喷涂涂层滑动磨损行为研究[J]. 石油化工腐蚀与防护, 2020, 37(5): 6-9. CHENG Guo-dong, WAN Ju-hui. Study on Sliding Wear Behavior of Fe-Based and Ni-Based HVOF Sprayed Coatings[J]. Corrosion & Protection in Petrochemical Industry, 2020, 37(5): 6-9.

[6] ABBAS M, SMITH G M, MUNROE P R. Microstructural Investigation of Bonding and Melting- Induced Rebound of HVOF Sprayed Ni Particles on an Aluminum Substrate[J]. Surface and Coatings Technology, 2020, 402: 126353.

[7] 郝恩康. 超音速火焰喷涂NiCoCrAlYTa涂层的组织结构调控及性能研究[D]. 北京: 中国科学院大学, 2021. HAO En-kang. Study on Microstructure Control and Properties of NiCoCrAlYTa Coating Sprayed by Super­sonic Flame[D]. Beijing: University of Chinese Academy of Sciences, 2021.

[8] 苏威铭. 宽温域自润滑复合涂层NiCr-Cr3C2-BaF2·CaF2-Ag制备及性能研究[D]. 广州: 广东工业大学, 2020. SU Wei-ming. Preparation and Properties of Wide Temperature Range Self-Lubricating Composite Coating NiCr-Cr3C2-BaF2·CaF2-Ag[D]. Guangzhou: Guangdong University of Technology, 2020.

[9] 查柏林, 贾旭东, 王金金, 等. HVOF喷涂WC-12Co粒子沉积行为分析[J]. 表面技术, 2020, 49(11): 101-110. ZHA Bai-lin, JIA Xu-dong, WANG Jin-jin, et al. Analysis on Deposition Behaviour of WC-12Co Particles Sprayed by HVOF[J]. Surface Technology, 2020, 49(11): 101-110.

[10] ZANG Xue-rui, CAO Xue-wen, XIE Zhen-qiang, et al. Surface Deformation under Overlapping Impacts of Solid Particles[J]. Friction, 2023, 11(2): 280-301.

[11] KHAMSEPOUR P, MOREAU C, DOLATABADI A. Numerical Simulation of the Effect of Particle and Substrate Preheating on Porosity Level and Residual Stress of As-Sprayed Ti6Al4V Components[J]. Journal of Thermal Spray Technology, 2022, 31(1/2): 70-83.

[12] ASTARAEE A, COLOMBO C, BAGHERIFARD S. Numerical Modeling of Bond Formation in Polymer Surface Metallization Using Cold Spray[J]. Journal of Thermal Spray Technology, 2021, 30(7): 1765-1776.

[13] CHE Han-qing, VO P, YUE S. Investigation of Cold Spray on Polymers by Single Particle Impact Experiments [J]. Journal of Thermal Spray Technology, 2019, 28(1): 135-143.

[14] SONG Xu, NG K L, CHEA J M K, et al. Coupled Eulerian-Lagrangian (CEL) Simulation of Multiple Particle Impact during Metal Cold Spray Process for Coating Porosity Prediction[J]. Surface and Coatings Technology, 2020, 385: 125433.

[15] LIN En-qiang, CHEN Qi-yong, OZDEMIR O C, et al. Effects of Interface Bonding on the Residual Stresses in Cold-Sprayed Al-6061: A Numerical Investigation[J]. Journal of Thermal Spray Technology, 2019, 28(3): 472- 483.

[16] TANG Wei, ZHANG Jia-yuan, LI Yan, et al. Numerical Simulation of the Cold Spray Deposition of Copper Par­ticles on Polyether Ether Ketone (PEEK) Substrate[J]. Jour­nal of Thermal Spray Technology, 2021, 30(7): 1792-1809.

[17] 武云文, 刘思思, 谢玉莹, 等. 超音速火焰喷涂过程中粒子运动特性的数值模拟[J]. 材料科学与工艺, 2021, 29(5): 1-8. WU Yun-wen, LIU Si-si, XIE Yu-ying, et al. Numerical Simulation for Dynamic Characteristics of Particles during High-Velocity Oxygen-Fuel Spraying[J]. Materials Science and Technology, 2021, 29(5): 1-8.

[18] MENG Fan-chao, HU Dian-yin, GAO Ye, et al. Cold-Spray Bonding Mechanisms and Deposition Efficie­ncy Prediction for Particle/Substrate with Distinct Defor­mability[J]. Materials & Design, 2016, 109: 503-510.

[19] YIN Shuo, WANG Xiao-fang, SUO Xin-kun, et al. Depo­sition Behavior of Thermally Softened Copper Particles in Cold Spraying[J]. Acta Materialia, 2013, 61(14): 5105- 5118.

[20] 殷硕. 冷喷涂粉末粒子加速行为及沉积机理的研究[D]. 大连: 大连理工大学, 2012: 90. YIN Shuo. Study on Acceleration Behavior and Deposi­tion Mechanism of Cold Spraying Powder Particles[D]. Dalian: Dalian University of Technology, 2012: 90.

[21] 陆冠雄, 孙策, 郝利军, 等. 超音速火焰喷涂焰流特性和粒子沉积行为[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(3): 275-283. LU Guan-xiong, SUN Ce, HAO Li-jun, et al. Gas Flow Characteristics and Particle Impact Behavior in High Velocity Oxygen/Air Fuel Process[J]. Journal of Tianjin University (Science and Technology), 2015, 48(3): 275- 283.

[22] 叶福兴, 牛安宁, 郭磊, 等. HVOF喷涂WC-17Co粉末的粒子撞击行为研究[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(8): 882-887. YE Fu-xing, NIU An-ning, GUO Lei, et al. Impact Beha­vior of WC-17Co Particle in HVOF Spraying[J]. Journal of Tianjin University (Science and Technology), 2016, 49(8): 882-887.

[23] YU M, LI W Y, WANG F F, et al. Effect of Particle and Substrate Preheating on Particle Deformation Behavior in Cold Spraying[J]. Surface and Coatings Technology, 2013, 220: 174-178.

[24] REN Bai-hua, SONG Jun. Peridynamic Simulation of Particles Impact and Interfacial Bonding in Cold Spray Process[J]. Journal of Thermal Spray Technology, 2022, 31(6): 1827-1843.

[25] FARDAN A, BERNDT C, AHMED R. Numerical Model­ling of Particle Impact and Residual Stresses in Cold Sprayed Coatings: A Review[J]. Journal of Thermal Spray Technololgy, 2021, 409: 0257-8972.

[26] NOURIAN A, SCHWARTZ T, BOESE S, et al. Effects of Process Parameters on Cold Spray Deposition of Al-6061 Alloy[J]. Journal of Thermal Spray Technology, 2022, 31(8): 2517-2536.

[27] 孙策. HVOF喷涂粒子与基体碰撞沉积行为研究[D]. 天津: 天津大学, 2014: 20-21. SUN Ce. Study on Collision and Deposition Behavior of HVOF Spraying Particles with Substrate[D]. Tianjin: Tianjin University, 2014: 20-21.

[28] 史周琨, 徐丽萍, 张吉阜, 等. HVOF制备铝青铜涂层工艺优化及工艺参数对涂层性能的影响[J]. 表面技术, 2021, 50(8): 101-108. SHI Zhou-kun, XU Li-ping, ZHANG Ji-fu, et al. Opti­mization of Preparation Process of Aluminum Bronze Coating by HVOF and Effect of Process Parameters on Coating Properties[J]. Surface Technology, 2021, 50(8): 101-108.

[29] XIE Ying-chun, YIN Shuo, CHEN Chao-yue, et al. New Insights into the Coating/Substrate Interfacial Bonding Mechanism in Cold Spray[J]. Scripta Materialia, 2016, 125: 1-4.

[30] ZHOU Hong-xia, LI Cheng-xin, BENNETT C, et al. Numerical Analysis of Deformation Behavior and Inter­face Bonding of Ti6Al4V Particle after Subsequent Impact during Cold Spraying[J]. Journal of Thermal Spray Tech­nology, 2021, 30(4): 1093-1106.

[31] BAE G, XIONG Yu-ming, KUMAR S, et al. General Aspects of Interface Bonding in Kinetic Sprayed Coatings [J]. Acta Materialia, 2008, 56(17): 4858-4868.

[32] 牛安宁. 超音速火焰喷涂中粒子与基体撞击行为的数值研究[D]. 天津: 天津大学, 2015: 56. NIU An-ning. Numerical Study on the Impact Behavior between Particles and Substrate in Supersonic Flame Spraying[D]. Tianjin: Tianjin University, 2015: 56.

Numerical Simulation of Particle Deposition Behavior of Ni-based Coatings by High-velocity Oxy-fuel Spraying

,*,,,

(School of Mechanical Engineering and Mechanics, Xiangtan University, Hunan Xiangtan 411105, China)

In order to explore the deposition characteristics of thermal spraying coating particles, it is necessary to consider the effect of subsequent random impact of particles with different particle sizes. In the research related to deposition characteristics of coating particles, many researchers mainly focus on the particles with the same particle size to impact together in neat rows. However in the actual spraying, the powder particles are interval powders, with particles with different particle sizes, and the impact on the substrate is also random. Therefore, few people consider this problem. In this work, a particle and substrate impact model was established in ABAQUS to study grid convergence based on dent depth and stress distribution of particle impact. At the same time, the reliability of the model was verified by experiments. Then, the deposition characteristics of the substrate impacted by particles at different incident angles, and the deposition characteristics when four particles continuously overlapped and impacted the substrate and multiple particles randomly impacted the substrate surface were analyzed with the validation model.The optimal grid number of the sediment model was 1 752 912, which not only reduced the calculation cost, but also obtained accurate results. The particle with a particle size of 20 µm had a large impact speed, but a large resilience, and poor adhesion to the substrate. The particle with a particle size of 40 µm had a moderate speed, but a large impact energy, so it had a good interface with the substrate. The incident angle of particles increased from 15° to 60°, and the particles were better attached to the substrate surface, when the particle velocity increased from 350 m/s to 500 m/s, sputtering may occur, which may cause adiabatic shear instability and form effective bonding. When four particles impacted the substrate, the deformation of the second particle and its effect on the substrate were the most obvious. When multiple particles with different particle sizes impacted the substrate at random, the shape of the filling particles was irregular due to the impact and deposition of subsequent particles, and the first layer of particles may form a mechanical bite with the substrate. Thermal spraying should be inclined at a certain angle and increased at a certain speed, which can expand the contact area between particles and substrate. At the same time, the deposition depth increases continuously to enhance the adhesion, so it is more conducive to the preparation of the coating. When the particles overlap and impact, the subsequent particles make the first particle increase the compression effect and embed more deeply into the stainless steel substrate, which is conducive to the subsequent bonding between particles and makes the coating more compact. When a number of particles with different particle sizes impact the substrate at random, due to the different initial velocities and temperatures obtained by the subsequent particles in the thermal spraying gun tube, the particles impact and deposit in the later stage, and there is no good flatness or deformation. At the same time, high plastic strain is observed between the first layer of deposited particles and the substrate, as well as between adjacent particles in the coating. This situation indicates that the coating is bonded, so it is necessary to increase the full combustion of oxygen and kerosene to fully soften particles with different particle sizes during the actual thermal spraying. At the same time, the best efforts should be made to obtain higher speed under the gun barrel air pressure. When impacting the substrate, it can be completely deformed, so as to obtain an ideal high-quality coating.

high-velocity oxy-fuel spraying; mechanical occlusion; multi particles; overlapping impact; ABAQUS simulation.

2022-10-26；

2023-03-02

TG174.44

A

1001-3660(2023)10-0321-14

10.16490/j.cnki.issn.1001-3660.2023.10.028

2022-10-26；

2023-03-02

国家自然科学基金面上项目（52175191）；湖南省“荷尖”创新人才工程项目（2022RC1033）

National Natural Science Foundation of China (52175191); Hunan Province "Lotus Tip" Innovative Talent Project (2022RC1033)

许耀飞, 刘思思, 杨正航, 等.超音速火焰喷涂镍基涂层颗粒沉积特性的数值模拟[J]. 表面技术, 2023, 52(10): 321-334.

XU Yao-fei, LIU Si-si, YANG Zheng-hang, et al. Numerical Simulation of Particle Deposition Behavior of Ni-based Coatings by High-velocity Oxy-fuel Spraying[J]. Surface Technology, 2023, 52(10): 321-334.

通信作者（Corresponding author）

责任编辑：彭颋