Analysis and Optimization of Validation Procedure in Blockchain-Enhanced Wireless Resource Sharing and Transactions

Enyu Du,Yang Gao,Wenjun Wu,Zhaoxin Yang,Yufeng Yin,Pengbo Si

Faculty of Information Technology,Beijing University of Technology,Beijing 100124,China

*The corresponding author,email: wenjunwu@bjut.edu.cn

Abstract: To ensure the security of resource and intelligence sharing in 6G,blockchain has been widely adopted in wireless communications and applications.Although blockchain can ensure the traceability and non-tamperability of data in the concatenated blocks,it cannot guarantee the honest behaviors of users in the application before the generation of transactions.Thus,additional technologies are required to ensure that the source of blockchain data is reliable.In this paper,the detailed procedure is designed for the application-oriented task validation in the blockchainenhanced computing resource sharing and transactions in ultra dense networks (UDN).The corresponding queuing model is built and analyzed with the consideration of the wireless re-transmission and the probability of malicious deception by users.Based on the analysis results,the UDN deployment is optimized to save network cost while ensuring latency performance.Numerical results verify our analysis,and the optimized system deployment including the number and service capacities of both base stations and mobile edge computing(MEC)servers are also given with various system settings.

Keywords: blockchain;queuing theory;wireless resource sharing;validation procedure

I.INTRODUCTION

As 6G is transforming wireless communication from“connected things”to“connected intelligence”,security has become more and more important [1].With the advantages of data traceability and irreversibility,blockchain has been recognized as a promising paradigm to address the security issue.It is also capable to build the willingness incentive and billing system for resource and information sharing in the future network[2].

Integrating blockchain with wireless communications and applications has aroused considerable attention in recent research.In the edge caching system,blockchain combining with physical layer security technologies is adopted to prevent data from being tampered with and eavesdropped [3].For the dynamic resource sharing in 6G,blockchain is used to improve the distribution,security and automation[4].In the internet of things (IoT),blockchain has also been applied to ensure data security and privacy [5].Moreover,a public management platform to register and manage the information of IoT devices is built by integrating blockchain with a hybrid cloud [6].A new routing and a private communication blockchain framework is designed for wireless sensor network to reduce the power,computation,and memory consumption[7].Blockchain is also used to maintain the synchronization of the sensor data of the entire wireless network through the concatenated blocks[8].To solve the data security problems in artificial intelligence(AI)applications,the blockchain-enhanced decentralized and secure data sharing technique without a so-called trusted third entity is proposed in [9].A blockchain and AI-empowered telesurgery system towards 6G is also proposed,in which blockchain is used to manage the surgeons’ authority and verify their credentials before the initiation of surgical procedure[10].

Although blockchain can ensure the traceability and non-tamperability of data in the concatenated blocks,it cannot guarantee the honesty of the application user since the records of the applications other than the original application data join in the blockchain.Taking the computing resource sharing as an example,the requester may deliberately mark the correct results as errors to evade the payments,and the resource provider may also directly return a wrong result to defraud the service fee without calculation.Therefore,to support wireless communications and applications,the application task validation procedure should be considered according to the specific application scenarios,which is different from the traditional validation process for monetary transactions.

In the existing studies,the validation scheme for blockchain is mainly divided into two methods.One is a built-in validation scheme in the traditional blockchain system.Generally,at the end of the application service process and before the generation of the transaction,the system will validate the correctness of the transaction according to relevant laws and contracts stipulated in advance[11–13].Moreover,before the transaction is uploaded to the chain,the miner will validate the transaction through the fixed information obtained from the smart contract [14,15].However,the flexibility of this traditional verification method is limited,and the content is relatively simple and fixed.Therefore,the researchers proposed the second validation scheme to meet the requirements of the complex and specific applications by adding the validator.In the V2V scenario,nearby vehicles will be randomly selected as the validators to validate the data when the doubtful data appears in the system[16].Due to that the randomly selected vehicles are not absolutely reliable,the high-level authority is required to make the final judgment when the data is still in doubt after the validation,which will lead to the decline of timeliness.Therefore,how to effectively validate the data while simultaneously guaranteeing high reliability and low latency is the key point.

In blockchain-enhanced wireless networks with distributed computing resources,a task validation procedure is designed in the smart contract to guarantee the honest behaviours of the computing resource requester and provider [2].However,the detailed analysis and optimization for the procedure need further researched.

In this paper,the blockchain-enhanced computing resource sharing and transactions in UDN is proposed inspiring by the architecture of B-ReST[2].Considering the characteristics of wireless transmissions,the application-oriented task validation procedure is designed,and the corresponding queuing model is built and analyzed.Based on the analysis results,the UDN deployment is optimized to save network cost while ensuring latency performance.Numerical results verify our analysis,and simulation results of system deployment optimization are also given.The contributions of this paper are concluded as follows.

1) The system architecture and workflow which realize the application-oriented task validation process of the blockchain-based computing resource sharing in UDN is designed.The transactions that record the resource sharing and validation process are defined.Moreover,the necessary information that required in the validation is contained in the transactions and stored in the blockchain to ensure fairness.

2) The resource sharing and validation process is analyzed based on queuing theory.The whole process is modeled as a two-stage queuing system,which represents the resource sharing process and validation process,respectively.Each stage contains several parallel service branches,each of which consists of a wireless transmission queuing system and a MEC queuing system of a certain base station (BS).The latency of the whole process is calculated with the consideration of wireless re-transmission and the probability of malicious deception of users.

3) The UDN deployment including the number and service capacities of both BSs and MEC servers is optimized.The cost of BSs and the MEC servers as well as the latency of the whole resource sharing process are considered as the system cost.The classic convex optimization theory is applied to solve the problem of minimizing the cost.The optimized UDN deployment parameters are obtained through calculation,and numerical results also confirm the analytical results.

The rest of this paper is organized as follows.Section II presents the physical architecture design.The queuing model adopted in the proposed scheme is described in Section III.Then the deployment optimization is designed in Section IV.In Section V,the simulation and optimization results are shown to be analyzed.Finally,in Section VI,the conclusion and the future works are given.

II.SYSTEM MODEL

2.1 Scenario

Based on the blockchain-enabled resource sharing and transactions system proposed in [2],a specific UDN scenario with task validation function is considered in this paper.

As shown in Figure 1,there are two basic kinds of network elements,i.e.,user equipments(UEs)and small BSs,which are randomly scattered in the system.UEs generate tasks and requests for computing resources,and BSs with mobile edge computing(MEC)servers are computing resource providers.

Figure 1.The optimized physical architecture.

Since blockchain is used to build the willingness incentive and billing mechanism in the network[2],UEs and BSs also participate as blockchain nodes which are named as blockchain-enabled UEs (B-UEs) and blockchain-enabled BSs(B-BSs),respectively.

To implement the task validation function,B-BSs are classified into two subsets,the blockchain-enabled service nodes (B-SNs) and the blockchain-enabled validation nodes (B-VNs).To ensure the impartiality of the final judgment,the B-VNs are selected from the B-BSs through the reputation-based voting,and the BBS can become a B-VN only when it has completed a certain number of tasks and has a high reputation.

Denoted byU={uj}j=1,...,J,S={sk}k=1,...,KsandV={vk}k=1,...,Kvthe sets of B-UEs,B-SNs and B-VNs,respectively.Obviously,the set of B-BSsB={bk}k=1,...,Kb=S∪VandKb=Ks+Kv.

Without loss of generality,assume each B-UE generates tasks independently following the Poisson process.Therefore,the task generating process of the whole system is still a Poisson process.Define the task generating rate asλwtasks per hour,and different tasks have different data sizes and computing resource requirements.

Although the qualities of wireless channels between B-UEs and B-BSs vary a lot,the average transmission rate which each B-BS can provide can be calculated or simulated through spatial Poisson point process(SPPP)-based ergodic capacity analysis and simulation[17].When all the B-BSs in the UDN have the same configuration and equal bandwidth resources,their average transmission capability can be quantified asµwtasks per hour from the perspective of statistical analysis.To reflect the randomness of wireless channel quality and the difference in task data size,we assume the transmission duration of each task follows a negative exponential distribution withµwas the parameter.

The computing capability of each B-BS with an MEC server is quantified asµctasks per hour.Similarly,the computation duration of each task also follows a negative exponential distribution withµcas the parameter,which reflects the difference in task computing resource requirement.

2.2 Workflow

To avoid the dishonest behaviours of both B-UEs and B-SNs,the resource sharing and transactions process consists of two phases,i.e.,the service phase and the validation phase,as shown in Figure 2.

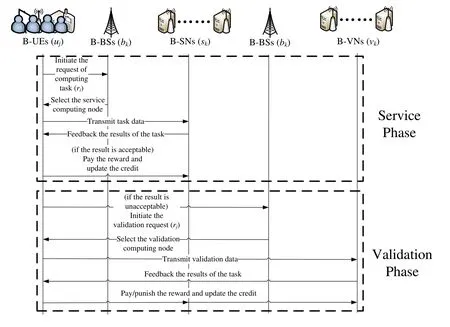
Figure 2.Workflow of resource sharing and transactions.

2.2.1 Service Phase

The service phase basically follows the workflow given in[2],and some specifci modifciations are made according to the UDN scenario.

•The B-UEujgenerates a taskriwhich requests for computing resources.A transactionRS_Requestithat records the data size,time limit and task validation rule and the payment of the task,the historical reputation of the B-UE as well as other necessary information for wireless channel quality testing is generated and sent to all B-SNs that cover this B-UE.RS_Requestiis also packaged into a block and joins the chain.

•The B-SNs decide whether to accept taskrior not after they received the transactionRS_Requesti.This is actually a requester and provider matching process which can be implemented using random,greedy and other intelligent algorithms[18].In the analysis in this work,the random requester and provider matching algorithm is adopted.Assume B-SNskaccepts this request andujdecides to use the resource shared fromsk.

•The B-UEujsends the original data ofritoskthrough wireless channel,and the re-transmission is enabled if the frist transmission failed.Then,skcalculatesrion its MEC server and gets the result.A transactionRS_Calculatedithat records the results,accomplish time and charge of the task,the historical reputation of the B-SN is generated and sent to the B-UE.RS_Calculatediis also packaged into a block and joins the chain.

•If the results are out of time,skmust payujthe system-defnied compensation fee.If B-UE confrims the results,the predefnied payment is reduced fromuj’s account,and accordingly,the payment is added tosk’s account.The reputations ofskandujare updated according to the task response,and a transactionRS_Confirmjthat records updated reputation and account balances of the B-UE and B-SN is generated and packaged into a block to join the chain.If B-UE rejects the results,the validation process is automatically ac

tivated at the B-UE.

2.2.2 Validation Phase

To judge the dishonest behaviours,the validation phase is designed.

•When the validation process is automatically activated at the B-UE,a transactionRS_ValidateRequestjthat records the index of the task is generated and sent to all the B-VNs that server this area.It is also packaged into a block and joins the chain.

•As the B-VNs are selected according to the historical reputation,anyone of them can accomplish the validation.Assume B-VNvmaccepts the validation request ofrjin a random manner.

•Then B-VNvmuses the index of taskrjin transactionRS_ValidateRequestjto look up the results,task validation rule and payment of taskrjfrom the blockchain,and calculate the fnial judgement.If the fnial judgment shows that the results are correct,ujmust payskthe system defnied compensation fee in addition to the predefnied payment of taskrj,andujmust payvmthe system defnied validation fee.If the fnial judgment shows that the results are wrong,skmust payujthe system defnied compensation fee,andskmust payvmthe system defnied validation fee.The reputations ofskandujare update according to the fnial judgement.The transactionRSConfirmjthat records updated reputation and account balances of the B-UE and BSN is generated,and a transactionRS_Validatejrecording fnial judgement of the task and the account balance of the B-VN is generated.Both the two transactions are packaged to join the chain.

III.QUEUING THEORY-BASED ANALYSIS OF RESOURCE SHARING LATENCY

Based on the workflow given in the previous section,the whole process is modeled as a two-stage queuing system as shown in Figure 3.

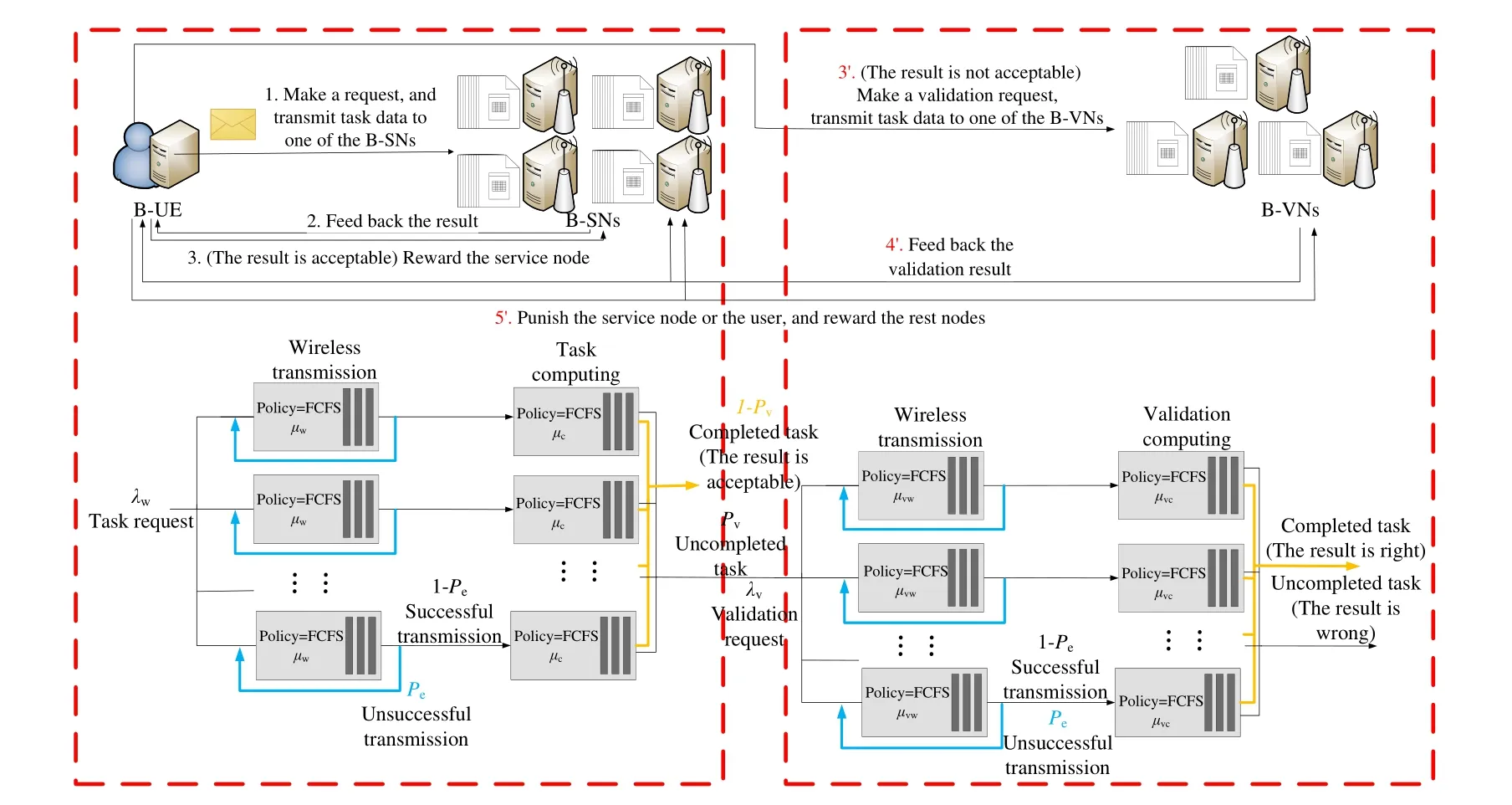
Figure 3.Two-stage queuing system.

3.1 Analysis of the Service Phase

The first stage which consists ofKsparallel service branches of all B-SNs represents the resource sharing process.Adopting the basic random UE access strategy,the Poisson flow of task arrival is randomly decomposed intoKcsub-processes each of which is the task arrival process of each B-SN.According to superposition theorem [19],all theKctask arrival processes are still Poisson processes,and their rates areλw,k=λw/Ks.

Each service branch is further modeled as the series connection of a wireless transmission queuing system and a MEC queuing system.In the following,the service branch of thek-th B-SN is analyzed as an example.

3.1.1 Analysis of the Wireless Transmission Queue

For the wireless transmission queuing system,the task arrival process is a Poisson process and the transmission duration of each task follows a negative exponential distribution withµwas parameter.Thus it can be modeled as a M/M/1 queuing model.Besides,the wireless transmission failures caused by radio interference or serious fading are also taken into account,and those failed task will trigger a re-transmission.Denoted byPethe probability of the unsuccessful transmission in the queuing model.

The state transition diagram of a wireless transmission queuing system is shown in Figure 4,where the statenis the number of tasks in the system,and it may be any non-negative integer number.The state transition equations can be formulated as

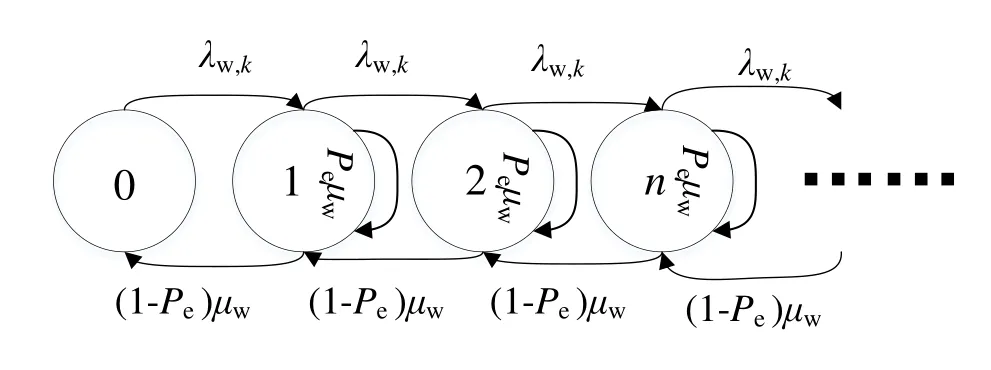
Figure 4.A scheme of “birth-death” process of wireless transmission.

wherepn,kis the stationary probability of statenin the wireless transmission queue of thek-th B-SN.Taking the special staten=0 into consideration,a set of algebraic equations for the stationary system state is given as

Then,the stationary probability of the staten≥1 can be derived as

We can obtain that

Based on the stationary probability of state,the average number of tasks in the systemLw,kand the average transmission latencyτw,kcan be obtained as

3.1.2 Analysis of the MEC Queue

When the wireless transmission of a task is accomplished,it will join the queue of the MEC server deployed at the B-SN immediately.According to Burke’s theorem [20],the output of an M/M/1 queue with arrival rateλis also a Poisson process of the same rate if the queue is in the steady state.Therefore,the output of the wireless transmission queue,which is also the arrival process of the MEC queue,is a Poisson process of rateλc,k=λw,k.Since the computation duration of each task also follows a negative exponential distribution withµcas a parameter,the MEC queue is a standard M/M/1 queue.Thus,the state transition equations are

whereqn,kdenotes the stationary probability of staten≥1 in the MEC queue of thek-th B-SN.

Then,the stationary probability of staten≥1 can be calculated as

Further,the average number of tasksLc,kand the average tasks processing latencyτc,kin the MEC queue system are derived as

Since all B-SNs have the same configuration and the tasks are random access to the B-SNs,the average latency of theKcparallel service branches of the first stage is the same.Hence,in the resource sharing service phase,the average task transmission latencyτwand average tasks processing latencyτcare given by

Obviously,the output of thek-th MEC queue is still a Poisson process of rateλc,kusing the Burke’s theorem[20]again.Since each B-SN serves the tasks independently,theseKsoutput Poisson processes are combined into a new Poisson process of rateλc,kKs=λw.This is to say the output of the first stage queuing system is still a Poisson process.

3.2 Analysis of the Validation Phase

The second stage which has a similar structure to the first stage represents the validation process.When the task computing is accomplished,UE may not accept the results.Assume this is a random behavior,and the probability of rejecting the results is denoted byPv.Therefore,the validation requests arrive as a Poisson process with rateλv=Pvλw.

Since the validation phase also consists of the wireless transmission and validation computing of each task,its queuing model is similar to the service phase.The average transmission latencyτvwand validation processing latencyτvcare given as

Connecting the two-stage together,the overall average latency of all tasks can be calculated as

IV.SYSTEM DEPLOYMENT OPTIMIZATION

To serve the tasks economically and efficiently,the system cost should be limited while ensuring the acceptable latency performance.Therefore,the cost of BSs providing wireless transmission capabilities and the MEC servers providing computing capabilities as well as the latency of the whole resource sharing process is considered as the system utility.Define

whereα1,α2andα3are the weights,andα1+α2+α3=1.RwandRcare the cost of deploying a unit of transmission resource and a unit of computing resource,respectively.Ruis the penalty of latency.

Taking the stability constraints of queuing systems into account,the system deployment optimization problem can be modeled as

Taking (12),(13),(14),(15) and (16) into (18),we find that the six variables can be divided into two independent groups(Ks,µw,µc)and(Kv,µvw,µvc).In the following,we first solve the optimization problem considering the first group of variables (Ks,µw,µc),and then,extended to another group of variables straightforwardly.

The convexity of the system utility function is confirmed first.The second derivative ofFwith respect to the variables(Ks,µw,µc)is

Since the convex functionFobtains the optimal value when the first derivative is equal to 0,the equations are given as

Each of the above equations can be solved as

where

and

Since the third equation of(20)is a quartic equation,it is difficult to obtain a closed-form optimal solution.Thus,the iterative solution method is used,and the solving process is given in Algorithm 1.

Extending the solution of (Ks,µw,µc) to(Kv,µvw,µvc),we obtain that

where

and

The iterative solving process given in Algorithm 1 is still applicable for finding the optimal solution of

V.NUMERICAL RESULTS

5.1 Verify the Theoretical Analysis

Simulations are conducted to verify the theoretical analysis.We first evaluated the accuracy of the average latency given by queuing theory-based analysis.Then,the system deployment optimization results are also confirmed.

The basic system parameters for verifying the analytical latency are given in Table 1.To test the analytical results comprehensively,we designed 8 experiments,each of which is conducted with one varying system parameter while keeping others set as the values given in Table 1.Simulation results are given in Figure 5,Figure 6 and Figure 7.All the results show that the analytical average latency matches the simulation results well.

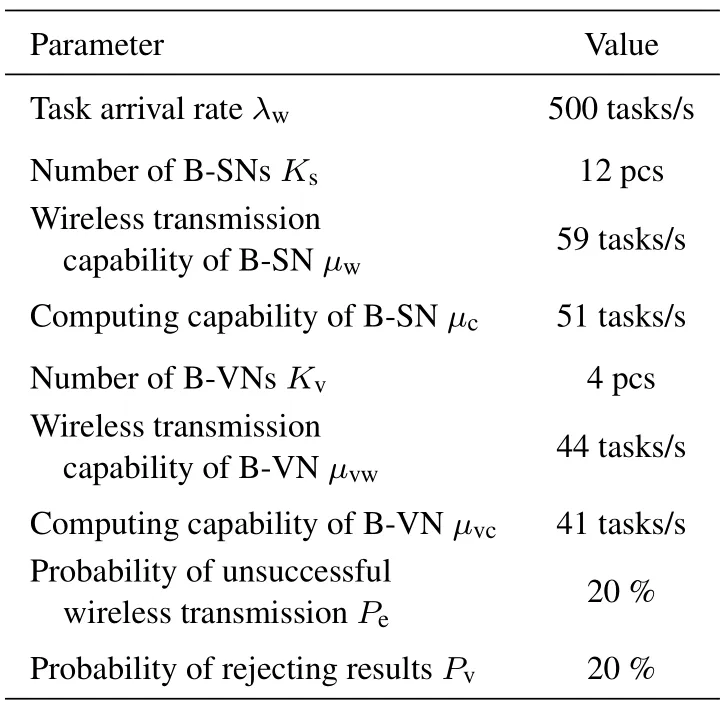
Table 1.System parameters for verifying the analytical latency.

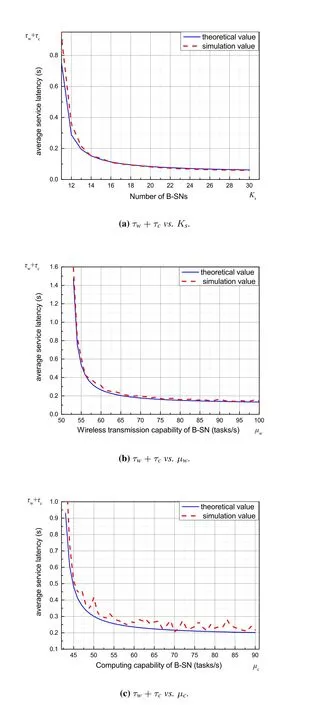
Figure 5.Average latency of service phase vs. varying system parameters.

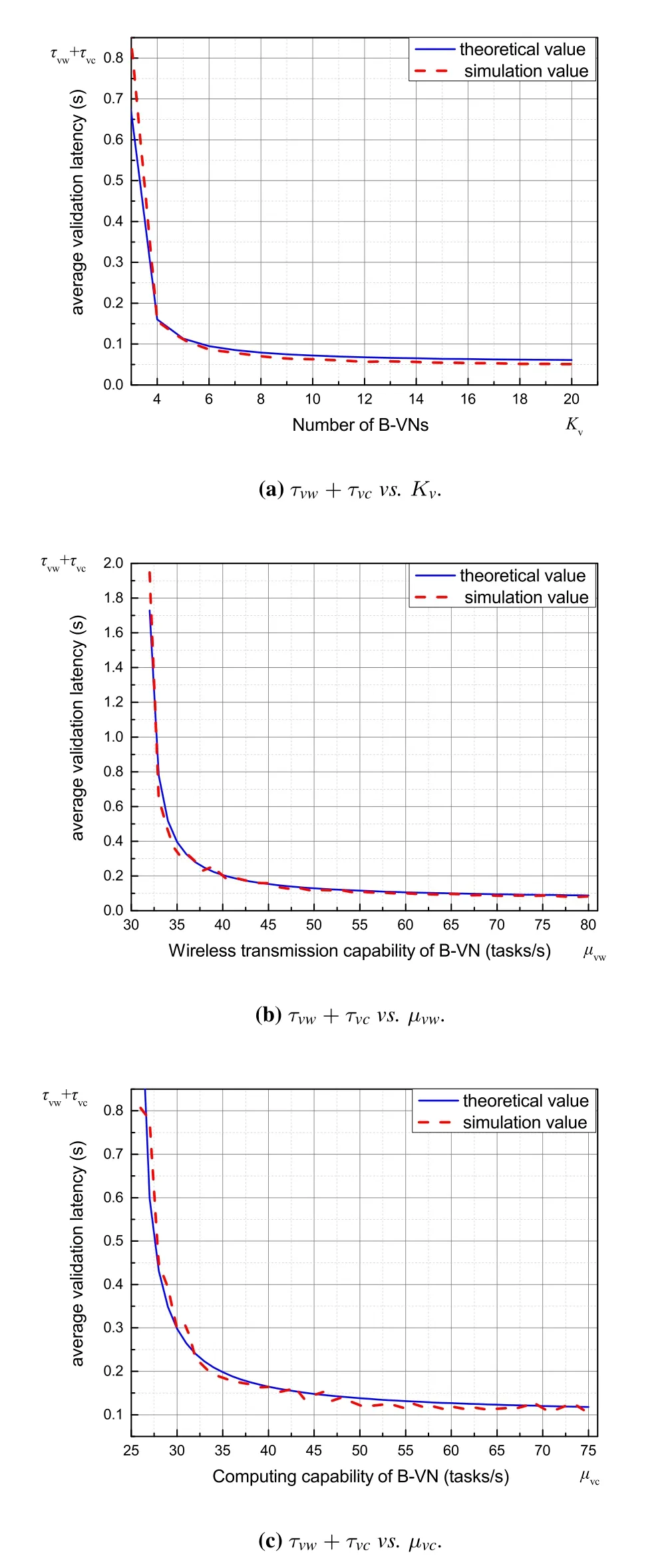
Figure 6.Average latency of validation phase vs. varying system parameters.

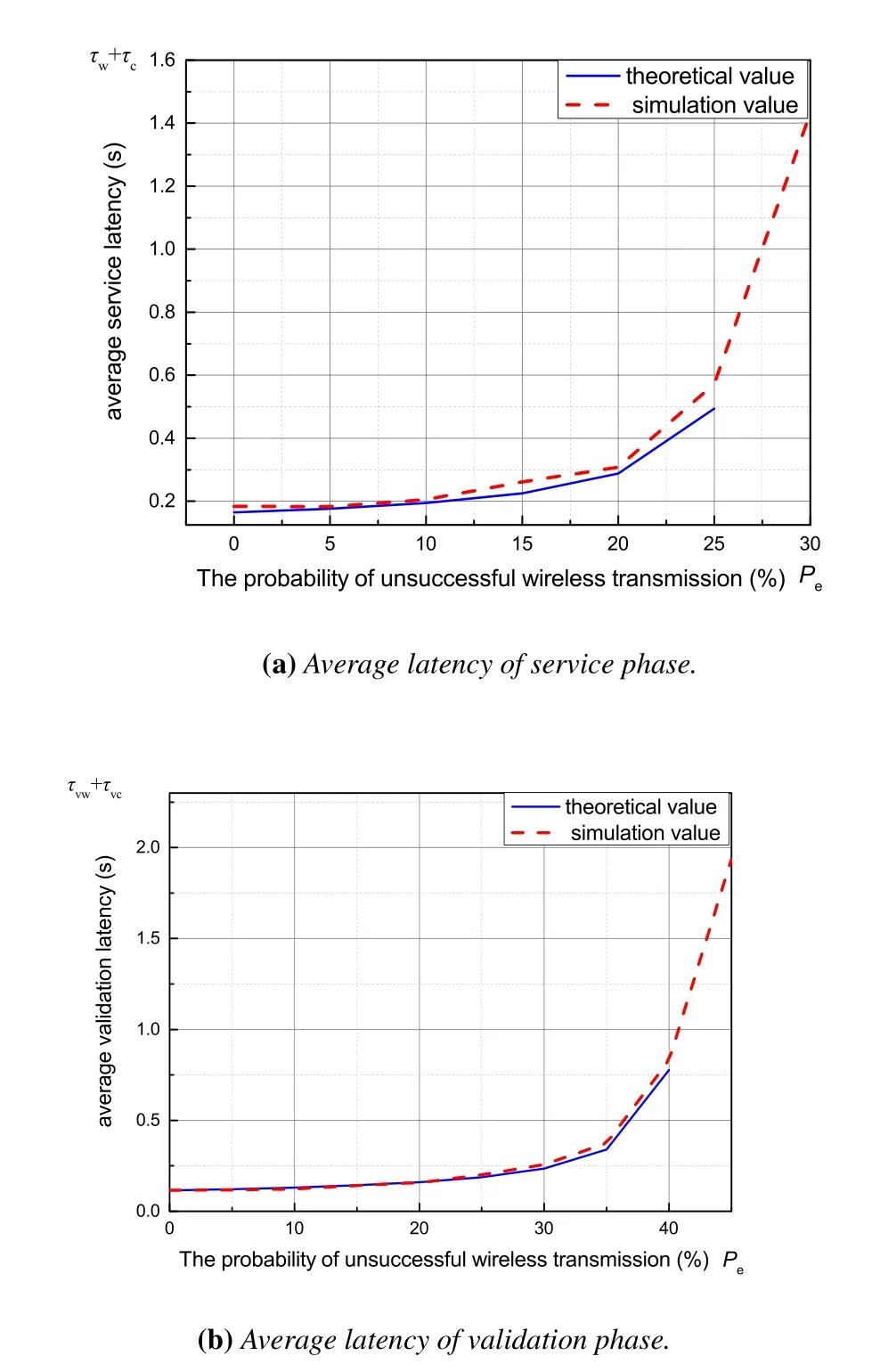
Figure 7.Average latency vs. the probability of unsuccessful wireless transmission Pe.

Taking Figure7(a) for example,whenPeincreases from 20% to 25%,the equivalent wireless transmission service rate in the service phaseKs(1-Pe)µwis decreased from 566 tasks/s to 531 tasks/s,which is close to the critical value of the stability condition of queuing systemρw=≤1.Thus,the growth rate of average latency increases.WhenPe=30%,the equivalent wireless transmission service rate is 495 tasks/s,and the queuing system is no longer stable.We cannot obtain a positive analytical latency,and simulation results show a huge increase in average latency.Results in other figures also have such inflection points of average latency,which reflect the critical values of the stability condition of queuing systems too.

The optimal system deployment solution is also verified by simulations,and system parameters are givenin Table 2.We first calculate the theoretical optimal system deployment according to Algorithm 1,and all the temporary value ofKs,µw,µc,Kv,µvw,µvcandFin the iterative solution process are recorded.These theoretical values are used to draw the solid blue line in Figure 8.These values of(Ks,µw,µc,Kv,µvw,µvc)are also used for simulation,and the simulated values of ˆFare obtained and are used to draw the red dashed line in Figure 8.Results show that the theoretical and simulation values match very well.We also obtained the optimal solution ofand list them in Table 3.

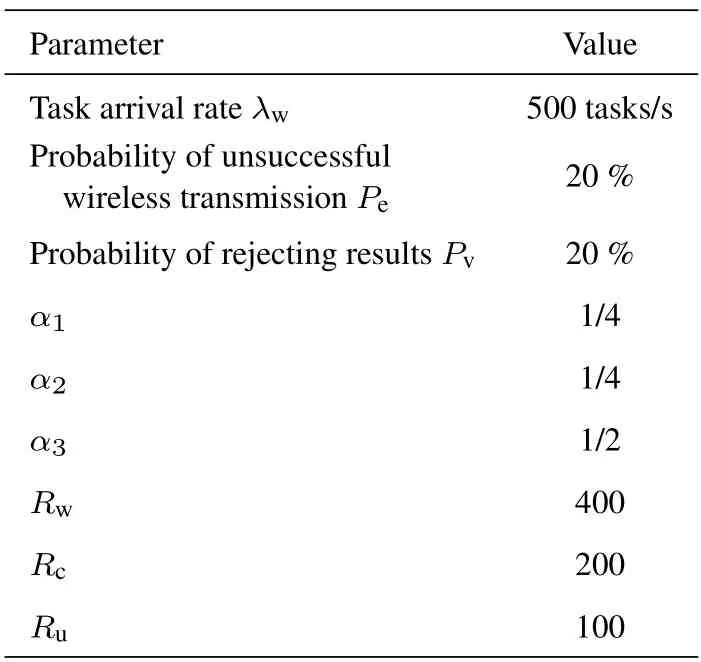
Table 2.System deployment optimization parameters.

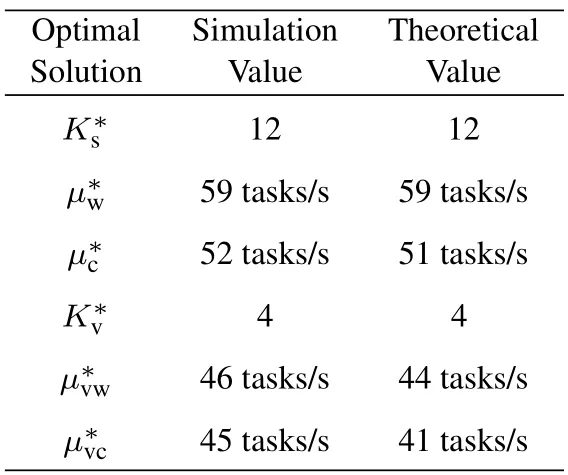
Table 3.Optimal simulation results.

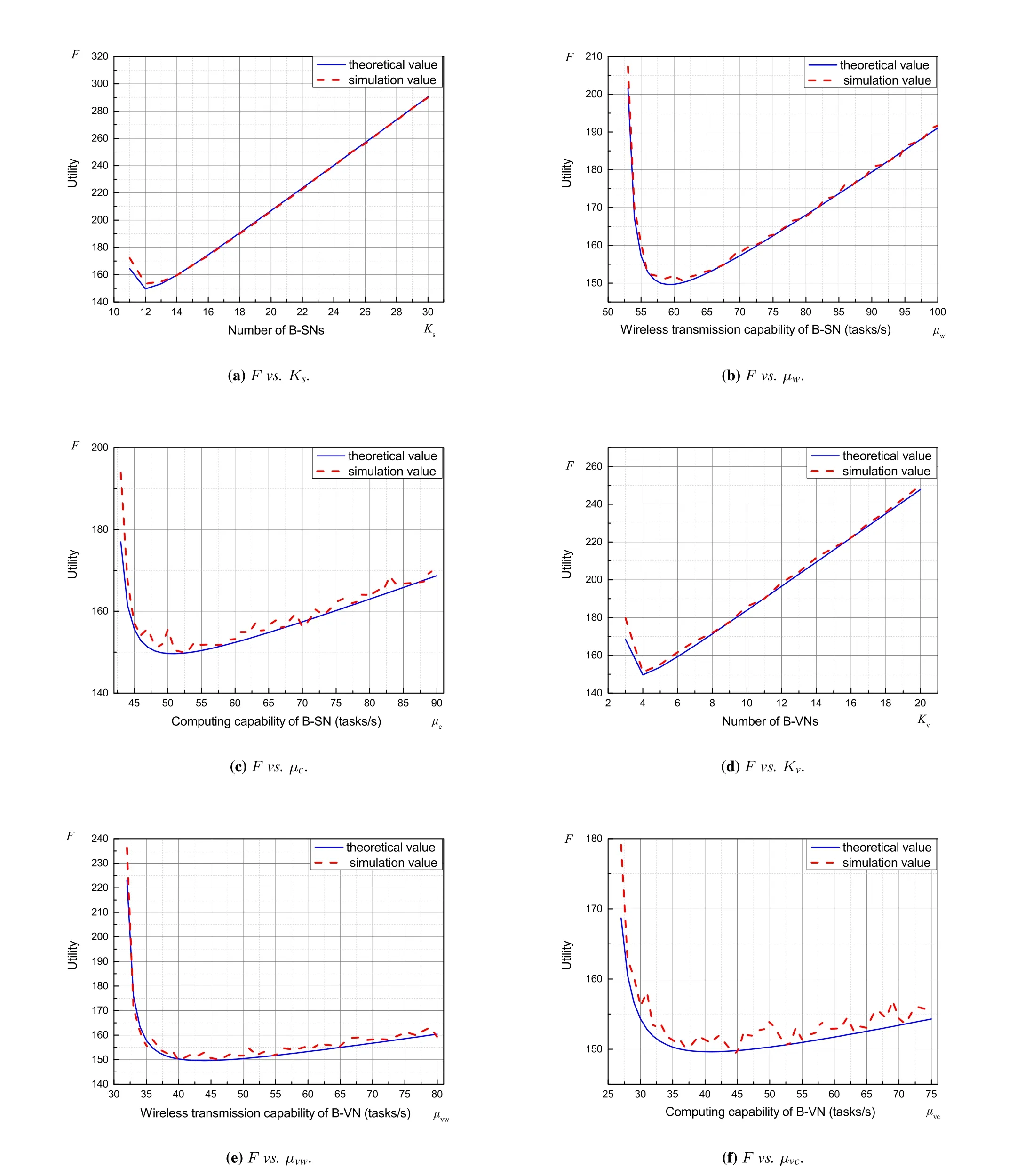
Figure 8.System utility vs. varying system parameters.

5.2 System Deployment Parameter Calculation

Using the verified analytical results,we calculated the optimal system deployment parameters with varying task arrival rates and system utility weights.

When the system utility weights are set as the same value in a group of simulations,the results with varying task arrival rates are given in Table 4.Obviously,with the increase ofλw,the number of B-SNs and BVNs is increased,and the required wireless transmission capabilities and computing capabilities of each BS are also increased.However,this increase is not the strict linear growth as the resource utilization rate reflected byρw,ρc,ρvwandρvcis increasing.That is to say,when the task arrival rate is large,the system tends to configure the resources more efficiently to save cost.

Table 4.System deployment parameters with(α1=,α2=,α3=).

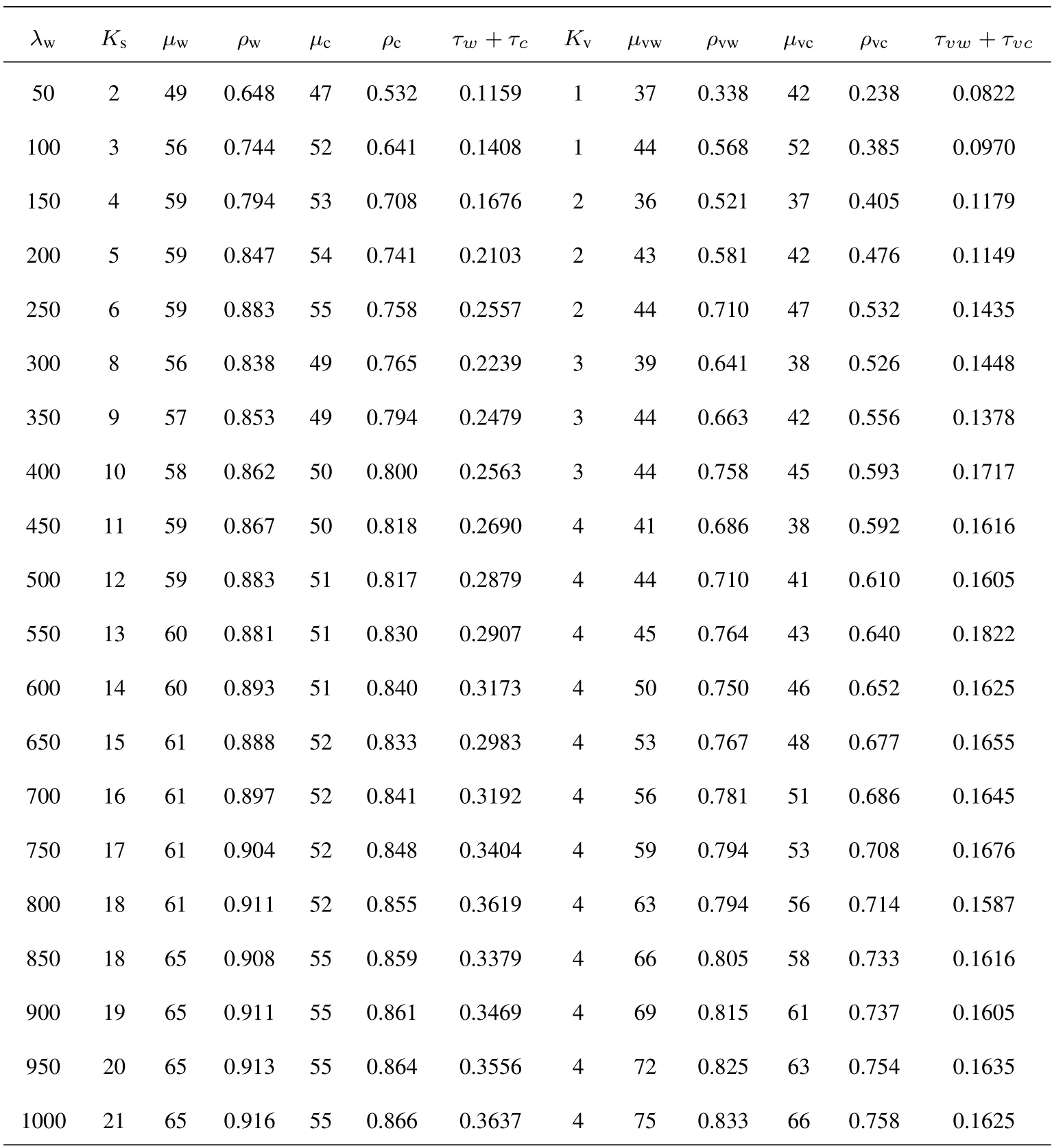
Table 4.System deployment parameters with(α1=,α2=,α3=).

The results with varying system utility weights arealso compared in Table 4,Table 5 and Table 6.From Table 4 to Table 6,the weightα3of the latency penalty decreases,which means the main concern of the system design changes from providing better service performance to saving the system deployment cost.Calculation results show that the designed number of BSNs is greatly reduced to reduce the cost when the task arrival rates are the same.Although the transmission service rateµwof each B-SNs increases to ensure the stability of the system,the overall service rate is slightly reduced with the decreasing ofα3.Accordingly,the latency shows an increasing trend on the whole.It is also worth noting that the utilization of the system service capabilities increases with the decreasing ofα3.This means the proposed optimization scheme is aware of that the main concern is saving the system deployment cost and adapts the system configuration to the design objective.

Table 5.System deployment parameters with(α1=,α2=,α3=).

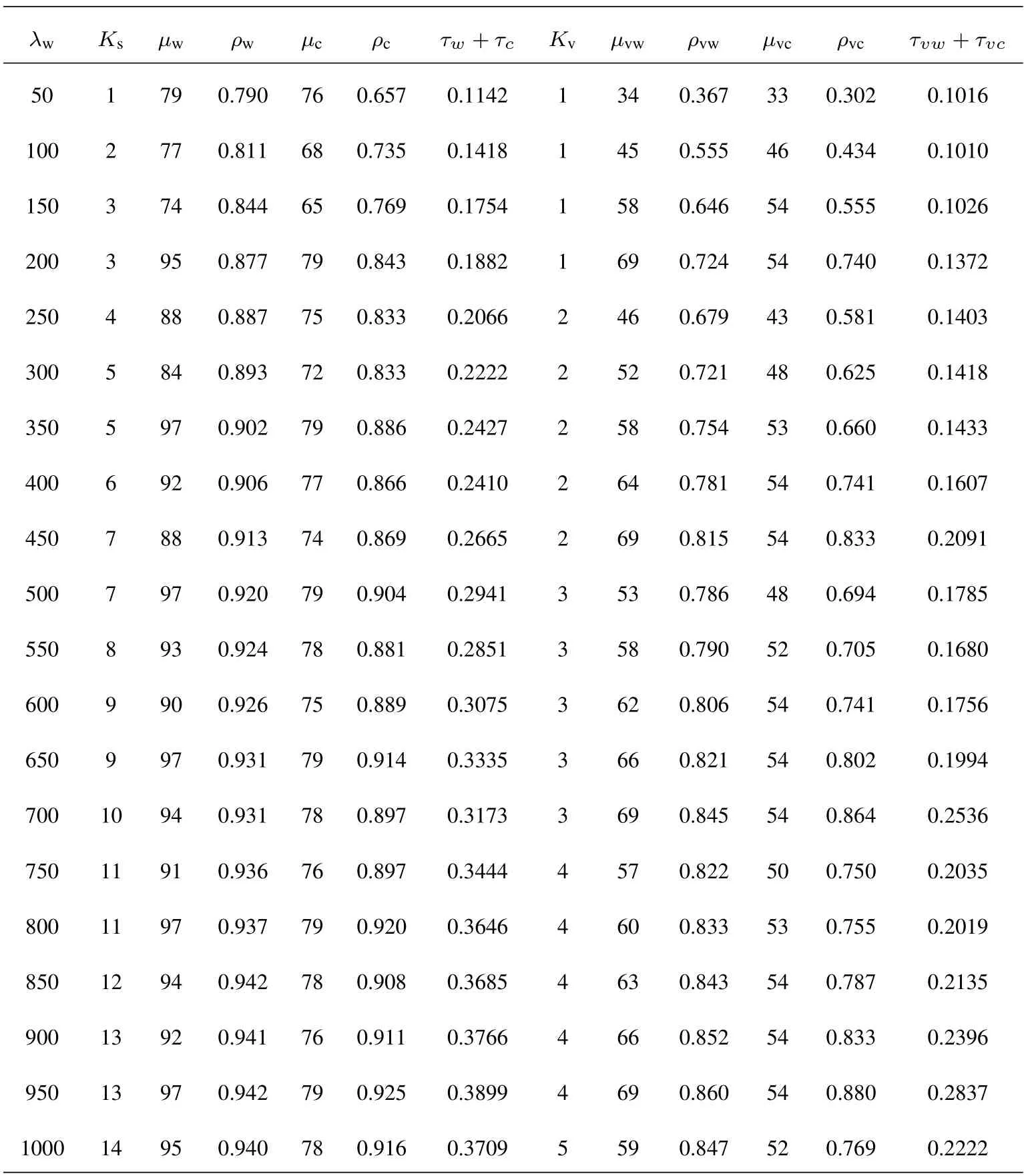
Table 5.System deployment parameters with(α1=,α2=,α3=).

Table 6.System deployment parameters with(α1=,α2=,α3=).

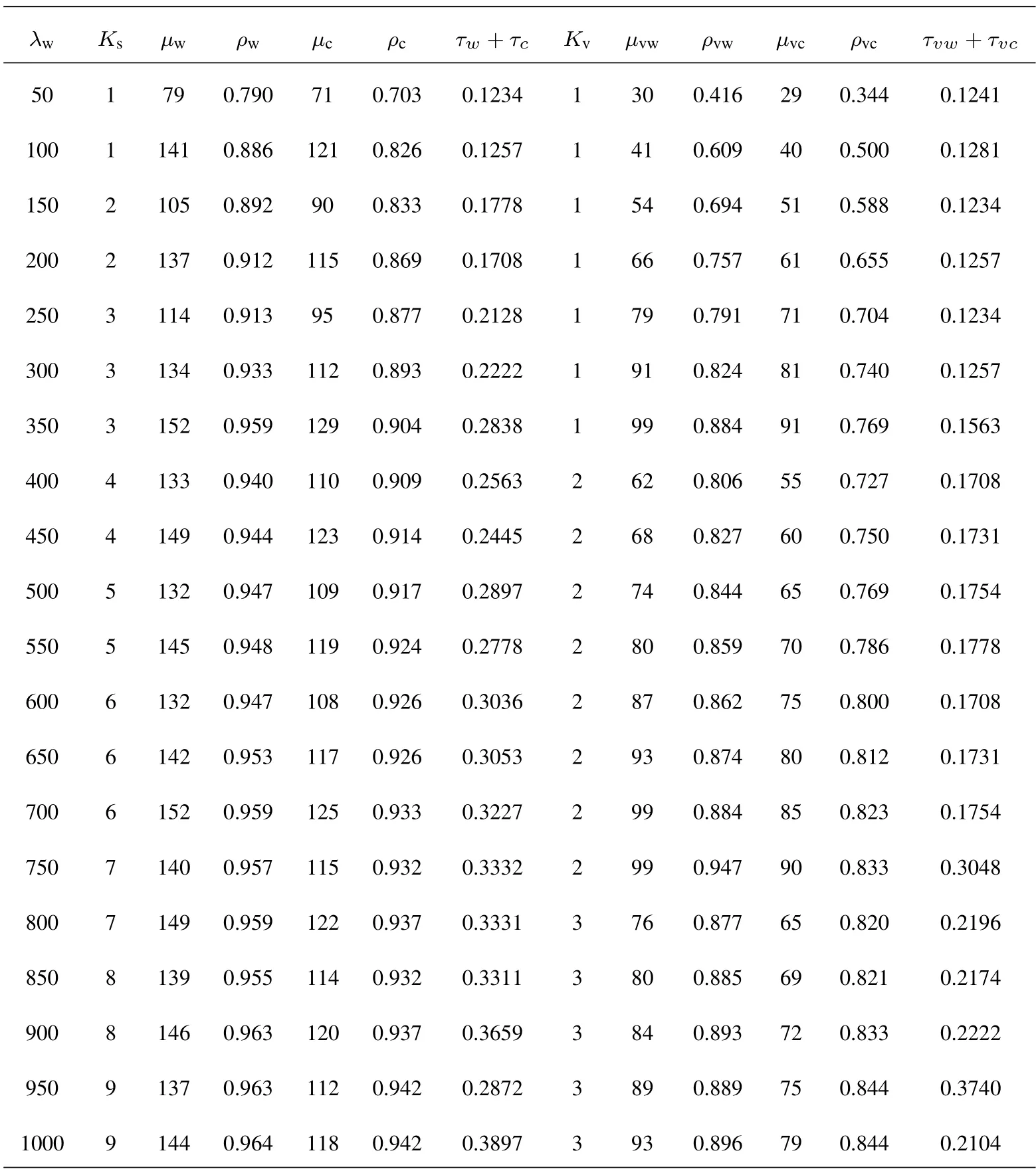
Table 6.System deployment parameters with(α1=,α2=,α3=).

VI.CONCLUSION

In this paper,the application-oriented task validation procedure in the blockchain-enhanced UDN is designed in smart contracts.The latency of the whole service and validation process is analyzed with the consideration of the wireless re-transmission and the probability of malicious deception by users.The system optimization problem,which minimizes the costs of BSs,MEC servers and latency,is modeled andsolved by the classical convex optimization algorithm.Numerical results verify our analysis.Further,the optimized system deployment results show that with the increase of task arrival rate,the system tends to configure the resources more efficiently to save cost.When the weight of the latency penalty decreases,the resource utilization rate increases to reach the best balance between latency performance and system deployment cost.