A Construction Method of Arbitrary-Length Polar Codes
Xiaojun Zhang ,Chengguan Chen ,Rongcai Zhang ,Jianming Cui ,Qingtian Zeng
1 Shandong University of Science and Technology,Qingdao 266590,China
2 State Key Laboratory of High-End Server and Storage Technology,Jinan 250101,China
*The corresponding author,email: zhangxiaojun@sdust.edu.cn
Abstract: To remove the restriction on code length of polar codes,this paper proposes a construction scheme,called stepwise polar codes,which can generate arbitrary-length polar codes.The stepwise polar codes are generated by sub-polar codes with different code lengths.To improve coding performance,sub-polar codes are united by polarization effect priority algorithm,which can reduce the number of incompletely polarized channels.Then,the construction method of the generator matrix of the stepwise polar code is presented.Furthermore,we prove that the proposed scheme has lower decoding complexity than punctured,multi-kernel polar codes.Simulation results show that the proposed method can achieve similar decoding performance compared with the conventional punctured polar codes,rate-compatible punctured polar code,PC-short and asymmetric polar codes(APC)when code length N=48 and 72,respectively.
Keywords: code construction;polar codes;arbitrarylength;channel polarization;union encoding
I.INTRODUCTION
Polar code is a new class of channel code which achieve capacity with low encoding and decoding complexity.Many improved codec implementations are proposed to enhance error correction performance and reduce latency,such as the reduced latency softcancellation (RLSC) algorithm in [1] and the Belief propagation(BP)decoder in[2].But these algorithms are based on the precondition that polar codes are constructed by the Kronecker product of the 2 × 2 kernel matrix [3].Hence that the code length of polar codes is limited to powers of two,which restricts the application range of polar codes.Many efforts have been made to remove the restriction on code length[4–7].At present,there are two main solutions [8].The first is the punctured polar code,which was first proposed in[9].Then Chen Kai et al.proposed the ratecompatible punctured polar (RCPP) code to improve the performance[10].Dong-Min Shin et al.proposed a scheme of constructing a punctured polar code by reducing a generator matrix[11].Later,Runxin Wang et al.improved this method and obtained better coding effect in [12].Wang Tao et al.proposed Paritycheck-concatenated(PCC)polar codes with better performance under the condition of short codeword code and low code rate to generalize the cyclic redundancy check (CRC) concatenated polar codes [13] and then a greedy optimization with low search complexity is proposed for the transmission order of the punctured code bits [14].Jang et al.show that binary domination completely determines incapable or shortened bit patterns for polar codes,and that all the possible incapable or shortened bit patterns can be identified [15].Afterwards they proposed a structural way of extending polar codes [16],the results show that it is more competitive in terms of performance and implementation complexity.However,although the code length of the punctured polar code is reduced,the decoding complexity is still equal to the decoding complexity of the mother code,that is,the average complexity of each bit is increased.
The second is multi-kernel polar code [17–19].Arikan conjectured that the polarization phenomenon is not restricted to the powers of the kernelT2.When the kernelsTlwithl>2,the polarization effect still exists and it has been proven in[20].[21]proposed a ternary kernel decoder and extended the code length to 3n.Then,Presman et al.proposed a non-binary kernel-polar code,but the code length is still limited to the power of the kernel lengthlin [22].In 2016,Frederic Gabry et al.utilized a variety of kernels to construct polar codes for the first time,and the polar code generator matrix was changed toGN≜Tn1⊗···⊗Tns.It expanded the code length of polar code to the non-prime field and achieved a better decoding performance [23].However,the code length of multi-kernel polar codes is still limited and the complexity is high [24].Dong-Min Shin et al.suggest using punctured method on multi-kernel polar codes[11],but it will reduce the performance of multikernel polar codes.In [25],W.J.Gross et al.proposed a new low-complexity asymmetric polar codes(APC),which is a flexible polar coding scheme that exhibits block length-dependent decoding complexity with similar error correction performance to the stateof-the-art coding schemes.
In this paper,we propose a new construction scheme for arbitrary-length polar codes.Different from traditional polar codes,the encoding of stepwise polar codes is divided into two steps,sub-code encoding and union encoding.At the decoding,the first step is sub-code union decoding and the second step is subcode decoding.In order to improve the coding performance and reduce the defect of short sub-codes,a polarization effect priority (PEP) algorithm to construct a union coding scheme is proposed.Furthermore,a modified decoding algorithm is presented.The PEP algorithm can increase the polarization effect of incompletely polarized channel and lower the block error rate (BLER) while ensuring the number of information bits.In addition,we analyze the decoding complexity of stepwise polar codes and punctured polar codes.The simulations show that the complexity of stepwise polar codes is lower than punctured polar codes and multi-kernel polar codes.Meanwhile,the proposed method can obtain better decoding performance.
The rest of this paper is organized as follows.In Section II,we review the polar code and successive cancellation(SC)decoding algorithm.Section III proposes the construction of a stepwise polar code and the encoding and decoding algorithms.In Section IV,we analyze the complexity of stepwise polar codes.The performance analysis is illustrated in Section V.Section VI concludes this paper.
II.PRELIMINARIES
2.1 Polar Codes
Polar code is a linear block code based on channel polarization theory [3].Channel polarization is divided into two phases,channel combining and channel splitting.With the increase of code length,the capacity of some sub-channels tends towards 1,while the remaining sub-channels tends to 0.Polar code transmits information bits onKsub-channels with the capacity tending to 1,transmitting frozen bits on the remaining sub-channels.
Given a binary-discrete memoryless channel (BDMC)W:X-→Ywith input alphabetX={0,1}and output alphabetY.W(y|x) is the channel transition probabilities withx∈Xandy∈Yand the corresponding reliability metric can be measured by Bhattacharyya parameter.
According to[3],the Bhattacharyya parameters can be simplified to(2).
By using of the channel polarization,the polar coding can be described as follows.
Given the code lengthN,the information lengthKand code rateR=K/N.The input vectorcan be encoded into a codewordby
where the matrixGNcan be recursively defined asdenotes the 2×2 kernel matrix,and⊗ndenotes then-th Kronecker product.The encoder is illustrated in Figure 1.
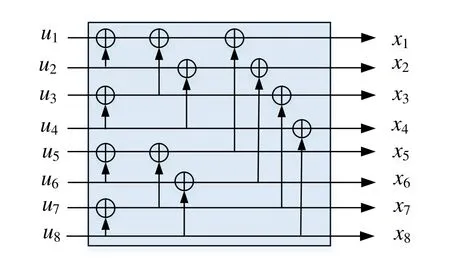
Figure 1.The encoder of polar code for N=8.
2.2 Successive Cancellation Decoding
Forn>0,letTndenote the full binary tree of depthn,as illustrated in Figure 2.
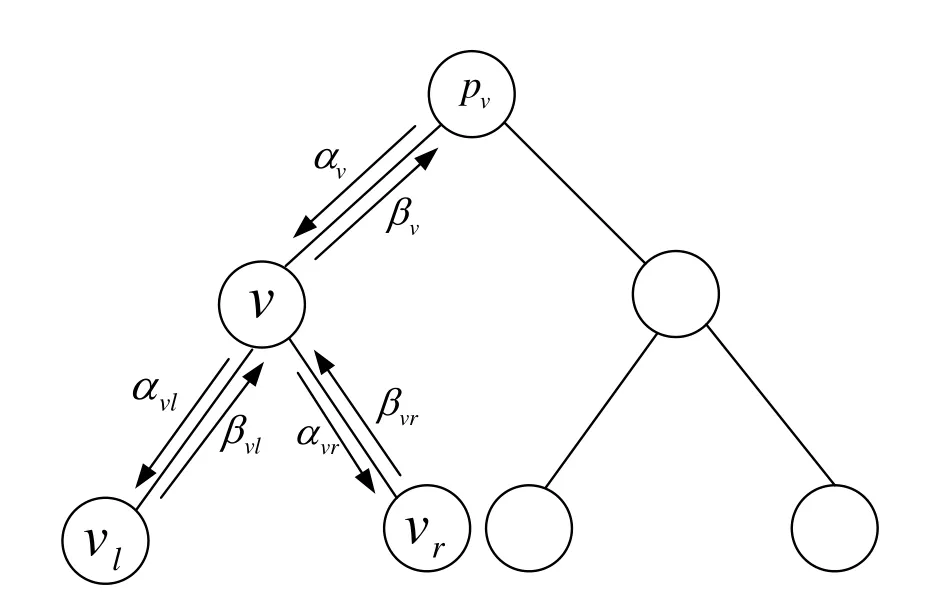
Figure 2.The decoder of node v.
Give a nodev∈[Tn],Lv(i)represents thei-th leaf of the nodev.αvandβvrefer to soft inputs and outputs ofvrespectively.In depth-first traversal of the decoding tree,vlandvrdenote the left child and right child ofvrespectively.we obtainαvlas
Compute theαvrby
Finally,βvcan be calculated as
III.STEPWISE POLAR CODES
3.1 Construction of Stepwise Polar Codes
Any positive integer can be converted to a binary representation.When a polar code with code lengthNis not a power of 2,we can decomposeNintoiitems and any item is a power of 2.Therefore,when the polar code is composed byishorter polar codes with different code lengths,the arbitrary-length polar codes are obtained,and shortcomings of limited code length can be solved.Based on this,we propose a stepwise polar codes.As shown in Figure 3,it consists of a series of sub-polar codes with different code lengths.
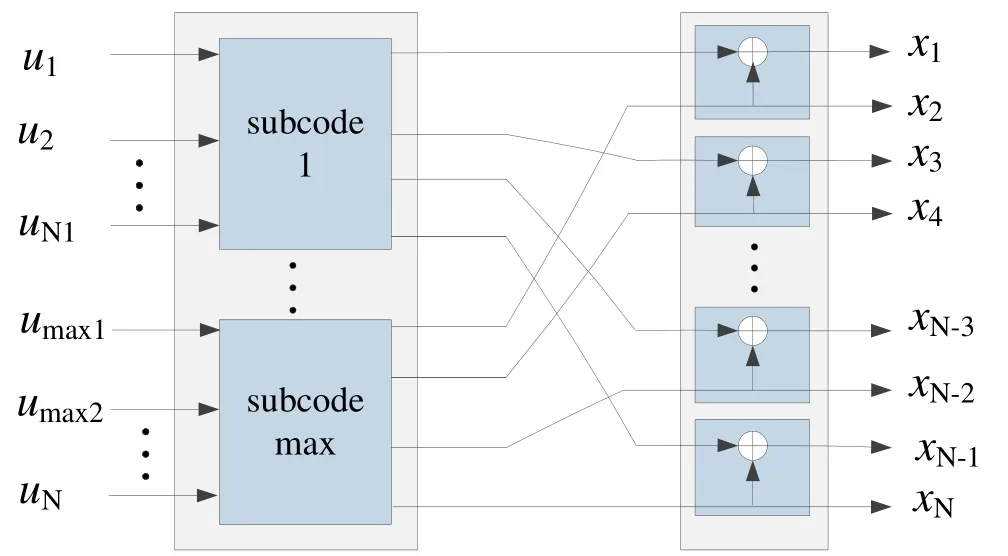
Figure 3.The structure of the stepwise polar code.
As illustrated by(7),the length of sub-codes can be obtained byNb,whereNbis binary representation ofN.For instance,ifN=13,Nb=[1 1 0 1],then sub-codes length ofNare 8,4 and 1.Let Nmaxbe the length of the maximum sub-code,then Nmax=8.Obviously,all sub-code lengths conform to the requirements of binary kernel polar codes and the length of maximum sub-code(the sub-code with largest code length)N/2≤Nmax≤N.When we construct a stepwise polar code with code lengthNand code rateR,the following steps are performed.
1.Nis converted to binary numberNbto get the length of sub-codes.
2.All the sub-codes are sorted according to the code length,and theI(W) of the sub-channels in subcodes is calculated according to(2).
3.Design a union coding scheme,select the subchannel of the maximum sub-code and the subchannel of other sub-codes according to Algorithm 1 to polarize.
4.Calculate theI(W) of stepwise polar code by union coding scheme,and selectKsub-channels based onI(W)to transmit information bits.
It can be observed that some sub-codes of the stepwise polar code are short and the polarization rate is low.To tackle this issue,the polarization effect priority algorithm is proposed as follows.
1.Letε=[ε1,ε2,···,εN-1,εN] denote the channel sequence,whereI(Wε1)≥I(Wε2)≥···≥I(WεN-1)≥I(WεN).Select topKsub-channels of all sub-codes with largerI(W) and letIavg=
2.Letε′=be the subchannels of maximum sub-code are sorted byI(W)in ascending order.Lgs=|εA|,whereεA⊂εε′andI(WεA)>Iavg.

3.Letε′′=be sub-channels of all non-maximum sub-codes are sorted byI(W)in ascending order,too.
4.InputLgsinto the following Algorithm 1 and obtain the results.In Algorithm 1,represents thesubchannel of the maximum sub-code and thesubchannel of non-maximum sub-codes are mutually polarized.The PEP algorithm getLgsbased onK.This leads to the stepwise polar codes with same lengthNbut different code rates has different structure.The channel structure diagram of Algorithm 1 is shown in Figure 4.
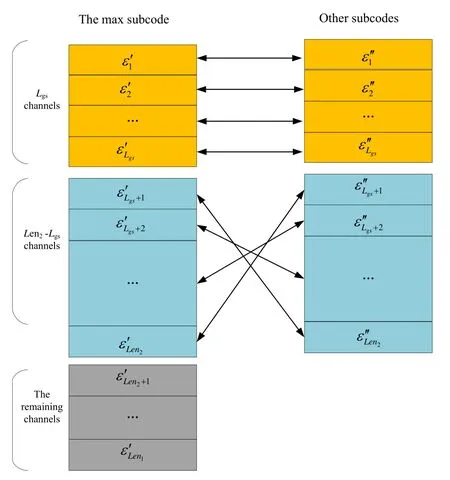
Figure 4.Channel structure diagram of algorithm 1.
3.2 Encoding and Decoding of Stepwise Polar Codes
The encoding of a stepwise polar code can be determined by its generator matrixGNand its frozen bits.It is also applicable to(3).The frozen bits of the stepwise polar code has already been determined at the time of construction.Therefore,we only need to get the generator matrixGNof the stepwise polar code.The stepwise polar code is composed by sub-code and union encoding,so its generator matrixGNis composed of sub-code generator matrixGNi,zero matrix and union coding scheme matrixGUS.The specific construction method is as follows and the structure is depicted as Figure 5.
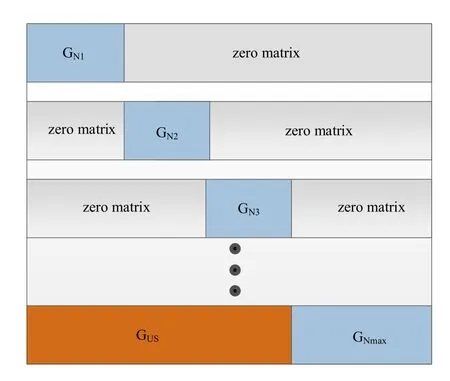
Figure 5.Generator matrix of stepwise polar codes.
According to the union coding scheme,if thei-th sub-channel of the non-maximum sub-codejand thek-th sub-channel of the maximum sub-code are mutually polarized,thei-th column of the union coding matrixGUSis the same as thek-th column of the maximum sub-code generator matrix.Traversing the channels of all non-maximum sub-codes,the union coding matrixGUScan be obtained.
The sub-code generator matrixGNiis arranged on the diagonal ofGN,and the maximum sub-code generator matrixGNmaxis in the lower right corner.
The decoding of the stepwise polar code is divided into two steps.The first step is union decoding.The receivedLLRis decoded according to(8),and it’s corresponding to the union encoding.The result of the union decoding is transmitted to the corresponding sub-code.The sub-codes are applicable to the polar code decoding algorithms,such as[1],[13]and[17].
For instance,we construct stepwise polar codes with code length 14 and code rate 0.5 as follows.
1.Get sub-codes:Nb=dec2bin(14)=1110.Then,we get three sub-codes with code lengths ofN1=21,N2=22andNmax=23,respectively.
2.Calculate the channel capacity of sub-channels of each sub-code: Get theI(W)according to (3).
3.Design a union coding scheme: Based on the results obtained in the previous step,designing a union coding scheme by PEP algorithm,the structure is depicted as Figure 6.
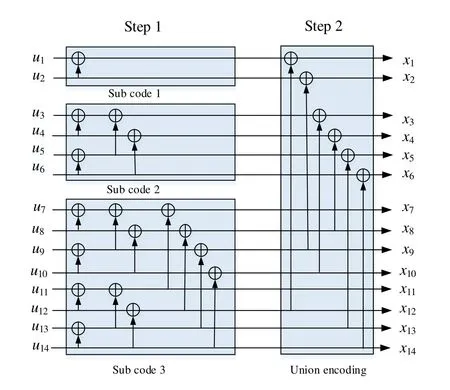
Figure 6.The structure of stepwise code(N=14).
4.Get generator matrix: The generator matrix of stepwise polar codes is composed of sub-code matrixG2,G4,G8and union coding matrixGUS,as shown in Figure 7.

Figure 7.Generator matrix of stepwise polar code(14,7).
IV.COMPLEXITY AND CAPACITY OF STEPWISE POLAR CODES
4.1 Complexity of Stepwise Polar Codes
The SC decoding complexity of polar code isO(NlogN)[1].As the code length increases,the complexity will also increase,which will have a great impact on the latency.A disadvantage of the punctured polar code is that when the code length is reduced fromNtoM,its decoding complexity does not drop.This shows that the decoding complexity of each bit of a punctured polar code is more than that of its mother code.In the decoding,most of the operations are used to calculate(5).We consider each operation of the(5)as a processing element (PE),then the number of PE can reflect the decoding complexity.
LetMbe the length of the code after puncturing,Ndenote the length of the mother code.Then,the number of PE in the punctured polar codes can be represented by(9).
The number of PE in the multi-kernel(T2andT3)polar codes is indicated by(10),under the code lengthM=NT2*NT3.NT2andNT3are related to the construction of multi-kernel polar code.For instance,M=72=2*2*2*3*3,then,NT2=2*2*2,NT3=3*3.
And PE in the stepwise polar codes under the same code lengthM(k=dec2bin(M))is indicated by(11).
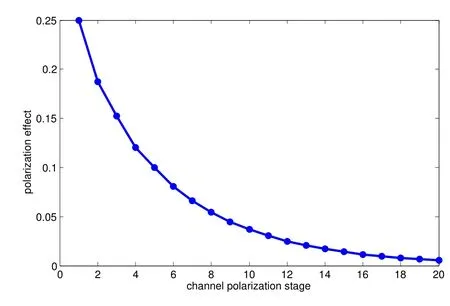
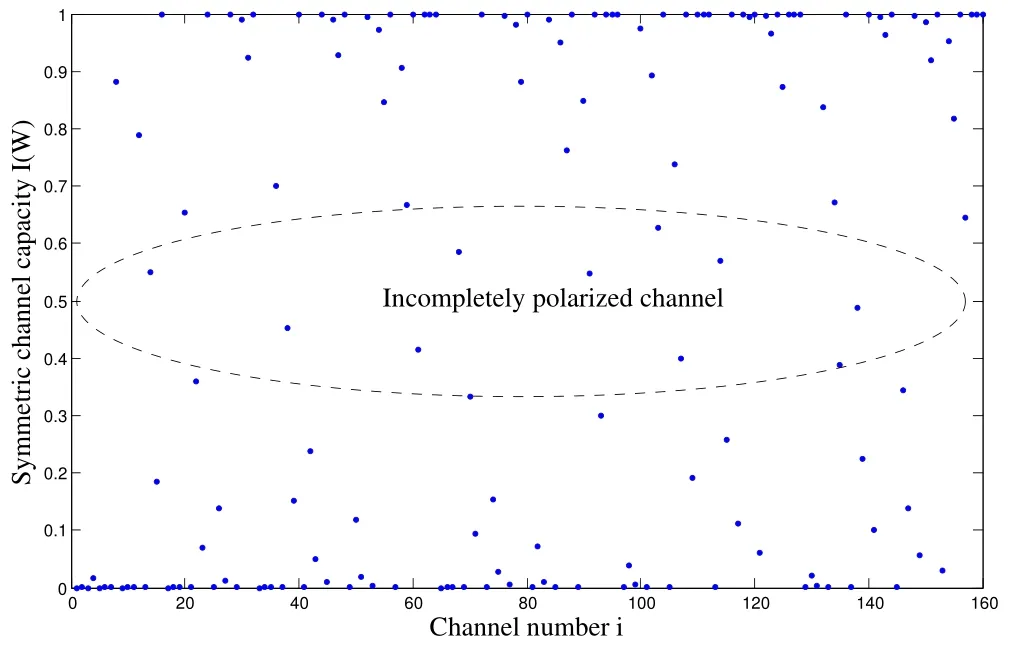
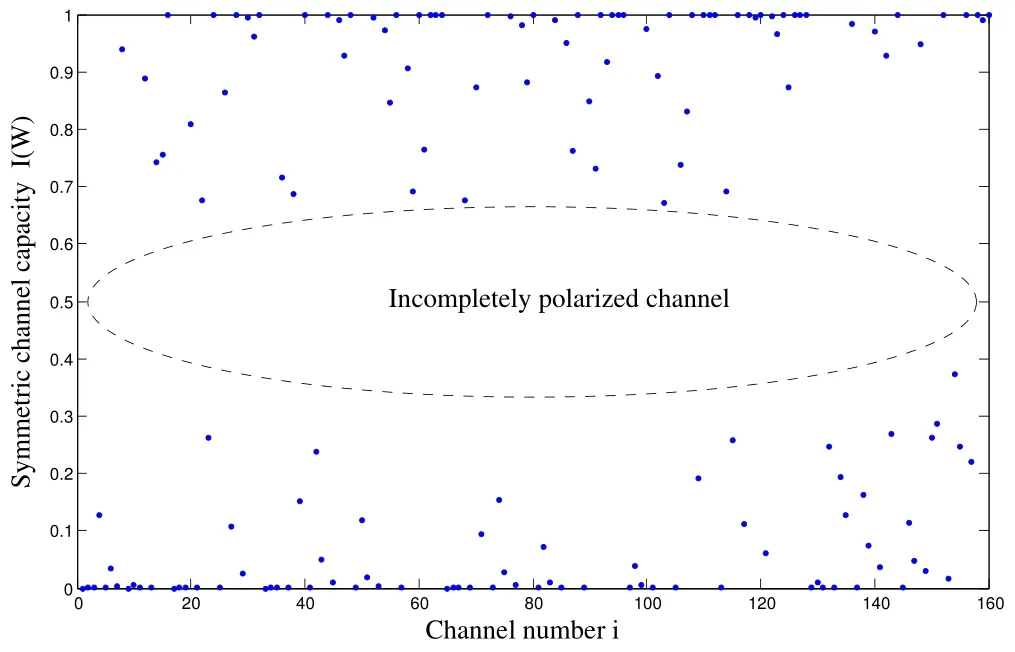
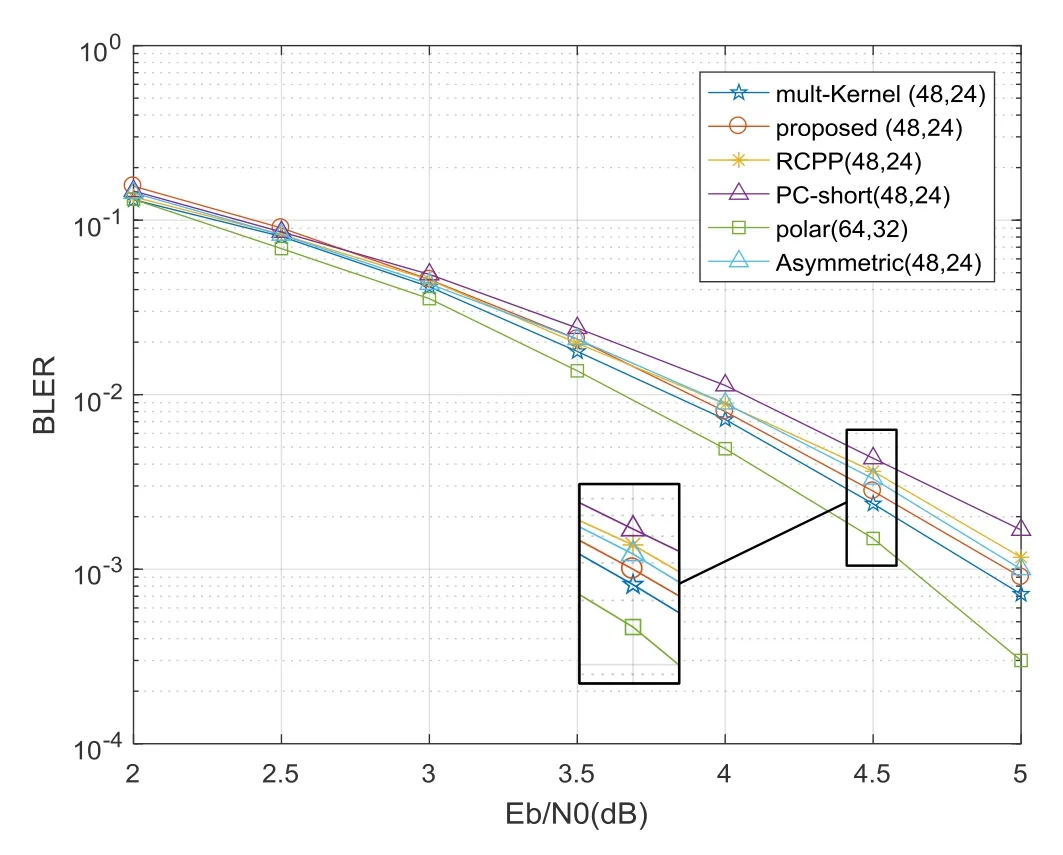
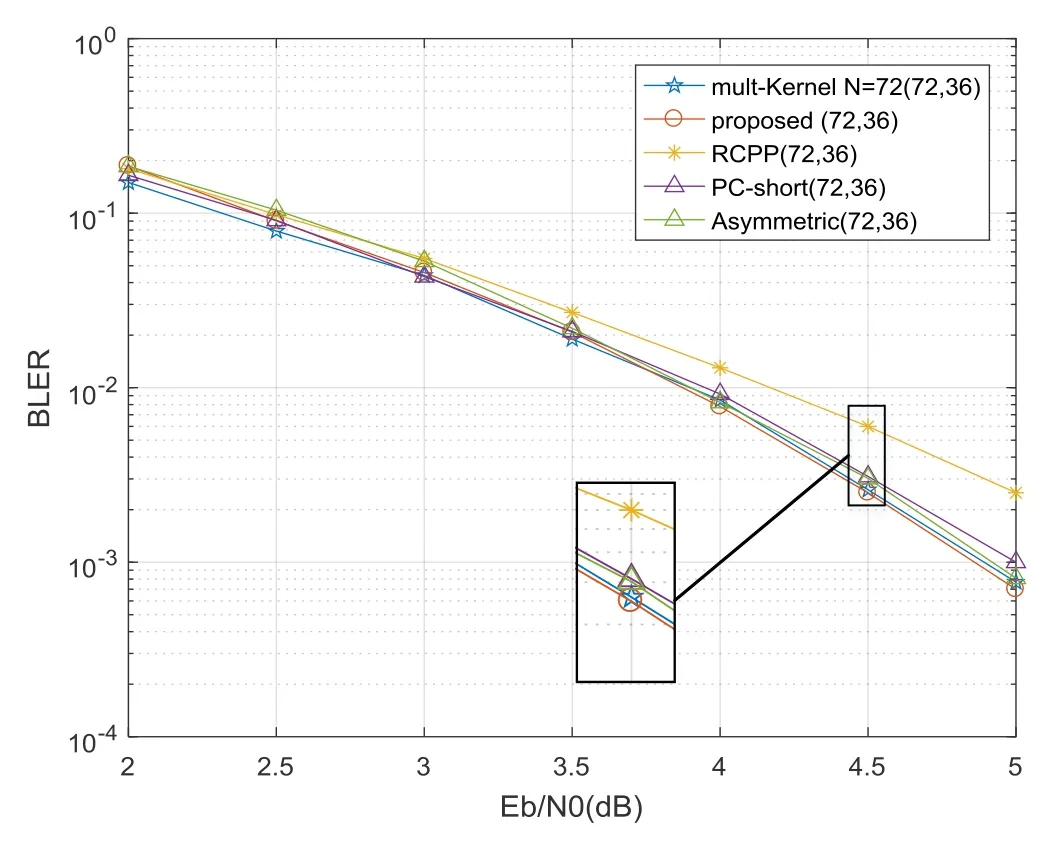
From (9) and (12),we can see that the value ofis positively correlated withM,andis a constant value when 0.5*N Obviously,we can get Therefore,the decoding complexity of the stepwise polar code is less than that of punctured polar code. Figure 8 shows that the PE number of the stepwise polar code is approximately linear with the code length,the PE number of the punctured polar codes is step-incremental,same as the original polar codes.When the code length is slightly larger than half of the length of the mother code,the PE number of the stepwise polar codes is about 50% lower than that of the punctured polar codes.As the code length approaches the mother code length,the difference in PE number gradually decreases.The PE number of multikernel polar codes are lower than that of punctured polar codes,but it is also higher than that of stepwise polar codes. Figure 8.Complexity of punctured,multi-kernel and stepwise codes. According to[21],once there is a codeword bit is not transmitted,the reliability of all the splitting channels will be reduced,and the capacity of some splitting channels will even be degraded to zero.Moreover,after several channel polarizations,the effect of each polarization is gradually reduced,which will increase the BLER of the polar code.The reason is that the subchannels are mutually polarized with their own symmetrical channel. Lemma 1.Inthebinaryerasurechannel(BEC),the polarizationeffectisdegressive.Whenthechannel capacitytendstoward1or0,thepolarizationeffect isalmost0. Proof.According to(2),we can get As the channel polarization increases,the number of channels whose capacity tends to 0 or 1 increases,and the polarization effect becomes lower and lower.According to[3],the average channel capacity changeP(s)represents the polarization effect at each stage follows Figure 9 shows theP(s)of each stage of polar code.As the stage increases,P(s)becomes lower and lower.After the first stage,P(1)=0.25.By the last stage,P(20) tended to 0.Different sub-channels can be selected to polarize each other in the union coding stage,and the polarization effect can be improved effectively.Polar code transmits information bits on sub-channels that have higherI(W).But,if code rateRis large,some incompletely polarized channels with lowerI(W) are selected to transmits information bits.According to the PEP algorithm,different channels are selected for mutual polarization.Under the condition of ensuring the number of information bits,the number of incompletely polarized channels can be reduced and the decoding performance can be optimized.The number of incompletely polarized channels of stepwise polar codes is less than that of punctured polar codes,as shown in Figure 10 and Figure 11. Figure 9.Polarization effect of each stage of polar code. Figure 10.The channel capacity of punctured polar codes. Figure 11.The channel capacity of stepwise polar codes. In this section,we compare the BLER of proposed scheme,PC-short[12],RCPP[10],multi-kernel polar codes[23]and Asymmetric Construction[25]via simulations over Binary-Input Additive White Gaussian Noise channels (BI-AWGNs).The sub-code decoding adopts SC and Successive Cancellation list(SCL)with L=2 decoding algorithms.We set the maximum number of frames as 106,and simulation results are shown in Figure 12 and Figure 13. Figure 12.BLER performance comparisons(48,24). Figure 13.BLER performance comparisons(72,36). We compared different codes with length 72 and 48.For the stepwise polar code withN=48,we use two sub-polar codes with code length of 32 and 16.Figure 12 shows that the proposed method has performance strength compared to RCPP,Asymmetric and PC-short whenEb/N0>3dB.For the stepwise polar code withN=72,we use two sub-polar codes with a code length of 64 and a code length of 8.As shown in Figure 13,for the (72,36) polar code,when SC is evaluated,the proposed algorithm slightly outperforms multi-kernel,PC-short and Asymmetric but is inferior to RCPP.When SCL(L=2)is adopted,the multi-kernel has the least decoding performance.The proposed algorithm,RCPP and Asymmetric show very similar performance and outperform the PC-short.Meanwhile the proposed is performing better than RCPP in lowEb/N0regions. In this paper,we propose a method to construct arbitrary-length polar codes by concatenating short sub-codes and detail the encoding and decoding algorithms.Through uniting sub-channels and selecting frozen bits by PEP algorithm,the effectiveness of the proposed method is improved.We prove that complexity of proposed method is less than the punctured and multi-kernel polar codes.Numerical results show that the proposed decoding performance can be equal to or exceed that of the existing method of arbitrarylength polar codes. This work was supported in part by Joint Fund for Smart Computing of Natural Science Foundation of Shandong Province (ZR2019LZH001),Shandong University Youth Innovation Supporting Program(2019KJN020,2019KJN024),Shandong Key Research and Development Project (2019GGX101066),the Taishan Scholar Program of Shandong Province,the Natural Science Foundation of China(61701284).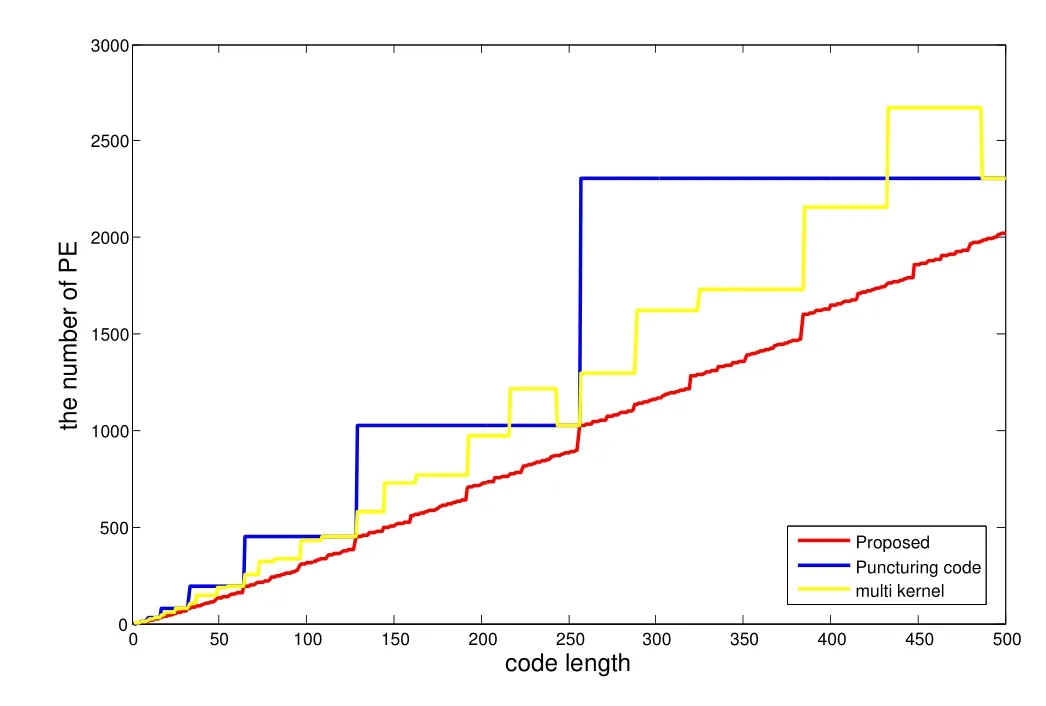
4.2 Polarization Effect of Stepwise Polar Code
V.SIMULATION RESULTS
VI.CONCLUSION
ACKNOWLEDGEMENT
- China Communications的其它文章
- SR-DCSK Cooperative Communication System with Code Index Modulation: A New Design for 6G New Radios
- Sparsity Modulation for 6G Communications
- Sparse Rev-Shift Coded Modulation with Novel Overhead Bound
- Reconfigurable Intelligent Surface-Based Hybrid Phase and Code Modulation for Symbiotic Radio
- Model-Driven Deep Learning for Massive Space-Domain Index Modulation MIMO Detection
- Modulation Recognition with Frequency Offset and Phase Offset over Multipath Channels

