Sparse Rev-Shift Coded Modulation with Novel Overhead Bound
Mingjun Dai ,Wanru Li ,Chanting Zhang ,Xiaohui Lin,* ,Bin Chen
1 School of Computer Science and Technology,Kashi University,Kashi 844000,China
2 College of Electronics and Information Engineering,Shenzhen University,Shenzhen 518000,China
*The corresponding author,email: xhlin@szu.edu.cn
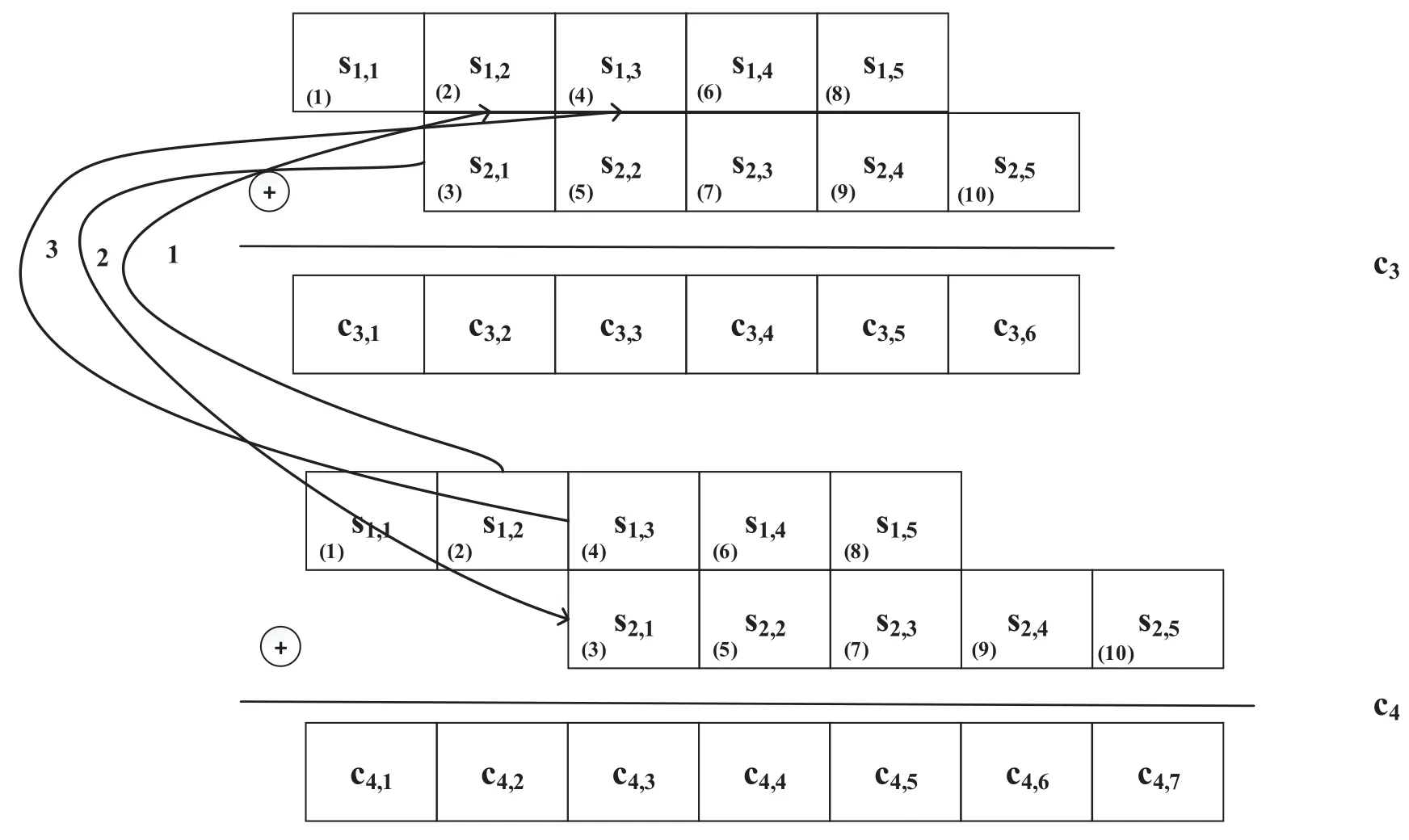
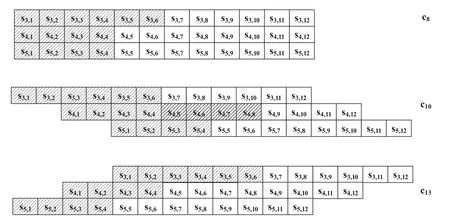
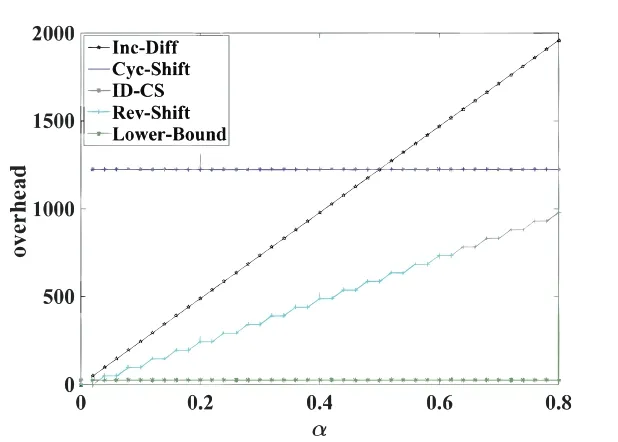
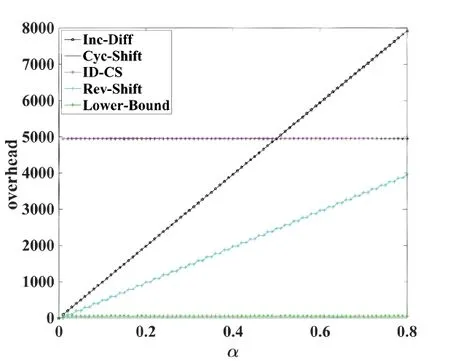
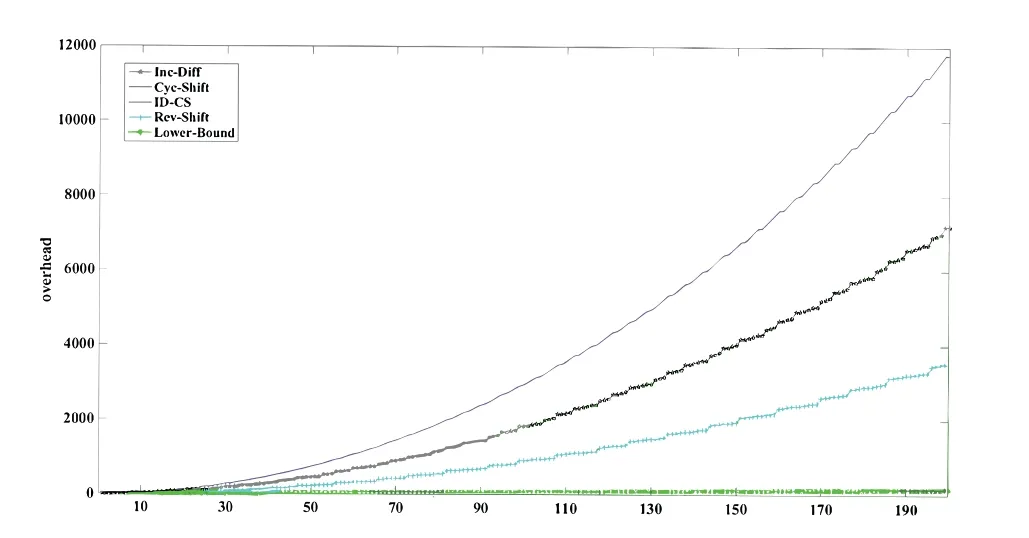
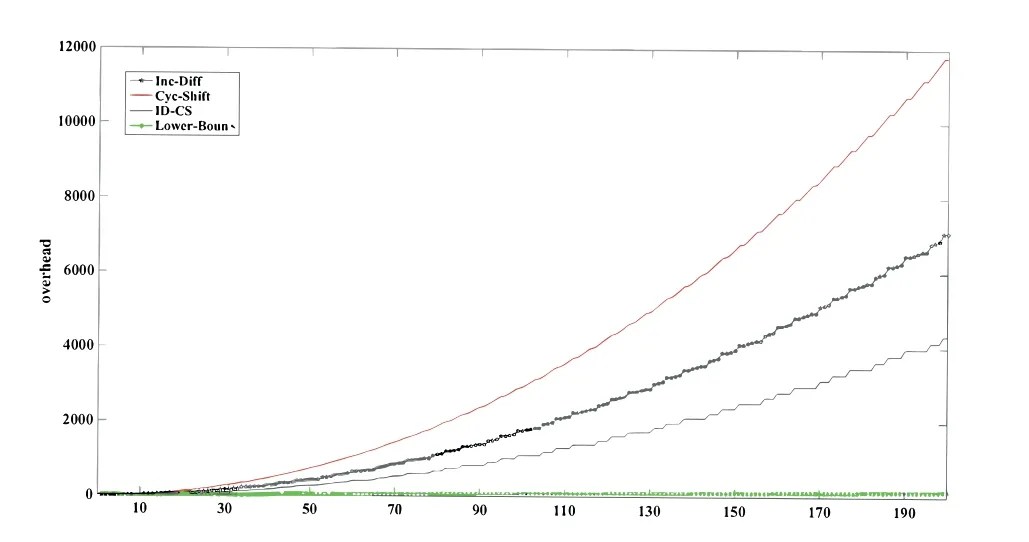
Abstract: To provide reliability in distributed systems,combination property (CP) is desired,where k original packets are encoded into n ≥k packets and arbitrary k are sufficient to reconstruct all the original packets.Shift-and-add (SA) encoding combined with zigzag decoding(ZD)obtains the CP-ZD,which is promising to reap low computational complexity in the encoding/decoding process of these systems.As densely coded modulation is difficult to achieve CP-ZD,research attentions are paid to sparse coded modulation.The drawback of existing sparse CP-ZD coded modulation lies in high overhead,especially in widely deployed setting m Keywords: distributed system;shift-and-add;zigzag decoding;sparse coded modulation The volume of data grows explosively in the era of big data[1,2],which exceeds the processing capability of a single computing node.For distributed implementation,certain nodes may be down or become stragglers[3].For example,in a data center on Facebook,more than 100 failures of stragglers may occur every day [4],which significantly slows down the completion time. Network code (NC) [5] tackles the straggler problem by cleverly introducing redundancy to provide combination property (CP) [6],[7]:koriginal packects are encoded inton≥kpackets,and anykout of thesenare able to recover the originalkpackets.Adopting NC to obtain CP has been widely adopted in distributed systems,including distributed communication network[8–10],distributed storage(DS)[11–13],coded distributed computing(CDC)[14–18],and distributed learning[19]. Prevalent coded modulation methods to obtain CP is the Reed-solomon (RS) [20],which needs to perform encoding and decoding operation over large finite field,and hence the complexity is high especially for the decoding process since it contains gaussian elimination [21].In addition,it has the problem of high power consumption [22],device overheats [23],etc.These drawbacks become prominent in applications where big data is frequently read and written[24]or deployed in devices with limited computing power and resources[25],[26],[27,28]. Therefore,low-complexity encoding and decoding is more desirable.An efficient method of reducing complexity is let shift-and-add(SA)operation replace linear combination in the encoding process,and backward substitution,say zigzag decoding(ZD)[29],replace the time-consuming gaussian elimination process.Combination of SA and ZD to obtain CP is called CP-ZD.As densely coded modulation is difficult to achieve CP-ZD [30],research attentions are paid to sparse coded modulation.Within sparse coded modulation,the work in[31]proposes the first CP-ZD coded modulation by designing the shift matrix (that characterizes the number of shifts when each component compose the encoded packets)based on increasing the shift difference according to Vandermonde matrix,and is named Inc-Diff.In order to reduce the overhead,by cyclically shifting one particular designed row to form the shift matrix,Cyc-Shift was constructed in [32].Later,a full parameter (n,k) CP-ZD coded modulation was constructed based on increasing difference(ID)and Cyclic Shift(CS),named ID-CS[33]. In summary,the overhead of existing CP-ZD coded modulation is high,especially for most common scenarios wheremis between 20% and 80% ofk[34],[35].In addition,as far as we know,there is no analytical bound that characterizes the overhead of CP-ZD coded modulation.In this work,we will address these two problems.In Sec.II,preliminaries are given.In Sec.III,code design for Rev-Shift is elaborated.In Sec.IV,a lower bound that characterizes the overhead is derived.Comparison of overheads is given in Sec.V.Finally,conclusions are drawn in Sec.VI. We first formulate system model,and then illustrate design objective and guidelines. Consider (n,k) CP-ZD systematic code where there firstksource packets serve as the fistkencoded packets,and the remainingm≜n-kencoded packets are obtained by appropriate SA operation over the firstksource packets.As illustrated in Sec.I,we consider to construct encoding method that can reduce the storage overhead in the scenario wherem The originalksource packets are represented bys1tosk,with length equal toLand thel-th element(may be a number for CDC environment [14],or a bit for storage systems [33]) ofsidenoted bysi,l,l∈{1,2,...,L}.Letc1tocndenote thenencoded packets.Due to systematic nature,we have systematic packetsci=sifor alli∈{1,2,···,k}≜K,and we call encoded packetck+jparity packet,i∈{1,2,···,m}≜M,j∈{1,2,...,m}. More specific expression for SA is that the source packet is first shifted to the right by a number of elements,and then addition operation is performed at the corresponding position,where the addition may either be in real field for CDC or in binary field for storage systems.ZD is simply a substitution process,namely eleminating the exposed elements.Detailed elaboration may refer to Example 1. Letm×kdimension matrixTrepresent the numbers of elements shifted by the source packets,withTijdenoting the number of elements that source packetsjshifted to the right when forming encoded packetck+i.We hence callTthe shift matrix.The maximum of all elements in the matrixTis called overheadOH. Example 1.RefertoinFigure1.TheSAencoding isdescribedindetailusingthecode(n,k)=(4,2).Therearek=2sourcepackets,s1,s2eachwith lengthL=5.Inencodedpackets,c1=s1,c2=s2,andc3,c4areobtainedbySAencodingwiththenumberofelements(s1,s2)shiftedtotherightby(0,1)and(0,2),respectively.Specifically,inordertoconstructc3,s1ands2areshiftedtotherightby0and 1elementrespectivelyandthenadded.Similarly,c4isobtainedbyshiftingthesourcepackageby0and2 elementsrespectivelyandthenadded.Inthiscase,the lengthofc3is6andthelengthofc4is7,andOH=2. Figure 1.ZD decoding process of(4,2)code. Supposec3,c4areutilizedtorecoverthesource packagess1,s2.RefertoFigure1,theorderofthedecodedinformationelementsisindicatedbythenumbersinparentheses.Firstofall,itcanbeseenfrom Figure1thats1,1ofc3ands1,1,s1,2ofc4areexposedelements,sos1,1ands1,2canberegardedas thefirstandseconddecodedpositionsrespectivelyand theirindicesaremarkedas1and2respectivelyinthe parentheses.s2,1canbedecodedbysubstitutings1,2intothesecondpositionofc3,whichisthethirdinformationelementtobedecoded,soitsindexismarked as3intheparentheses.Similarly,s1,3canbeobtainedbysubstitutings2,1intothethirdpositionofc4whoseindexcanbesetto4.Thisdecodingprocess continuesuntilalltheelementsofs1ands2arerecovered.DuringtheZDprocess,wecalltheresultants encodedpacketaftersubstitutionasdegeneratedencodedpacket. The objective is to design CP-ZD codes with smallOH(or maximal elment inT) in the scenario whenm Define shift difference forp∈M,i,j∈K.Theorem 1 from [32],as restated below,gives a necessary condition for a code to be CP-ZD. Theorem 1.ThecodedefinedbyshiftmatrixTisCPZDonlyifforallpq,i≠j,i,j∈Kandp,q∈M. We refer to this property as Distinct Shift Difference(DSD).The guideline to design Rev-Shift code is to first satisfy Theorem 1 and then make the overhead as small as possible.In addition,the derivation of overhead bound should also obey Theorem 1. We first design Rev-Shift code,and then prove that it possesses CP-ZD. To lower the storage overhead in the case ofm Firstly,we design a base matrixTBbased on value(n,k),which mimics existing code design.Secondly,we invert each row from the second row to obtain the inverse matrixTR.Thirdly,vertically concatenateTBandTRto form matrixTG.Lastly,fetch the firstmrows from matrixTGto form shift matrixT.Detailed processing is illustrated below: Step 1,Parameter determination:Letrdenote the number of rows inTB,withkdenoting the number of columns inTB.AsTRhas one row less thanTB,the number of rows inTBcan be determined as: Step 2,Construct base matrixTB:Let the first row ofTBbe[0,0,0,···,0].Starting from the second row,let the(i,j)-th element be(i-1)×(j-1),2≤i≤r,j∈K.More specifically,TBis Step 3,Construct inverted matrixTR:Except the first row ofTB,reverse the other rows ofTBto obtain(r-1)×kTRas Step 4,Determine shift matrixT:Vertically concatenateTBandTRto obtain a (2r-1)×kmatrix.Fetch the firstmrows ofTGto obtainT. Example 2.Suppose(n,k)=(13,7),wehavem=n-k=6.Therefore,thedimensionofshiftmatrixT is6×7.Accordingto(2),wehave BasematrixTBisthenconstructedtobe ReversematrixTRisthenobtainedtobe Finally,shiftmatrixTisobtainedtobe Before proving the CP-ZD property of the Rev-Shift code,we first give one lemma and two facts.Afterwards,we then use them in the proof. 3.2.1 Basic Lemma and Facts Lemma 1.Givenanyrowindicesi,jandcolumn indicesm,nofshiftmatrixTspecifiedbyRev-Shift code,wherei≠j,m≠n,wehave Proof.The proof of(a)can be obtained directly from the construction rules ofT,and (b) actually follows from the DSD property.Proof of (c) is divided into three cases: Case 1.Tim and Tjm are both from TB:Onone hand,since>0,wecandirectlyobtainTin>Tim.Ontheotherhand,ifTim>Tjm,wecandirectlyobtainthatTjmisaboveTim.Sincethedistancebetweenthesametwocolumnsindifferentrows increasesrowbyrow,wehaveissatisfied. Case 2.Tim and Tjm are both from TR:Since>0,wehaveTin>Tim,andfurtherdraw theconclusionthatTimistotherightofTininTR.In addition,asTim>Tjm,weobtainthatTjmisabove TiminTR.Wecanalsodirectlyobtain Case 3.Tim and Tjm do not simultaneously locate in TB or TR:Itisdividedinto2sub-cases: Sub-case2,TimcomesfromTR,Tjmcomesfrom TB:From>0,weknowthatTin>Tim,and henceTimistotherightofTininTR.Therefore,Tjm istotherightofTjninTB.Inaddition,asTim>Tjm,wehave=Tjn-Tjm<0.Therefore,> Fact1.Agraphthathasatleastasmanyedgesas verticesmustcontainacycle[36]. Fact2.The length of each encoded packet becomes shorter and shorter as the ZD decoding process proceeds.LetSidenote the index set of the source packets in the degenerated encoded packetck+i.The ZD decoding succeeds only when we can find one degenerated encoded packetck+iwhose associated|Si|=1. 3.2.2 Formal Proof of Possessing CP-ZD CP-ZD is equivalent to arbitrarykpackets from thenencoded packets can be recovered by the ZD algorithm. Theorem 2.Arbitrarykpacketsfromthenencoded packets,whoseshiftmatrixischaracterizedbyTof Rev-Shiftcode,canberecoveredbytheZDalgorithm.Proof.Assume that thekencoded packets are composed ofJ≤Kparity packets andk-Jsystematic packets.The systematic packets can be directly substituted into theJparity packets,which results inJdegenerated parity packets withJsource packets yet to be recovered.In other words,the number of undecoded original packets isJ. We useIto denote the index set ofJparity packets,while the index set ofJsource packets is denoted byJ⊂K,where |I|=|J|=J.In addition,the degenerated shift matrixT-(submatrix ofTby fetching corresponding rows and columns) corresponding to theJparity packets is a matrix of dimensionJ×J.Therefore,the decoding task can be reduced to recovering the remainingJsource packets from theJdegenerated parity packets by ZD algorithm.We use the contradiction method. Suppose the ZD algorithm enters a deadlock.This occurs only if |Si|≥2 for alli∈I.Remove arbitrary elements fromSiuntil |Si|=2 for alli∈I.Construct a graph ofJvertices,which are indexed byJ.There is an edge between verticesuandvif and only if bothuandvbelong toSifor somei∈I.By Lemma1b,these edges must be distinct,so there areJedges in total.By Fact 1,there must be a cycle in the graph. But Vasilissa saw how she snarled41 at her and she answered: The three questions are enough for me. As thou hast said, grandmother, I would not, through knowing over much, become too soon old. Letpbe the number of edges in such a cycle.As mentioned above,by Lemma1b,the constructed graph is a simple graph,which has no cycle of length two.Therefore,p≠2 and hence 3≤p≤J.Furthermore,let thepedges be (d1,d2),(d2,d3),...,(dp-1,dp),(dp,d1).Recall that when constructing the graph,each edge is defined via one of the parity packets.Letr1,r2,...,rp∈Ibe the indices of the parity packets associated with thepedges,respectively.Define For notational simplicity,we definedi≜dimodp.Note that the existence of the edge (di,di+1),associated with parity packetck+ri,indicates that the number of elements that have been decoded fromSdiminus the number of elements that have been decoded fromis given by.By(9),we must have for otherwise the number of decoded elements of thepsource packets would not be consistent.The situation can be discussed in two cases. Case 4.The shift matrix associated with the deadlock does not contain the first row,namely the all 0 row:ByLemma1a,allthetermsintherighthandside of(9)arenon-zero.Furthermore,dueto(10),these termscannotallhavethesamesign.Therefore,we mustbeabletofindavalueofi∈{1,2,...,p}such that and where the above two inequalities follow from (11)and(12),respectively.Since it suffices to consider only the case where By(12),(13),and Lemma1c,we have Re-labeling the edges is equivalent to changing the direction of the loop.Since in fact the direction of the loop is not specified,either direction is ok,and hence(18)is equivalent to(14).In a similar manner,(14) and (18) can be obtained whenandsimultaneously locate inTR. Case 5.The shift matrix associated with the deadlock contains the first row,namely the all 0 row:When∆loopcontainsashiftdifferencevalue0,the numberofrowsinthecodingmatrixthatconstitutethedeadlockmustbegreaterthan2,namely,thenumber ofitemsontherighthandsideof(9)mustbegreater than2.Thereasonisasfollows:Supposethenumber ofitemsisexactly2,thereisanall-0rowandanarbitraryrowwithashiftdifferencevaluenotequalto0.Inotherwords,therewillbeonlyonevalueequalto0,andtheotherelementswillnotbeequalto0,sothat∆loop≠0,whichcontradictstothedeadlockfact. When the number of terms is greater than 2,to ensure ∆loop≠0,we can still find a benchmark valuerifromr1,r2,···,rpthat satisfies(11)and(12).Similar to the proof of Case 1,(14) or equivalentlycan be proved. Notice that the key idea that leads to the contradiction is that in the deadlock state,the numbers of elements decoded by two distinct parity packets are not the same,as illustrated in Figure 2,where the part with dashed lines indicate the elements of the original packets that have been decoded,and the part with solid lines indicates the elements yet to be decoded. Figure 2.A graphical illustration to show that(14)is impossible. Suppose at this deadlock,exactlyq≥0 elements ofsdi+1have been decoded.The existence of the edge(di,di+1)in our constructed graph indicates that there is no exposed element in parity packetand exactlyq+elements ofhave been decoded(Refer to the upper portion of Figure 2). To better understand the above proof,examples are given for Case 1(Example 3)and Case 2(Example 4),respectively. Example 3.FollowingExample2,considersetting(n,k)=(13,7).Assumethatencodedpackets c1,c5,c6,c7,c9,c11,c12aregiven,whichindicatesthat theencodedpacketcorrespondingtoall0rowisnot contained.Bysubstitutingsystematicpacketsinto paritypackatesc9,c11,c12,wetransformtheproblemintorecoveringtheremainingsystematicpackets s2,s3,s4fromdegeneratedpacketsc9,c11,c12through theZDalgorithm.Ifthedecodinghasfalleninto deadlock,wehave|S9|=|S11|=|S12|=2.Accordingtothegraphconstructionrule[36],thisis agraphwith3verticesandthenumberofedgesin thisloopisp=3.Drawthecorrespondinggraph inTasshowninFigure3(a).Letd1,d2,d3correspondtocolumn2,column3,andcolumn4,respectively.Letr3,r1,r2correspondtoparitypacket c9,c11,c12,respectively.Atthistime,theloopexists∆loop1=(6-3)+(3-4)+(1-3)=0with∆loop1representedasshowninFigure3(b),wherethereexistand=-2<0.Therefore,accordingto(14),δ==3-1=2>0issatisfied. Figure 3.Example of ∆loop1=0. ThedecodingsituationisillustratedinFigure4.SupposeL=12,andq=7elementsofs3inc11havebeenrecovered/decoded.Thefirstunknownelementofs3inc11iss3,8.From=3,wecan obtainthatthenumberofelementsdecodedins2is=7+3=10. Figure 4.∆loop1=0(deadlock)contradicts with the actual decoding situation. Inc9,sincethenumberofelementsdecodedbys2is 10and=1,wecanobtainthatthenumberof elementsdecodedins3isatleastq+=7+2=9,whichcontradictstheoriginalassumption thatq=7elementsofs3havebeendecoded.Therefore,thedeadlockdoesnotexist. Example 4.FollowingExample2,considersetting(n,k)=(13,7).Assumethatencodedpackets c1,c2,c6,c7,c8,c10,c13aregiven,whichindicatesthat theencodedpacketc8correspondingtotheall0row iscontained.Similarly,aftersubstitutingavailable systempacketss1,s2,s6,s7intotheparitypackets c8,c10,c13,weobtaintheequivalentsystemofrecoveringtheoriginalpacketss3,s4,s5fromdegenerated packetsc8,c10,c13. Supposedecodingcannotproceed,whichmeans thereexists|S8|=|S10|=|S13|=2.Accordingto previousproof,wecanconstructagraphwith3verticesandcorrespondingloopwithp=3edgesaswell.DetailsmayrefertothegraphinTasshowninFigure5.Letd1,d2,andd3beassociatedwithcolumns4,3,and5,respectively.Letr1,r2,andr3beassociated withparitypacketsc13,c8,andc10,respectively.There exists∆loop2=(8-6)+(0-0)+(6-8)=0asillustratedinFigure5,andthereexists=2>0and=-2 <0inthisloop.Therefore,according toequation(14),δ==2-(-2)=4>0issatisfied. Figure 5.Example of ∆loop2=0. ThedecodingsituationisasshowninFigure6.SupposethelengthofeachoriginalpacketisL=12,q=4elementsofs4inc13havebeendecoded,thefirstunknownelementofs4inc13iss4,5.Fact=2indicatesthatthenumberofelementsalreadydecodedins3isq+=4+2=6.Inc10,sincethenumberofelementsdecodedins3is6,and=-2,wecanobtainthatthenumberofelementsdecodedin s4isatleastq+=4+4=8.Thiscontradictstheoriginalassumptionofq=4elements,whichmeansthedeadlockdoesnotexist. Figure 6.∆loop2=0(deadlock)contradicts with the real decoding situation. In this section,based on the DSD property in Sec.II,we derive a lower bound on the overheads.Note that DSD is a necessary instead of sufficient condition for possessing CP-ZD,and hence the characterized bound based on DSD is a lower bound.We first give some lemmas and theorems. Lemma 2.Ifanm×kshiftmatrixTsatisfiesthe DSDproperty,itstransposeT′mustalsosatisfythe DSDproperty. Proof.Firstly,consider 2×2 matrix.Suppose matrixsatisfies DSD property,namelyab≠c-d.It is equivalent toa-c≠b-d,which indicates thatalso satisfies DSD property.We then consider general dimension of shift matrixT.For its arbitrary 2×2 submatrix,say indexed by rowsp,q∈{1,2,···,m}and columnsi,j∈{1,2,···,k},namely submatrixwe have.Previous paragraph indicates for,or equivalently,the submatrix ofT′indexed by rowsi,jand columnsp,q,we have.Therefore,T′satisfies DSD property. Lemma 3.ForashiftmatrixTwithmrowsandkcolumnsthatsatisfiestheDSDproperty,wehavem≤2OH+1. Proof.Firstly,consider caseOH=1,all elements inTbelong to set{0,1},and hence the corresponding shift difference belong to set{-1,0,1}.Therefore,in the ideal case,the maximum number of rows in the shift matrix that satisfies the DSD property is 3,namely,m≤3. Now consider caseOH=2,all the elements inTbelong to set{0,1,2}.The corresponding shift difference belong to set{-2,-1,0,1,2}.Therefore,the maximum number of rows in the shift matrix that satisfies the DSD property is 5,namely,m≤5. Now consider general value ofOH,all the elements inTbelong to set{0,1,2,...,OH}.The corresponding shift differences belong to set{-OH,-OH+1,...,-1,0,1,...,OH-1,OH}.Therefore,we obtainm≤2OH+1. According to Lemma 3,the relationship between the overheadOHand the number of rowsmbecomes,which is listed in Table 1.The following theorem can be inferred from Lemma 3. Table 1.Relationship between the number of rows m and overhead OH. Theorem 3.ForshiftmatrixTwithmrowsandk columnsthatsatisfiestheDSDproperty,giventhe overheadOH,wehavem≤2OH+1andk≤2OH+1. Proof.Given overheadOHassociated with shift matrixT,Table 1 gives constraint onm≤2OH+1.We also claim thatk≤m,which is proved in the following.According to Theorem 2,its transposeT′alsosatisfies the DSD property.In this case,the dimension ofT′isk×m,which must also satisfym≤k,namelyk≤2OH+1. Therefore,we obtain a lower bound on the overhead: We find that this bound is tight,namely it overlaps the overehead of existing CP-ZD codes,in certain cases as shown in the following example: Example 5.Firstly,considercaseOHLBD=1.We canfindaCP-ZDcodewithm=k=3whoseoverheadexactlyequalsOHLBD=1.Todothat,wefirstconstructTB=andthenconstructTG=.Itcanbeverifiedbyexhaustivesearchthatany3×3submatrixTfromTGsatisfies CP-ZD. Secondly,considercaseOHLBD=2.Wecanfind severalCP-ZDcodeswithm=5,k=4orm=4,k=5whoseoverheadexactlyequalsOHLBD=2.DetailedTarelistedas: Note that to our best knowledge,we are the first that found tight bound for CP-ZD code in certain scenarios. In this section,we compare the overhead among existing CP-ZD codes (including Inc-Diff [31],Cyc-Shift[32],ID-CS codes[33]),our proposed Rev-Shift and lower bound as characterized in (19),whose expressions are listed below: We execute comparisons on two settings,one is fixingkand varying,and the other is fixingαand varyingk. We focus on the scenario wherem The overheads fork=50 andk=100 are plotted in Figure 7 and Figure 8,respectively.It can be observed that the advantage of Rev-Shift over existing codes is significant.However,the lower bound is tight only whenαapproaches 0 or equivalently whenmapproaches 0. Figure 7.Comparison of the overhead at k=50. Figure 8.Comparison of the overhead at k=100. We fixαand varynfrom 10 to 200.In particular,by fixingα=0.3,1,and 3,respectively,we plot Figure 9 and Figure 10,where Rev-Shift code only occurs in the case whenm Figure 9.Comparison of the overhead,m Figure 10.Comparison of the overhead,m ≥k. For frequently used scenariom The research was jointly supported by research grants from Natural Science Foundation of China(62071304),Guangdong Basic and Applied Basic Research Foundation (2020A1515010381,2022A1515011219,20220809155455002),Basic Research foundation of Shenzhen City(20200826152915001,20190808120415286),and Natural Science Foundation of Shenzhen University (00002501),Xinjiang Uygur Autonomous Region Natural Science Foundation General Project(2023D01A60).I.INTRODUCTION
II.PRELIMINARIES
2.1 System Model
2.2 Design Objective and Guideline
III.REV-SHIFT CODE DESIGH FOR m
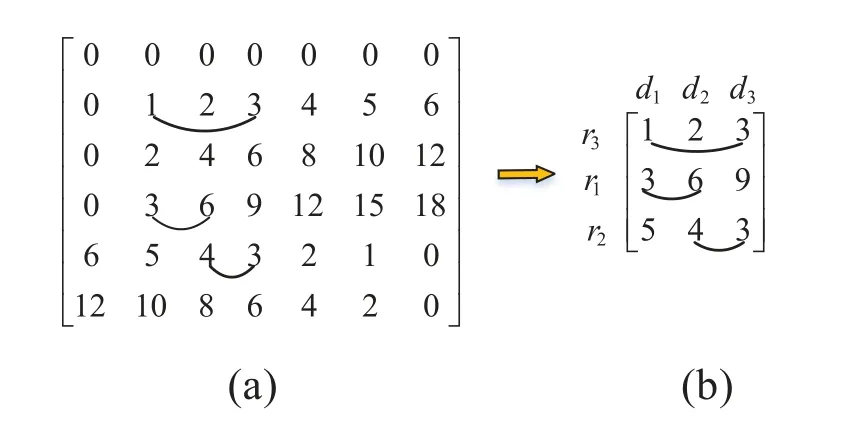
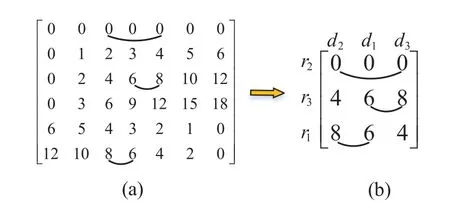
3.1 Design of Rev-Shift Code
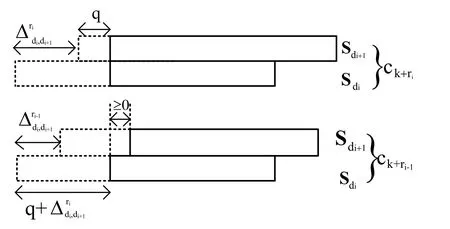
3.2 Proof that Rev-Shift Possesses CP-ZD

IV.LOWER BOUND ON THE OVERHEAD
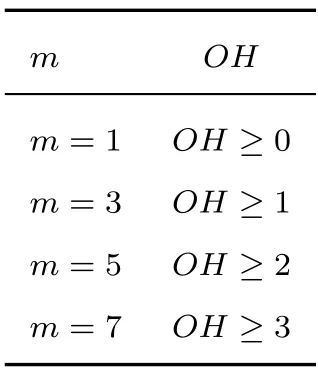
V.COMPARE OF OVERHEADS
5.1 Setting 1,Fix k and Vary α:
5.2 Setting 2,Fix α and Vary k:
VI.CONCLUSION
ACKNOWLEDGEMENT

