UAMP-Based Delay-Doppler Channel Estimation for OTFS Systems

Zhongjie Li ,Weijie Yuan,* ,Qinghua Guo ,Nan Wu ,Ji Zhang

1 Department of Electronic and Electrical Engineering,Southern University of Science and Techonology,Shenzhen 518055,China

2 School of Electrical,Computer and Telecommunications Engineering,University of Wollongong,Wollongong,NSW 2522,Australia

3 School of Integrated Circuits and Electronics,Beijing Institute of Technology,Beijing 100081,China

4 School of Mathematics and Statistics,Henan University of Science and Technology,Luoyang 471000,China

*The corresponding author,email: yuanwj@sustech.edu.cn

Abstract: Orthogonal time frequency space (OTFS)technique,which modulates data symbols in the delay-Doppler(DD)domain,presents a potential solution for supporting reliable information transmission in highmobility vehicular networks.In this paper,we study the issues of DD channel estimation for OTFS in the presence of fractional Doppler.We first propose a channel estimation algorithm with both low complexity and high accuracy based on the unitary approximate message passing (UAMP),which exploits the structured sparsity of the effective DD domain channel using hidden Markov model (HMM).The empirical state evolution (SE) analysis is then leveraged to predict the performance of our proposed algorithm.To refine the hyperparameters in the proposed algorithm,we derive the update criterion for the hyperparameters through the expectation-maximization(EM)algorithm.Finally,Our simulation results demonstrate that our proposed algorithm can achieve a significant gain over various baseline schemes.

Keywords: orthogonal time frequency space(OTFS);channel estimation;hidden Markov model (HMM);unitary approximate message passing(UAMP)

I.INTRODUCTION

In the realm of wireless communication,future networks are envisioned to provide reliable and efficient communication in high-mobility scenarios,including Enhanced Mobile Broadband (eMBB),Internet of Things (IoT),vehicle-to-vehicle communication (V2V),high speed train (HST),and millimeter wave (mm-Wave) communication.However,the widespread use of orthogonal frequency division multiplexing (OFDM) modulation in current mobile networks may face significant challenges in these highmobility scenarios.The high Doppler spread of such scenarios can result in inter-carrier interference(ICI),which significantly deteriorates the performance of OFDM.As a result,it becomes challenging to apply OFDM to future communication systems without proper mitigation techniques.

Recently,the authors in [1] introduced a new communication paradigm named orthogonal time frequency space(OTFS)modulation.OTFS multiplexes symbols in the delay-Doppler (DD) domain rather than the classic time-frequency(TF)domain[2].Relying on the DD domain signal representation,OTFS provides a waveform optimally coupling with the wireless channel,which results in improved robustness against dynamic environments due to the delayresilience and Doppler-resilience properties.Futhermore,the DD representation of the wireless channel exhibits desirable features,such as separability,stability,compactness,and possible sparsity,making channel estimation and data detection easier and more efficient[3].

Accurate channel estimation is essential to obtain the channel state information(CSI)for reliable detection.In OTFS,the channel information,i.e.the delay shifts and Doppler shifts are discreted at the DD grids.The delay resolution and Doppler resolution depend on the bandwidth and time duration,respectively.In practical scenarios,bandwidth is often sufficient to provide adequate delay resolution,while time duration may be limited due to the low latency requirement in future communication.In such cases,fractional Doppler must be taken into consideration.For integer Doppler,the effective channel in DD domain is sparse.However,in the fractional Doppler case,the effective DD channel is spread across all the Doppler indices,which reduces its sparsity and negatively impact channel estimation performance[4].To overcome this challenge,developing an efficient channel estimation algorithm for the fractional Doppler case is critical.

Substantial research efforts have been devoted to design channel estimation methods for OTFS in the presence of fractional Doppler [5–12].In [5],a pilot pattern was proposed that involves embedding a single pilot in DD domain and inserting either a full guard space along the Doppler domain or a reduced guard space between the pilot symbols and data symbols to suppress inter-Doppler-interference(IDI).Subsequently,a threshold-based estimator was adopted to recover the effective DD domain channel.However,the threshold-based estimator lacks performance,especially in the low signal-to-noise ratio(SNR)regions.To address this issue,some compressive sensing-based methods were proposed to capturing the channel sparsity by leveraging sparsity structure of the effective DD domain channel.The authors in [6] presented a three dimensional structured orthogonal matching pursuit (3D-SOMP) algorithm that exploits normal sparsity along the delay domain,block-sparse along the Dopppler domain,and burst-sparse along the angle domain.Despite its effectiveness,the channel estimation performance for the 3D-SOMP algorithm declines when the number of channel paths is not perfectly known.In [7],a novel pilot pattern was proposed that eliminates the need for a guard space between pilot and data symbols.A sparse Bayesian learning (SBL)-based channel estimation algorithm was then presented to solve the formulated sparse recovery problem.The method proposed in [10] extended the algorithm in [7] by using block SBL algorithm with block reorganization(BSBL-BR).However,these two methods are computationally inefficient,especially for large OTFS frame sizes,due to the high complexity of the SBL algorithm.A novel off-grid channel estimation scheme was proposed in[9]to estimate the original DD domain channel response.This scheme was formulated as a 1D and 2D off-grid sparse recovery problem,and a SBL-based algorithm was presented as a solution to these problems.The proposed scheme differs from previous works in that it focuses on estimating the original channel response rather than the effective DD domain channel response.The estimation performance of this method,however,depends on the accuracy of the Taylor expansion in approximating the true dictionary.In summary,traditional algorithms are either unsatisfactory in terms of complexity or accuracy.Therefore,there is a pressing need for the development of efficient channel estimation algorithms in the presence of fractional Doppler.

In this work,we focus on addressing the issues of channel estimation for OTFS systems in the presence of fractional Doppler and propose an estimator with both high accuracy and low complexity.To put it crudely,the main idea of our work is to exploit the special channel sparsity structure caused by the frational Doppler and resort the Bayesian inference to recover the channel coefficients.The main contributions of our work are elaborated as follows:

• We demonstrate that the DD domain effective channel vector has characteristics of block sparsity or potential burst sparsity.To best explore the structured sparsity of the effective channel,a hidden Markov model (HMM) is employed to model the structured DD domain channel.The HMM prior has the following two advantages: i)This model does not assume the elements in channel vector are i.i.d.Instead,the HMM prior can characterize the support correlation between elements in the channel vector,ii) This model does not need the knowledge of the structure of the block,i.e.the size and the position of the block[13],thus possessing a higher flexibility to capture the structured sparsity of the channel vector compared with the prior model used in BSBL.These two merits render HMM prior suitable for characterizing the structured sparsity of the OTFS DD domain effective channel.

• The HMM prior is then incorporated with unitary approximate message passing(UAMP)algorithm to solve the formulated structured sparse recovery problem.With a factor graph representation of the formulated problem,a UAMP-HMM algorithm is proposed to efficiently solve the problem.UAMP[14] is a variant of AMP algorithm which has been widely used in compressive sensing field due to its low complexity and high robustness.UAMP inherits the advantages of AMP algorithm and extends AMP to handle a general system transfer matrix.These merits of HMM model and UAMP allows our proposed algorithm efficient to solve the OTFS channel estimation problem in the presense of fractional Doppler.

• We derive update expressions based on expectation-maximization (EM) [15] algorithm for automatically tuning the hyperparameters of the UAMP-HMM algorithm.The state evolution(SE) is also derived to accurately predict the performance of the proposed algorithm.We shows by simulations that,UAMP-HMM can approach the support-oracle bound closely,which demonstrate the effectiveness of our proposed algorithm.

The rest of paper is organized as follows.In Section II,we describe the OTFS model.In Section III,we formulate the channel estimation as a structured sparse signal recovery problem and present a channel prior based on HMM.In Section IV,we incorporate the HMM prior with UAMP algorithm to solve the formulated structured sparse recovery problem and provide the SE and EM updates for our proposed algorithm.Simulation results and performance analysis are given in Section V,followed by a conclusion in Section VI.

Notations: Boldface capital letters stand for matrices and lower-case letters stand for column vectors.The transpose is denoted by(·)T.We useN(x|µ,τ)to denote the Guassian distribution ofxwith meanµand varianceτ,and useBer(x|λ)to denote the Bernoulli distribution ofxwith parameterλ.The notationδdenotes impulse function.We use | · |·2to denote the element-wise magnitude squared operation.The notationMA→Bdenotes a message passing from nodeAto nodeBand useb(x)to denote the belief ofx.The Big O notation is denoted byO.

II.OTFS MODEL

In this section,we provide an overview of the fundamental OTFS transceiver,as depicted in Figure 1.At the transmitter side,the input sequence of bits is initially mapped onto a two dimensional DD grid of sizeN×M,whereNandMcorrespond to the numbers of the Doppler and delay indices,respectively.The DD symbols{x[k,l]∈A={α1,···,αA},k=0,···,N-1,l=0,···,M-1}are then transformed to TF domain using inverse symplectic fast Fourier transform(ISFFT),i.e.,

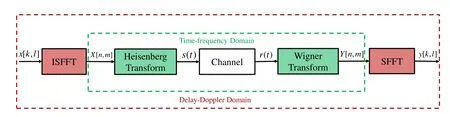
Figure 1.OTFS system model.

Next,the transformation to a continuous-time waveforms(t)is achieved via the application of the Heisenberg transform,utilizing a transmit filtergtx(t).In mathematical terms,this process can be represented as follows:

After the transmission of the signals(t)over a timevarying channel with delay-Doppler responseh(τ,ν),the resulting received signal in the time domain can be represented as,

where the channel response in DD domain can be succinctly expressed as,

whereδ(·)is the Dirac delta function,Pis the number of resolvable path,hi,τi,νidenote the channel coefficient,delay and Doppler shift associated with thei-th path,respectively.The delay and Doppler-shift taps for theith path are given by

wherelτiandkνicorrespond to the delay index and Doppler index of thei-th path,respectively;κνi,is a value in the range of,represents the fractional Doppler associated with theith path;M∆fis the total bandwidth of the system andNTis the duration of an OTFS block.

At the receiver end,the transformation of the received signalr(t)to the time-frequency(TF)domain is performed by utilizing a receive filtergrx(t),i.e.,

The signal undergoes a sampling process by means of a matched filter,thereby allowing us to obtain

Finally,Y[n,m]is transformed to DD domain symbolsY[k,l]using SFFT,i.e.,

If the transmit pulsegtx(t)and receive pulsegrx(t)satisfy the bi-othogonal property[1],i.e.

the input-output relationship in DD domain is formulated as,

where

Supposing that there exists only one path with delay index equal tolτi,the DD domain channel response atl=lτican be expressed as,

Noting that for the case of integer Doppler,i.e.=0,the above expression is simplified to

We can observe thathw[k,lτi] only has response atk=kνi.

For the case of fractional Doppler,i.e.κνi≠0,the magnitude ofhw[k,lτi]is given by

It can be observed from the above expression thathas values at all Doppler indiceskand reaches the peak value atk=.It is noting that the extent of expansion depends on the absolute value of.This spreading behavior renders the effective channel having the characteristics of block sparsity and potential burst sparsity,as illustrated in Figure 2.Based on this fact,we present a channel prior model which captures the characteristic of structured sparsity based on the HMM in the next section.

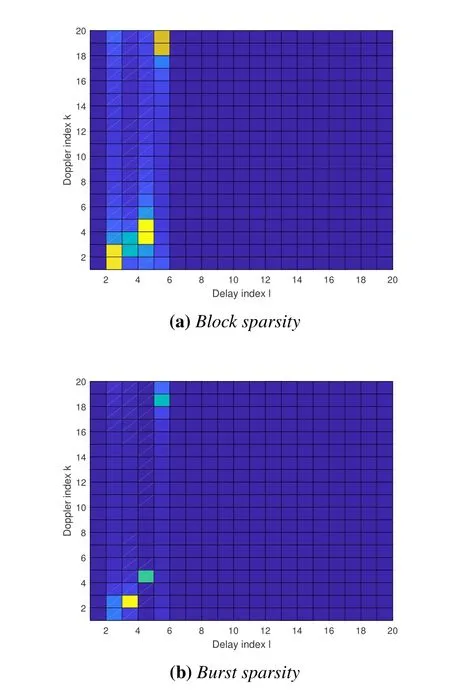
Figure 2.Illustration of effective channel matrix with block sparsity and burst sparsity. Block sparsity occurs when there is significant diffusion along all paths,while burst sparsity arises when there is non-uniform diffusion along the paths,with some of paths having minimal diffusion. It is noting that burst sparsity is more commonly observed in most scenarios.

III.PROBLEM FORMULATION AND STRUCTURED CHANNEL SPARSITY MODEL

3.1 Problem Formulation

In this study,we adopt the pilot pattern described in[11].This approach utilizes pilot symbols of dimensionsmp×np,which are embedded in the DD domain.To mitigate interference,a guard space is inserted between the pilot symbols and the data symbols.It is noteworthy that the use of multiple pilots can significantly decrease the PAPR,albeit at the cost of a minor reduction in spectrum efficiency [11].The received signal in the DD domain corresponding to the pilotsymbols is expressed as,

where the notationskmaxandlmaxrefer to the maximum indices of the delay taps and Doppler taps,respectively.The notation≪Nis an integer used for approximating the spreading caused by fractional Doppler.The effective channelhw[k′,l′] can be expressed as

As per (15),the expression can be reformulated in the form of a matrix-vector multiplication,represented as follows:

where r,v∈CT×1,T=(mp+lmax)(np+2kmax+2 ˆN).The term X∈CT×Jis constructed based on the pilot symbols,whereJ=(lmax+1)(2kmax++1).The vector representation,h,in the complex domain CJ×1,is derived from hwand exhibits burst sparsity characteristics,wherein its non-zero elements are concentrated in distinct clusters.To effectively utilize this burst sparsity of the h vector,a channel prior model based on HMM is proposed in the subsequent subsection.

3.2 Structured Sparsity Model for the Channel Based on HMM Prior

To characterize the burst sparsity of h,we employ the Bernoulli-Gaussian prior,i.e.,

where s=[s1,···sJ]Trepresents a stationary firstorder Markov process defined by two transition probabilities:p01≜p{sj=1|sj-1=0}andp10≜p{sj=0|sj-1=1}.It is noteworthy that the Markov parametersp01andp10are crucial in determining the average cluster size and the average gap between two clusters in h,respectively.In the steady state,the sparse rate is derived as,λ≜p(sj=1)=.Thus,p(sj=0)==1-λ.

The distribution of s is thus given by

with the transition probability

The initial distribution,denoted asp(s1),is established as the steady state distribution of the Markov chain,withp(s1=1)equal toλ.

IV.CHANNEL ESTIMATION ALGORITHM BASED ON UAMP

In this section,our goal is to utilize the HMM prior for inferring the effective channel coefficients and the noise precision parameterβfrom the received signal y.From a statistical inference viewpoint,this objective can be achieved by determining theaposterioridistributions of the corresponding variables.To attain this,we combine the HMM prior with the UAMP algorithm based on the factor graph representation.This combination enables us to compute the approximate posterior distributions (or beliefs) of the unknown variables h andβin an efficient manner.

4.1 Unitary Approximate Message Passing

The AMP algorithm is widely recognized to suffer from divergences in instances of a generic measurement matrix.However,the robustness of the AMP algorithm can be significantly enhanced through the application of a unitary transformation,as described in equation(17),i.e.,

where X=UΛV,Φ=ΛV,and w=UHv.The UAMP algorithm is summarized in Algorithm 1.

In UAMP,the function forms of the prior distributionp(h)determine the scalar functiongh(q,τq),thej-th element of which is given by

4.2 The Proposed UAMP-HMM Algorithm

In order to enable the integration of UAMP with HMM prior,we introduce the variable z=Φh.The factorization of the joint conditional distribution of the unknown variables is given by

where[Φ]trepresents thet-th row of Φ.Detailed information on the factors and distributions are available in Table 1.

Table 1.Factors and distributions.

In Figure 3,we present a factor graph representation for the factorization in equation(23).We partition the factor graph into three sub-graphs: Sub I,Sub II,and Sub III.It is important to acknowledge that the factor graph in Figure 3 contains loops,leading to the potential for belief propagation (BP) to produce incorrect posteriors.To overcome this challenge,we employ the“turbo”approach,as proposed in[16],for facilitating message passing between Sub II and Sub III.Specifically,this approach involves alternating between BP in Sub II and BP in Sub III,with the likelihood onsjderived from BP in one part serving as priors for BP in the other part.The most computationally intensive part,Sub II,can be calculated efficiently and with high robustness using UAMP.This leaves us with the task of focusing on the derivations of BP messages in Sub I and Sub III.

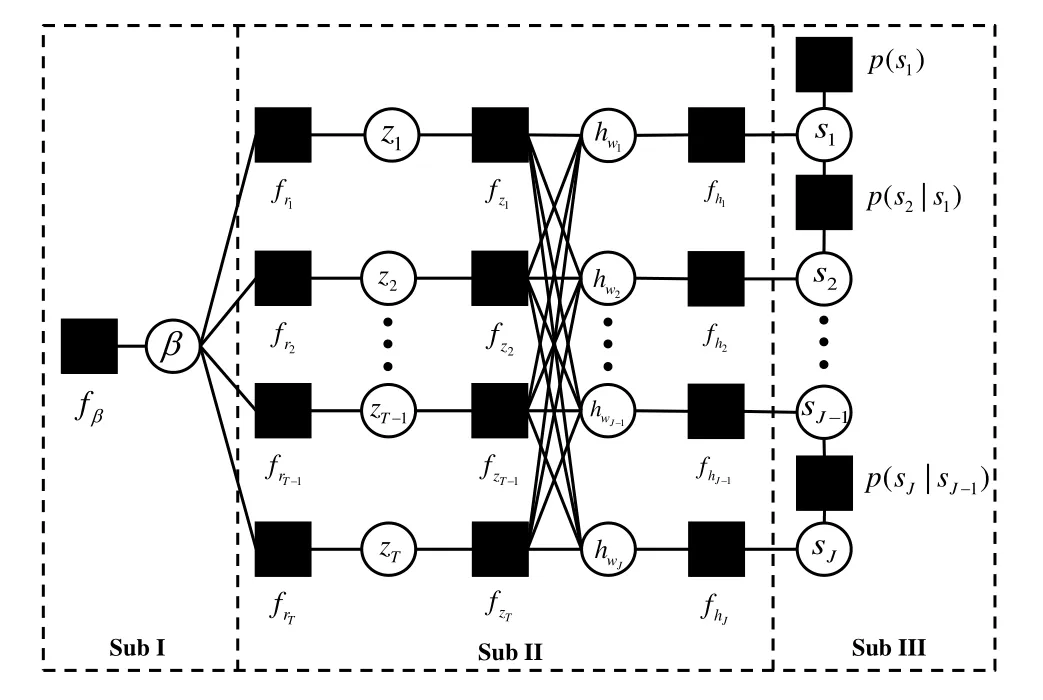
Figure 3.Factor graph of the joint distribution in(23).

4.2.1 Message Passing in Sub I

In accordance with the mean field rule[17],the message from factor nodeto variable nodeβcan be succinctly represented as

As shown in[18],the belief ofztis a Guassian formwith

Then the belief ofβis given by

4.2.2 Message Passing in Sub III

According the derivation of (U)AMP,the message from the variable nodehjto the factor nodefhjis expressed as

The message from the factor nodefhjto the variable nodesjis then calculated as

where

Subsequently,a forward-backward message passing algorithm,as described in [19],is executed over the Markov chain.The parameters for the forward and backward message passing are initialized according to the following specifications,

For the forward message passing,applying sumproduct rules to the message from factor nodep(sj|sj-1)to variable nodesjyields,

where the message from variable notesj-1to factor nodep(sj|sj-1)is calculated as

Substituding the above expression into eq.(34) results in:

where

Due to symmetry property,the backward messages can be updated using a similar way,i.e.

wherep0=p00+p10andp1=p11+p01.The message from the variable nodesjto the factor nodeis

where

Thus,the message from the factor nodeto variable nodehjis calculated as

The belief ofhjis then given by

where

and

So the minimum mean square error(MMSE)estimate ofhjcan be calculated as

The conditional variance can be calculated as

In conclusion,the UAMP-HMM is presented in Algorithm 2.As compared to the original UAMP algorithm,the UAMP-HMM algorithm incorporate a calculation of the MMSE estimate of the noise precision,β,from lines 4 to line 6,as well as the mean and variance of the posterior of the channel vector,h,from Lines 11 to 13.

4.3 Performance Analysis Based on State Evolution

In this part,we leverage the empirical state evolution to predict the performance of UAMP-HMM.In line 10 of Algorithm 2,the equivalent observation at thet′-th iterationcan be perceived as a noise-corrupted form of the actual channel coefficienthj.hj,i.e.,

whereεt′denotes the average MSE of{hj}after denoising in thet′-th iteration.The MSE in thet′+1-th iteration,is given by

4.4 Hyperparameters Learning Based on EM

In practice,the statistical parametersρ≜{p10,λ,ψh}can be learned by the expectation-maximization(EM)algorithm [20].Note that learning for three hyperparameters requires the knowledge ofp(sj|r),p(sj-1,sj|r) (which can be obtain from Appendix),andp(hj|r)(which is already calculated in Algorithm 2).The EM update scheme is shown in Figure 4 and the update criterion is shown in Algorithm 3.The details of derivation are available in the Appendix.

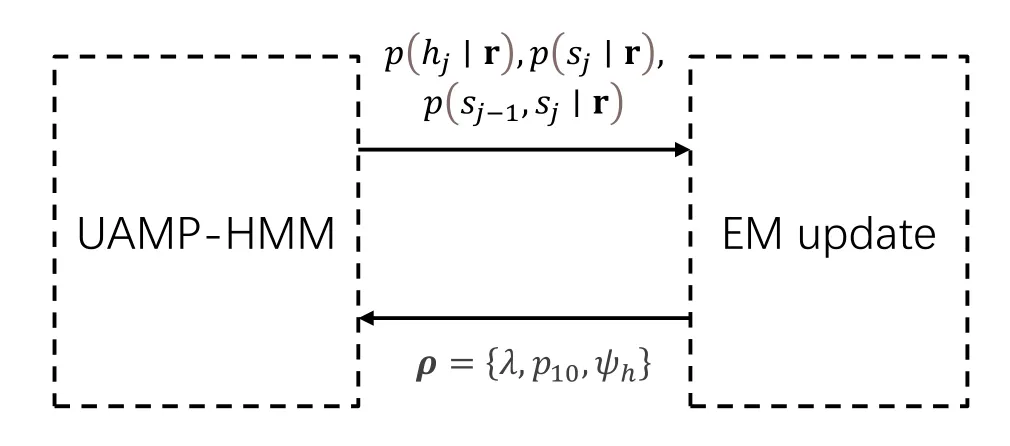
Figure 4.EM update for hyperparameters.

V.SIMULATIONS AND RESULTS

In this section,the performance of the proposed UAMP-HMM algorithm is evaluated and compared with various baseline algorithm i.e.threshold-based estimator [5],OMP [6],SBL [7],and UAMP-SBL[18]under fractional Doppler OTFS DD domain channel.The simulation parameters are specified as follows.An OTFS frame with 32 time slots and 128 subcarriers in the TF domain,i.e.M=128 andN=32,is considered.The carrier frequency is set as 3 GHz and the subcarrier spacing is set as 7.5 kHz.The total number of path is set asP=5,with a normalized maximum Doppler shift ofkmax=4 and a normalized maximum delay shift oflmax=10.The Doppler shifts are randomly generated within [-νmax,νmax]and delay shifts within [1,τmax] (excluding the first path withli=0).The channel gain is generated according a normal distribution with mean 0 and variance.In this study,normalization of data symbols is performed by ensuring thatE{|x[k,l]|}2=1.Our simulation utilizes 10 pilot symbols.Finally,quadrature phase shift keying(QPSK)modulation is used for the bit mapping.

In our simulations,the performance of the proposed UAMP-HMM algorithm is evaluated using the normalized mean square error (NMSE) and the bit error rate (BER).The NMSE is defined as NMSE=.As depicted in Figure 5,the NMSE performance of the proposed UAMP-HMM algorithm is compared to that of three conventional algorithms(i.e.threshold-based estimator[5],OMP[6],and SBL[7]) in a SNR range of 0dB to 30dB.To guarantee impartiality in comparison with the threshold-based estimator proposed in [5],we set the total power of the pilot symbols to be equal for the two pilot patterns.The power ratio between each pilot and data symbols in the adopted pilot pattern is calculated asSNRp==30 dB.For the single pilot pattern,the power ratio is 40 dB.The UAMPHMM algorithm,as presented in our results,demonstrates the lowest NMSE with a significant gain of 3dB over UAMP-SBL,5dB over OMP and SBL,and 13dB over the threshold-based estimator.This superiority is attributed to UAMP-HMM’s capability of exploiting the burst sparsity of the effective DD domain channel with fractional Doppler.

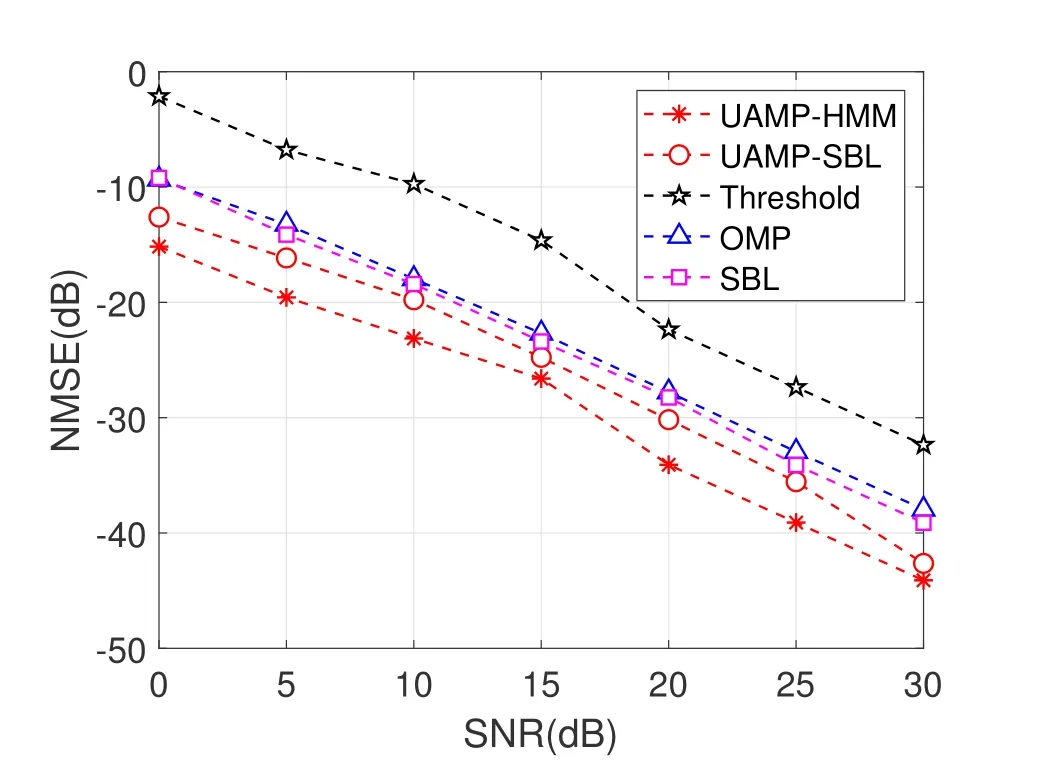
Figure 5.NMSE performance comparison.

In Figure 6,the BER performance of the OTFS system is compared with message passing-based detection algorithm proposed in [21] over SNR rang-ing from 0 dB to 10 dB.Furthermore,Figure 5 includes the BER performance of the OTFS system with a perfect channel as a reference.The results reveal that the performance of the OTFS system with our proposed channel estimation algorithm exhibits closer alignment with the performance of the perfect channel matrix,in comparison to other algorithms.

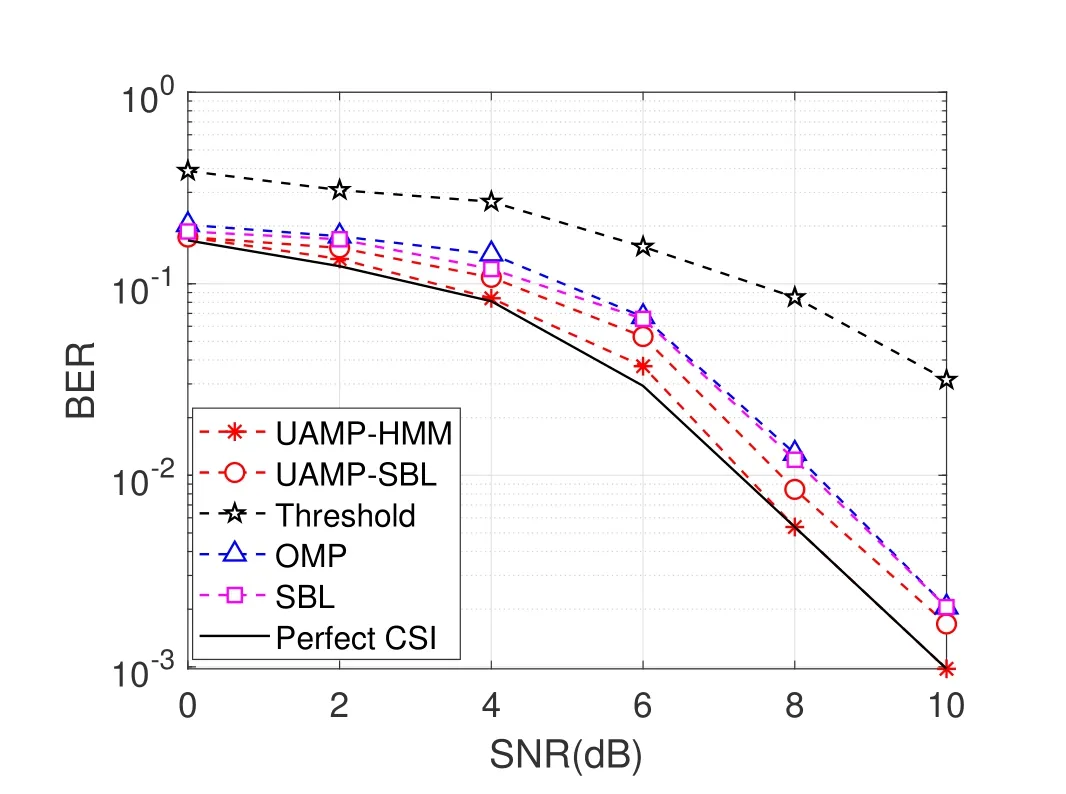
Figure 6.BER performance comparison.

The complexity of our proposed UAMP-HMM algorithm,OMP algorithm,and SBL algorithm is compared in Table 2,whereIrepresents the number of iterations and Num.iter represents the average number of iterations.It is worth noting that UAMP-HMM and UAMP-SBL involves an singular value decomposition(SVD),but it only needs to be computed once and may be carried out off-line.Thus we do not count this part into the computational complexity.The complexity of UAMP-HMM algorithm,is domained by two matrixvector product operations in Line 3 and Line 10 of Algorithm 2,i.e.O(TJ).It should be considered that the computational intricacy of the OMP algorithm rises with each iteration.In the case of no interference between paths,the number of nonzero elements in effective channel with fractional Doppler isP(2 ˆN+1),which leads to significantly increased number of iterations and thus high computational complexity for the OMP algorithm.The table shows that our proposed algorithm significantly reduces the computational overhead for channel estimation compared with OMP and SBL algorithms,in terms of less number of iterations and lower complexity per iteration.

Table 2.Complexity comparison.

Finally,we examine the SE performance of UAMPHMM algorithm.Figure 7 compares the NMSE performance of UAMP-HMM algorithm and UAMP-SBL algorithm [18] with SNR=15 dB and SNR=20 dB.It is noted that UAMP-SBL does not exploit the burst sparsity of the OTFS channels,so the comparisons with UAMP-SBL can be used to demonstrate the gain achieved by UAMP-HMM due to exploiting the burst sparsity.It can be observed from the results that the predicted performance matches well with the simulated performance.In addition,UAMP-HMM approaches the support-oracle bound closely,which demonstrates the effectiveness of our proposed algorithm.Moreover,in contrast with UAMP-SBL algorithm,UAMP-HMM converges faster and achieves a lower NMSE,which reveals that the HMM prior is better to capture the structured sparsity in the effective DD domain channel than the hierachy prior in SBL.

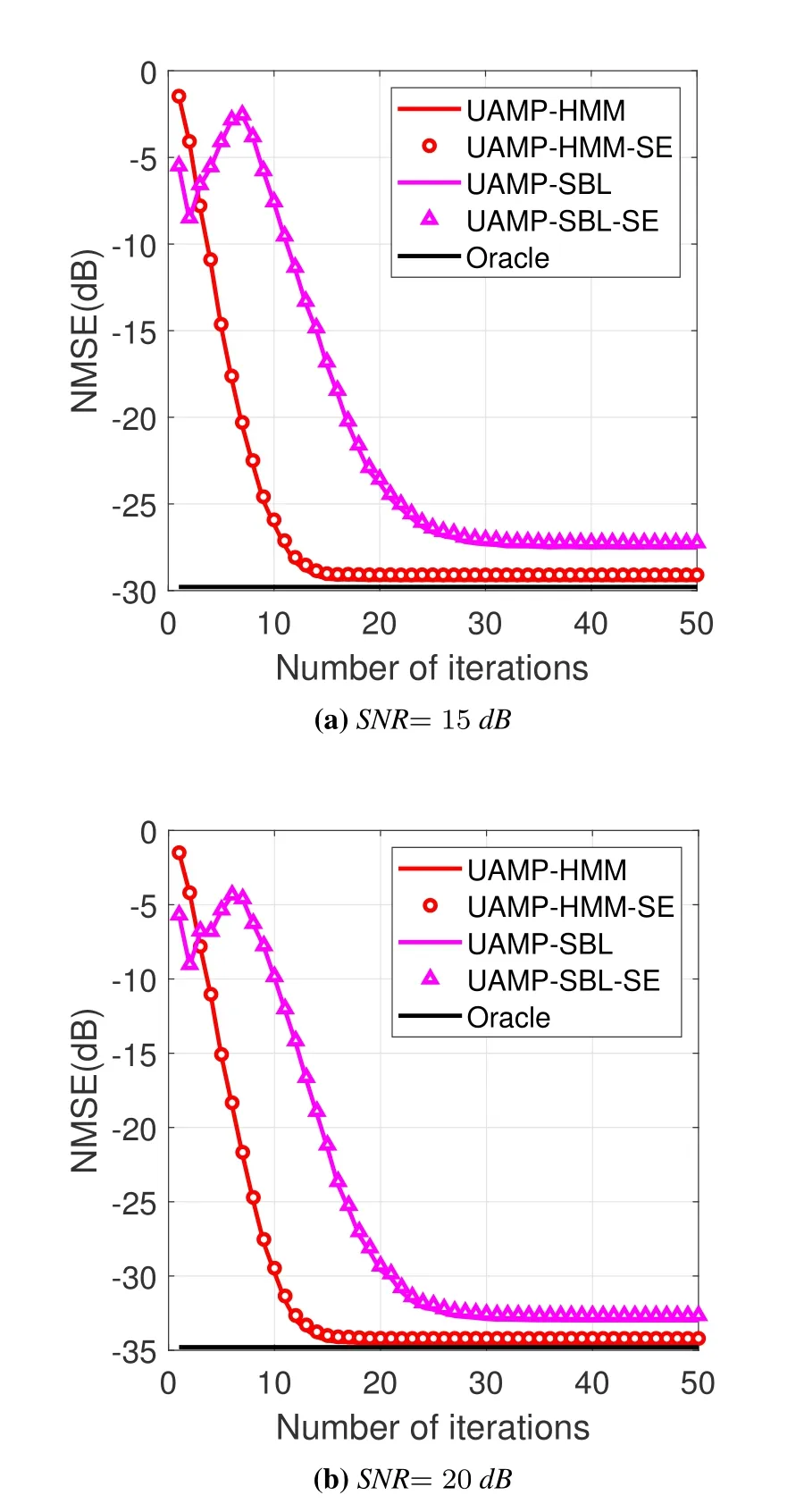
Figure 7.SE and simulated performance of UAMP-HMM and UAMP-SBL.

VI.CONCLUSION

In this paper,we study the channel estimation problem for OTFS in the presence of fractional Doppler.To do so,we propose a statistical channel model based on HMM.This model captures the support correlation in the channel as a Markov process.Next,we incorporate the HMM with UAMP algorithm to create a UAMP-HMM algorithm,which is capable of recovering the channel coefficient.To update the hyperparameters in our proposed algorithm,we derive the update criterion based on EM.Moreover,we derive the state evolution of the UAMP-HMM algorithm,providing a clear prediction of its performance.The state evolution analysis reveals that the proposed algorithm outperforms the state-of-the-art algorithms in terms of a reduced number of iterations and lower channel estimation NMSE.Through simulations,we demonstrate that our proposed UAMP-HMM algorithm,derived from the HMM prior,is able to better exploit the structured sparsity in the effective DD domain channel with fractional Doppler and achieve substantial improvements compared to various baseline algorithms.

ACKNOWLEDGEMENT

This work was supported by the Key Scientific Research Project in Colleges and Universities of Henan Province of China (Grant Nos.21A510003) and Science and the Key Science and Technology Research Project of Henan Province of China(Grant Nos.222102210053).

APPENDIX EM UPDATE EQUATIONS FOR HYPERPARAMETERS

In this part,we provide the detailed derivation of EM learning update expressions for automatically tuning the hyperparametersρ≜{p10,λ,ψh}of the UAMPHMM algorithm.

A E-Step

Letρℓdenote the set of parameter estimates at theℓ-th EM iteration.In E-step,we aim to calculate the the conditional expectation of the log likelihood of the hidden data given the observed data,r,and the current estimates of the parametersρℓ.For parameterp10andλ,we use s as hidden variable,while forψh,we use h.We defineQ(γ|ρℓ)as the conditional likelihood as a function ofγ,the parameter to be updated,e.g.

B M-Step

In this step,we maximize the expected log likelihood with respect to the model parameters to get the updated hyperparameters at theℓ+1-th iteration,i.e.

We first calculate the posteriorp(sj|r)and the joint posteriorp(sj-1,sj|r) using the sum-product algorithm based on the factor graph in Figure(3).

To solve(B.1),we differentialQs|r,ρℓ(λ|ρℓ)w.r.tλ:

Setting the equation(B.6)to zero and solving forλyields the update equation for sparsity rate:

To update the transition probabilityp10,we take the partial derivative ofQs|r,ρℓ(p10|ρℓ)w.r.tp10:

Equating the above equation to zero and solving forp10gives:

To derive the update equation for the variance of Gaussian component in the priorψh,we take the partial derivative ofQh|r,ρℓ(ψh|ρℓ)w.r.tψh:

A neat trick is employed to handle this situation.The domain of integration in eq.(B.11)is splitted into two part: Bϵ≡[-ϵ;ϵ] and its complement≡CBϵ.Substitude the above formula into(B.11)and we can get

Setting the resulted expression to zero gives: