Model-Driven Deep Learning for Massive Space-Domain Index Modulation MIMO Detection
Ping Yang,Qin Yi,Yiqian Huang,Jialiang Fu,Yue Xiao,Wanbin Tang
The National Key Laboratory of Science and Technology on Communications,University of Electronic Science and Technology of China,Sichuan 611731,China
*The corresponding author,email: yang.ping@uestc.edu.cn
Abstract: In this paper,a powerful model-driven deep learning framework is exploited to overcome the challenge of multi-domain signal detection in spacedomain index modulation (SDIM) based multiple input multiple output(MIMO)systems.Specifically,we use orthogonal approximate message passing(OAMP)technique to develop OAMPNet,which is a novel signal recovery mechanism in the field of compressed sensing that effectively uses the sparse property from the training SDIM samples.For OAMPNet,the prior probability of the transmit signal has a significant impact on the obtainable performance.For this reason,in our design,we first derive the prior probability of transmitting signals on each antenna for SDIMMIMO systems,which is different from the conventional massive MIMO systems.Then,for massive MIMO scenarios,we propose two novel algorithms to avoid pre-storing all active antenna combinations,thus considerably improving the memory efficiency and reducing the related overhead.Our simulation results show that the proposed framework outperforms the conventional optimization-driven based detection algorithms and has strong robustness under different antenna scales.
Keywords: deep learning;generalized spatial modulation;index modulation;massive MIMO;message passing orthogonal approximate
I.INTRODUCTION
Since the birth of mobile communication technology,communication technology as a kind of infrastructure for people’s production and life and industrial economy has brought great changes.Especially,at present,human society has begun to enter the era of information,digitization and intelligence.All walks of life need more advanced communication technology to enable them to support higher data rate,greater network capacity,higher spectrum efficiency,higher energy efficiency and better mobility[1,2].Multiple-input multiple-output(MIMO)is a basic yet important technology for future wireless communication systems,since it can effectively make use of resources in space domain,time domain,frequency domain and polarization domain to greatly improve the spectrum utilization rate and energy efficiency of the system[3].In recent ten years,this technology has been widely concerned by researchers for different application scenarios.However,there are also some key technical problems in large-scale MIMO,such as antenna design and placement,multiple radio-frequency(RF)chains overhead,and inter-channel interference (ICI) caused by very close antenna positions.Among them,the increase of hardware cost caused by the increase of RF chain is the main consideration of this paper.
Space-domain modulation (SM) is a lowcomplexity modulation technique for multiple antenna systems.It was proposed [4,5] to solve the problems of transmitting antenna synchronization and channel interference in MIMO systems.Its working principle is that space domain is introduced into the traditional signal domain,so that the information bit is mapped to the three-dimensional constellation.The specific process is to divide the information bit block into two parts: the antenna-bit block and the signal-bit block at each time-slot.The antenna-bit block is used to activate only one of the transmit antennas,while the other antennas are in a silent state.Then the modulation signal corresponding to the signal bit block is transmitted from the activated antenna.Therefore,the combination of SM and MIMO (SM-MIMO)can greatly reduce the number of RF chains required and hence reduce the cost of hardware.However,in order to achieve the similar transmission rate with that of conventional MIMO systems,a large number of transmit antennas need to be added,and the number of transmitting antennas must be a power of two,which is unbearable in communication scenarios requiring high transmission rates.
Therefore,in order to solve the aforementioned problem concerning the requirement on antennas for high-rate SM-MIMO applications,[6] proposed a new generalized spatial modulation (GSM) technology.Different from SM,GSM can activate multiple antennas at the same time.The disadvantage of SM can be overcome by selecting different antenna combinations from the limited transmitting antennas,and the scheme can find a good compromise between spectral efficiency and energy efficiency [7].The authors of [8] also analyzed and proved that GSM has better performance than SM-MIMO and V-BLAST systems under some channel conditions.However,although GSM technology can achieve a good balance between the number of the RF chains and the number of transmit antennas,the increase in the number of antenna combinations also greatly increases the difficulty of receiver design,especially in large-scale systems.In general,the powerful maximum likelihood(ML) [9] detection algorithm is capable of obtaining the best system performance.However,the corresponding computational complexity limits its practical applications.By contrast,although traditional linear detection algorithms,such as maximum ratio combination (MRC) [10],zero forcing (ZF) [11] and minimum mean square error (MMSE) detectors impose lower complexity,but they suffer serious performance loss,especially for massive MIMO setups.
In order to reduce computational complexity and achieve detection performance close to ML,some improved algorithms based on linear detection were proposed [12,13].Specifically,[12] proposed a ordered block minimum mean-squared error detection algorithm(OB-MMSE),which firstly uses a sorting algorithm to sort the transmitting antenna combinations.Then,MMSE detection is carried out according to the sorted antenna combination.In order to reduce the complexity of the algorithm,a threshold value is preset to judge the reliability of the detection signal.However,the OB-MMSE algorithm is sensitive to the selection of threshold.More specifically,a large threshold is easy to reduce the detection performance,while a small threshold may degenerate the OB-MMSE algorithm into the ML algorithm and the computational complexity will be greatly increased.In order to achieve a perfect balance between performance and complexity,[13] made further improvements to OBMMSE by providing an efficient sorting algorithm based on conditional ML estimation and centralized distance measure.
Furthermore,due to the inherent sparse characteristics of GSM-MIMO signals,some detection technologies based on compressed sensing (CS) [14] framework were proposed.Among them,the detection algorithms based on orthogonal matching pursuit (OMP)and basis pursuit (BP) were widely used.Specifically,in [15],an OMP-assisted normalized CS detection algorithm was applied in generalized space shift keying(GSSK)systems,which is a special form of GSM.However,[16] pointed out that the channel normalization step performed in [15] may have adverse effects on the bits transmitted by the traditional constellation symbol,so this method may not be suitable for GSM.In [17],the author proposed a basis pursuit denoising (BPDN) algorithm for GSMMIMO systems,which adopted a denoising detection scheme using sparsity to counter the influence of noise,so that the algorithm has better robustness and detection performance than other suboptimal detection algorithms in over-determined and under-determined systems.However,in[18],the authors found through simulation that when the channel has a high level of cross-correlation,the above algorithm may have large performance loss,which is especially obvious under high-order modulation schemes.Therefore,the authors of[18]proposed a two-stage enhanced Bayesian compressed sensing (EBCS) algorithm to solve the above problems and achieve better detection performance than BP with lower complexity.In addition,[19] shown that although some detection algorithms based on CS achieved superior detection performance,they also caused serious performance loss when the number of receive antennas is further reduced.Therefore,the author proposes a more robust detection algorithm based on sparse Bayesian learning framework,which can achieve better bit error rate (BER) performance than the detection algorithms proposed in[15]and [17].Other further extensions of the above algorithms are shown in[20–24].
In recent years,the rise of artificial intelligence and many important achievements in the field of communication[25–28]provide a new solution for the design of GSM-MIMO detector.For example,in [29],Yang etal.proposed a low-cost link adaptive framework for SM-MIMO system based on machine learning paradigm,which can significantly reduce complexity and achieve near-optimal detection performance compared with many traditional optimization-driven frameworks.In [30],a modular deep neural network (DNN) detection structure for antenna-bit and symbol-bit detection was proposed,which is capable of achieving BER performance close to the optimal ML detection for the scenarios with Gaussian noise or non-Gaussian noise.Moreover,[31] proposed a block DNN (B-DNN) detection structure.However,different from[30],this algorithm uses the idea of exhaustive search to design a DNN for every possible combination of antennas,and takes the result with the least loss as the final output.In general,this algorithm is only suitable for small-scale GSM-MIMO systems,since its detection complexity will greatly increase when the system scale increases.For GSM communication systems designed for visible light communications,[32]also proposed another detection structure based on DNN,which can effectively extract features from received signals and directly output the estimated information bits.As shown in [32],the BER performance obtained by the proposed algorithm is better than that of traditional detection algorithms.It should be noted that the channels used by the intelligent detection algorithm in the above literature are assumed to be static or quasi-static channels,while cannot work well in dynamic channel scenarios.Therefore,to solve this problem,[33]designed a DNN-based data-driven detection model,which would first update the channel state information (CSI) of each time slot before detecting data,and then use the updated CSI for symbol detection.Therefore,the algorithm can obtain better detection performance in dynamic channels.
Although the literature for DL-based detection problem of GSM-MIMO system made some attempts,but for now on the aspects of the research is still relatively lack.Note that the existing research basically is based on the data-driven way,which completely used the DL unit to replace the traditional detection module.Usually,these designs need huge amounts of data for training,have a large number of model parameters,and require relatively long the training time.Different from the data-driven approach,the model-driven detection algorithm takes expert knowledge into account.On the basis of some existing iterative detection algorithms,the advantages of data-driven and traditional mathematical models can be taken into account by adding some learning parameters.
To the best of our knowledge,the potential benefits of model-driven detection algorithms for massive GSM-MIMO systems have not been investigated.By contrast,considerable achievements have been made in conventional massive multiplexing MIMO systems.For example,in[34],NeevSamueletalproposed a detection model named DetNet,which combines a small amount of expert knowledge and needs to learn to optimize a neural network (NN) with a large number of parameters.In the case of independent and identically distributed Gaussian channels with low-order modulation schemes,the proposed algorithm is capable of achieving better performance than the semipositive definite relaxation algorithm,even comparable to the classic sphere decoding(SD).In[35],HengtaoHeetalintegrated NN into orthogonal approximate message passing (OAMP) algorithm and proposed an OAMPNet detection model.Compared with DetNet,this model has only two parameters to be optimized for each layer,so its stability and convergence speed are improved in the training process[34].In addition,due to the algorithm can optimize training parameters from a large amount of data,it can also achieve considerable performance improvements compared to the conventional OAMP algorithm.In order to further improve the detection performance of OAMPNet algorithm,[36] continued to improve OAMPNet on the basis of[35],and proposed OAMPNet2 detection model.Compared with OAMPNet model,the detection model added more learning parameters in each layer.This results in better BER performance than OAMPNet.
In view of the excellent performance of OAMPNet2 in massive MIMO systems and filling the gap of model-driven detection algorithm in GSM-MIMO systems,this paper considers the expansion of OAMPNet2 model to GSM-MIMO systems for improving its detection performance.The main contributions of this paper can be summarized as follows:
1.We extend the OAMPNet2 model designed for conventional MIMO systems to GSM-MIMO systems,and propose a general design framework.In order to enable the algorithm to obtain better detection performance in massive antenna scenarios,we derive the prior probability of transmit GSM-MIMO signals on each antenna.
2.In order to solve the problem of insufficient memory due to the large number of active antenna combinations in massive GSM-MIMO systems,we propose two algorithms to avoid pre-storing all active antenna combinations,thus greatly improving the memory efficiency and reducing the memory overhead.
3.We simulate and compare the BER performance of the proposed OAMPNet2 detection model and traditional detection algorithms,and analyze the influence of different antenna setups,the number of active antennas and the orders of the modulation schemes on the detection performance.The implementation results show that the OAMPNet2 detection model can greatly improve the detection performance compared with traditional detection algorithms,such as ZF and MMSE,and has better robustness for different scale systems.
The rest of this paper is organized as follows.In Section II,the system model of GSM-MIMO is introduced,and the traditional detection algorithms are briefly described.Next,Section III first introduces and deduces the principle of OAMP algorithm,and then introduces the OAMPNet2 model and its theoretical derivation on this basis.Furthermore,the prior probabilities of transmitting signals on all transmitting antennas in massive GSM-MIMO system are derived,and two algorithms to avoid storing all combinations of antennas are introduced.After that,the detection performance of OAMPNet2 is evaluated in Section IV for different simulation setups,such as different transmit rates.Finally,we summarize the paper and look forward to further research in the future in Section V.
Notation: IMdenotes anM-dimensional unit diagonal matrix.Cm×ndenotes an (m×n)-dimensional complex-valued matrix,and [·]m×ndenotes an (m×n)-dimensional matrix.E(·) is the mean of a vector or matrix.|·|and∥·∥means the absolute value and Frobenius norm of the elements,respectively.(·)Tand(·)Hrepresent the transpose and conjugate transpose operators,respectively.represents the round down operator.Re(x)and Im(x)means the real and imaginary part ofx,respectively.tr(·)represents the trace of the matrix.
II.SYSTEM MODEL
This section introduces the model of GSM-MIMO systems as shown in Figure 1.Besides,some conventional detection methods for GSM-MIMO are also introduced.

Figure 1.The basic model of GSM-MIMO systems.
2.1 GSM-MIMO System Model
As shown in Figure 1,different from the traditional SM-MIMO systems,the GSM-MIMO scheme activates a set of transmit antennas to transmit signal at a symbol period.The positions of the active antennas are determined by the index bits,thus more information bits can be carried.Assuming there areNttransmit antennas andNrreceive antennas in a GSMMIMO system,andNatransmit antennas are activated in a symbol period.In this case,the amount of different combinations of active antennas is
Then the active antennas transmit servalM-ary modulation symbols(e.g.,PSK or QAM constellations)into the receive antennas.The number of information bits that can be conveyed by the modulation symbols is
Therefore,the total number of bits per symbol in GSM-MIMO systems can be expressed as
LetAbe the set of allM-ary modulation symbols,then the transmit signal on each antenna is chosen from the set.More specifically,the transmit symbols onNtantennas x=[x1,x2,...,xNt]Tcan be expressed by
whereaiindicates the states of transmit antennas.In our design,wheni-th antenna is active,we haveai=1,otherwise,the value ofaiis 0.
Then the received signals y∈of GSMMIMO system in a symbol period can be formulated as
where H∈are the channel matrix between the transmit and receive antennas and n∈are the additive white gaussian noise (AWGN).xI∈denotes the set of the transmit signals onNaactive antennas and HI∈consists of the column vectors of H in the positions of active antennas.
The model of GSM-MIMO system in (6) can be further transformed into the real-valued version by considering the real and imaginary parts separately[36,37].
2.2 Signal Mapping Scheme for Massive GSM-MIMO
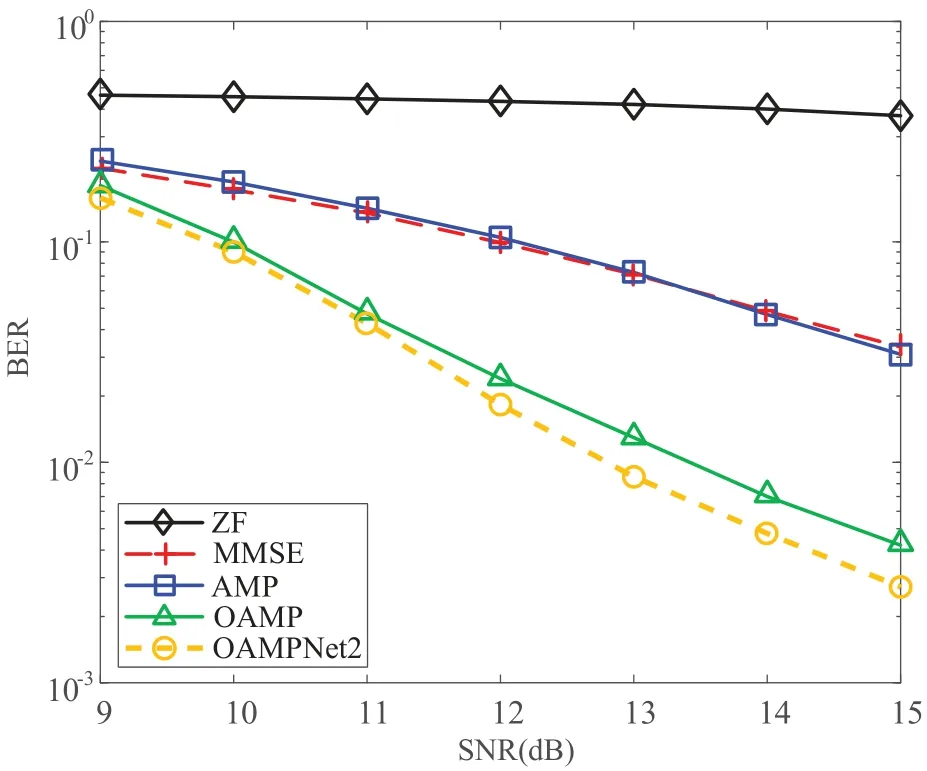
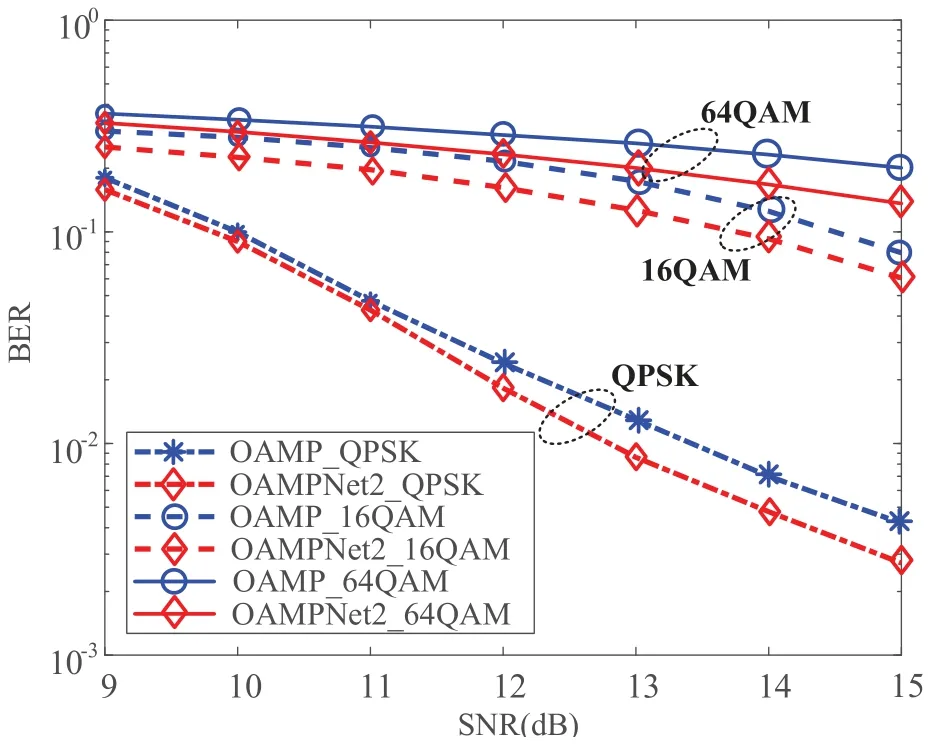
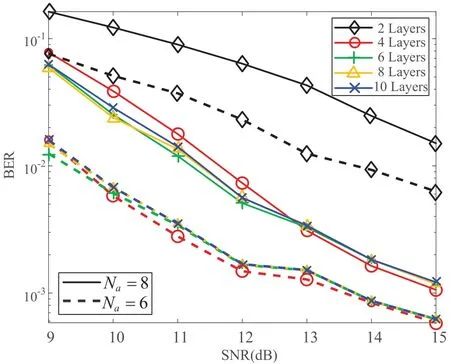
The core of GSM scheme is the mapping rule between the index bits and the positions of activated antennas.For conventional SM-MIMO systems,the amount of combinations is relatively small,so that the system can directly store all possible combinations and their corresponding index bits.However,for massive GSMMIMO systems,the number of possible combinations is extremely large(e.g.,whenNt=64 andNa=18,the amount of possible combinations is up to 251).Therefore,it is impossible for GSM-MIMO systems to store all combinations.To solve this problem,we design an iterative algorithm (Algorithm1) to map the index bits into the location of the activated antennas.InAlgorithm1,index bits biare first converted into a decimal numberd(Step 0).Thendis transformed into a combination of the locations of active antennasT=[t1,t2,...,tNa]T,1≤t1 Table 1 provides an example of the GSM scheme with the proposed mapping algorithm whenNt=4,Na=2,the modulation scheme is BPSK (M=2).In this configuration,the length of index bits isN1==2 and the length of the modulation bits isN2=Nalog2M=2.Therefore,each symbol period carriesN=N1+N2=4 information bits,the first 2 bits are index bits and the remaining bits are used for signal modulation. Table 1.An example of the proposed GSM scheme with BPSK when Nt=4 and Na=2. Based on the proposed mapping rule inAlgorithm1,the demapping rule from the detection positions of active antennasto the decimal number ˆdis then given byAlgorithm2. 2.3.1 ML Detection The optimal detection method for GSM-MIMO is maximum likelihood detection[11],given by The ML criterion requires traversing the entire search space to find one combination ofNtmodulation symbols with the smallest Euclidean distance from y.The complexity order of ML detection iswhich grows exponentially withNt,Naand.The high complexity of ML detection makes it only suitable for small-scale GSM-MIMO systems.To achieve efficient detection for massive MIMO systems,some suboptimal detection schemes with low complexity were proposed,among which the most commonly used algorithms are the linear-type ZF and MMSE detections. 2.3.2 ZF Detection In ZF,the detected symbols are directly solved by the least square method,thus avoiding the highcomplexity global search.The detected symbols with ZF scheme[13]are The ZF scheme ensures that there is no interference between symbols,but there is also the interference of noise,and the noise is affected by the matrix(HHH)-1HH.In general,the matrix amplifies the noise when the signal-to-noise ratio(SNR)is low. 2.3.3 MMSE Detection If the statistics of the transmitted signals are known,the ZF mechanism can be further improved to MMSE detection mechanism.More specifically,assuming the transmitted symbols are independent and follow the Gaussian distribution,then the MMSE detection scheme can be formulated as As can be observed by comparing(13)and(14),the MMSE criterion adds a termto the inverse matrix,which can effectively suppress the influence of the noise when the SNR is poor,so as to improve the detection performance. In this section,we introduce the OAMP algorithm and then describe the OAMPNet2 model in detail.After presenting the principle of the OAMPNet2 detection,the prior probabilities of the signals emitted on all transmitting antennas in the system are derived and the two proposed algorithms to avoid storing all antenna combinations are investigated. OAMP is a low-complexity signal recovery algorithm in the field of compressed sensing.The OAMP algorithm contains two parts: linear estimation and nonlinear estimation.Algorithm3 summarizes the OAMP-based detection algorithm for conventional MIMO systems. Denoting the estimated of x by,and the elements ofare independently and identically distributed satisfying wherevdenotes the statistical variance between the actual and estimated values. 1)ErrorCalculation: In order to measure the accuracy of linear and nonlinear estimation,we define the error vectors as Therefore,the error variance can be expressed as and they are calculated by Eqs.(16)and(17),respectively. 2)LinearEstimation: The linear estimation of x is denotes by(15),where The matrix Wtin Eq.(24) can be the transpose of,the pseudo-inverse of,or the linear MMSE matrix.According to[37],we can obtain the optimal Wtwhensatisfies 3)NonlinearEstimation: The nonlinear estimation is represented as(18).Since MIMO has the same prior probability on each transmitting antenna,the prior distributionP(xj) of the transmitted symbol and expressed as forj=1,2,...,2Nt.We consider the nonlinear estimation is the MMSE denoiser,which can be given as The accuracy and convergence of the estimation resultsare determined by the prior mean r(t)and variance.The OAMP-based algorithm adopts an iterative approach to obtain r(t)and,and we choose the DL-based algorithm to get appropriate step size in order to improve performance. The OAMPNet2 is an improved model of the OAMP algorithm based on DL.It improves the performance of the OAMP algorithm by unfolding the iterative process of the OAMP algorithm,simulating each iteration using the network layer of DL,adding optimization parameters in each layer,and finally improving the performance of the OAMP algorithm through training and continuous optimization of these parameters.The structure of the OAMPNet2 is illustrated in Figure 2. Figure 2.The structure of the OMPNet2 network. The network consists ofTnetwork layers,each with the same network structure,the only difference being the different values of the trainable parameters.As shown in Figure 1,each iteration of the OAMP algorithm is mapped to each layer of the OAMPNet2 network.For thetth layer of OAMPNet2,the input is the estimated signal from the (t-1)th layer.Therefore,its signal detection step can be expressed as where Ctis an improvement of Btby adding a learning parameterθtthat adjusts the error varianceSimilar to the OAMP algorithm,we analysis the error calculation,linear and nonlinear estimations,and learnable parameters in OAMP-Net2 as follows: • Error Calculation: The error variance estimatorsandare used to evaluate the accuracy of linear and nonlinear estimates in OAMPNet2,respectively.The error varianceof OAMPNet2 is calculated from (29),which is the same as that of the OAMP method.The error varianceof OAMPNet2 is denoted as(31),which adds the learnable variableθtcompared to the OAMP scheme. • Linear Estimation: The linear estimation of OAMPNet2 is calculated by(28),which adds the learnable parameterγtto the OAMP algorithm.Comparing Eqs.(15) and (28),it can be found thatγtcorresponds to the step size for updating the linear estimation r(t).In the OAMP algorithm,a fixed iteration step size is used for each iteration,i.e.,γt=1.OAMPNet2 obtains better performance by adopting a suitable step size in each iteration. • Nonlinear Estimation: The nonlinear estimationof OAMPNet2 is computed by (33),which adds the linear estimation r(t)and the learnable parametersϕtandξtto (18).Whenϕt=1 andξt=0,the nonlinear estimator of OAMPNet2 is equivalent to the MMSE estimator of OAMP. • Learnable Parameters: Moreover,we can find that different fromAlgorithm1,the OAMPNet2 includes four learnable variables for each layer.The learnable variables attth layer is denoted byΩt={γt,ϕt,ξt,θt}.In particular,the OAMPNet2 method is equal to the OAMP algorithm whenγt=ϕt=θt=1 andξt=0.The learnable variables of theT-layer OAMPNet2 network can be represented as Ω=,and the number of parameters of the network is 4T. OAMPNet2 can adjust the parameter Ω according to the actual environment,which can adapt to different channel environments and achieve satisfactory performance.In addition,the number of parameters of OAMPNet2 is not related to the number of antennas but only determined by the number of layersT,which is advantageous for the detection under large-scale antennas. In this subsection,we first re-derive the prior probability of the transmit signal based on the GSM-MIMO system model.Then,we discuss GSM-MIMO detection based on OAMPNet2.Finally,we analyze the complexity of the proposed scheme and the existing schemes. 1)PriorProbabilitiesofTransmittingSignals: Unlike the massive MIMO system,not every antenna is active in the GSM-MIMO system.Therefore,the prior probability of the transmitted signal at each antenna in this system is different from the prior probability of the massive MIMO system.However,the derivation of the OAMP algorithm shows that the prior probability of the transmit signal has a significant impact on the performance of the OAMPNet2 algorithm.Therefore,the algorithm first needs to calculate the prior probabilities of all transmit antenna signals in GSM-MIMO. Since each transmitting antenna has two states,active and inactive.Denoting the active state of theith antenna byai,we have Therefore,we can obtain the prior probability of transmitting signals on each antenna in GSM-MIMO systems by Therefore,the nonlinear estimation part of OMAPNet2 in GSM-MIMO can be rewritten as Based on(39),the corrected estimates are obtained at each layer of OAMPNet2 network. 2)TheOAMPNet2forGSM-MIMODetection:OAMPNet2 is adoptd to solve the GSM-MIMO detection problem,which includes offline training phase and online detection phase of OAMPNet2.We represent the training dataset aswhereHere,˜H(m) andstand for the input and label of themth data pair,respectively,andDindicates the size of the training dataset.We consider the mean square error(MSE)function as the loss function,which can be expressed as whereLtanddenote the loss function and output of thetth layer OAMPNet2 network,respectively. In the offline training phase,the parameters Ω=of the OAMPNet2 network are optimized by minimizing Eq.(40).In the online detection phase,the estimated signalis obtained by feeding the received signaland the channel matrixto the trained OAMPNet2 network,where(T)is the output of the last layer of of OAMP network.The unmapping process ofis as follows • Step 1: Convert the estimated signalin the realvalued domain to the signalin the complexvalued domain. • Step 2: Sort all elements inaccording to their power. • Step 3: Select the index corresponding to the firstNaelements with the largest power,and consider them as the activated antennas. • Step 4: Get the corresponding antenna activation pattern(AAP). • Step 5:Demodulate the corresponding AAP to,which requires converting the estimated antenna combinationto decimaland then to.This process can be performed by theAlgorithm2. • Step 6: Demodulate the detected signal on the activated antennas to,which can be obtained according to the constellation demapping. 3)ComplexityAnalysis: We analyze the computational complexity of the proposed OAMP-Net2 scheme and other existing schemes.Since OAMPNet2 is constructed based on the OAMP algorithm,the computational complexity of the OAMPNet2 and the OAMP algorithm is the same.Their computational complexity is mainly determined by the matrix inverse in(25)and the number of layersT,which can be expressed asThe computational complexity of the AMP algorithm isAccording to(12),the complexity of ML can be represented byThe ZF and MMSE algorithms have a complexity ofas one matrix inversion is needed. This section provides numeral simulation results to verify the BER performance of the proposed OAMPNet2 detection algorithm in GSM-MIMO systems with different MIMO setups.Besides,we also investigate the influence of some important parameters on the system BER performance through simulations,including the number of activated antennasNa,the modulation scheme and the number of network layers.In our simulations,dynamic Rayleigh channels are considered.Some parameters of the proposed OAMPNet2 detection algorithm are shown in Table 2.We train the channel data of each SNR separately to obtain the network parameters of OAMPNet2 and then use them for testing,where the size of the testing set is 1000 and the number of epochs is 30. Table 2.Parameters of the proposed OAMPNet2 detection algorithm. We first simulate a small-scale GSM-MIMO system with different detection schemes,where QPSK modulation is adapted.The results are shown in Figure 3,whereNt=Nr=4(denoted by 4×4),Na=2 and the number of OAMPNet2 layers is 10.As can be seen from Figure 3 that compared with the traditional ZF,MMSE and AMP algorithms,the proposed OAMPNet2 algorithm greatly improves the system BER performance.Besides,compared with the OAMP algorithm,the OAMPNet2 algorithm also has a considerable performance gain. Figure 3.BER comparisons of a 4 × 4,Na=2 GSMMIMO system with ZF,MMSE,AMP,OAMP and proposed OAMPNet2 detection algorithms,QPSK modulation. Then we simulated a GSM-MIMO system with antenna setup 32×32 and the number of active antennaNa=10 to further validate the performance of different detection algorithms in massive antenna system.Figure 4 shows the simulation results with BPSK modulation,the number of OAMPNet2 layers is also 10.From Figure 4,we can observe that from SNR=4 dB,OAMPNet2 starts to show a huge performance gain compared to the conventional ZF and MMSE.Specifically,when BER=0.2,OAMPNet2 has a performance gain of 5 dB compared with MMSE algorithm.Moreover,the performance advantage of OAMPNet2 becomes more prominent with the increase of SNR.In addition,OAMPNet2 algorithm also outperforms OAMP algorithm in terms of BER performance owing to the introduction of learning parameters.By comparing Figures 3 and 4,it is demonstrated that the OAMPNet2 algorithm has strong robustness under different GSM-MIMO scales,and its detection performance far outperforms the traditional detection algorithms. Figure 4.BER comparisons of a 32×32,Na=10 GSMMIMO system with ZF,MMSE,AMP,OAMP and proposed OAMPNet2 detection algorithms,BPSK modulation. Figure 5 simulates an OAMPNet2 algorithm with 10 layers for 32×32 GSM-MIMO system with different number of active antennas.Here,the modulation scheme is QPSK.Figure 5 indicates that the number ofNagreatly affects the system BER performance.Specifically,when the value ofNais small,we can obtain better BER performance.This is because a smaller the value ofNameans a fewer number of active antenna combinations in GSM-MIMO system,which is beneficial to detect the correct antenna combination.However,a small value ofNaalso leads to the decrease of transmission rate.Therefore,a tradeoff between BER performance and transmission rate should be considered when choosing the value ofNa. Figure 5.BER comparisons of a 32×32 GSM-MIMO system with proposed OAMPNet2 detection algorithm under different numbers of Na,QPSK modulation. We continue to test the impact of modulation orderMon the BER performance of OAMPNet2 algorithm assisted 32×32,Na=10 GSM-MIMO system and the results are shown in Figure 6.The number of OAMPNet2 layers is still set to be 10.As shown in Figure 6,the proposed OAMPNet2 algorithm outperforms OAMP algorithm both in low-order and highorder modulation systems.Therefore,the proposed OAMPNet2 algorithm can adapt to the change of modulation orders. Figure 6.BER comparisons of a 32×32,Na=10 GSMMIMO system with proposed OAMPNet2 detection algorithm under different modulation orders. In the above simulations,the number of OAMPNet2 layers is set to be a fixed value 10.Thus,the influence of the number of network layers is unknown through Figures 4 to 6.To this end,we further simulate the BER performance of a 32×32 GSM-MIMO systems with different number of network layers and the results are in Figure 7.As can be observed from Figure 7,in the two of GSM-MIMO systems with different values ofNa,when the number of layers is set to 4,OAMPNet2 has obvious performance gain compared with the number of layers is 2,and the performance is not much different from that when the number of layers is 6,8 and 10.A lower number of network layers leads to a lower complexity order.Therefore,OAMPNet2 can achieve a suitable compromise between detection performance and computational complexity when the number of layers is 4. Figure 7.BER comparisons of two 32×32 GSM-MIMO system with proposed OAMPNet2 detection algorithm under different network layers,QPSK modulation. In this paper,we proposed a novel framework for model-driven deep learning aided massive GSMMIMO systems,where the OAMP technique is used as the main structure and the characteristics of the GSMMIMO signals,such as the sparse property as well as the active antenna combinations,are jointly exploited for efficient detections.Through the computational complexity and BER comparisons among the comparative schemes,we provided an insight into the promising benefits of combing machine learning and multidomain modulations.We believe that its reconstruction quality can be further improved by using advance learning methods and hope this research encourages further study in this direction. This work is supported by the National Natural Science Foundation of China under Grant U19B2014,the Sichuan Science and Technology Program under Grant 2023NSFSC0457,and the Fundamental Research Funds for the Central Universities under Grant 2242022k60006.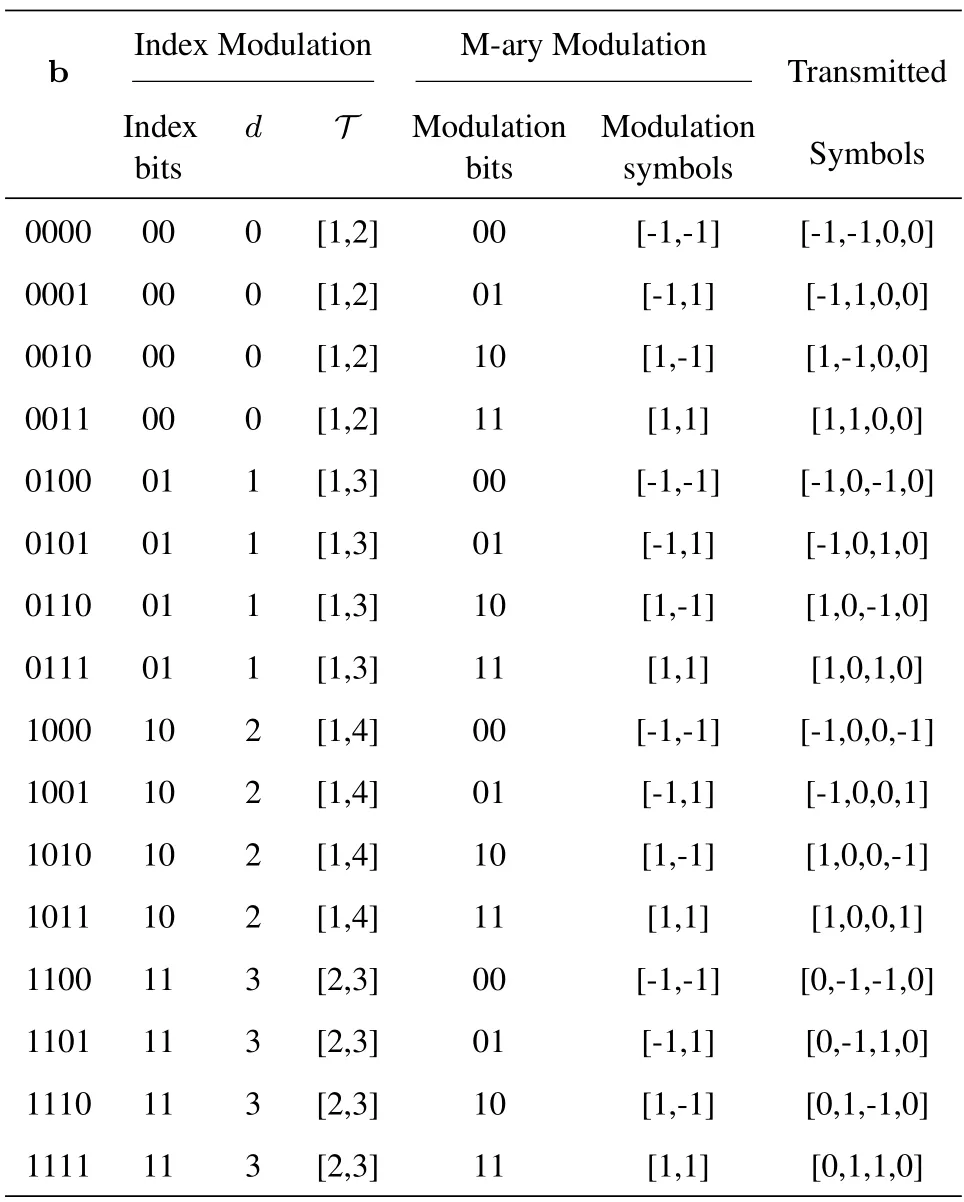
2.3 Conventional Detection Methods for GSM-MIMO


III.MODEL-DRIVEN DL-BASED SIGNAL DETECTION
3.1 OAMP-Based Detection Method
3.2 OAMP-Net2 Detection Method

3.3 Proposed OAMP-Net2 Method for GSMMIMO Detection
IV.SIMULATION RESULTS



V.CONCLUSION
ACKNOWLEDGEMENT
- China Communications的其它文章
- SR-DCSK Cooperative Communication System with Code Index Modulation: A New Design for 6G New Radios
- Sparsity Modulation for 6G Communications
- Sparse Rev-Shift Coded Modulation with Novel Overhead Bound
- Reconfigurable Intelligent Surface-Based Hybrid Phase and Code Modulation for Symbiotic Radio
- Modulation Recognition with Frequency Offset and Phase Offset over Multipath Channels
- UAMP-Based Delay-Doppler Channel Estimation for OTFS Systems

