System Outage Probability and Diversity Analysis of a SWIPT Based Two-Way DF Relay Network Under TransceiverHardware Impairments

Guangyue Lu ,Zhipeng Liu,2,* ,Yinghui Ye ,Xiaoli Chu

1 Shaanxi Key Laboratory of Information Communication Network and Security,Xi’an University of Posts and Telecommunications,Shaanxi 710061,China

2 Key Laboratory of Universal Wireless Communications,Beijing University of Posts and Telecommunications,Beijing 100876,China

3 Department of Electronic and Electrical Engineering,University of Sheffield,U.K.

*The corresponding author,email: zhipengliu_steve@163.com

Abstract: This paper investigates the system outage performance of a simultaneous wireless information and power transfer (SWIPT) based two-way decodeand-forward(DF)relay network,where potential hardware impairments (HIs) in all transceivers are considered.After harvesting energy and decoding messages simultaneously via a power splitting scheme,the energy-limited relay node forwards the decoded information to both terminals.Each terminal combines the signals from the direct and relaying links via selection combining.We derive the system outage probability under independent but non-identically distributed Nakagami-m fading channels.It reveals an overall system ceiling (OSC) effect,i.e.,the system falls in outage if the target rate exceeds an OSC threshold that is determined by the levels of HIs.Furthermore,we derive the diversity gain of the considered network.The result reveals that when the transmission rate is below the OSC threshold,the achieved diversity gain equals the sum of the shape parameter of the direct link and the smaller shape parameter of the terminalto-relay links;otherwise,the diversity gain is zero.This is different from the amplify-and-forward (AF)strategy,under which the relaying links have no contribution to the diversity gain.Simulation results validate the analytical results and reveal that compared with the AF strategy,the SWIPT based two-way relaying links under the DF strategy are more robust to HIs and achieve a lower system outage probability.

Keywords: decode-and-forward relay;diversity gain;hardware impairments;simultaneous wireless information and power transfer;system outage probability

I.INTRODUCTION

Owing to its high spectrum efficiency,two-way relay networks (TWRNs),which achieve bidirectional message exchange between two terminals via a relay node,are gaining significant momentum in the area of Internet of Things [1].However,the development of TWRNs is facing challenges,particularly due to the limited battery capacity of the relay node [2].To address this issue,simultaneous wireless information and power transfer(SWIPT)technique has been integrated into TWRNs,which can be applied in wireless sensor networks to enhance the communication quality between sensors[3].The key idea of SWIPT based TWRNs is to allow the energy-limited relay node to harvest energy from incident radio frequency(RF)signals through either a time switching (TS) or power splitting (PS) scheme,and use the harvested energy to assist the transmission between two terminals [4].The design of PS or TS schemes and the performance analysis for SWIPT based TWRNs have been studied[5–15].

For a PS-SWIPT enabled two-way decode-andforward (DF) relay network under a time division broadcast(TDBC)protocol,the authors in[5]studied the terminal-to-terminal (T2T) outage performance.Shietal.[7] considered a two-way DF relay network under a TDBC protocol,and proposed a dynamic PS scheme to enhance system outage performance.Considering a SWIPT based two-way DF relay network,the authors in [9] investigated the tradeoff between the achievable data rate and the residual harvested energy at the relay node.In [11],the authors considered a SWIPT enable cognitive TWRN under a multiple access broadcast (MABC) protocol,and jointly optimized the PS ratio and interference temperature apportioning parameters to maximize the achievable throughput.For a two-way DF relay system under a TDBC protocol,the authors in [13] derived the system outage probability,and then studied the influence of various parameters on system outage performance.Yeetal.[15]considered a SWIPT based two-way multiplicative amplify-and-forward(AF)relay network under a TDBC protocol,in which a dynamic asymmetric PS strategy was proposed to optimize the system outage performance.Nonetheless,all the above works assumed ideal hardware,but in practical system,all transceivers always suffer from a variety of hardware impairments (HIs),e.g.,quantization error,inphase/quadrature (I/Q) imbalance and phase noise[16–20].Despite sophisticated mitigation algorithms,the residual HIs may still have a deleterious impact on the achievable performance[17].

Several recent works on SWIPT based TWRNs have taken HIs into account [21–24].For two-way cognitive relay networks,the authors in[21,22]studied the impact of HIs on the T2T outage performance with a TS or PS scheme respectively.For a TS-SWIPT based TWRN under a MABC protocol,the authors in[23]considered HIs,and studied the T2T outage performance.The results in [21–23] show that HIs deteriorate the T2T outage performance,particularly inhigh-rate transmissions.Recall that the system outage probability,which jointly considers the outage evens of both terminals and the correlation between the two links,is also critical to designing practical systems.The authors in[24]studied the system outage performance for a SWIPT based two-way AF relay network under HIs.Their theoretical analysis and simulations revealed that the relaying links contribute zero diversity gain because the AF strategy amplifies the signals and distortion noises simultaneously.On the contrary,the DF strategy has the advantage of eliminating noise accumulated at the relay node,and thus the distortion noise amplification can be avoid.Based on the above observations,a natural question arises: can this property alleviate the impact of HIs and bring performance gains in terms of the system outage probability and the diversity gain by comparing it with the AF strategy?

In this paper,we aim to answer the above questions.More specifically,we consider a PS-SWIPT based two-way DF relay network under a TDBC protocol1,where HIs at all transceivers are considered,and investigate the system outage probability2and the achievable diversity gain.

The main contributions are summarized below.

• Considering the impact of HIs,we obtain a closed-form expression for the system outage probability under independent but non-identically distributed (i.n.i.d.) Nakagami-mfading channels.The derived system outage probability reveals an overall system ceiling(OSC)effect,i.e.,when the target rate exceeds an OSC threshold that is determined by the HIs levels,the system falls into outage.It is worth noting that,different from a SWIPT based AF TWRN that suffers from not only the OSC effect but also the relay cooperation ceiling(RCC)effect caused by HIs[24],the SWIPT based DF TWRN sees only the OSC effect.

• We derive the achievable diversity gain,which equals either zero or the sum of the shape parameter of the direct link and the smaller shape parameter of the terminal-to-relay links.This is quite different from the AF strategy,where the diversity gain from the relaying links is always zero.

• The analytical and simulation results reveal the following insights.The optimal PS ratio,which minimizes the system outage probability,increases as the channel quality of the relaying links improves.The relaying links under the DF strategy are more robust to HIs than that under the AF strategy.In the presence of HIs,the SWIPT based TWRN under the DF strategy outperforms that under the AF strategy in terms of the system outage probability.

In this paper,the important notations have been summarized in Table 1.

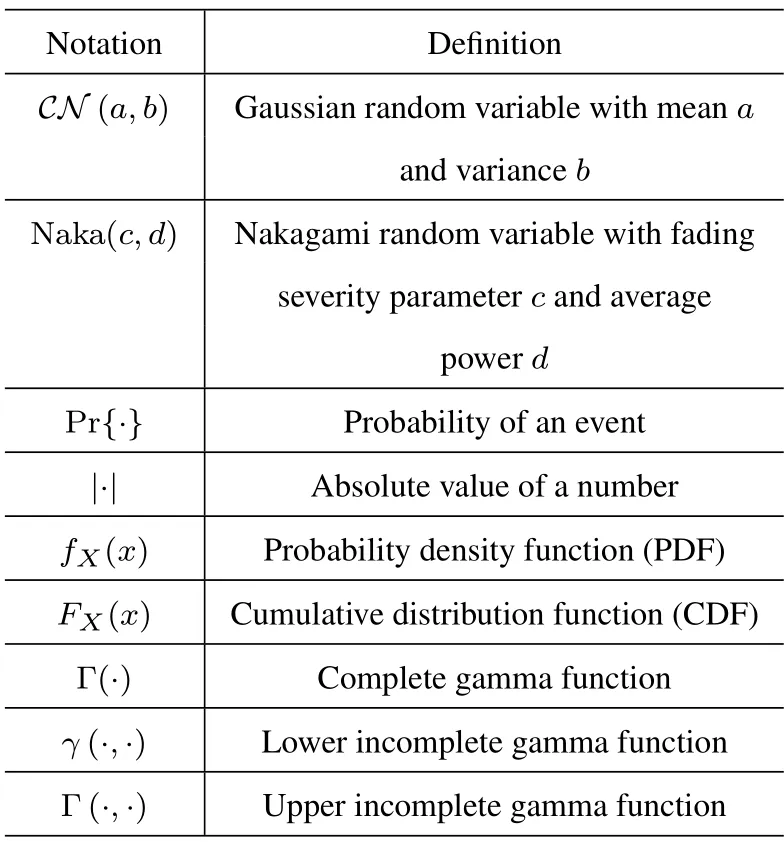
Table 1.Notations in this paper.

II.SYSTEM MODEL AND WORKING FLOW

2.1 System Model and Channel Model

We consider a SWIPT based two-way DF relay network under a TDBC protocol,where terminalSacommunicates with terminalSbwith the aid of an energylimited relayR,as shown in Figure 1.Herein,Rharvests energy from the incident RF signal following a PS scheme and a harvest-then-forward protocol.We assume that all nodes are equipped with a single antenna and operate in the half-duplex mode.

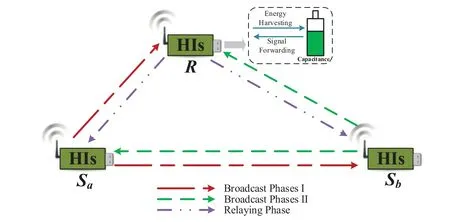
Figure 1.Model for the SWIPT based two-way DF relay network under a TDBC protocol.

In the TDBC protocol,each transmission blockTis split into three phases,viz.,two broadcast(BC)phases(each of durationT/3) and one relaying (RL) phase(T/3).During the first BC phase,Satransmits its signalxatoRandSb.In the second BC phase,Sbbroadcasts its signalxbtoRandSa.After receiving the signal fromSaorSb,Rsplits it into two parts,i.e.,one part is for energy harvesting(EH)and the other is for information decoding (ID).During the RL phase,Rcombines the decoded signalsxaandxbusing the bit-wise XOR based encoding [23],and then broadcasts the combined signal toSaandSbusing the total harvested energy.

We assume that all channels are quasi-static and reciprocal,Specifically,hij∼Naka(md,Ωd) andhir∼Naka(mi,Ωi)represent the channel fading coefficients of theSi→SjandSi→Rlinks,respectively,withi,j∈{a,b},i≠j.Sincehijandhirfollow the Nakagami distribution,the corresponding channel gains|hij|2and|hir|2follow independent and non-identical gamma distributions,and their PDF and CDF are expressed as

wheremandθdenote the shape parameter3and the scale parameter of random variableV,respectively,.Specially,whenV=|hij|2or |hir|2,m=mdormi,andθ=Ωd/mdor Ωi/mi,respectively.

2.2 Working Flow

As mentioned above,SaandSbbroadcast the signalsxaandxbin the first second BC phases respectively.For the direct link(Si→Sj,i,j∈{a,b},i≠j),as

illustrated in Figure 2,the received signal atSjfromSi,in the presence of HIs,can be expressed as[23]

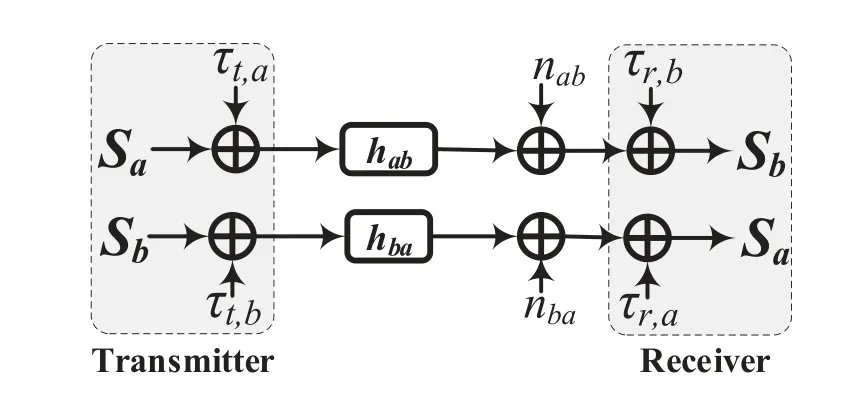
Figure 2.The signal flow diagram of the direct link under HIs.

wherexiis the signal transmitted bySiwithPi=represents the distortion noise generated by the transmitter ofSi4,τr,j∼represents the distortion noise generated by the receiver ofSjandnij∼CN(0,σ2)is the additive white Gaussian noise (AWGN) atSj.Note thatk1andk2characterize the HIs levels of the transmitter and receiver,respectively,and are assumed to be the same for each transceiver[17].For simplicity,we assume thatPa=Pb=Po[13].

Based on(3),the signal-to-noise-plus-distortion ratio(SNDR)atSjfrom the direct link is written as

whereρ=denotes the input signal-to-noise ratio(SNR).

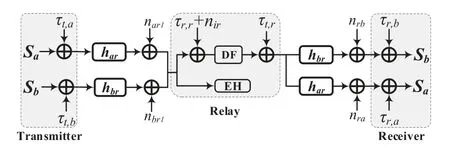
Figure 3.The signal flow diagram of the relaying link under HIs.

Using the PS protocol,the received signal yiis split into two parts via a PS ratio β (0 <β <1):for EH and 1-βyirfor ID.Thus,all the harvested energy during the two BC phases can be expressed as[23]

whereη∈(0,1) denotes the energy conversion efficiency.Based on(6),the transmit power atRcan be calculated as

Furthermore,at the relayR,the received signal fromSiused for ID can be written as

whereτr,r∼represents the distortion noise5generated by the receiver ofRandnir∼CN(0,σ2)is the AWGN atR.

Based on (8),the SNDR for decodingxiatRis given by

If bothxaandxbare successfully decoded during the two BC phases,Rperforms bit-wise XOR based encoding to obtain the re-encoded signalxr,i.e.,xr=xa⊕xbwithPr=[23].ThenRbroadcasts the signalxrto both terminals in the RL phase.Accordingly,the received signal atSifromRcan be written as

According to (10),the SNDR atSifrom the relay link can be expressed as

Following the selection combining scheme,the endto-end SNDR atSican be written as

wherei,j∈{a,b},i≠j.

III.SYSTEM OUTAGE PERFORMANCE ANALYSIS

In this section,we first derive the system outage probability in closed-form,then identify the OSC effect,and study the achievable diversity gain of our studied network.

3.1 System Outage Probability

The outage event occurs if the data rate RafromSatoSband/or the data rate RbfromSbtoSafalls below a threshold Rth[7].Hence,the system outage probability,Pout6,can be written as

Next,we derive P1and P2to obtain the closed-form expression for Poutrespectively.The first term of(14),P1,can be calculated as

Proof.See Appendix A.

The second term of(14),P2,can be calculated as

Remark 1.Asillustratedin(20),HIsdeterioratethe systemoutageperformancebyimposingaconstraint onγth.Inparticular,whenγth<,boththe directandrelayinglinksparticipateintheinformationexchangebetweentwoterminals.However,when γth≥,theoverallsystemceasesnomatterwhat theinputSNRis.ThiseffectisreferredtoasOSC,anddenotesthecorrespondingOSCthreshold.ThisceilingeffectisduetothefactthattheinstantaneousSNDRsatSa,SbandR,givenin(4),(9)and(11),areupperboundedbyγij,γir,γrj<,respectively,i,j∈{a,b}andi≠j.Inaddition,itis obviousthatthemaximumachievableSNDRthresholddecreaseswiththeincreaseoftheHIs levels.

3.2 Diversity Gain

Referring to[25],the achievable diversity gain of the considered network can be given as

Substituting(20)into(21),the diversity gain can be calculated as

Proof.See Appendix C.

Remark 2.Eq.(22)revealsthefollowingfacts.When γthexceedstheOSCthreshold,vie.,thediversitygainoftheoverallsystemisequalto zero.When,thediversitygainisthe sumoftheshapeparameterofthedirectlinkand thesmallershapeparameteroftheterminal-to-relay links.Inotherwords,boththedirectandrelayinglinks jointlyenhancethediversitygain.However,forthe AFstrategy,HIsmakesthediversitygainfromthe relayinglinkszero[24].Thereasonisasfollows.FortheAFstrategy,oneobservationfrom[[24],eq.(10)]isthattheSNDRoftherelayinglinkathigh ρisafunctionofchannelfadingcoefficients,which cannotensurethattheSNDRislargerthanitsthresholdwithprobabilityoneeventhoughρ→∞.Accordingly,theachievablediversitygainofAFrelay-inglinksequalszero.Sucharesultismainlydueto thefactthattheAFstrategyamplifiesthesignalsand distortionnoisessimultaneously.However,intheDF relaying,theSNDRsofboththerelayandterminalsat highρkeepconstant,i.e.,γir=γrj=.When γth<,theoutageprobabilityfortherelaying linksapproacheszerowiththeincreaseofρ,whichallowstherelayinglinkstocontributetothediversity gain.

IV.SIMULATION RESULTS

In this section,numerical results are provided to validate the correctness of the above theoretical analyses.Hereinafter,unless otherwise specified,the simulation parameters are set as Table 2[23,24,26].

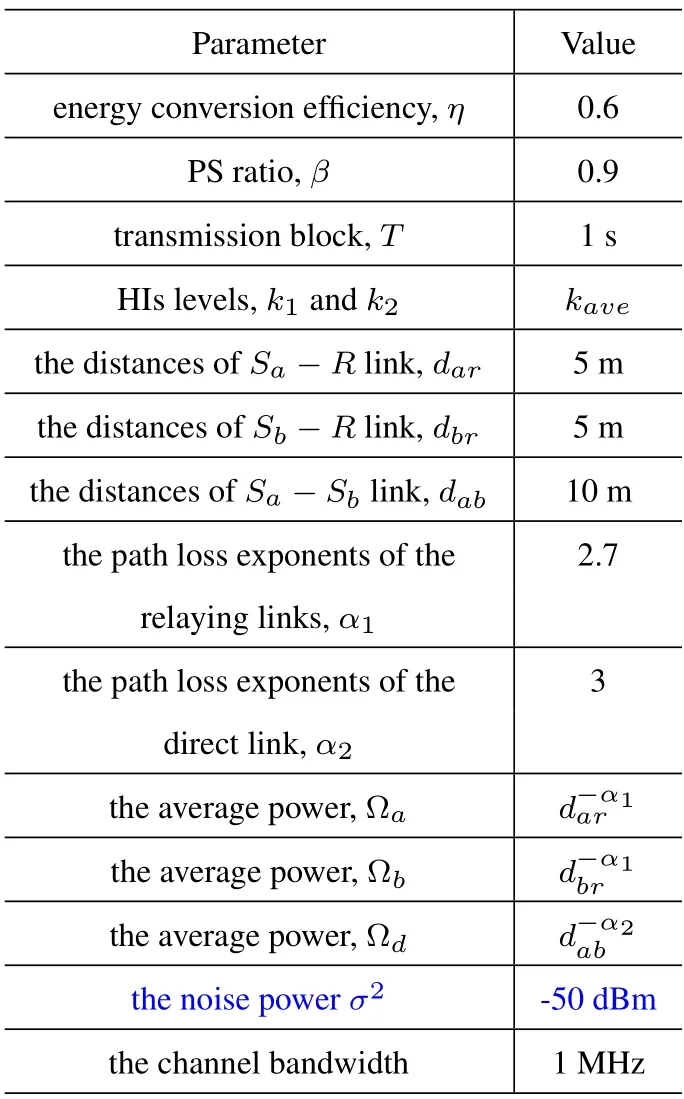
Table 2.Simulation parameters.

Figure 4 verifies the derived system outage probability in all two cases of the (20).Based on the used simulation parameters,we determine the specific value for the OSC threshold,viz.,=50.In addition,we also consider four different transmission rates i.e.,Rth=1,1.5,2 and 2.5 bit/Hz.On the basis of the definition in(13),the corresponding SNDR thresholds are calculated as 7,22,63,and 180 respectively.According to (20),when the SNDR thresholdγth=7&22 or 63&180,the corresponding system outage probability is expressed asor 1.As presented in Figure 4,the ‘♢,□,▽,◦’marked curves (analytical results)match precisely with the‘-’marked curves(simulation results) across the entire region,which validates the correctness of the derived system outage probability in Section 3.1.

Figure 4.The derived system outage probability Pout vs.the transmit power of each terminal Po,in comparison with simulation results,where kave=0.1 and{ma,mb,md}={2,2,1}.

In Appendix B,the Gaussian-Chebyshev quadrature approach is adopted to obtain the approximate system outage probabilityin(20)whenTo illustrate the performance of the Gaussian-Chebyshev quadrature approximation approach,Figure 5 shows the relative approximation error against the tradeoff parameterNfor different transmit power of each terminal.Specially,the relative approximation errorδequals the ratio of the absolute value of difference between the simulation and analytical results to the simulation result,in which the simulation and analytical results are obtained by compute simulation and(20)respectively.From Figure 5,one can observe thatδgradually approaches zero asNincreases.For instance,whenPo=-5 dBm andN=16,the correspondingδis 0.002746,which demonstrates that the Gaussian-Chebyshev quadrature with few terms can evaluate the system outage performance precisely.

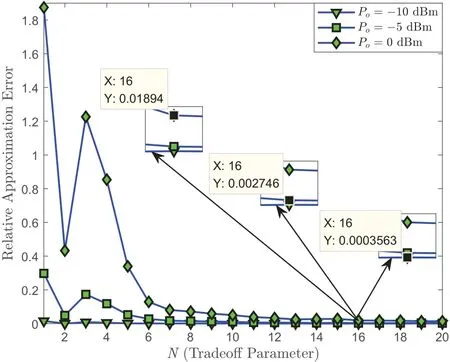
Figure 5.The relative approximation error vs. the tradeoff parameter N,where kave=0.1,Rth=1 bit/Hz and{ma,mb,md}={2,2,1}.

Figure 6 presents the system outage probability versus transmit power of each terminalPofor four transmission protocols,viz.,the TDBC with DF strategy(viz.,the considered network),the TDBC with AF strategy[24],the direct transmission,and the MABC.Herein,we ensure that the used target transmission rate satisfiesγth<.As given in Figure 6,the considered network achieves the higher system outage performance than both the MABC and the direct transmission.One can also note that the system outage performance of the considered network outperforms that of the TDBC with AF strategy.This suggests that under the presence of HIs,the DF strategy is superior to AF strategy in terms of system outage performance.Additionally,it can be observed that,for the given shape parameters,the considered network exists a performance gap between the curves corresponding to ideal hardware (kave=0) and HIs (kave=0.1),which concludes that the HIs degrade the system outage performance to some extent.Finally,as expected,better channel quality of the relaying links can significantly improve the system outage performance for the considered network under a fixed HIs level.

Figure 6.The system outage probability Pout vs. the transmit power of each terminal Po,where Rth=1 bit/Hz.

Figure 7 verifies the derived diversity gains in all two cases of the (22).Given two points (x1,y1) and(x2,y2) in the “△”or “⋄”marked curve in Figure 7,we can calculate the slope of the curve as -2 or 0 by,which is consistent with the derived diversity gain in Section 3.2.Additionally,as presented in this figure,when the target transmission rate is below the OSC threshold,both the direct and relaying links of the considered network jointly contribute to the diversity gain.However,the achievable diversity gain of the TDBC with AF strategy is only determined by the direct link.This is due to the relay node using AF strategy amplifies the distortion noises caused HIs,which in turn results in that the relaying links have no contribution to the diversity gain.

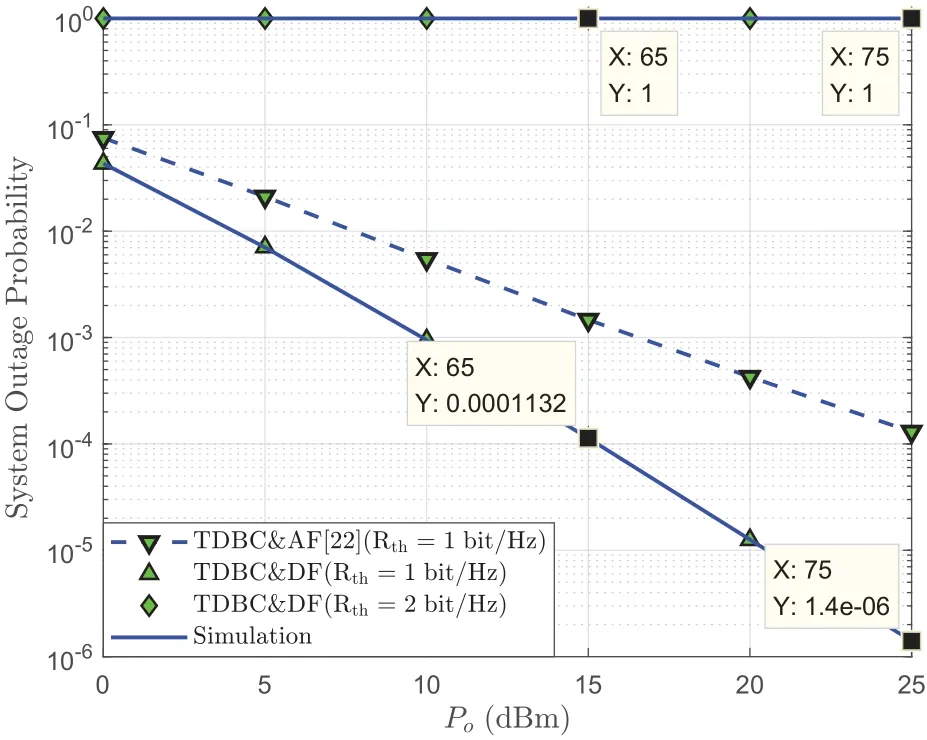
Figure 7.The derived diversity gain d vs. the transmit power of each terminal Po,in comparison with simulation results,where kave=0.1 and{ma,mb,md}={2,1,1}.

Figure 8 depicts the system outage probability versus the PS ratioβ.As presented in this figure,whenβincreases,all curves decrease first and then increases.Such variation trend is owing to the following fact.According to(6),the harvested energy atRgradually increases asβincreases.Meanwhile,the increase ofβalso reduces the portion of the received signal used for ID atR.Whenβincreases from zero to the optimal value,the increase of the transmit power atRdominantly enhance the system outage performance.However,whenβexceeds the optimal value and further increases,it is hard forRto decode information from two terminals,which in turn increases the system outage probability.Additionally,it can be observed that,for the fixedkave,the optimalβincreases as shape parameters of the relaying links increase.This is becauseRneeds fewer portion of the received signal used for ID as the channel quality of the relaying links improves.

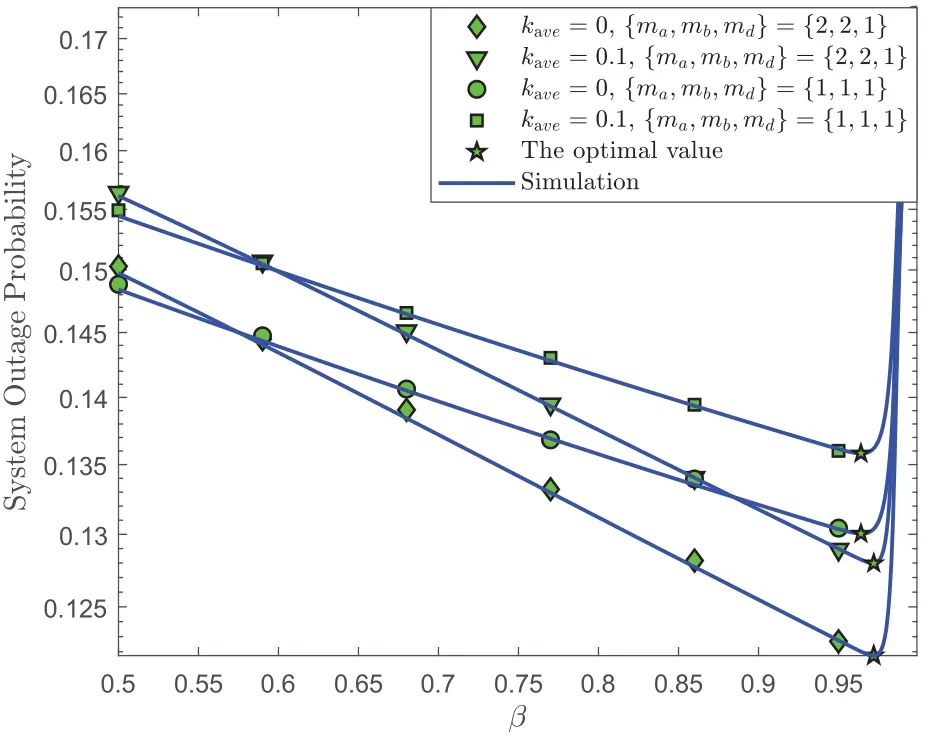
Figure 8.The system outage probability Pout vs. the PS ratio β,where Rth=1 bit/Hz.

Figure 9 shows the system outage probability as a function of the SNDR thresholdγthusing either HIs(kave=0.15) or ideal hardware (kave=0) assumption.From this figure,it can be observed that whenγthis below 22.2,i.e.,the OSC threshold,the system outage performance of our studied network under HIs relies on both the direct and relaying links.Nevertheless,whenγthgoes beyond the OSC threshold,the overall system ceases.These results coincide with the conclusions in Remark 1.Moreover,the impact of HIs is negligible for a low SNDR threshold,but it becomes very severe with increasingγth.Note that,different from the studied network,the SWIPT based AF TWRN suffers from not only the OSC effect but also the RCC effect.More specifically,the RCC prevents the relaying link from carrying out cooperative communication,while the OSC puts the overall system in outage.In addition,we also observe that the relaying links under the AF strategy are more sensitive to HIs than those under the DF strategy.

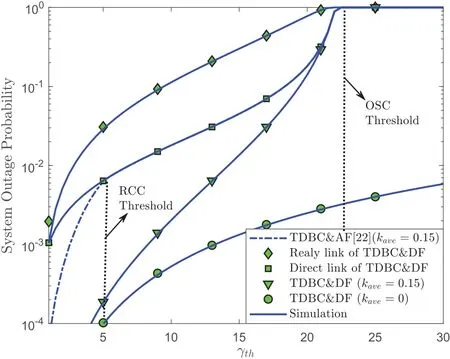
Figure 9.The system outage probability Pout vs. the SNDR threshold γth,where Po=10 dBm and {ma,mb,md}={2,2,1}.

Figure 10 studies the influence of transmit power of each terminalPoon the energy efficiency to get some insights about the utilization of the available energy.Specially,the energy efficiency is defined asEE=,where Poutcan be obtained from(20)[27].From this figure,it can be observed that all curves exist the optimalPomaximizing the energy efficiency.In addition,we can also note that the achievable energy efficiency is low at highPoregion.This is due to the achieved system outage performance is much lower than the consumed energy at high transmit power region.Furthermore,for a fixed transmission rate,the energy efficiency under practical case(kave=0.1)is much lower than that under ideal case(kave=0).This is because the HIs impose an undesirable influence on the system outage performance of our considered network.

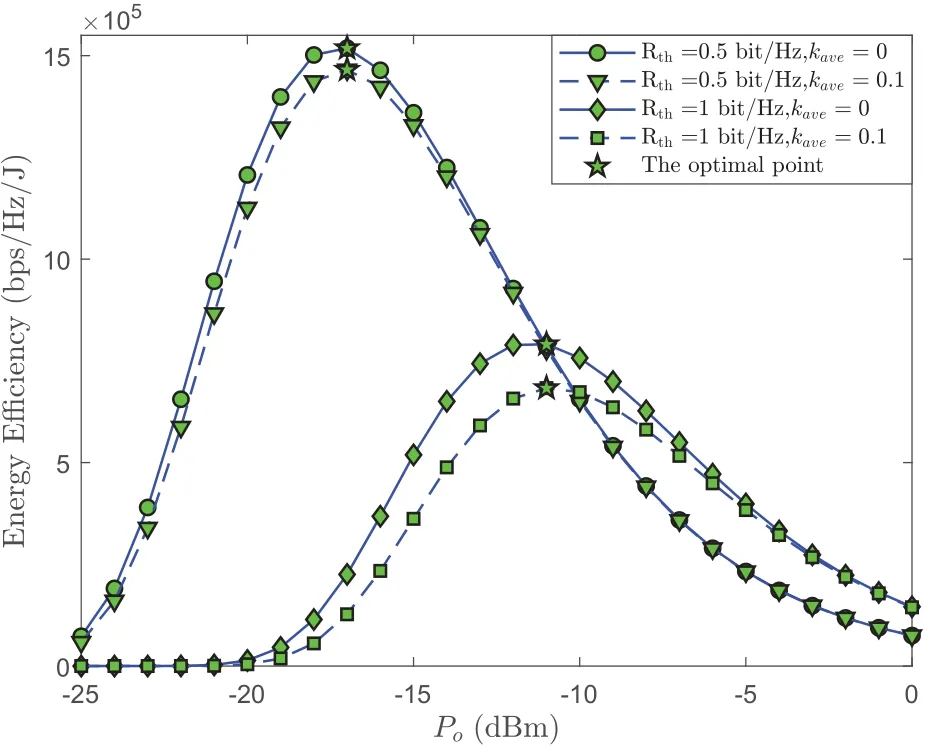
Figure 10.Energy efficiency vs. the transmit power of each terminal Po,where{ma,mb,md}={2,2,1}.

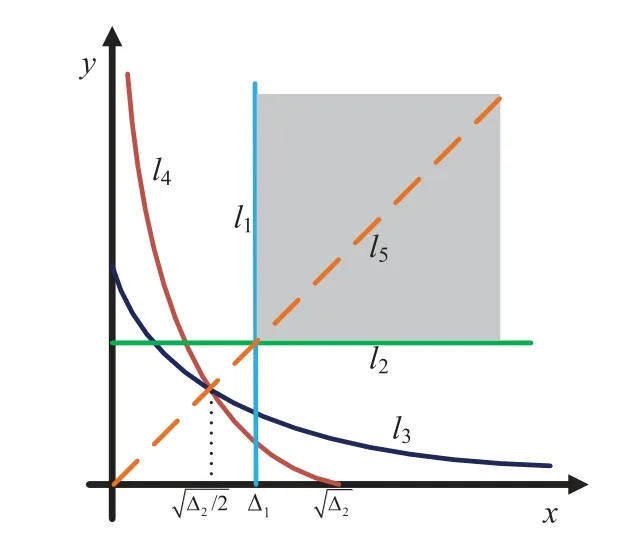
Figure 11.The integral region for P2,where ∆1 ≥.

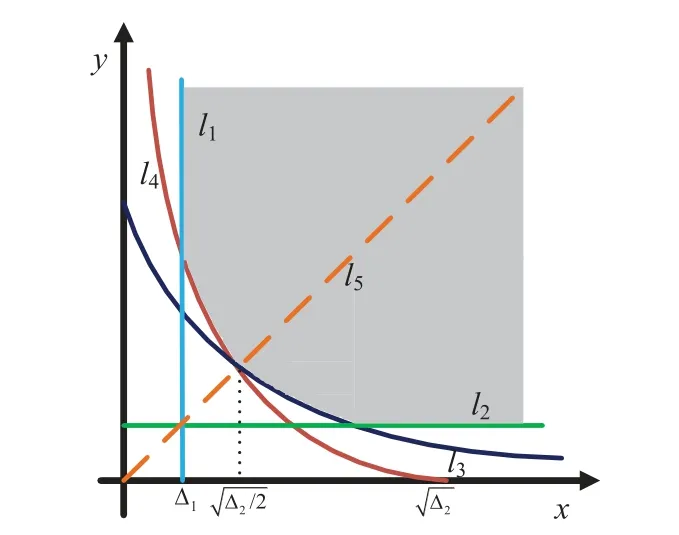
Figure 12.The integral region for P2,where ∆1 <.

V.CONCLUSION

In this work,we have analyzed the system outage probability and the diversity gain of a SWIPT based two-way DF relaying,in which HIs at all transceivers are taken into account.In particular,under i.n.i.d.Nakagami-mfading channels,the closed-form expression for the system outage probability has been obtained.Based the derived expression,we have identified the OSC effect and obtained the achievable diversity gain of our studied network.Our analytical results have revealed the following fact,i.e.,when transmission rate goes beyond the OSC threshold,the overall system is in outage and the diversity gain is zero;otherwise,both the direct and relaying links contribute to enhancing the system outage performance and the resulting diversity gain is the sum of the shape parameter of the direct link and the smaller shape parameter of the terminal-to-relay links,viz.,d=md+min(ma,mb).In addition,numerical results have provided some insights about the effect of multifarious parameters on system outage performance as well as the performance difference between DF and AF strategies.Based on the results,we have provided guideline on how terminals use energy to balance the energy utilization and spectral utilization.

APPENDIX

A The Theoretical Analysis for P1

In order to obtain the closed-form expression for P1,we divide into the following two cases in terms of the range ofγth.

wheremdandare the shape and scale parameters of the gamma random variableZrespectively.According to [[28],eq.(3.381.1)] and [[28],eq.(8.352.6)],we can solve the integration of (A.1),and then obtain the closed-form expression foras given in(16).

B The Theoretical Analysis for P2

Based on the above analysis of P1,we can also derive the closed-form expression for P2in terms of the following two cases.

Case 3.Whenγth≥issatisfied,alltheinequalitiesofP2arenevertrue.Therefore,thecorresponding probabilityisequaltozero,i.e.,P2=1.

Case 4.Whenγth∆1,Y>∆1,X>-Y+∆2/Y,Y>-X+∆2/X},where ∆1=and ∆2=.Obviously,there is the high correlation among the inequalities in P2,which is the main obstacle in deriving P2.Assume thatX=xandY=y.From the expression of P2in(14),the integral region of P2is bounded by four curves,which arel1:x=∆1,l2:y=∆1,l3:x=-y+∆2/yandl4:y=-x+∆2/x.After straightforward mathematical manipulations for the above four curves,we can obtain several conclusions as follows:

1)curvesl3(y)andl4(x)are the monotonically decreasing functions with respect ofyandxrespectively,wherex,y∈(0,+∞).

According to[29,3.381.3],Ξ1can be calculated as

C The Theoretical Analysis for the Diversity Gain

According to(20),the diversity gain can be calculated respectively in the two cases as follows.

Similar to the derivation of Ξ5,we can obtain Ξ6=-min(ma,mb).

Based on the above discussions,the diversity gain can be obtained as(22).

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China under Grant 62201451,in part by the Young Talent fund of University Association for Science and Technology in Shaanxi under Grant 20210121,in part by the Shaanxi provincial special fund for Technological innovation guidance(2022CGBX-29),in part by BUPT Excellent Ph.D.Students Foundation under Grant CX2022106.

NOTES

1Compared with MABC,TDBC enjoys a lower operational complexity at the relay node and utilizes the direct link[13,14],hence we adopt the TDBC instead of the MABC.

2Note that[23]focused on the T2T outage probability,which counts the outage event of one terminal only and is different from the system outage probability considered in our work.

3In order to avoid complicated algebraic operations,integer shape parameters of Nakagami-mfading are assumed in this work [17,23,24].Please note that relaxing this assumption can make the analysis more general,which will be studied in our future work.

4Actually,the total transmit power ofSiequals,which is greater than the power ofxi.According to the HIs level region specified by the 3GPP LTE [17],viz.,ki∈[0.08,0.175],i={1,2},should hold to always meet the transmit power constraint≤PSi,max,wherePSi,maxdenotes the maximum transmit power ofSi.

5Given that the vast majority of the receiver distortion noises are generated in the down-conversion process,we ignore the distortion noise induced by the receiving process at the antenna for analytical tractability [22,24].

6According to the definition of outage event,Poutcan also be expressed as Pout=where Λ1and Λ2denote the T2T outage probabilities atSaandSbrespectively,and Λ3denotes the probability that bothSaandSbare in outage.Since there is a high correlation between two T2T links,viz.,Sa→SbandSb→Salinks,Λ3≠Pr{γa<γth}Pr{γb<γth},which means that the system outage probability cannot be directly derived from T2T outage probabilities and the theoretical analysis for the system outage probability is more challenging.

7Owing to the sufficient accuracy even with very few terms,we adopt the Gaussian-Chebyshev quadrature instead of other approximation approaches.Note that such a method has been widely adopted in existing works[7,13,14,30,31].