A Deep Reinforcement Learning-Based Power Control Scheme for the 5G Wireless Systems

Renjie Liang ,Haiyang Lyu ,Jiancun Fan,*

1 School of Electronic and Information Engineering,Xi’an Jiaotong University,Xi’an,Shaanxi 710049,China

2 School of Cyber Science and Engineering,Xi’an Jiaotong University,Xi’an,Shaanxi 710049,China

*The corresponding author,email: fanjc0114@gmail.com

Abstract: In the fifth generation (5G) wireless system,a closed-loop power control (CLPC) scheme based on deep Q learning network (DQN) is introduced to intelligently adjust the transmit power of the base station (BS),which can improve the user equipment (UE) received signal to interference plus noise ratio(SINR)to a target threshold range.However,the selected power control(PC)action in DQN is not accurately matched the fluctuations of the wireless environment.Since the experience replay characteristic of the conventional DQN scheme leads to a possibility of insufficient training in the target deep neural network(DNN).As a result,the Q-value of the sub-optimal PC action exceed the optimal one.To solve this problem,we propose the improved DQN scheme.In the proposed scheme,we add an additional DNN to the conventional DQN,and set a shorter training interval to speed up the training of the DNN in order to fully train it.Finally,the proposed scheme can ensure that the Q value of the optimal action remains maximum.After multiple episodes of training,the proposed scheme can generate more accurate PC actions to match the fluctuations of the wireless environment.As a result,the UE received SINR can achieve the target threshold range faster and keep more stable.The simulation results prove that the proposed scheme outperforms the conventional schemes.

Keywords: reinforcement learning;closed-loop power control (CLPC);signal-to-interference-plusnoise ratio(SINR)

I.INTRODUCTION

In the wireless downlink channel of the third generation (3G) system,a conventional closed-loop power control (CCLPC) [1] is employed to resist the fluctuations of the wireless channel.In the CCLPC scheme,the user equipment (UE) first compares the gap between the UE received signal-to-interferenceplus-noise ratio(SINR)and the target SINR threshold.Then,based on the SINR gap,the UE sends a message named transmit power control (TPC) to the base station (BS) to let the BS adjust the transmit power at a fixed step.The above process repeats until the UE receive SINR reaches the target SINR threshold and stops.

The closed-loop power control (CLPC) scheme is also proposed for the wireless uplink channel in the fifth generation (5G) wireless system.On the other hands,a fixed power allocation (FPA) scheme [2] is proposed in the wireless downlink channel of the 5G system.In the FPA scheme,each radio block(RBs)is allocated a fixed power,and the total power of all RBs cannot exceed the BS’s transmit power.As a result,the FPA scheme cannot compensate for the fluctuations of the wireless environment rapidly and adaptively.Therefore,how to effectively compensate for the unexpected wireless environment fluctuations is a problem.A feasible solution is using the CLPC method.In the CLPC method,the BS reversely adjusts its transmit power according to the fluctuations of the wireless environment to compensate for it,thereby alleviating the degradation of the UE received SINR.

There are lots of works investigating on the topic of the CLPC in the 5G system [3–5].Meanwhile,there are also lots of works investigating on RL-based schemes to improve the performance of the 5G system [6–12].In [11],the DQN-based scheme is proposed to control transmission power dynamically to improve non-line-of-sight (NLOS) transmission performance of the 5G wireless communication systems.In [12],the DQN scheme is proposed to improve the system performance of non-cooperative cognitive radio networks.However,there are much fewer works using the reinforcement learning(RL)-based schemes to investigate the topic of CLPC [13,14].In [13],the Q-learning scheme is proposed to compensate for the fluctuations of the wireless environment in indoor scenarios in the 5G system.Although the Q-learning scheme is simple to implement and can quickly converge,it has a limited improvement in system performance.In[14],a power control and interference cancellation (PCIC) scheme based on the DQN is proposed to improve the downlink transmission performance of the millimeter wave system.

In the DQN scheme,the BS first randomly adjusts its transmit power(also named as PC action)to interact with the fluctuations in the wireless environment.If the PC action that matches the fluctuations of the wireless environment is found,it is stored in the Deep Neural Network(DNN)[15].After multiple training,the DNN’s prediction is used to select matching PC actions to resist fluctuations in the wireless environment.However,there is a problem that the selected PC action is not accurate enough in the DQN scheme.Due to the characteristics of experience playback[16],the target DNN is trained once per episode in the conventional DQN scheme,instead of each dual-slot whose duration is shorter.Such a relatively long training interval will lead to insufficient DNN training,resulting in the Q value of the sub-optimal PC actions exceeding the optimal PC actions.As a result,the selected maximum Q-value PC action is always not optimal,but sub-optimal.The sub-optimal PC actions will cause the BS’s transmit power to not accurately match the fluctuations of the wireless environment.If the BS’s transmit power is too large,the BS will consume too much energy and interfere with the signals of other BSs.On the contrary,if it is too small,the BS’s transmit power will not be sufficient to compensate for fluctuations in the wireless environment,which will cause the UE received SINR cannot reach the target SINR threshold range.

In this paper,we propose the improved DQN scheme to search for more accurate PC actions to better compensate for fluctuations in the wireless environment.Compared with training the target DNN once for each episode in the conventional DQN scheme[17],we add an additional DNN and train it once for each dual time-slot in the improved DQN scheme.Due to the shorter training interval,the DNN converges more sufficiently,which can ensure that the Q value of the sub-optimal PC action will not exceed the optimal PC action.As a result,it will generate more accurate PC actions in the improved DQN scheme compared with the conventional DQN.Finally,the adjustment of the BS’s transmit power can enable the UE’s received SINR to reach the target SINR threshold range faster and remain more stable.

The rest of this paper is organized as follows.In Section II,we introduce the system model and the channel model.Section III outlines the problem formulation.In Section IV,we propose the improved DQN scheme.In Section V,we simulate the proposed scheme compared with the conventional schemes,and prove the advantage of our scheme.We conclude the paper in Section VI.

II.SYSTEM MODEL AND CHANNEL MODEL

In this section,we introduce the radio environment,the system model,and the channel model.

2.1 Radio Environment

As shown in Figure 1,we assume that there is a time division duplexing (TDD) wireless system deployed in an indoor environment.In this system,there areNomni-directional antennas BSs.Meanwhile,there is a single antenna UE located at the coverage edge of the BS0.

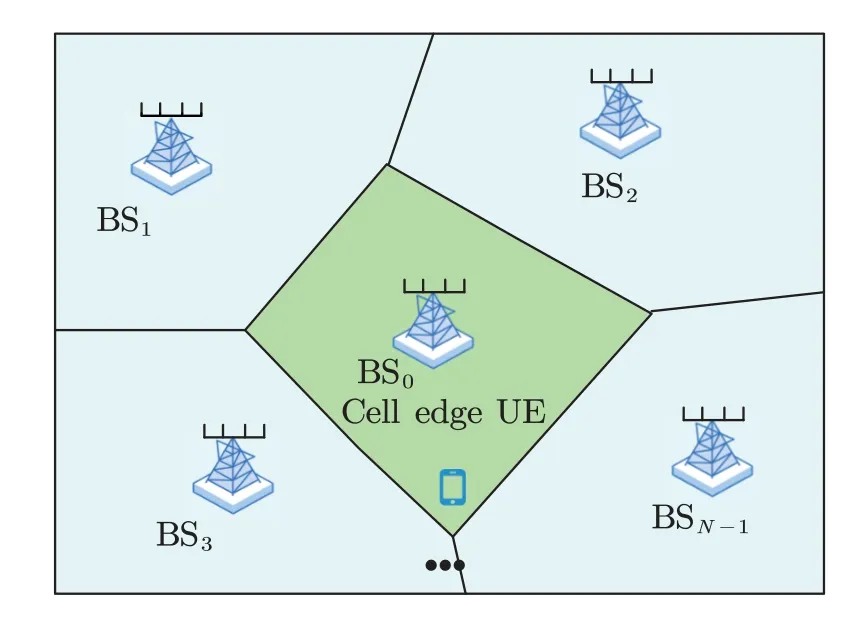
Figure 1.The radio environment.

2.2 System Model

By considering the radio environment in Section 2.1,the UE received signal can be expressed as

wherehi[t] denotes the channel connecting the BSiand the UE at arbitrary timet,xi[t]denotes the transmit signals from BSito UE at arbitrary timet,andN0denotes the UE received additive complex Gaussian noise(AWGN)with zero-mean and varianceσ2at arbitrary timet.The first term in Eq.(1)denotes the UE received signal from the BS0which is the serving cell,while the second term denotes the UE received inter cell interference(ICI)from the neighboring BSs.

2.3 Channel Model

For the channel model,we need to consider both largescale fading such as shadow fading and small-scale fading such as scattering and reflection.

To consider the small-scale fading,we can employ the Rician fading channel model[18,19]which can be expressed as

whereκi[t]denotes the path loss of the BSi-UE channel at arbitrary discrete timet,θdenotes the angle of arrival at the line-of-sight (LOS) path,follows the complex Gaussian distribution with zero mean and unit variance,andKdenotes the Rician K-factor of

By considering the shadow fading,the path loss in dB can be expressed as

whereκi,dB[t]denotes the path loss in dB of the BSi-UE channel at arbitrary timet,κr,dBdenotes the path loss in dB of the reference distancedr,Mdenotes the path loss exponent(PLE),didenotes the distance from the BSiand the UE,andξdenotes the Gaussdistributed random variable with zero mean and variance,which is the shadow factor(SF)[20]related to the shadow fading.

Based on the channel model in Eq.(2),the UE received power from the BSiat arbitrary timetcan be expressed as

wherePBS,i[t] denotes the BSi’s transmit power at timet.Therefore,the UE received SINR at arbitrary timetcan be expressed as

Substituting Eq.(2),Eq.(3)and Eq.(4)into Eq.(5),the UE received SINR can be convert to

From Eq.(6),we can find that the UE received SINRγ[t] is time-varying.Since that the distance between the UE and the BS can be changing,the large-scale fading and the small-scale fading is timevarying.Therefore,the random fluctuations of the wireless environment including large-scale fading and small-scale fading will significantly affect the UE received SINRγ[t].If the UE received SINR deteriorates,we can raise the BS0’s transmit power to compensate for it.On the contrary,if the UE received SINR restores,we can reduce the BS0’s transmit power to reduce the BS0’s power consumption.Therefore,we can add a variable transmit power offset∆PBS[t]at the fixed transmit power of the BSPBS,baseas

Substituting Eq.(7)into Eq.(6),we can obtain

According to Eq.(8),it is feasible to adjust the BS’s transmit power ∆PBS[t] to compensate for the fluctuations of the wireless environment.However,how to intelligently adjust the BS’s transmit power so that the UE received SINR can rapidly achieve the target threshold range and keep stable within the target SINR threshold range is a problem worthy of study.

III.PROBLEM FORMULATION

As discussed in Section II,our target is to accurately compensate for the random fluctuations of the wireless environment by intelligently adjusting the BS’s transmit power,thereby increasing the cell edge UE’s received SINR within the target threshold range.To achieve the target,we need to model it as a Markov decision process(MDP)and solve it.

Before discussing this scheme,we first introduce some definitions in the RL theory,including agent,environment,state,reward,and action.in the RL theory,an agent is an entity that implements intelligent behaviors.In this paper,we define the BS as an agent.The environment is the object that the agent interacts with.In this paper,we define the wireless environment as the environment in the RL theory.The state is the measure of the environment’s property in the RL theory.In this paper,the state at arbitrary discrete timetis the cell edge UE received SINRγedge,UE[t] which can be further abbreviated asγ[t].Simultaneously,we suppose there is a set named state spaceSwithMdiscrete elements,which can be expressed as

wherei=1,2,...,M.We assume that for arbitrary discrete timet,theγ[t] can only select an element from the state spaceS.In theory,the UE received SINRγ[t] is a continuous value with infinite resolution.However,in actual deployment,the resolution of the UE received SINRγ[t]’s value is finite.Therefore,we define a set of discrete values to describe it.As discussed in Section II,we aim to let the edge UE received SINRγ[t] reach and stay between the target SINR threshold range[γLB,γUB],which can be expressed as

In order to achieve and stay stay between the target SINR threshold range[γLB,γUB],we design an instant reward based on the RL theory.If the threshold range[γLB,γUB] is not achieved,the agent will generate a negative reward,and if the threshold range[γLB,γUB]is achieved,the agent will generate positive reward.Therefore,the reward function can be expressed as

wherer-denotes the negative reward,r+denotes the positive reward.In order to improve the UE received SINR,as discussed in Section II,we can add a PC action to the fixed transmit power of the BSPBS,baseto compensate for the fluctuations of the wireless environment.Based on this,we can define actiona[t] to denote the PC action as

Simultaneously,we suppose there is a set named state spaceAwithNdiscrete elements,which can be expressed as

wherei=1,2,...,N.We assume that for arbitrary discrete timet,thea[t]can only select a element from the state spaceA.

In order to describe the CLPC process,except for introducing the above RL related definitions,we also design a dual time-slot structure in the TDD mode.As shown in Figure 2,one single dual time-slot contains one uplink time-slot and one downlink time-slot.Meanwhile,theKconsecutive dual time-slots are defined as one episode.

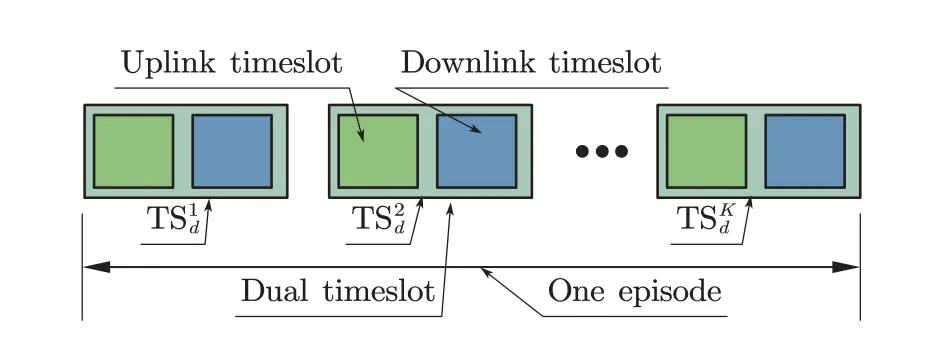
Figure 2.The dual time-slot structure in one episode.

After introducing the above definitions,we can describe the CLPC process.As shown in Figure 2,in each single episode of the CLPC process,the UE sends the report of the downlink SINRγ[t]to BS in the uplink time-slot of dual time-slott.After receiving the report,in the subsequent downlink time-slot,the BS adjusts its transmit power by selecting a PC actiona[t] and calculates the instant rewardR[t] according to Eq.(11).This is a closed loop interaction process between the UE and the BS,which can be named as the single interaction loop as shown in Figure 3.

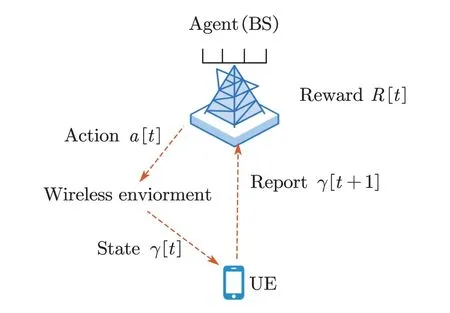
Figure 3.The single interaction loop.

We can iteratively repeat the single interaction loop until the maximum number of repetitionsKis reached as shown in Figure 4.Meanwhile,we define the dual time-slot that the UE received SINR first time to achieve the target SINR threshold range as the initial achieving dual time-slotTSd,IAas shown in Figure 4.

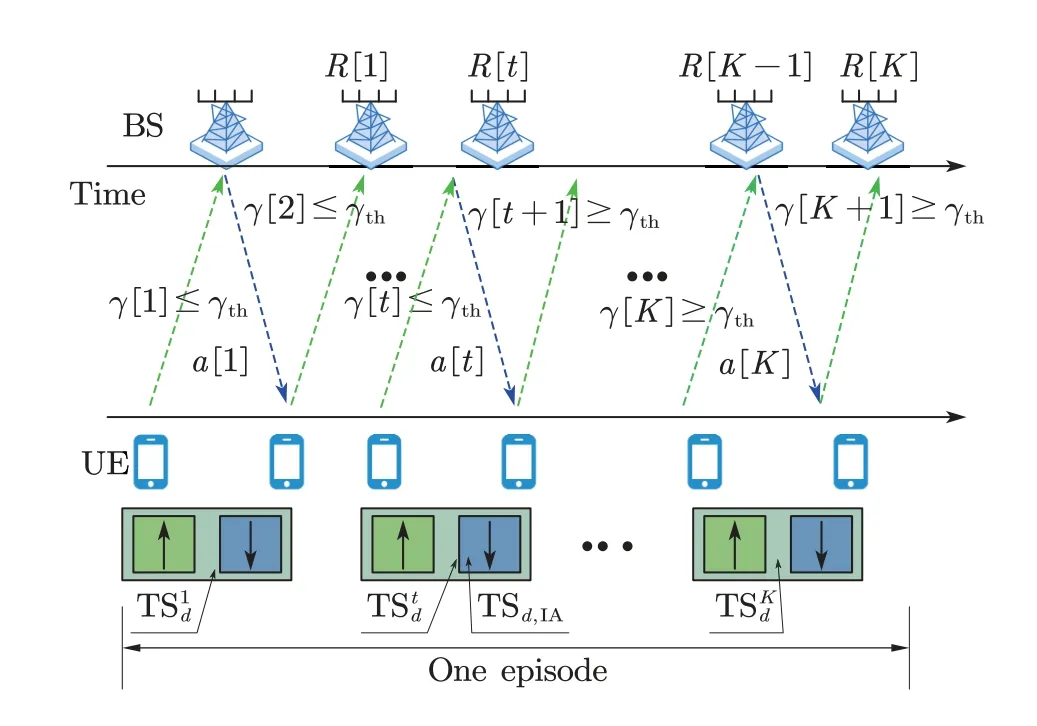
Figure 4.The K interaction loops in one episode.

Base on above analysis,this whole episode can be modeled as a Markov decision process(MDP)[17]as

From the MDP in Eq.(14),we can see that in each dual time-slot of the CLPC process,if the BS randomly tries different PC actions instead of intelligently selecting a accurate PC action,it will be difficult to achieve and stay within the target threshold range [γLB,γUB] for the UE received SINR.Therefore,we need to find an optimal strategy for intelligently selecting a accurate PC action to achieve the target threshold range rapidly and stay stable within the range.However,how to find the optimal strategy is a difficult problem to solve.The schemes in the RL theory can be employed to find an optimal strategy for the MDP [21].In the next section,we will introduce the improved DQN scheme to solve this problem.

IV.PROPOSED SCHEME

In this section,we first analyze the problem of inaccurate PC action selection in conventional DQN scheme.Then,we propose the improved DQN scheme to solve this problem.

In order to intelligently select accurate PC actions to compensate for the fluctuations of the wireless environment,we design a long-term rewardsRtotal[t] in the RL theory to measure how accurately a PC action matches the fluctuations of the wireless environment as

whereRtotaldenotes long-term reward,which can also be called value.α∈[0,1] denotes the discount factor for the long-term reward.However,the long-term rewardRtotalis a random variable.Therefore,we employ its expectationQ(γ[t],a[t])instead of it to measure whether a PC action more accurately matches the fluctuations of the wireless environment.TheQ(γ[t],a[t]) of the current stateγ[t] with actiona[t]can be expressed as follows:

where E(·)denotes the expectation of a random variable.Substituting Eq.(15)into Eq.(16),according to the Bellman equation[21],we can obtain

Since Eq.(18)cannot be deployed in the actual scenarios.An iterative solution is employed to solve Eq.(18),which can be expressed as

where theβdenotes the learning rate,which is a hyper-parameter,Q′(γ[t],a[t])denotes the Q value of the next iteration.If the condition

is met,it means that the scheme has converged,where theϵ>0 denotes the threshold which is a very small value.In this way,we can provide a Q table [22]whose input is a state-action pair and the outputs are their Q values.This scheme is named as Q-learning[23] scheme in the RL theory.If the DNNs are employed to imitate the Q-table,and two characteristics of experience replay and fixed Q target are employed,it is named as the DQN[16]scheme.In DQN,there are two DNNs,named target DNN and evaluation DNN [24].After the DQN’s DNNs are fully trained,the loss function

can be minimized,whereL(w)denotes the loss function,wandw′denotes the weights of target DNN and evaluation DNN of the DQN,respectively.

However,there is a problem with the conventional DQN scheme.Due to the characteristic of experience replay in the DQN scheme,the weights of the target DNN are trained once per episode.The training interval is relatively long,resulting in the weights of the target DNN not being updated in time.Therefore,the Q value of the sub-optimal action can easily exceed the Q value of the optimal PC action.As a result,the sub-optimal action corresponding with the largest Q value is selected in the DQN scheme.It will cause the BS’s transmit power to not accurately match the fluctuations of the wireless environment.Therefore,there is room for further improvement.

To solve this problem,we can shorten the training interval of the DNN to update its weights faster.To meet the above demand,we propose the improved DQN scheme.In the improved DQN scheme,we add an additional DNN to the conventional DQN scheme as shown in Figure 5.The additional DNN imitates the Q-table[21]with input the statesγ[t]and actionsa[t]to generate all possible Q values of the state-action pairs.

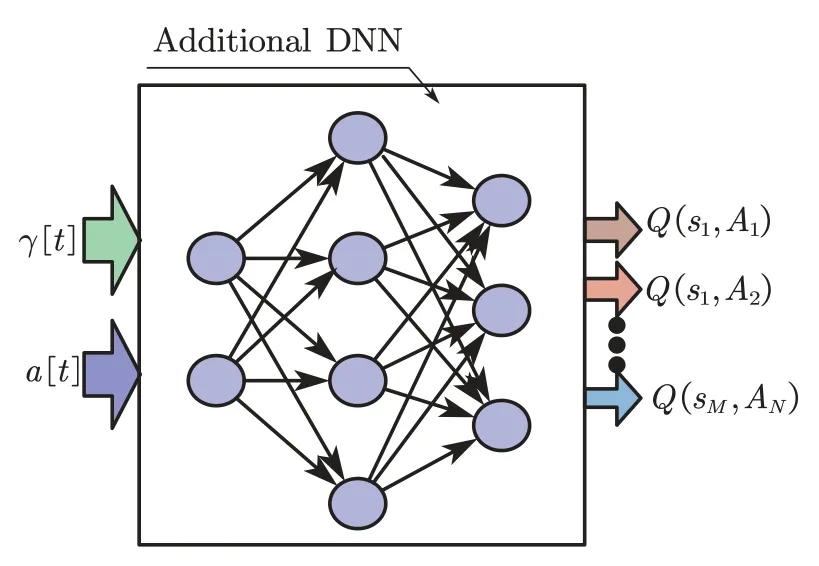
Figure 5.The additional DNN’s structure.

We first train the additional DNN to update its weights in each dual time-slot,instead of training once in each episode of the conventional DQN.Therefore,the DNN is trained more sufficiently,which can ensure that the Q value of the sub-optimal action does not exceed the Q value of the optimal PC action.Then,the sufficiently trained additional DNN generates Q values for all PC actions.Among them,the PC action with the largest Q value is the optimal PC action rather than the sub-optimal PC action.Therefore,the improved DQN can generate more accurate PC actions than the conventional DQN.Finally,the PC action with the largest Q value is selected as the input of the target DNN,which can be expressed as

wherew′′denotes the weights of the additional DNN.Finally,as shown in Figure 6,we train the weights of all DNNs in the improved DQN to minimize the loss function

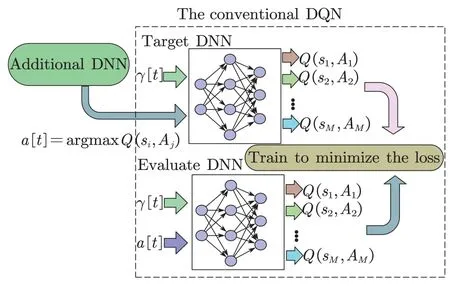
Figure 6.The improved DQN structure.

Therefore,the more accurate PC actions can be generated in the improved DQN scheme compared with the conventional DQN scheme.

Based on the above analysis,the improved DQN scheme can be summarized in Alg.1.

V.SIMULATION RESULTS

In this section,we evaluate the performance of the proposed scheme through several simulation results.In this section,we use several simulation results to evaluate the performance of the proposed scheme.

For the radio environment,we assume that the frequency of the wireless system is 3.4 GHz (n77 band for 5G system).As shown in Figure 7,there are 5 BSs,and the UE is at the coverage edge of the BS0.The distance between the neighbor BSsdBS=200 m.The distance between the BS0and arbitrary neighbor=140 m.The distance between the BS0and the UEdBS0-UE=70 m.All the BSs’ fix transmit powerPBS,baseare 40 dBm,and theof the UE received AWGN is -95 dB.The target SINR threshold range [γLB,γUB] is [4,5] dB.For the path loss model in Eq.(3) of the wireless system [25],the reference distancedris 1 m,the path loss of the reference distanceκr,dBis 43.3 dBm,the path loss exponent(PLE)Mis 2 for the LOS scenario,and the=3 dB.For the Rician fading channel model,the Rician K-factorK=3.

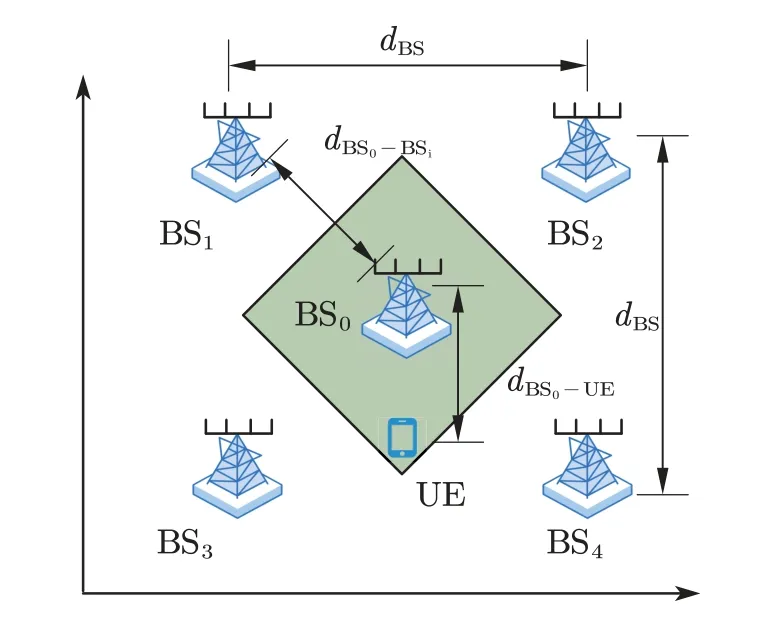
Figure 7.The simulation setup.

Table 1.The simulation parameters of the improved DQN.

For the simulation parameters of the improved DQN in the proposed scheme,the actionaiin the action spaceAis quantized in the range of [-20dB,20dB],and the quantization resolution is 0.1 dB.All PC actionsa[t] are selected fromA.Similarly,the statesiin the state spaceSis quantized in the range of[-10dB,10dB],and the quantization resolution is 0.1 dB.All the UE received SINRγ[t]are selected fromS.The positive rewardr+and negative rewardr-in the reward function Eq.(11) is 100 and -1,respectively.In the improved DQN,the number of hidden layers of the target DNN,the evaluate DNN and the additional DNN is the same,but the simulation parameters of neural units in each layer are different.The detailed simulation parameters of the improved DQN are summarized in Table.1.

For the simulation comparison,we consider the following schemes: 1) The proposed scheme in Section IV;2) The FPA scheme in [13];3) The conventional DQN scheme in[14];4)The CCLPC scheme in[1].

We train the DNN in the improved DQN for 2000 episodes,which contains 40 dual time-slots in each episode.We calculate the average value of all rewards in each episode and define it as the average reward per episode.The average reward per episode of thei-th episode is expressed as

whereR[t] denotes the reward of thet-th dual timeslot in thei-th episode.Ifis closer tor+,it means that the proportion of dual-slot withr+rewards in an episode is closer to 100%.In other words,the closeris tor+,the more sufficiently trained the DNN is.AfterTepisodes of iterative training,we can judge whether the DNN is sufficiently trained according to the average reward per episode.

As shown in Figure 8,we plot the average reward per episode versus the episodes.From Figure 8,we can find that the average reward per episodeincreases and gradually gets closer to ther+reward as the training episodes increase.Finally,the DNN in the proposed scheme has been sufficiently trained in 2000 episodes.

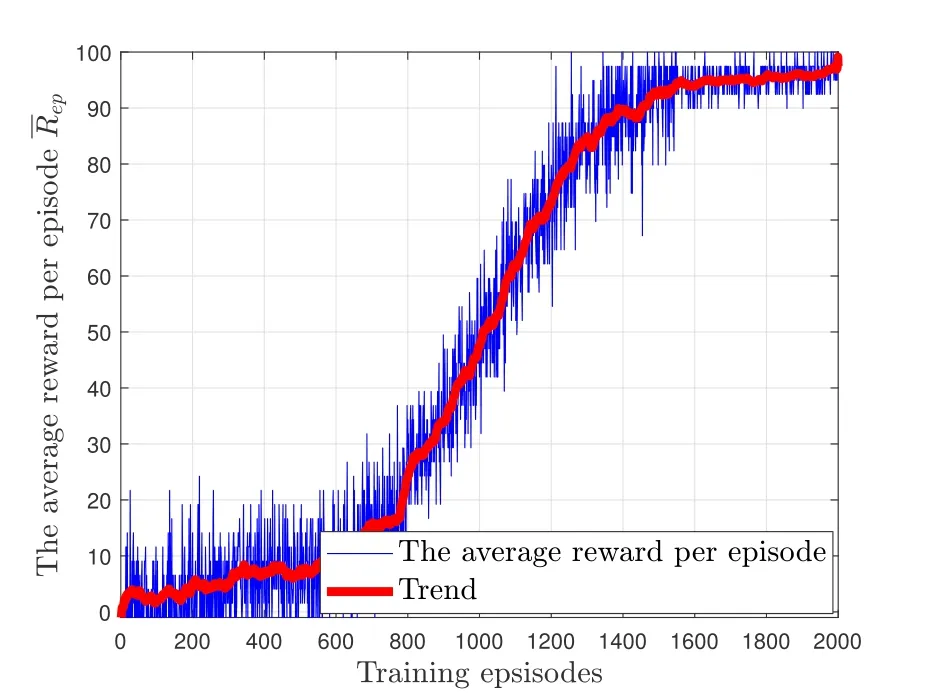
Figure 8.The average reward per episode versus training episodes.

As shown in Figure 9,we plot the UE received SINR versus the dual time-slots in one episode.From Figure 9,we can find that if the DNN in proposed scheme is not trained,the UE received SINR cannot achieve the target SINR threshold range [γLB,γUB]=[4,5]dB.After sufficient training,the UE received SINR can reach the target threshold range faster and remain more stable within the threshold range in the improved DQN scheme than the conventional DQN schemes.

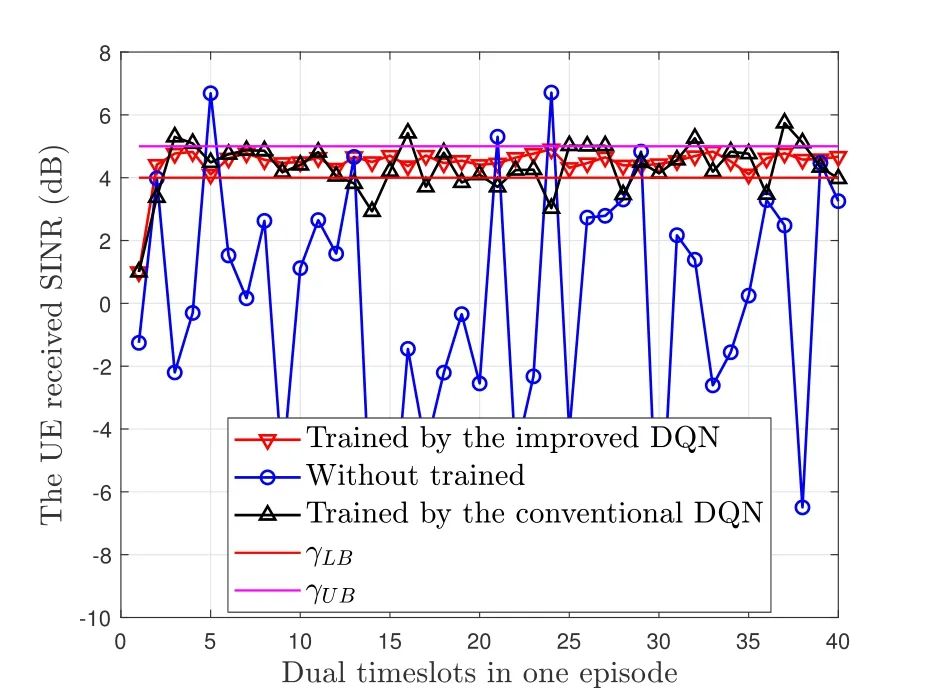
Figure 9.The training of various schemes in one episode.

Based on the sufficiently training of the DNN in the proposed scheme,we further simulate 1000 episodes.scheme mainly varies in the target threshold range of[4dB,5dB].In other words,the UE received SINR in the proposed scheme is more stable compared with other schemes.The reason is that the improved DQN can provide more accurate PC actions than the remaining schemes to compensate for the fluctuations of the wireless channel.Meanwhile,we can find that compared with the remaining schemes,the average UE received SINR in the improved DQN is higher.Since in the improved DQN,the UE received SINR can achieve the target threshold range faster than the remaining schemes,as shown in Figure 10.In order to measure how rapidly the UE received SINR reaches the target threshold range,we define the dual time-slot when the UE received SINR for the first time to achieve the target SINR threshold range as the initial achieving dual time-slot TSd,IAas shown in Figure 4.

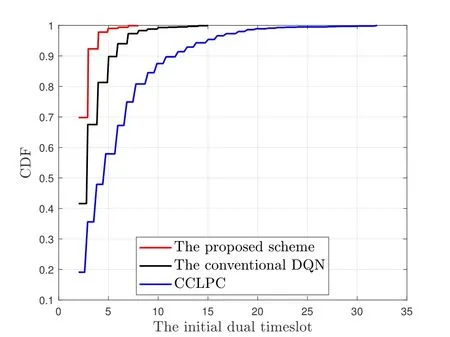
Figure 10.The CDF of the initial dual time-slot.

As shown in Figure 10,we plot the cumulative distribution function (CDF) of the initial achieving dual time-slot TSd,IAunder various schemes.We can find that it requires less dual time-slots to achieve the target threshold range in the proposed scheme than the remaining schemes.In other words,the UE received SINR in the proposed scheme can reach the target threshold range faster compared with the remaining schemes.

As shown in Figure 11,we plot the CDF of the UE received SINR under various schemes.From Figure 11,we can find that compared with the remaining schemes,the UE received SINR in the proposed

Figure 11.The CDF of the UE received SINR.

VI.CONCLUSION

In this paper,we aimed to intelligently and rapidly compensate for the random fluctuations of the wireless environment by adjusting the transmit power of the BS.However,since the PC actions that the conventional DQN provides are not accurate enough to match the fluctuations of the wireless environment.Therefore,we proposed the improved DQN scheme,which adds an additional DNN to the conventional DQN scheme to provide more accurate PC actions that match the fluctuations of the wireless environment.The simulation results showed that the proposed scheme outperforms the conventional schemes.