Differential Scheme for Reconfigurable Intelligent Surface-Based Spatial Modulation System

Han Hai ,Si Wei ,Xueqin Jiang,* ,Yuyang Peng ,Mohsen Guizani

1 College of Information and Science Technology,Donghua University,Shanghai 201620,China

2 School of Computer Science and Engineering,Macau University of Science and Technology,Macau 999078,China

3 Mohammad Bin Zayed University of Artificial Intelligence,Abu Dhabi,UAE

*The corresponding author,email: xqjiang@dhu.edu.cn

Abstract: In this paper,a differential scheme is proposed for reconfigurable intelligent surface (RIS) assisted spatial modulation,which is referred to as RISDSM,to eliminate the need for channel state information(CSI)at the receiver.The proposed scheme is an improvement over the current differential modulation scheme used in RIS-based systems,as it avoids the high-order matrix calculation and improves the spectral efficiency.A mathematical framework is developed to determine the theoretical average bit error probability (ABEP) of the system using RIS-DSM.The detection complexity of the proposed RIS-DSM scheme is extremely low through the simplification.Finally,simulations results demonstrate that the proposed RIS-DSM scheme can deliver satisfactory error performance even in low signal-to-noise ratio environments.

Keywords: reconfigurable intelligent surface (RIS);differential scheme;spatial modulation (SM);detection complexity

I.INTRODUCTION

In recent years,the fifth-generation (5G) wireless communication technology has grown in popularity as a research area.To meet 5G standard,massive multiple-input multiple-output(MIMO)technology is proposed and becomes one of the key technologies of 5G,which significantly increases the capacity of the system [1].As 5G communication networks become increasingly commercialized,researchers have started exploring the potential emerging technologies of 6G networks to accelerate data transfer and improve service quality [2,3].These technologies include new non-orthogonal multiple access (NOMA) [4],visible light communication,spatial modulation (SM),and terahertz communications,among others.However,the practical use of those technologies leads to high hardware prices and power consumption.

Due to its passiveness,affordability,and low power consumption,the reconfigurable intelligent surface(RIS) technology gains the interest of both industry and academia.[5].On the one hand,the RIS of artificial electromagnetic materials is a smart device that manages the propagation environment to enhance the receiver signal quality [6].On the other hand,RIS can use itself as a point of access to generate virtual phase shift keying(PSK)symbols for transmission[7].However,the spectral efficiency is limited in conventional RIS system.

Index modulation (IM) technology [8] is proposed as a promising means to improve spectral efficiency and energy efficiency,which selects different indices to transfer additional data[9].Incorporating IM based on the slicing of the power level into NOMA,a outstanding technique that can enable higher spectral efficiency and better user fairness is proposed for the 6G multiple access [10].Introducing IM into RIS-aided communications is a clever manner to improve the spectral efficiency [11].Several RIS-based IM techniques are proposed to provide high data rates at even low signal-to-noise ratio (SNR),such as the RIS assisted SM(RIS-SM),receive SM(RIS-RSM),quadrature SM(RIS-QSM),generalized SM(RIS-GSM)and space shift keying (RIS-SSK) schemes [12].In [13],a reflecting modulation(RM)scheme is proposed,allowing data to be transmitted through the reflection of patterns and signals.RIS-aided receive quadrature reflecting modulation(RIS-RQRM)is proposed in[14]for the first time,where the RIS elements are partitioned into two equal subsets to independently implement SM.In [15],a novel reflection pattern modulation (RPM) scheme has been proposed for passive beamforming and data transmission.In [16],a RIS grouping-based index modulation(RGB-IM) approach is proposed.It segments the RIS into a fixed number of elements,which are organized into groupsurfaces.The data is then modulated to a spatial symbol to activate the index of the corresponding groupsurface.In order to perform coherent detection,the receiver must have full knowledge of the channel state information(CSI),which adds extra complexity to the detection process at the receiver.Furthermore,as the passive RIS elements are unable to detect and estimate the CSI,the estimation of the CSI at the RIS is a difficult task[17–19].

As an effective and fantasy method,the differential spatial modulation(DSM)scheme[20,21]allows for detection without the need for knowledge of the CSI at the receiver.Consequently,a proposed differential reflecting modulation (DRM) scheme,which applies a conventional differential modulation scheme for RIS based communication system,is capable of functioning without knowledge of CSI at the receiver[22].In the DSM scheme,transmit antenna elements and modulated symbols are mapped into information matrices.In this case,the number of information matrices grows exponentially with the number of transmit antennas,resulting in high detection complexity especially for a large number of transmit antennas.

Against the background,this paper aims to propose a differential scheme for RIS-SM,which separates the detection of antenna index and the detection of modulated symbol so as to reduce the detection complexity.Thus,the contributions of this work are summarized as follows:

1.A differential scheme for the RIS-SM is proposed,which is referred to as RIS-DSM.Unlike the DRM scheme,the incoming data bits of RIS-DSM scheme are respectively mapped into receive antenna index and modulated symbol instead of information matrices,which improves the spectrum efficiency(SE).

2.To suit the proposed RIS-DSM scheme,a mathematical framework is presented,which is able to estimate its theoretical average bit error probability(ABEP).

3.Through the simplification of detection complexity and simulations,it is proved that RIS-DSM scheme can provide a satisfactory bit error probability(BER)performance in low SNR regions and the detection complexity of it is extremely low.

The remainder of the paper is structured as follows.Section II presents the proposed RIS-DSM scheme.Section III presents the theoretical ABEP of the proposed RIS-DSM scheme.The detection complexity of the proposed RIS-DSM scheme is discussed in Section IV.Section V provides simulation results,and the paper is concluded in Section VI.

II.THE PROPOSED RIS-DSM SCHEME:SYSTEM MODEL,TRANSMISSION AND DETECTION

The system model is depicted in Figure 1,it shows the use of RIS as a reflector in a communication scenario with a single transmit antenna at the radio frequency source (S) andNrreceive antennas at the destination(D).The signals generated by S are reflected off the RIS to reach D,despite the obstacles between them.We assume that the RIS is composed ofNsimple and reconfigurable reflector elements,with the phase of each element characterized byϕi(i=1,2,...,N),hiandgl,i.These values correspond to the CSI between the single transmit antenna of the source and thei-th reflector element,and the CSI between thel-th receive antenna of the destination and thei-th reflector element,respectively.Assuming that the channels experience Rayleigh fading,we havehi,gl,i∼CN(0,1).

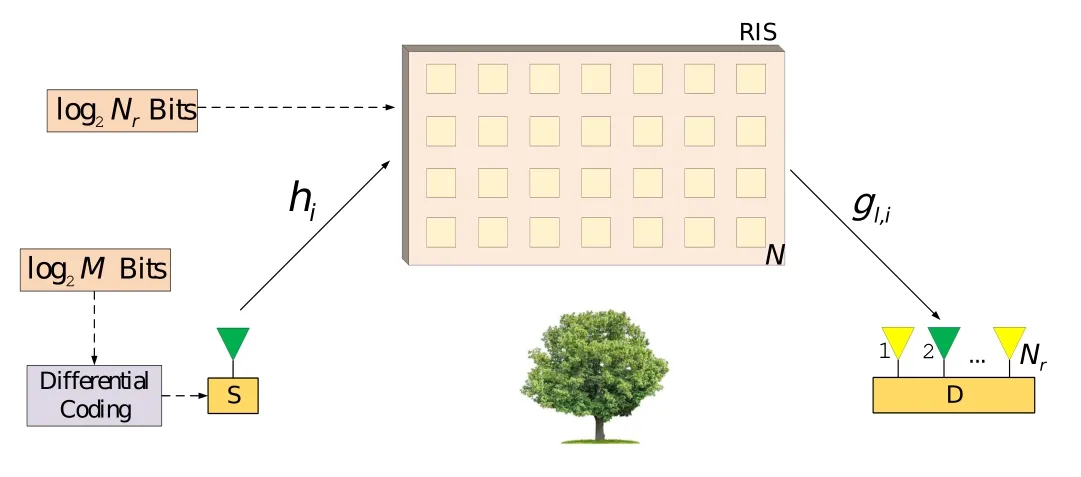
Figure 1.System model of the proposed RIS-DSM scheme.

2.1 Differential Transmission Process

As illustrated in Figure 1,the data bits are separated into two distinct segments.In this scenario,both S and RIS do not share the data bits and they must transmit their respective data independently.While the first part of log2Mbits will be used to select the modulated symbol fromM-PSK constellation,the second part of log2Nrbits will be used to select a specific receive antenna by adjusting the RIS phases,which will maximize the instantaneous received SNR.We assume thatxtis the selected modulated symbol int-th time slot andstrepresents the actually transmitted modulated symbol int-th time slot.At the beginning,S transmits an arbitrary initial modulated symbols0and the RIS selects an arbitrary initial receive antennal0,which may be unknown to D.Since symbol 1 is always included in theM-PSK constellation,we chooses0=1 without loss of generality.Note thats0andl0do not convey any data.Thereafter,the transmitted modulated symbolstint-th time slot is generated in a recursive differential coding manner.As a result,the method of transmitting with the RIS-DSM scheme consists of the following steps:

Step 1:Map the first log2Mbits onto theM-PSK constellation to getxt.

Step 2:Compute the transmitted modulated symbolstby

and then transmit it to RIS.

Step 3:RIS reflectsstto the receive antenna selected by log2Nrbits.

The aforementioned three steps are repeated till the transmission is finished.

2.2 Detection Method

Letylbe the received signal at thel-th receive antenna of the D,the received signalylin thet-th time slot can be represented as

where E[|st|2]=Es,and the average energy per modulated symbol transmitted is denoted byEs.nt∼CN(0,N0) representst-th time slot’s additive white Gaussian noise (AWGN).Thel-th receive antenna’s instantaneous SNR is calculated as

In order to maximize the instantaneous SNR at the specified receive antenna,the log2Nrincoming bits are used to identify the indexmof the receive antenna and the RIS adjusts its phases accordingly for alli,asϕi=ψl,i+θifor that particular receive antenna.Accordingly,the maximum instantaneous SNR at the specific receive antenna can be calculated as

Therefore,the signal received at them-th selected receive antenna can be denoted asym.In this way,ym,t-1andym,trepresent the received signalsymat the(t-1)-th andt-th time slots,respectively.As indicated by(4),we possess

Assume that the fading coefficients are constant throughout two adjacent transmitted symbols in a quasi-static channel.By substituting (1) and (5) into(6),ym,tcan be expressed as

To detect the modulated symbolxt,the receive antenna indexmwhich provides the highest instantaneous SNR is first determined.Thus,using the greedy detector,we can get the receive antenna indexm,which is denoted by

Based on the correct index of receive antenna detection,through non-coherent detection the modulated symbolxtat them-th receive antenna can be obtained

as

III.PERFORMANCE ANALYSIS

In this section,we derive the theoretical ABEP of the proposed RIS-DSM scheme.Since the receive antenna indexmand modulated symbolxtare detected separately,we use the following approximation[12]

where the average correct detection probability of receive antenna indexmis denoted byPc(m),Pe(m)denotes the average erroneous detection probability of the indexmwherePe(m)=1-Pc(m),andPb(xt)denotes the average bit erroneous detection probability of modulated symbolxtconditioned on correct index of receive antenna detection.Here,we follow a conservative approach: since the receiver does not make a correct decision on receive antenna index,the correct probability of modulated symbol index is simply equal to 0.5[23,24].

3.1 Analysis of Pe(m)

To clarify the derivation of the optimal RIS phase,we take into account the case when the receive antenna indexmis incorrectly detected as ˆm.Based on the detection rule given in(8),we can calculate the corresponding pairwise error probability(PEP)as

σ1,2is the covariance ofC1andC2,which can be given as

Then the moment generation function(MGF)ofCcan be calculated from[25]as

The complexity of the distribution ofCmakes it necessary to use the Gil-Pelaez’s inversion formula [25]in order to calculate the PEP ofmas

P(m→|st)is dependent onstforM>4,and the average PEP for index detection can be calculated as

Thus,Pe(m)can be upper bounded as

3.2 Analysis of Pb(xt)

In this section,we assume that the receive antenna indexmis accurately estimated.Thus,conditioned on received signal,the PEP of modulated symbolxtcan be expressed as

Similar to previous relevant calculations,htfollows Gaussian distribution.According to the CLT,we have E[ht]=Nπ/4,Var[ht]=N(1 -π2/16) when the number of reflecting elements becomes very large,namelyN≫1.Then,the MGF of Γ,a non-central chi-square RV with one degree of freedom,is given as follows

wheres=-1/4 sin2ηN0.Then,we can substitute(25)in(24)and calculate the numerical integration to get the averaged PEP ofxt.The averaged PEP values derived from (24) can be used to calculate the union bound on the ABEP

wheree(xt→)represents the number of incorrect bits in a given pairwise error event.Finally,substituting(19)and(26)into(10)yields the theoretical value ofPb.

IV.DETECTION COMPLEXITY ANALYSIS

In this section,we evaluate the RIS-DSM scheme’s detection complexity and compare it with RIS-SM,RIS-SSK,DRM,single-input multiple-output(SIMO)schemes.The greedy detector needsNrreal multiplications to identify the chosen receive antenna index,as indicated by (9).And for (10),the computation ofneeds to considerMpossibilities ofxt,Msquared complex modulus operations andMreal summations(RSs).Consequently,the detection complexity of RIS-DSM scheme is obtained as 2M+NrRMs andMRSs.Next,we simplify the detection complexity to improve the efficiency of detection.Sinceis a real variable,the received signalymcan be regarded as a PSK constellation amplified byβm,itimes under the AWGN.Thus,we can makeandbe in the same quadrant to find the minimum value of,in whichxtcan be selected fromM/4 PSK constellation whenM≥4.Finally,the detection complexity of RISDSM scheme is simplified asM/2+Nr(M≥4)or 2+Nr(M=2) RMs as well as 2(M=2) orM/4(M≥4)RSs.

The results of the complexity analysis findings in terms of the number of RMs and RSs,are summarized in Table 1.For comparison,the complexity of RIS-SM and RIS-SSK with both ML detection(MLD)and greedy detection(GD)are included in Table 1,respectively.On the other hand,we also investigated the complexity of SIMO with PSK signaling (SIMOPSK) and differential PSK signaling (SIMO-DPSK)schemes.It is shown from Table 1,besides modulation ordersMand the number of receive antennasNr,the detection complexity of DRM is also determined by reflecting pattern candidatesK.Moreover,one can see that the RIS-DSM scheme has the lowest detection complexity by excluding the RIS-SSK(with GD)scheme.

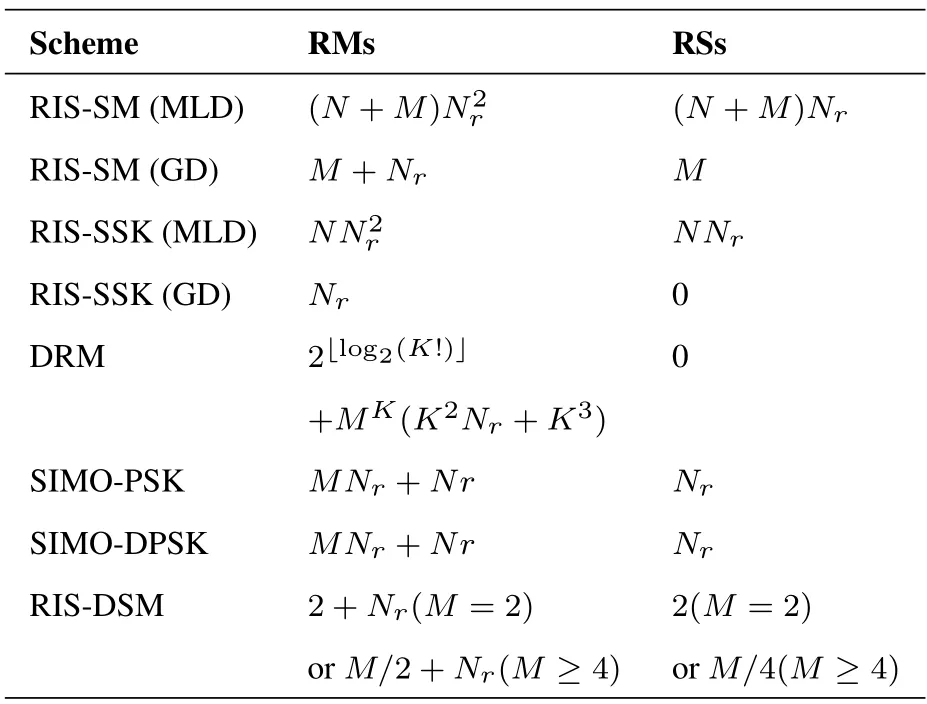
Table 1.Complexity analysis summery.

V.SIMULATION RESULTS

In this section,the proposed RIS-DSM scheme’s BER performance is evaluated through simulations.Additionally,the performance of reference systems in terms of BER is also evaluated for comparison.The SNR is defined asEs/N0and the path-loss at large scale is not taken into account here.In Figures 2-5,the BER is depicted on they-axis,while the SNR is presented on thex-axis.

In Figure 2,we compare the theoretical BER and simulated BER values of RIS-DSM for different numbers of reflecting elementsN,modulation ordersMand receive antennasNr.The theoretical values of BER and the simulation results gradually match asNincreases.Furthermore,we observe that the effect of increasingNrwill not cause the BER of RIS-DSM scheme to drop significantly.While increasingM,the BER degradation is more evident.

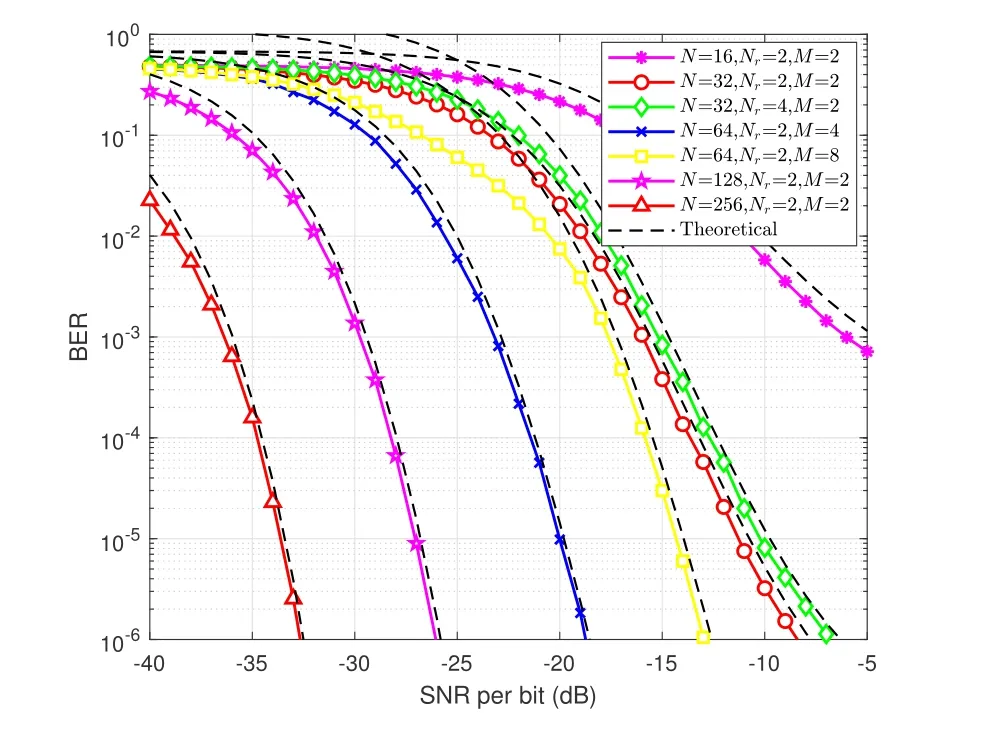
Figure 2.Theoretical and simulation results for RIS-DSM.

Figure 3 compares the BER performance of the RISDSM and RIS-SM schemes at different bits per channel usage(bpcu).As observed from the left subfigure,the BER performance of RIS-DSM is very close to that of RIS-DSM with GD.The BER performance of RISDSM is slightly worse than that of the RIS-SM scheme when MLD is used.However,when the number of elementsNis increased from 64 to 128,the BER performance gap between RIS-DSM and RIS-SM with MLD can be reduced from around 2 dB to 1 dB.Figure 3 also compares the BER performance of RIS-DSM and RIS-SSK schemes for various bpcu values.The right subfigure shows that the RIS-DSM scheme performs about 1 dB better than the RIS-SSK scheme with GD.In contrast,when the ML detector is employed for the RIS-SSK scheme with complete CSI,its BER performance is superior to that of the RIS-DSM scheme.The BER performance of the RIS-DSM scheme is acceptable given the low detection complexity,especially for high SE values,using the same hardware facilities.

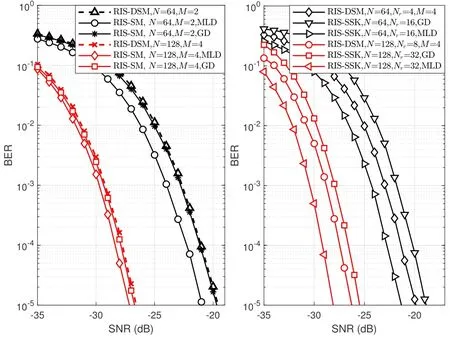
Figure 3.Comparison of the BER performance of the RIS-DSM scheme with RIS-SM scheme(left),and RIS-SSK scheme(right).

Figure 4 compares the BER performance of the RISDSM scheme to the performance of both the PRM and the DRM schemes.It is important to note thatis the number of ON-state elements in PRM scheme.Thus,totally log2M+data bits can be conveyed in PRM scheme.Figure 4 presents several important observations.First,it is obvious that BER curves of the RIS-DSM scheme demonstrate both a waterfall region and a saturation region.Second,the PRM scheme does achieve a high beamforming gain with part-ON RIS reflection,but will lose part of the received power.The RIS-DSM scheme can achieve high data-rate transmission in a simple and effective way,but it needs to activate more reflector elements for better performance.Third,the benefits of the RIS-DSM scheme are primarily reflected in the waterfall region,when compared to the DRM scheme.

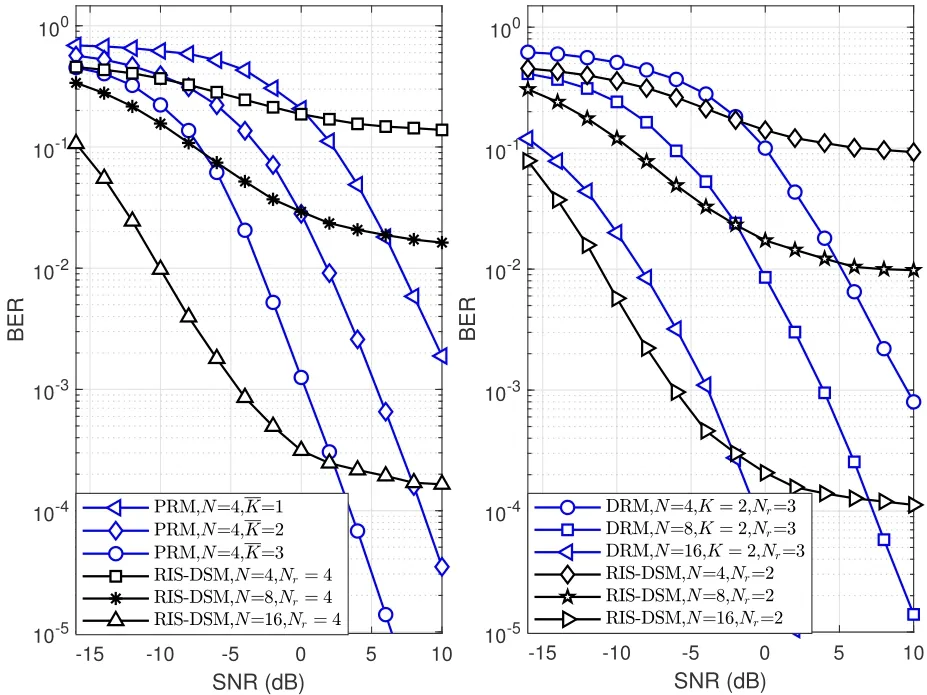
Figure 4.Comparison of the BER performance of the RISDSM scheme with PRM scheme for BPSK signaling (left),and DRM scheme for QPSK signaling(right).

Lastly,the BER performance of the RIS-DSM is compared to that of the SIMO-PSK and SIMO-DPSK schemes in Figure 5.Q-PSK modulation is utilized for SIMO-PSK and SIMO-DPSK schemes during the performance comparison,and the values ofNrandMin RIS-DSM scheme are both 2.It can be seen that the BER performance of the RIS-DSM scheme is superior in the waterfall region but inferior in the saturation region compared to the SIMO-PSK and SIMODPSK schemes.For instance,the proposed scheme has approximately 7 dB improvement with respect to SIMO-PSK and 12 dB improvement with respect to SIMO-DPSK whenN=16,BER=10-2.Furthermore,the performance advantage of waterfall region becomes more obvious with increasingN.

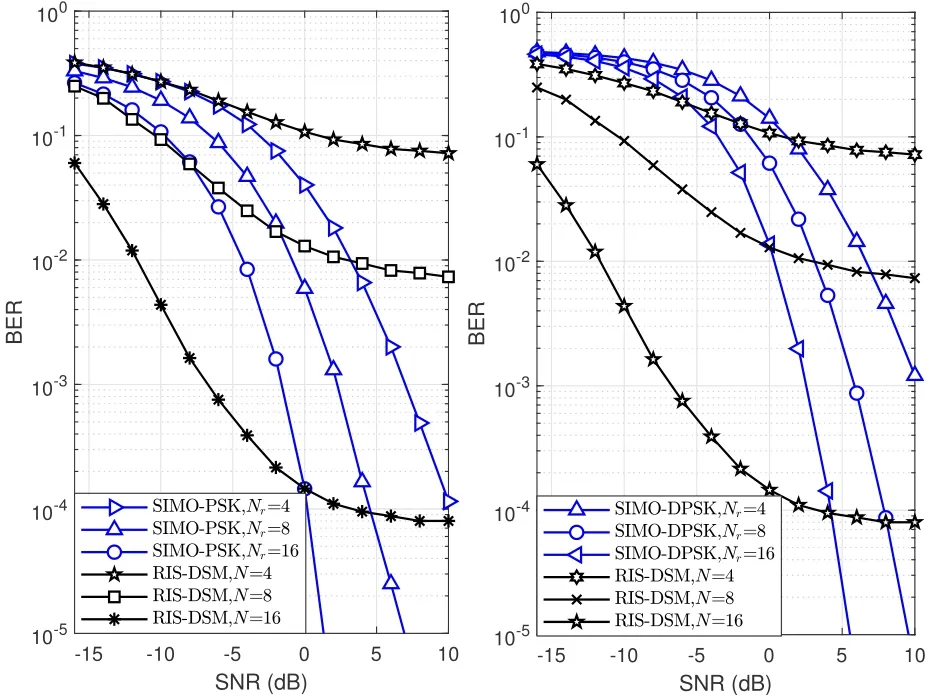
Figure 5.Comparison of the BER performance of the RISDSM scheme with SIMO scheme (left),and DPSK scheme(right).

VI.CONCLUSION

In this paper,a new differential technique was suggested for the RIS-SM to eliminate the requirement of receiver-side CSI.In our proposed RIS-DSM scheme,the incoming data bits were respectively mapped into receive antenna index and modulated symbol instead of conventional information matrices,which improved the SE.Moreover,the performance of the proposed scheme was evaluated using the derived ABEP.The results of the proposed RIS-DSM scheme were validated through simulations that demonstrated its advantages in terms of BER performance and detection complexity compared to the theoretical results.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China(No.61801106).