血管中血液的粘弹性流动分析

田长留,花少震

(河南工学院 机械工程学院,河南 新乡 453003)

0 引言

血液是一种复杂的悬浮液体,主要由红细胞、白细胞、血小板、电解质、水等组成[1]。人体中的血液在营养输送、维持体内环境平衡和防御功能等方面起着重要作用对血液的研究已经成为医学科学的一个重要组成部分,其中血液在心血管中的流动问题是当前生物力学研究中较为活跃的分支之一。随着计算机技术的不断提高,越来越多的科研工作者采用数值手段模拟血管中血液的流动[2-4],目的是根据血液动力学因素(压力、剪切速率等)和血液流变学性质(粘度、粘弹性)为一些现象(触变性、血小板激活、凝血块)以及血管类疾病(动脉硬化、动脉瘤等)的研究提供参考和借鉴。现有的血液数值计算中常将血液视做理想流体或者仅考虑粘性的非牛顿流体[5],然而血浆中含有7%—10%的大分子蛋白质,具有明显的粘弹性(viscoelastic)特征。粘弹性流体同时表现出粘性和弹性,其流变特征在很多方面都表现出和粘性流体很不同的规律,有时候甚至出现截然相反的流动现象[6]。虽然血液具有粘弹性性质,但是由于粘弹性数值求解的限制,目前对血液流动的数值模仿真中一般忽略血液的弹性,仅将血液视作理想流体或粘性流体。当血液在一个直径比较大的血管(如主动脉等)中流动时,此时血液流动的雷诺数Re比较大,可将血液视作理想流体[7];研究血液和血管流固耦合仿真时也将血液视作理想流体[8];当血液在直径较小的血管(如毛细血管、小动脉、小静脉等)中流动时,此时剪切速率较小,剪切变稀效应明显,可将血液视作非牛顿流体[9]。另一种理论认为,当血液流动产生的剪切速率小于100s-1时,血液的非牛顿流体性质明显;当剪切速率大于100s-1时,可将血液视作牛顿流体。但是,相同位置处的血液在一个循环周期内产生的剪切速率始终是变化的。以大动脉为例,在一个循环周期内,血液流动的剪切速率可从0增长到1000s-1,因此究竟将血液视作牛顿流体还是非牛顿流体,要视情况而定[10]。

尽管对血液在血管中流动仿真的关注日益增强,但是仍然缺少关于血液粘弹性流动的数值模拟研究。本文拟在考虑血液流动过程中的粘弹性流变行为基础上,构建粘弹性算法,模拟血液在血管中的粘弹性流动,探寻血液在血管中流动的粘弹性质。

1 血液在血管中流动粘弹性数学模型

假设血液在血管中流动时为不可压缩流体,忽略其温度的变化,根据血液在血管中流动的质量守恒和动量守恒,则可得到控制方程:

·u=0

(1)

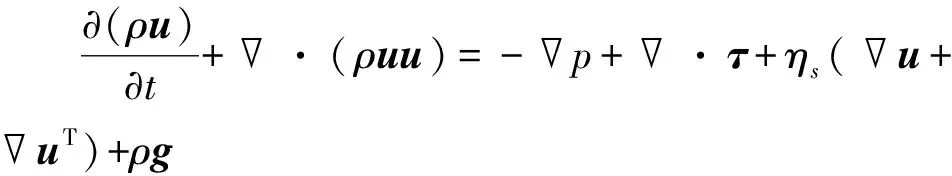
(2)

式中,ρ为血液密度,u、p分别为速度和压力,ηs(u+uT)代表粘性所贡献偏应力,τ通过求解粘弹本构方程获得。采用Giesekus本构模型表征血液的粘弹流变性质,则有:

(3)

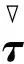
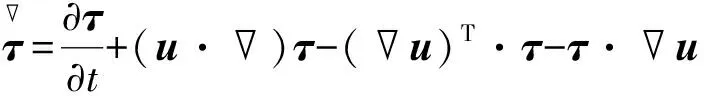
(4)

2 数值算法

采用有限体积法离散控制方程(1)、(2)和粘弹性本构方程(3)、(4)。对于任一时间步长Δt,由于速度、压力及速度、应力之间的高耦合性,采用PISO(Pressure-Implicit with Splitting of Operators)算求解法速度-压力,然后将t+Δt时刻的速度作为已知量,进而求解应力。首先,可将式(3)、(4)整理为含瞬态项、对流项和源项的偏微分方程:

(5)

(6)

式中,下标f为对应控制体的f面上的物理量,Vp为控制体体积。求解式(6)即可得到t+Δt时刻的偏应力张量τ。黏弹性流动求解的难点在于算法的不稳定性,为了得到高稳定性算法,本文借鉴DEVSS(Discrete Elastic Viscous Split-Stress)算法,将该算法从有限元算法扩展到有限体积法,则(2)式调整为:

(7)

式中,等号右边为源项,φ(ut)=-p+·τ+ρg-·(ηsut)。将(7)式采用有限体积法离散,则有:

(8)

式中,n代表单位外法向量,A为控制体的面的面积大小。联立(1)式和(8)式,即可用PISO算法求得t+Δt时刻血液在血管中流动过程中速度u和压力p的大小。

3 血液在血管中流动数值模拟

建立人体血管的三维简化模型,如图1所示,其中血管的直径为2mm,入口到A截面、C截面到出口为直管,ABC为等曲率弯管,其曲率半径为2mm。血液所对应的粘弹性参数为:η=0.0025Pa·s,ηs=0.0025Pa·s,λ=0.015s,α=0.3。血液的流动速度为0.13m/s。采用上文所发展粘弹性算法模拟血液在图1所示血管中的粘弹性流动,并取A、B两个截面为研究对象,分析其粘弹性流动。由于C截面为弯管的末端,直管的始端,其流动特征和A截面差别较小,在此不单独分析C截面的粘弹性流动。

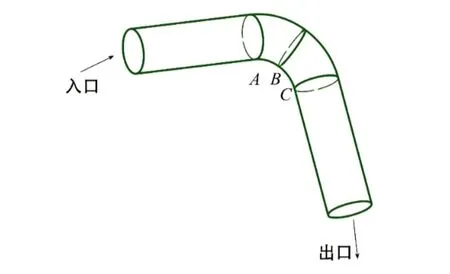
图1 血管三维简化模型

图2(a)和图2(b)分别为A、B截面上的二次流,图中圆截面上部和下部分别代表A、B截面在弯管的内侧和外侧。A截面为弯管始端,速度矢量为绕截面流动的环流,速度大小由截面外层到圆心逐渐减小。数值结果表明,A截面上环流强度约为主流的百万分之一。B截面位于ABC弯管的中部,如图2(a)所示,其截面上速度矢量表现出两个关于垂直于弯曲方向且两边对称的涡,涡的强度约为主流的千分之一。涡的方向总是由内侧中心点沿圆心附近区域向外侧中心点流动。随着流动距离的增加,由于内摩擦等因素,剪切速率不断降低,惯性力减少而粘性力逐渐增大,在驱动力不变情况下,速度先增大后减小,且离圆心越近速度越大。然后,涡流沿血管外侧中心点沿截面外层回流至内侧中心点。由于靠近血管壁处的剪切速率比较大,粘弹性流体的第二法向应力差占主导作用,速度不断增大。

(a)B截面上的涡流

图2(a)显示涡由内侧中心点沿圆心附近区域向外侧中心点流动,由于流体总是从压力高的区域流向压力低的区域,所以弯曲血管内侧的血液流动压力高于血管外侧的血液流动压力。图3为B截面上压力的分布云图,其单位为kPa。由于A截面为等直血管的末端,其受直管中流动科式力的影响较大,内外侧压力、速度分布差别较小,本文不作展示和分析。考虑血液的粘弹性质后,从B截面压力分布可以发现,由于涡关于内外侧直径对称,所以对于压力的分布也关于内外侧直径对称。弯曲血管内侧到外侧的压力逐渐减小,这和传统黏性流体在弯管中流动时内外侧压力分布规律相反。黏性流体在弯管中的流动时外管侧的压力大于内管侧的压力[11]。本文中,考虑血液的弹性后,由于第二法向应力差作用,使得弯曲血管内侧压力大,弯管内侧最大压力为15.25kPa,外侧最小压力为14.25kPa,内外侧最大压力差达到0.8kPa。对于直线型血管A截面,考虑血液流动后,横截面上压力差别较小。

图3 B截面上压力分布(圆截面上部为弯管内侧,单位kPa)

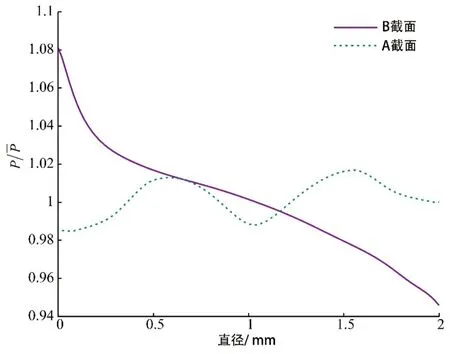
图4 A、B截面上由内侧到外侧直径上的压力P同平均压力的比值分布

上文分析了血液在弯曲血管和等截面直管中的粘弹性流动,数值结果研究表明血液的弹性对血液在等截面直血管中的流动影响较小,但是血液的弹性对于血液在弯曲血管中的流动非常重要。可以发现由于血液的粘弹性,弯曲血管内侧的血压要大于外侧的血压,即血液在流动过程中对弯曲血管内侧的冲击更强,也即血管内侧的血管壁所需要承受的压力更大。而且由于内侧血液流速缓慢,当血液流动的惯性作用小于黏滞力时,弯曲血液内侧中的蛋白质、脂肪等大分子即有可能停止流动,附于血管内壁,导致一些疾病。

图5 B截面上由内侧到外侧直径上的速度大小

4 结语

本文基于Giesekus本构关系建立了血液的等温不可压缩的粘弹性流动模型,采用有限体积法离散控制方程,发展了血液的粘弹性流动算法。在对等直血管和弯曲血管的血液流动仿真中发现血液的粘弹性对弯曲血管的作用更为明显。和粘性流体在弯管中流动时内侧压力低、外侧压力高的特点相反,血液的粘弹性使其在流动过程中对弯曲血管内侧的冲击要强于外侧。本文算法能有效模拟血液在血管内的粘弹性流动,可以为一些血液类疾病的病因分析与治疗以及相关的生物医学工程提供借鉴。