基于Spark大数据计算模型的遗传算法深度前馈神经网络训练算法
任 刚,李 鑫,刘小杰,张 阳,郜广兰,4,肖东栩
(1.河南工学院 计算机科学与技术学院,河南 新乡 453003;2.中国矿业大学 计算机科学与技术学院,江苏 徐州 221116;3. 河南省生产制造物联大数据工程技术研究中心,河南 新乡 453003;4.新乡市虚拟现实与系统重点实验室,河南 新乡 453003;5.河南大学 欧亚国际学院,河南 开封 475000)
0 引言
人工神经网络(Artificial Neural Network, ANN)是一种模拟人脑神经节点信号传递的计算模型,该模型可通过大量数据学习找出潜在规律,在很多领域得到了广泛应用。深度前馈神经神经网络(Deep Feedforward Neural Network, DFNN)是一种应用较为广泛的人工神经网络[1],该模型采用信号向前传递的多层网络结构,可通过训练方式优化神经网络节点间权值和阀值,并利用训练过的模型进行预测,其模型训练算法是重点研究内容之一[2]。
遗传算法(Genetic Algorithm, GA)是一种借鉴生物界自然选择和遗传机制的全局随机搜索算法,该算法把问题可能解看作种群个体, 多个个体组成1个种群,通过对种群个体使用选择、交叉和变异3个遗传算子,使种群不断进化,直至产生近似最优解。该算法在全局寻优上表现出鲁棒性和高效性,被广泛应用于各类组合优化问题求解[3]。
遗传算法深度前馈神经网络(Genetic Algorithm Deep Feedforward Neural Network, GADFNN)是一种利用遗传算法对深度前馈神经网络模型进行训练的算法。由于综合了遗传算法在全局寻优的优势和深度前馈神经网络在非线性逼近问题上的优势,因此,该算法具有较好的计算效率和预测精度,在分类和回归问题上应用广泛[4-6]。但是,该类模型传统训练算法属于单机版串行算法,在样本规模较大时,训练时间往往较长,难以满足实际应用对计算时间的要求。
近年来,随着数据采集技术的不断提高,遗传算法深度前馈神经网络模型训练样本呈现出明显的大数据特点[7],传统的单机版训练算法受到很大挑战,迫切需要一个支持数据并行的训练算法来满足大数据样本训练的需要[8]。
Spark[9]是一种基于内存的大数据并行计算开源模型,该模型将大数据集分割成多个小数据块,分配到多个计算节点,各计算节点通过并行计算提高计算效率。该模型通过数据转换完成业务逻辑计算,具有编程模型简单、计算高效的特点,被广泛应用于大数据分析。Spark的高效性为实现数据并行训练算法提供了一个可能的选择。但是,由于该模型具有其特有数据编码和转换规则,据了解,目前尚无较成熟方法在Spark模型上实现遗传算法深度前馈神经网络训练。
为此,本文将首先研究Spark模型数据编码和转换规则与遗传算法深度前馈神经网络模型训练计算过程的内在对应关系,提出一个基于Spark模型的遗传算法深度前馈神经网络训练算法——Spark-GADFNN。
1 遗传算法深度前馈神经网络模型
1.1 深度前馈神经网络模型
深度前馈神经网络[10]是一种单向多层网络模型,每层包含多个神经元节点,各层神经元接前一层神经网元信号,并将结果输送到下一层节点。图1是一个具有L层的网络模型,0层是输入层(Input Layer),L层是输出层(Output Layer),其余层是隐含层(Hidden Layers)。
l层神经节点j的输出分两步计算,首先使用公式(1)计算l-1层输入集:
(1)
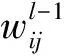
深度前馈神经网络需要一个激活函数来触发神经元输出,本文使用在实际中应用较为广泛的S型函数,如式(2)所示:
(2)
这样,第l层节点j输出为:
(3)

1.2 遗传算法深度前馈神经网络训练算法
经典深度前馈神经网络训练算法包括输入样本数据(Input sample data)、确定神经网络结构(Determination of NN structure)、初始化权值和阀值(Initialization of weight and threshold)、权值和阀值训练((Training of weight and threshold)和收敛判断(Determination convergence)等5个基本计算过程,该模型通过收敛判断控制训练迭代过程,一次训练过程往往需要多次迭代来完成,整个训练过程如图2左侧子图所示。
遗传算法包括种群初始化(Initialization of population)、评估(Evaluation)、选择(Selection)、交叉(Crossover)、变异(Mutation)和收敛判断(Determination of convergence)等6个基本计算过程,其中,收敛判断通过设定条件负责决定迭代终止,整个过程如图2中间子图所示。
遗传算法深度前馈神经网络模型训练算法基本实现方法是将神经网络训练过程映射到遗传算法计算过程中,通过遗传算法迭代来实现深度前馈神经网络模型训练过程。具体来说,输入样本数据、确定神经网络结构、初始化权重和阀值在种群初始化过程中实现,权值和阀值训练由遗传算法评估、选择、交叉和变异过程完成,神经网络收敛判断直接映射为遗传算法收敛判断等,通过收敛判断决定是否迭代。具体映射关系如图2左侧映射关系所示。
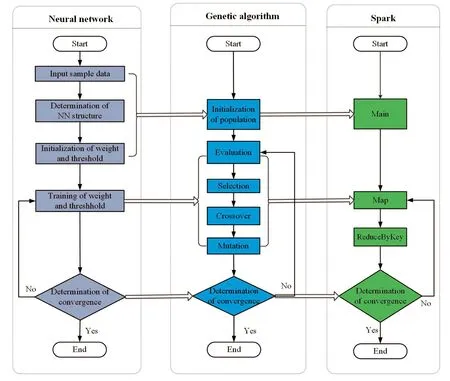
图2 Spark-GADFNN训练算法映射关系
1.3 基于Spark模型的遗传算法深度前馈神经网络训练算法
Spark是一种基于Hadoop分布式文件系统(Hadoop Distributed File System, HDFS)的大数据并行计算模型,以弹性分布式数据集(Resilient Distributed Dataset, RDD)为核心的并行计算模型,RDD是基于内存的只读数据集合,通过转换(Transformation)操作完成RDD的处理,转换操作主要包括map和reduceByKey等操作,map转换属于窄依赖转换,reduceByKey属于宽依赖转换,会触发shuffle过程。
Spark模型采用分布式并行计算架构,首先从HDFS中读取数据,形成RDD,此RDD一般分布存储在各集群计算节点内存中。然后,针对RDD,通过一系列转换操作,形成新的RDD,最终结果重新写回HDFS,各RDD数据转换操作采用并行计算模型,以此提高数据处理效率,Spark并行架构如图3所示。
在利用RDD进行遗传算法迭代操作时,通常采用键值对RDD这种数据集合形式,该数据集合每个元素都是(key,value)键值对类型,主要通过map和reduceByKey操作完成业务逻辑。
map输入为(key1,value1),通过map操作根据具体业务逻辑输出新的键值对(key2,value2),map操作键值对转换形式定义如下:
map:: (key1,value1)→(key2,value2)
(4)
reduceByKey会接收来自map的输出(key2,value2),此时,Spark模型会启动shuffle操作,该操作通过全局通信,将分布于不同RDD的键值对,按照key2值进行连接,发送给reduceByKey操作,shuffle操作键值对转换形式定义如下:
shuffle:: (key2,value2)→(key2, list(value2))
(5)
reduceByKey操作收到(key2, list(value2))后,根据业务规则聚合成value3,并形成新键值(key3,value3),reduceByKey键值对转换形式定义如下:
reduceByKey:: (key2, list(value2))→(key3,value3)
(6)

图3 Spark分布式并行计算架构
1.4 Spark-GADFNN算法实现
提出的Spark-GADFNN算法实现的关键,首先在于确定遗传算法计算过程到Spark计算过程的映射关系。如图2右侧映射关系所示,提出的Spark-GADFNN算法在Main函数中实现种群初始化,遗传算法迭代过程由map、reduceByKey和收敛判定(Determination of convergence)操作完成,map负责遗传算法的评估、选择、交叉和变异过程,以完成种群进化。
reduceByKey操作负责收集来自map输出的种群信息,搜索全局最优解,并产生下一代种群。遗传算法收敛判断直接映射为Spark-GADFNN的收敛判断过程。在具体实现上,为了进一步提高效率,该过程与reduceByKey过程合并为一个计算过程。
提出的Spark-GADFNN算法中,遗传个体编码形式化定义为:
ind=
(7)
式中,code为个体编码,fitness为个体适应度。这样,具有n个个体种群可形式化表示为:
(8)
popValueij=
(9)
populationij表示第j代种群i,popKeyi表示种群i关键字,迭代过程中该值保持恒定。Pcij和Pmij分别表示该子种群的交叉和变异概率,bestInd记录该种群局部最优解,indkij表示该种群第k个体。
提出的Spark-GADFNN实现的另一个关键问题是确定map和reduceByKey的键值对转化过程,转化过程如图4所示。种群以文件形式在HDFS,map每次读取1个种群信息,形成键值对(key1,value1),如下所示:
key1=popKeyi
(10)
value1=popValueij
(11)

图4 Spark-GADFNN训练算法数据转换过程
为了后继shuffle过程中不同种群个体都能被送到同一个reducebyKey过程,以便找出全局最优解,并共享该值,将key2设置为0。同时,为了在下1次迭代中,保持种群稳定性,popKeyi作为普通数据元素,暂存在value2中,(key2,value2)形式定义如下所示:
key2=0
(12)
value2=popKeyi∪popValuei(j+1)
(13)
map实现主要代码如下:map首先使用Evaluation函数计算value1中每个个体ind个体适应度,并更新当前种群最优解。然后,从value1中取出交叉概率和变异概率,并依次进行选择、交叉和变异操作,并更新种群,此时,产生新一代种群值popValuei(j+1)。最后,输出(key2,value2)键值对。

Algorithm 1: mapInput: (key1,value1);Output: (key2, value2)01for each ind in value1 do02 if ind.fitness==Null do03 Evaluation(ind);04 end if05 if ind.fitness> bestInd.fitness do06 value1.bestInd=ind;07 end if08end for09Pm=value1.getPm();10Pc=value1.getPc();11for (i=0; i++; i Algorithm 1: map 14 {I″1, I″2}=Mutation({I'1, I'2}, Pm);15 value1=value1-{I1, I2}+{I″1, I″2};16end for17key2=0;18value2={key1}+value1;19EMIT(key2, value2); 生成(key2,value2)后,Spark模型启动shuffle过程,具有相同key2的value2被连接为新的键值对(key2,list(value2))。由于算法1将key2设置为0,所以,所有value2被链接在一起,形成list(value2)。这意味着,所有种群被聚合在一起,以便寻找全局最优解。这一步是算法实现的关键步骤,即利用Spark系统提供shuffle机制完成种群聚合。 reduceByKey接收到来自Spark系统传来的(key2,list(value2)),负责将其转换为(key3,value3),作为下次的迭代输入。为了保持种群稳定性,将暂存在list(value2)中的popKeyi取出,赋于key3。同时,用全局最优解替换value2中的局部最优解,输出键值对(key3,value3)如下所示: key3=popKeyi (14) value3=value2+{globalInd}-{bestInd} (15) reduceByKey操作首先查找全局最优解globalInd,然后通过Convergence函数判断收敛条件。收敛有两个条件,一个是现有全局最优解满足预定条件,一个是达到最大迭代次。若满足收敛,则直接结束;否则,用当前全局最优解替换各种群,最后生成键值对(key3,value3)。具体实现如算法2所示。 Algorithm 2: reduceByKey Input: (key2, list(value2))Output: (key3,value3)01for each value2 in list(value2) do02 if bestInd.fitness> globalInd.fitness do03 globalInd=bestInd;04 end if05end for06if convergence(key2, value2)==TRUE do07 return globalInd;08end if09for each value2 in list(value2)do10 value3=value2+{globalInd}-{bestInd};11 key3=value2.getPopKey();12 value3=value2-{key3};13 EMIT(key3, value3);14end for 通过三组实验比较传统GADFNN训练算法[5]与提出的Spark-GADFNN训练算法在预测精度和训练效率上的表现。采用UCI实验室提供的Lung Cancer (LC)[11]、Beijing PM2.5 Data (BPM2.5D)[12]和Heterogeneity Activity Recognition (HAR)[13]三个数据集,其基本信息如表1所示,取样本数90%作为测试数据集,10%作为验证数据集。 表1 实验数据集 计算节点从1递增至8,算法迭代80次自动结束,记录运行时间,单位为秒,实验主要参数设置如表2所示,计算结果如表3所示。由表3可以看出,在小规模数据集LC上,随着计算节点个数增加,计算时间没有减少,反而增加,计算节点扩展性不佳,其原因在于该数据集规模过小,系统通信成本和数据存储时间在整个计算时间上占了大部分。对于中等规模数据集和大规模数据集算法,随着计算节点的增加,训练时间逐步减少,表现出良好的扩展性。同时确定,在小规模数据集LC上,算法最佳计算节点为1,在中等规模数据集BPM2.5D和大规模数据集HAR上,最佳计算节点数都为8。 表2 实验参数 表3 计算节点扩展性分析 迭代次数从10逐步扩展到80,记录不同迭代次数下模型预测精度,GADFNN采用单机版算法,Spark-GADFNN计算节点数在小规模数据集LC上设置为1,在中规模和小规模数据集上皆设置为8,该数据是实验1给出的最佳并行计算节点数,实验结果展示在表4,由表4可以看出,对于三种规模数据集,两算法在迭代过程中,误差率始终不大;还可以看出,两算法的计算误差都在40次迭代后达到稳定,误差均相同。这说明数据集规模对于算法收敛速度和预测精度无显著影响,其原因在于提出的算法和原算法仅在计算方式上有区别,并没有改变原算法的计算原理。该实验表明本文提出的算法保留了原算法在收敛速度和预测精度误差上的优势。 两算法迭代次数都取40,实验2证明该数值下两算法均收敛。Spark-GADFNN算法在LC、BPM2.5D和HAR数据集上,计算节点数分别设置为1、8、8,这是实验1给出最佳计算节点数,时间单位为秒,计算结果如表5所示。由表5可以看出,在小规模数据集LC上,本文算法耗时较多,在时间上无优势,其原因在于Spark计算模型在单节点计算模式下,数据存储和模块通信都消耗一部分时间,其性能不如普通单机版串行算法。 在中等规模数据集BPM2.5D和大规模数据集HAR上,本文算法训练时间分别缩短为原算法的18.18%和16.67%,计算时间明显缩短,其原因在于数据集被平均分配到8个计算节点上,Spark计算模型的优势得以发挥。实验表明,本文算法在中、大规模数据集上训练时间具有明显优势。 表4 预测精度分析 表5 训练时间分析 提出了一个基于Spark大数据计算模型的遗传算法深度前馈神经网络模型训练算法Spark-GADFNN,该算法实现了经典遗传算法深度前馈神经网络模型训练算法数据并行。实验表明,在中、大规模数据集上,该算法训练时间分别缩短到原算法18.18%和16.67%。下一步可研究利用Spark模型实现其他网络模型训练算法的并行化。

2 性能验证

2.1 实验1:计算节点扩展性


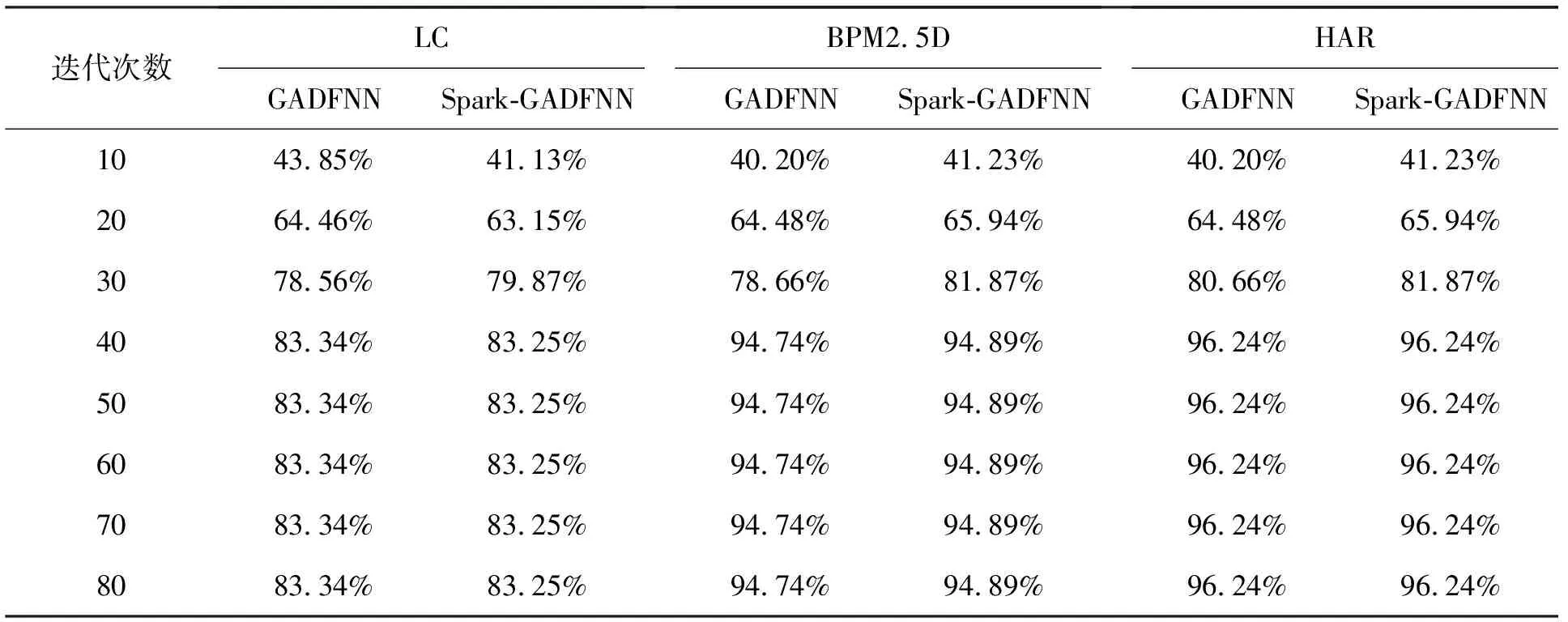
2.2 实验2:预测精度分析
2.3 实验3:训练时间分析

3 总结

