用活一边一角，探究几何全等构造

夏明

大连市金州区南金实验学校张磊老师的直播课“基于一边一角构造全等三角形的策略”选自辽宁教育学院“学到汇”公众服务平台“辽宁省初中数学学科周末名师公益课堂”，旨在贯彻落实国家“双减”政策，帮助广大师生自主学习和个性化提升。

观看了张磊老师的这节直播课，同学们就会发现：如果能找到一边一角相等，就可以轻松构造一个新的三角形与原三角形全等.

模型解读

模型1：一边一等角

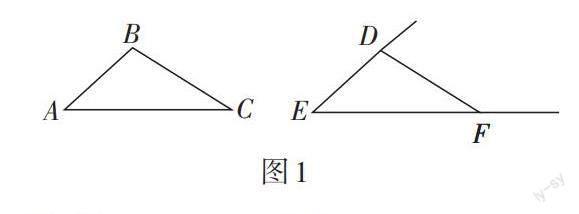
1.相等边是已知条件.如图1，AB = DE，∠A = ∠E，可把△ABC作为目标三角形，以DE为边作与之全等的三角形.方法1：DE在∠E的一边上，在∠E的另一边上截取EF = AC，可得△DEF≌△BAC（SAS）. 方法2：以点D为顶点，作∠EDF = ∠B，可得△DEF≌△BAC（ASA）.

2.相等边是所求结论.可用上述方法2：在边的另一端作相等的角.作图后可得两个结论：已知一组角相等（∠A = ∠E），如图1；作一组角相等（∠EDF = ∠B）.往往是要通过第三组角相等（∠ACB = ∠EFD），推导出一条边相等，从而得到一组三角形全等 （△ABC ≌△EDF）.

模型2：一边一互补角

1.遇到互补可延长，延长可得角相等.

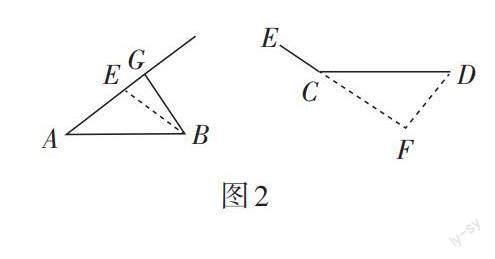
如图2，①已知相等的边和互补的角（即AB = CD，∠A + ∠ECD  = 180°），把AB和∠A所在的三角形△ABE作为目标三角形，∠ECD的CD边不动，延长EC，得到∠DCF = ∠A，即将“一边一互补角”转化为“一边一等角”，再以点D为顶点，作∠CDF = ∠ABE，则△CDF≌△ABE（ASA）.

2.遇到互补作等腰，等边等角都可得.

如图3，①已知相等的边和互补的角（即AB = CD，∠B + ∠C  = 180°）. 以AB为腰作等腰三角形ABF，AB = AF，可以证得AF = CD，∠AFE = ∠C，则△FAE≌△CDE（AAS） .

还可通过作双垂线构造全等三角形，如图4.

模型应用

例 如图5，在△ABC中，AB = AC，D为BC的中点，∠EDF = ∠B + ∠C，与边AB，AC交于E，F两点. 求证：DE = DF.

学法指导1：抓住已知条件BD = CD，∠B = ∠C，在CA上截取CG = BE，连接DG，如图6，可使△BDE≌△CDG，得到DG = DE，再证DF = DG，等量代换可得DE = DF.也可以在BA上截取BG = CF，证明同理.

學法指导2：连接AD，根据等腰三角形三线合一，AD平分∠BAC，即∠BAD = ∠CAD，把AD当成相等的边，如图7，在AB上截取AG = AF，证得△AGD≌△AFD，再证△EDG是等腰三角形.也可以在AC上截取AM = AE，证明同理.

学法指导3：如图8，通过已知可得∠BAC与∠EDF互补，由“四边形内角和等于360°”得到∠AED与∠AFD互补，而这对互补角的一边就是要证明有相等关系的DE和DF.顺着其中一角的边的反向延长线去找，可得到∠BED = ∠AFD，结合所求边DE和DF，把DE所在的三角形作为目标三角形，以DF为边作∠FDG = ∠EDB，DG交CA的延长线于G，此时    △BDE和△GDF中已有两对角相等，则第三对角也相等，即∠B = ∠G，可得∠G = ∠C，所以DG = DC，进而可得DG = DB，从而△BDE≌△GDF，得出DE = DF.图9亦然.

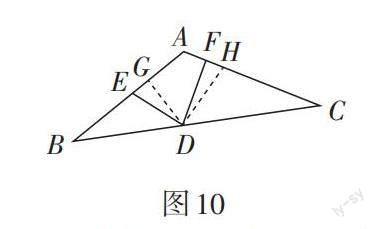
学法指导4：已知一边一角，还可以作特殊角构造全等三角形，例如90°角，如图10，过点D向AB，AC作垂线，垂足分别为G，H.

（作者单位：大连市第七十一中学）