结合Marchenko聚焦的非线性最小平方基准面延拓方法

2023-11-04 12:09朱峰程玖兵

地球物理学报 2023年11期

朱峰, 程玖兵

同济大学海洋地质国家重点实验室, 上海 200092

0 引言

地震勘探一般在地表或海面附近激发、接收地震信号.源自深部的反射或背向散射信号会受到地面/海表、上覆介质和观测系统的复杂影响,具体包括海面或地表相关的自由表面多次波干扰、观测面起伏或表层横向变速造成的运动学畸变、不规则岩体(如火成岩、盐丘与煤层等)引起的多次散射、障碍物(如钻井平台、湖泊等)或禁采区导致的非规则采样等.这些线性或非线性效应严重降低了深部有效信号的质量,给后续速度建模和偏移成像带来挑战.

基准面延拓旨在由地表真实观测数据重构基准面上的虚拟观测数据,从而克服上覆介质和观测因素对反射地震数据的影响.按照是否依赖地下速度模型,基准面延拓分为模型驱动和数据驱动两类方法(Schuster and Zhou, 2006).模型驱动的基准面延拓根据地下宏观速度并利用Kirchhoff积分、单程波或双程波延拓算子依次把检波器和炮点校正到基准面上,获得虚拟观测的地震数据(Berryhill, 1979; Reshef, 1991).它主要被用于消除起伏地表影响(杨锴等, 2007; 卢回忆等, 2010),数据规则化(Ferguson and Fomel, 2005)、改善异常地质体之下的波场照明和构造成像(Dong et al., 2009)等.当层间多次波等非线性波场效应较强时,这类方法需要提供精确的地下速度结构用于模拟全波场响应,以实现严格的波场延拓(Mulder, 2005).由于波场传播物理假设和观测条件限制,构建精确的速度模型十分困难,因而阻碍了模型驱动类的基准面延拓方法有效应对非线性波场效应(Planès et al., 2018).

数据驱动的基准面延拓方法不依赖于速度模型.基于井中或海底观测数据携带的格林函数信息,以地震干涉为核心的虚源法(Bakulin and Calvert, 2006; Schuster, 2009)通过多维互相关把实际检波器转化成虚拟震源,进而消除波场在上覆介质中的传播过程.当上覆介质存在强阻抗界面或复杂地质体时,波场会发生多次散射.由于观测数据携带的格林函数包含全波场信息,虚源法可自动考虑上覆介质中的非线性波场效应.然而,由于观测系统不完备(即不在封闭面上充分、规则地采集信号)和子波带限效应,干涉法重构的虚拟数据仅是目标信号的模糊化近似,在不同程度上受到了同非物理路径和观测孔径限制相关的假信号污染(朱峰和程玖兵, 2022).更重要的是,当检波器布设面与基准面不重合时,如果没有宏观速度模型等必要的先验信息,很难从实际观测数据获得干涉法需要的上、下行波格林函数.这很大程度上限制了虚源法的应用领域.幸运的是,随着解决一维介质单边逆散射问题的Marchenko方程(Marchenko, 1955)在本世纪以来受到地球物理界越来越多的关注,由地表观测的反射地震数据估计观测面与地下介质中任意点之间的格林函数场形成了比较坚实的理论基础(Rose, 2001; Broggini and Snieder, 2012; Wapenaar et al., 2014a).利用上覆介质宏观速度模型计算的直达波聚焦函数,Marchenko方法可以从地表观测的反射数据迭代估计地表到基准面的单向波格林函数(包含上覆介质中的多次散射等非线性效应),进而借助上、下行格林函数的多维反褶积(MDD)预测或衰减层间多次波(Wapenaar et al., 2012; van der Neut, 2012; Behura et al., 2014; Meles et al., 2016; Zhang et al., 2019; 匡伟康等, 2018; 孙红日等, 2021; 张乐乐等, 2022),或者实现考虑层间多次波的基准面延拓或地震成像(Wapenaar et al., 2014b; Ravasi, 2017; 靳中原等, 2017).不过,MDD涉及显式计算大量的点扩散函数和互相关函数,存储消耗非常大.本质上讲,Marchenko方法是由模型与数据联合驱动的.由于反射地震观测不完备和数据的带限效应,MDD面临的超大规模不适定问题求解起来很不稳定,而且对实际观测面上震源与检波器的分布有较严苛的要求(van der Neut and Herrmann, 2013).

在最小平方反演框架下实现基准面延拓,可在迭代过程中对虚拟观测数据施加恰当的约束或正则化处理,更好地压制采集脚印和非物理波场噪声的干扰.Ferguson(2006)最早将最小平方基准面延拓(LSR)用于数据规则化处理.接着,Xue和Schuster(2008)发现常规波动方程基准面延拓中因观测孔径限制引起的假信号可由LSR进行压制.针对模型驱动的LSR问题,为了改善数据拟合条件并尽可能剥离上覆介质的影响,Zhu和Cheng(2022)提出了同时反演上覆地层反射率和基准面虚拟观测数据的双参数LSR方法,并结合东海油气田应用实例展示了它在改善深层地震成像方面的潜力.最近,针对典型的海洋地震数据采集方式,朱峰和程玖兵(2022),朱峰等(2023)提出了基于数据驱动LSR压制表面多次波的新方法.

针对检波器布设面与基准面不一致而且上覆介质中发育较强层间多次波的复杂情况,本文拟把Marchenko与LSR方法相结合,建立可自动处理层间多次波的非线性基准面延拓方法.

1 方法原理

1.1 基准面到地表的波场转化方程

正问题的建立是求解反问题的前提.波场互易定理(Haines, 1988)描述了地下任意两个水平无限延伸界面上波场之间满足的积分恒等关系,为建立不同深度界面上波场相互转化方程提供了理论依据.它既被用于构建基准面上虚拟观测数据到单向格林函数的正演方程,又支撑Marchenko方法以聚焦函数为桥梁从地面观测反射信号迭代估计基准面上的单向波格林函数.

假定存在两个相互独立的波场状态A和B,它们在两个水平无限延伸边界Λi和Λj包围的封闭区域内部介质完全相同且无震源分布(封闭区域外介质特性和震源分布无要求),则两个边界上的单向波场在频率域满足以下卷积型波场互易定理(Wapenaar et al., 2004):

(1)

和相关型波场互易定理:

(2)

其中xi和xj分别是边界Λi和Λj上的水平坐标,P代表边界上的通量归一化单向波场(上标“+”和“-”分别表示下行波和上行波,下标“A”和“B”分别代表上述两种波场状态,上标“*”表示对频率域复数波场取共轭,对应时间域的波场翻转).注意,相关型互易定理要求封闭区域内无非弹性能量耗散.

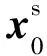
表1 下伏介质封闭区域边界上单向波场的汇总表Table 1 One-way wavefield variables on the boundaries of an enclosed domain beneath the datum

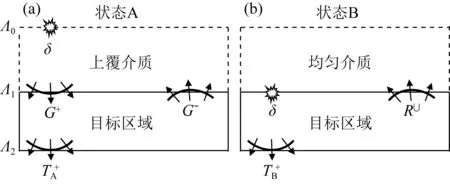
图1 以基准面下伏介质为封闭区域的波场状态示意图Fig.1 Schematic diagram of the wavefield states in an enclosed domain beneath the datum

将表1中的波场代入(1)式所示的卷积型互易定理,整理后得到:

(3)

该式给出了虚拟观测数据和基准面上的上、下行格林函数之间的关系.当基准面上恰好布设了足够多的多分量检波器,如拖缆双检、VSP、海底电缆(OBC)或海底节点(OBN)观测,则可通过观测数据的声压分量与质点垂直振动速度(即P/Z)叠加/相减分离出上、下行波场(Amundsen et al., 2000; 刘学义等, 2021).本文着重考虑检波器布设面与基准面不重合、上覆介质存在层间多次波等非线性波场效应的情况,此时基准面上单向波格林函数的估计就成为了核心问题.

1.2 重构格林函数的Marchenko聚焦方法

表2 封闭上覆介质边界上的单向波场汇总表Table 2 One-way wavefields on the boundary of the enclosed overburden media

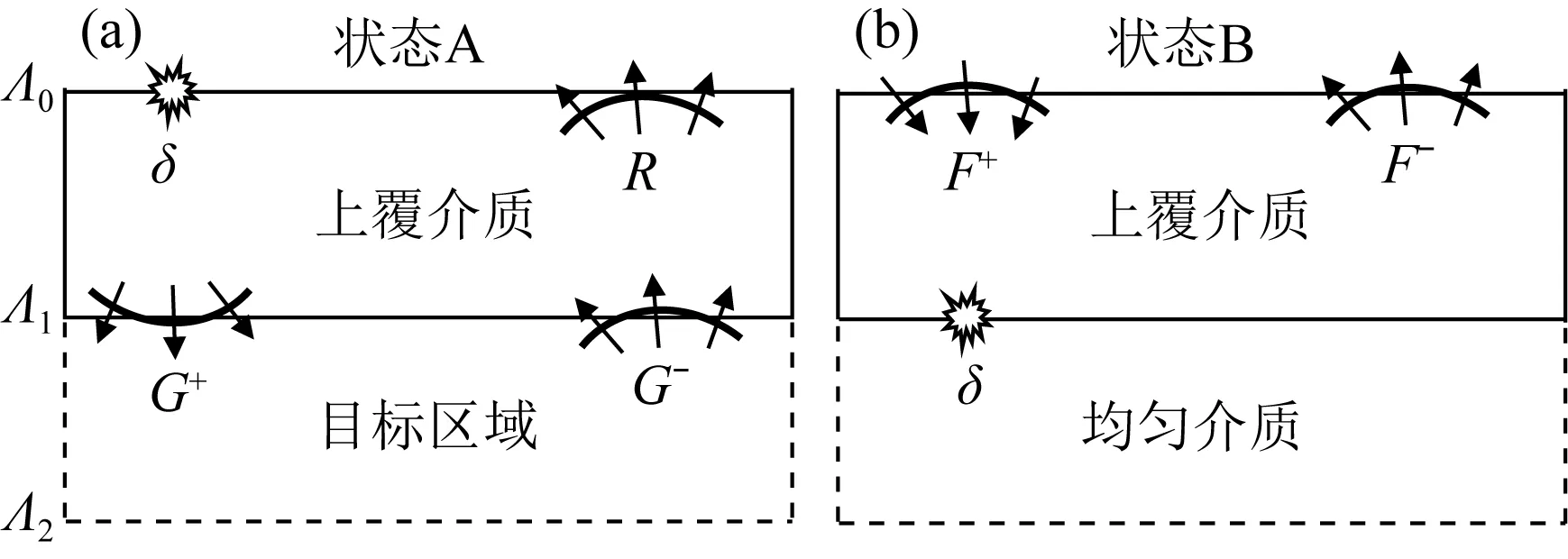
图2 以上覆介质为封闭区域的波场状态示意图Fig.2 Schematic diagram of the wavefields in the enclosed overburden media

(4)

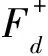
方程组(4)含有四个未知变量(即F+、F-、G+和G-),无法直接求解.这里采用Broggini和Snieder(2012)以及Wapenaar等(2014a)提出的迭代求解方法(见附录A).基本思路如下,将下行波聚焦函数、格林函数分别拆分成直达波和尾波两种成分,其中下行直达波聚焦函数可依据已知的上覆介质宏观速度模型正演模拟出来.利用聚焦函数与格林函数在时间分布区间上的差异,可将方程组(4)转化成仅含下行聚焦函数尾波和上行聚焦函数两个待求变量的迭代求解公式.把迭代估计的聚焦函数代入Marchenko方程组并考虑格林函数在时间轴上的分布区间,就可以重构出地表到基准面的上、下行波格林函数.

1.3 基于Marchenko聚焦的最小平方基准面延拓

根据前文推导,从基准面虚拟观测数据到上行波格林函数的正演方程可写成矩阵形式:

G-=G+R∪.

(5)

这表明,基准面上的下行格林函数G+与虚拟反射数据R∪经多维褶积运算,能够合成有更长波路径的上行格林函数G-(如图3).注意,下行格林函数不仅包含直达透射波(黑色路径),还含有在上覆介质中形成的层间多次波(红色路径)以及经过下伏介质的层间多次波(紫色路径)等非线性波场效应.尽管(5)式可以考虑高阶多次散射,但为了简洁起见,图中仅展示了一阶层间多次散射.

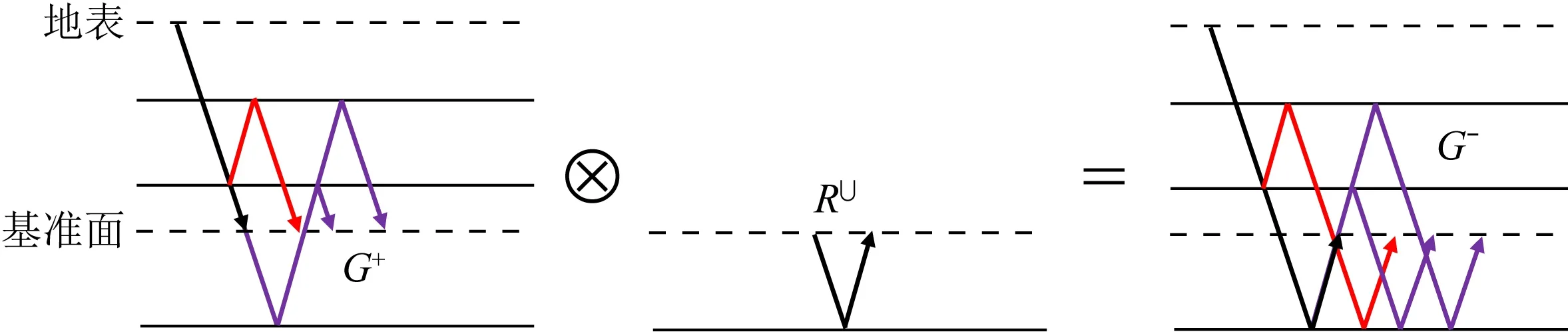
图3 多维褶积正演示意图Fig.3 Schematic diagram of forward modeling by multidimensional convolution

基准面延拓对应(5)式的逆过程,故有:

R∪=[G+]-1G-.

(6)

(6)式表示多维反褶积(MDD)运算.由于直接构建下行格林函数的稀疏矩阵并求逆非常困难,通常把MDD转化为如下求解公式:

(7)

其中G+*G-和G+*G+分别对应互相关函数和点扩算函数的集合(van der Neut,2012).如果按前文Marchenko方法构建单向波格林函数,则(6)或(7)式就是基于MDD的Marchenko基准面延拓方法(Wapenaar et al., 2014b).

Marchenko基准面延拓在实际应用中面临一系列挑战.首先,对于常规反射地震观测系统而言,观测孔径有限且炮点、检波器空间位置不重合,MDD隐含的地震干涉过程不足以消除基准面上覆介质中波场效应的影响,估算的虚拟观测数据存在相干的假信号.其次,多维互相关函数或点扩散函数集合对应的矩阵规模为2×Nw×(Ns×Nr)2,其中Nω、Ns和Nr分别是频率采样、炮点和检波点个数.对于典型反射地震观测系统(取Nω≈50,二维情况下Ns=Nr≈1000,三维情况下Ns=Nr≈1000×1000),以单精度浮点类型进行数据存储时,这些矩阵的理论存储消耗可达400TB(二维)和4×108TB(三维),对现有的计算机硬件条件构成极大挑战.而且,这种超大规模MDD运算也很不稳定(van der Neut and Herrmann, 2013).

为了避免显式计算与操作多维互相关函数和点扩散函数,同时方便对估计的虚拟观测数据施加恰当的正则化处理(以减少Marchenko基准面延拓中的假信号干扰),在最小平方反演理论框架下求解(6)式代表的反问题.于是,构建如下目标函数:

(8)

等式右边包含基于L2范数的数据拟合项和基于L1范数的模型(即虚拟观测数据)正则化处理或约束优化项,其中ε为权重因子.

方程(8)采用梯度类的局部优化迭代算法进行求解:

(9)

其中k表示迭代次数,α表示步长,gk代表泛函梯度,其表达式可由伴随状态法(Plessix, 2006; 朱峰和程玖兵, 2022)推导得到:

(10)

(10)式中δG-=G+R∪-G-表示模拟与Marchenko方法估计的上行格林函数之间的残差.带正则化处理的迭代算法可参照朱峰和程玖兵(2022).对于最小平方基准面延拓(LSR)方法,存储消耗量级约为4×Nt×Ns×Nr(其中Nt是时间采样点数),主要包括上、下行格林函数、泛函梯度以及虚拟观测数据.这种最小平方反演算法的存储规模远小于基于MDD的算法.

1.4 算法流程

根据上述方法原理,基于Marchenko聚焦的非线性LSR方法的实现可归纳为如图4所示的三步流程:首先估计聚焦函数,即根据上覆介质宏观速度模型正演模拟透射直达波,以它和反子波(如脉冲反褶积)的地表反射数据作为输入,按附录A中公式(A9)迭代估算上、下行聚焦函数.然后基于它们和地表反射脉冲响应数据按公式(A10)重构基准面上的上、下行格林函数(场).对于这些单向波格林函数而言,震源仍然在地表,但检波器已经延拓(沉降)到了基准面.最后将上、下行格林函数代入约束优化LSR反演算法,最终输出炮点、检波器均分布在基准面上的虚拟观测数据.

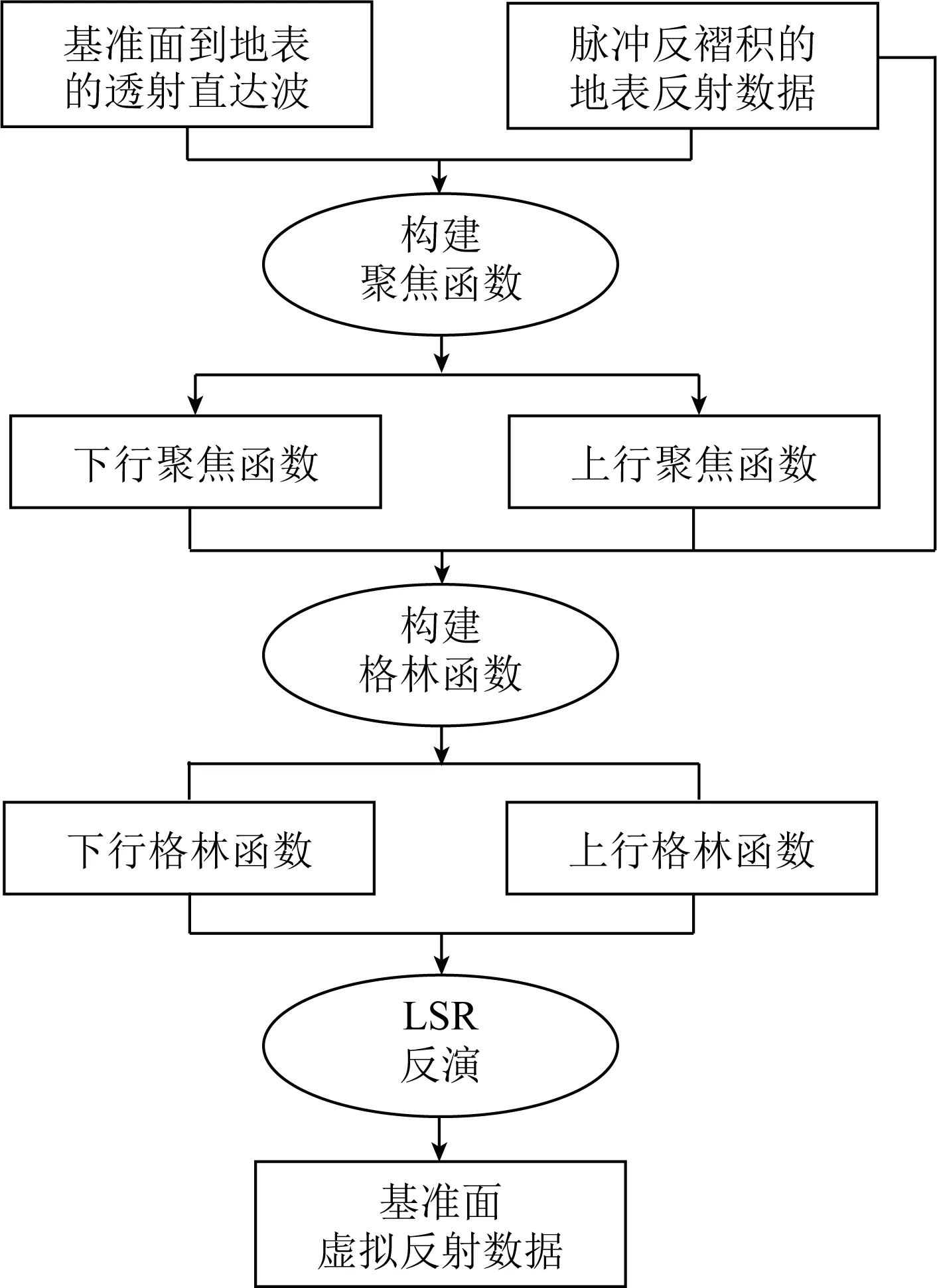
图4 基于Marchenko聚焦的最小平方基准面延拓算法流程Fig.4 Workflow of least-squares redatuming based on Marchenko focusing

2 数值实验

本部分通过两个合成数据实验检验非线性LSR方法的有效性.第一,通过含低速夹层的水平层状模型算例展示处理流程关键步骤的结果,结合波路径分析以及与参考答案的比较揭示方法的工作机制.第二,利用高速透镜体模型算例考察本文方法对于上覆介质强多次散射的适用性.为了避免脉冲反褶积处理,这里在基于全波场模拟方法(Berkhout,2014)正演在地表观测的反射地震数据时,直接采用带通Ormsby子波(图5a和5b).

图5 用于合成脉冲反射数据的Ormsby子波(a) 波形; (b) 振幅谱图.Fig.5 The Ormsby wavelet used to simulate impulsive reflected data(a) Waveform; (b) Amplitude spectrum.

2.1 含低速夹层的水平层状模型

在如图6a所示的层状模型中,101个炮点和检波器被均匀布设在地表,基准面设定在500 m深处(白色虚线位置).图6b展示了由真实速度场光滑得到的基准面上覆宏观速度模型,用于正演直达透射波数据以近似下行聚焦函数的直达波成分(图7a).由于上覆介质含有低速夹层,波场模拟结果中除了含一次反射波,还含有层间多次波(图7b).为了便于观察,图7c显示了将层间多次波振幅增益10倍后的结果以及其中4个能量最强的一阶层间多次波对应的波路径.

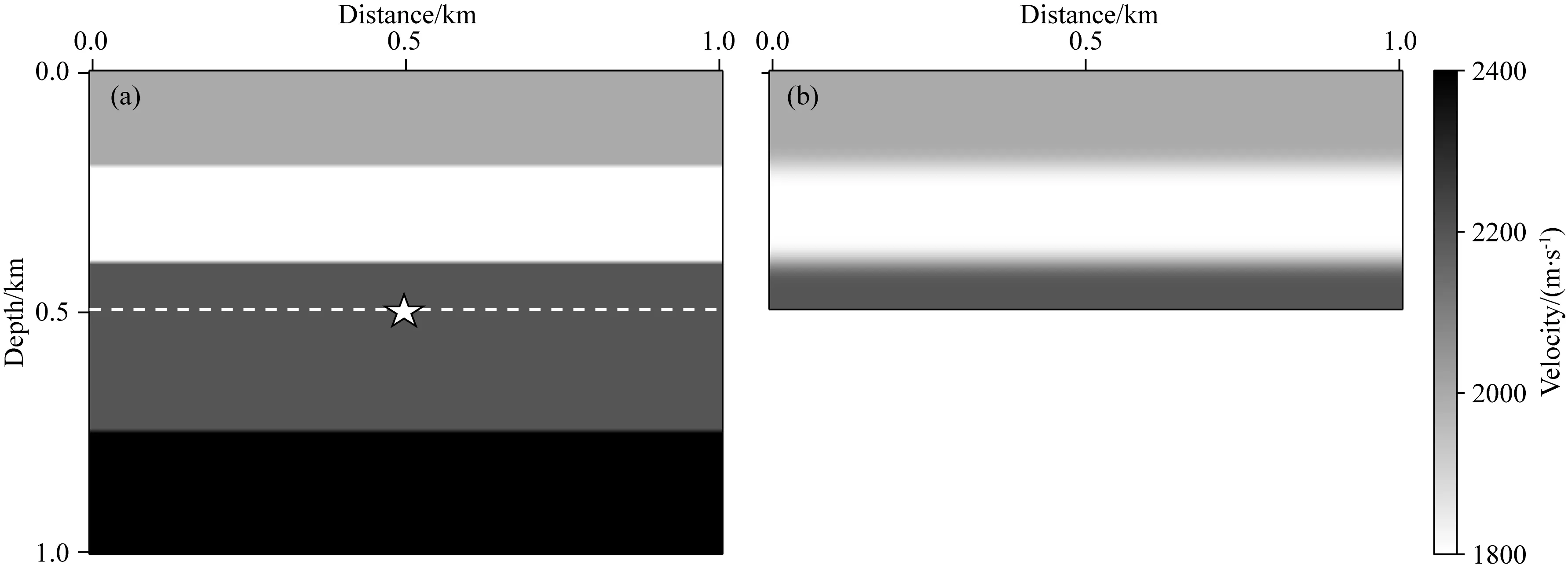
图6 含低速夹层的水平层状模型(a) 准确速度场; (b) 上覆宏观速度场. 图a中五角星指示了聚焦点位置.Fig.6 The layered model with a low speed interlayer(a) True velocity model; (b) Overlying macro velocity model. In figure a, the pentagram indicates the focusing point.

图7 用于Marchenko迭代的输入数据(a) 聚焦点到地表的透射直达波; (b) 震源位于地表0.5 km的反射数据; (c) 层间多次波及主要同相轴波路径.Fig.7 The input data for the Marchenko method(a) Transmitted primary wave from the focusing point to the surface; (b) Impulsive reflected data for sources at 0.5km on the surface; (c) Internal multiples and wave paths of the main events.

由Marchenko方法构建格林函数共分为两步,第一步,计算聚焦函数.将透射直达波和地表反射数据代入时窗约束的Marchenko方程((A9)式),迭代10次后得到上、下行聚焦函数(图8).在下行聚焦函数(图8a)中有两个同相轴,其中标号1是直达波成分,其波路径(图8c)与透射直达波(图7a)相同但走时相反;标号2是数值尾波,它和直达波成分极性相反且走时差是低速地层的双程走时,这样的时空特征保证了它刚好能够抵消低速地层顶界面的下行反射作用(图8c标号5),从而压制上覆介质层间多次波.如图8b和8c所示,下行聚焦函数经上覆介质一次反射后形成上行聚焦函数.第二步通过聚焦函数实现检波点端波场聚焦((A10)式),从而得到地表激发、基准面接收的上、下行格林函数(图9).图9b展示了下行格林函数及其波路经,其中能量占主导的是透射直达波(标号1)以及一阶层间多次相关的尾波(标号2-4).下行格林函数经过深部地层界面背向反射后形成上行格林函数(图9d).与同样用全波场模拟算法在基准面上以横向0.5 km的聚焦点为震源另外合成的地表参考数据(图9a和9c)相比,本文Marchenko算法估计的格林函数和它们相同.这里,上行格林函数波路径的前面部分与其对应的下行格林函数的波路径一致(图9b和9d),这部分会在后续多维互相关运算中被消去.

图8 横向0.5 km处的聚焦函数(a)下行和(b)上行聚焦函数以及它们的(c)波路径. 图c中点线表示对频率域波场取共轭或时间域波场翻转, 在物理上解释为由负时刻开始传播的非因果波场.Fig.8 Focusing functions at lateral 0.5 km Down-going (a) and up-going (b) focusing functions and their wave paths (c). The dotted line in Fig. c represents taking conjugate of the wavefield in frequency domain or flipping of the wavefield in time domain. It can be physically explained as non-causal wave which propagates from negative time.

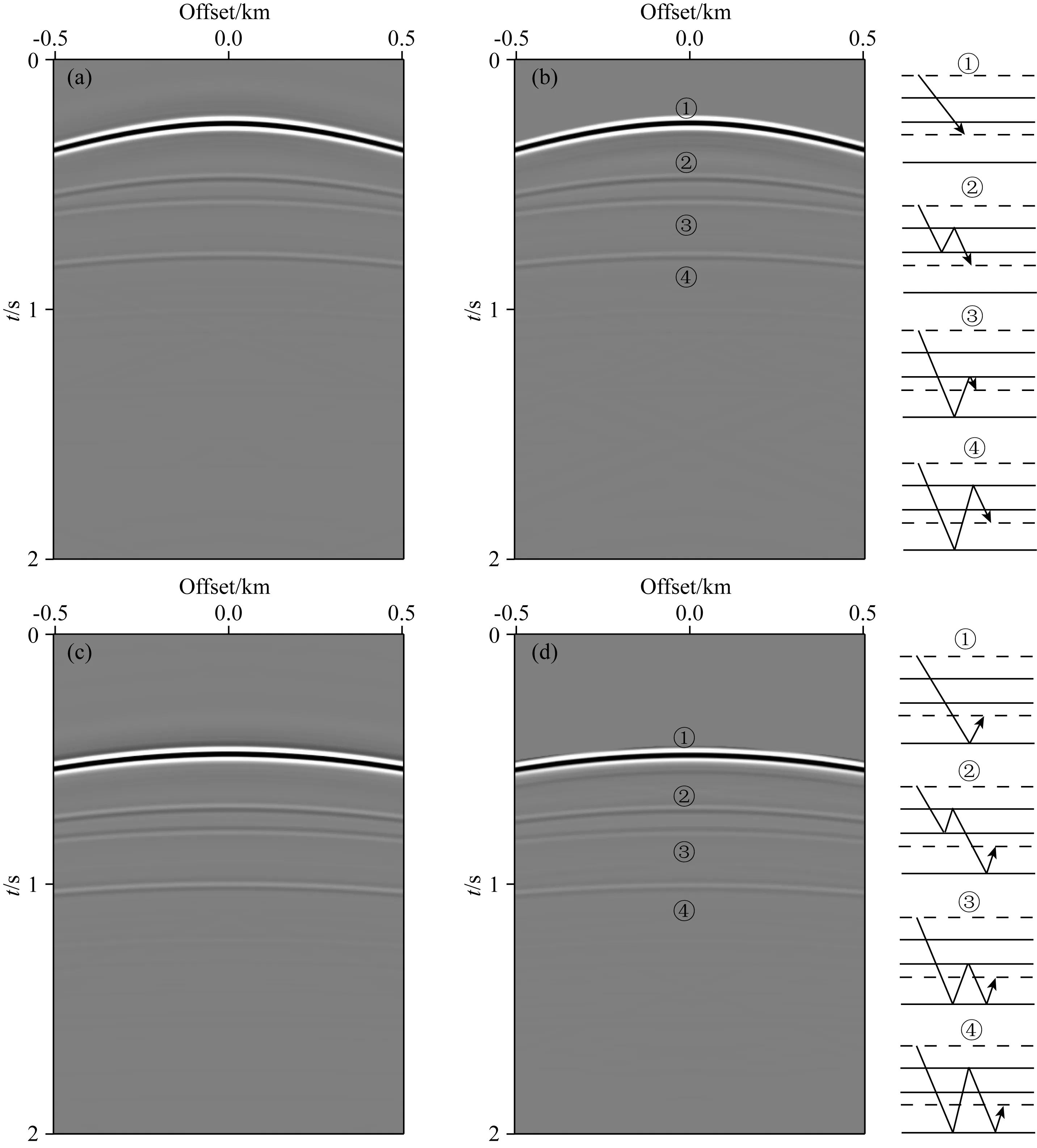
图9 横向0.5 km处的格林函数(a) 参考下行格林函数; (b) 重构的下行格林函数及其波路径; (c) 参考上行格林函数; (d) 重构的上行格林函数及其波路径.Fig.9 Green′s functions at lateral 0.5 km(a) Synthetic down-going Green′s functions for reference; (b) Constructed down-going Green′s functions and their wavepaths; (c) Synthetic up-going Green′s functions for reference; (d) Constructed up-going Green′s functions and their wavepaths.

利用估算的上、下行格林函数进行LSR处理.LSR第一轮迭代等同于基于地震干涉的虚源法(Bakulin and Calvert, 2006).在该过程中,多维互相关抵消了上、下行格林函数波路经的重叠部分,随后同相叠加的是有效的虚拟观测信号(图10b),而非同相叠加部分就形成沿非物理路径传播的串扰噪声(图10b白色箭头).如图10c,这些串扰会在LSR迭代30次后基本去除.然而,由于子波旁瓣压制不彻底,有效信号周围出现了平行的震荡噪声.通过施加稀疏约束正则化处理,震荡噪声得到压制,重构数据的分辨率也得到提升(图10d).

图10 震源位于基准面上横向0.5 km的虚拟反射数据(a) 参考数据; (b) 直接干涉数据; (c) LSR反演数据; (d) 稀疏约束LSR反演数据.Fig.10 Virtual reflected data with sources at 0.5 km on the datum(a) Reference data; (b) Direct interferometry data; (c) LSR data; (d) Sparse constrained LSR data.

2.2 高速透镜体模型

利用近地表强横向变速与高速透镜体复合模型合成数据测试算法对复杂地质情况的适用性.在图11a展示的速度模型上,采用固定排列观测系统在地表横向0～4 km范围均匀布设401个炮点和检波器,基准面设置在1.2 km深度(图中白色虚线位置).在基准面上的虚拟观测系统与地表实际观测系统保持一致.由于上覆介质存在强反差界面,在地表合成的炮记录中广泛发育层间多次波(图11b白色箭头).

图11 透镜体模型(a) 速度场; (b) 地表脉冲反射数据. 图a中五角星指示了聚焦点位置.Fig.11 The lens model(a) Velocity model; (b) Impulsive reflected data on the surface. In figure a, the pentagram indicates the focusing point.

图12a和12b展示了利用Marchenko方法经20次迭代构建的下行和上行聚焦函数.与简单模型算例(图8)相比,因上覆阻抗界面增多,聚焦函数同相轴也显著增加.这里的下行聚焦函数的数值尾波和直达波极性相同(图12a),这是由于随着深度增加,速度(阻抗)逐渐增大,上覆界面的下行反射系数为负,想要抵消它们产生的极性翻转的下行多次波,数值尾波的极性需与直达波一致.将聚焦函数代入(A10)式计算由地表到基准面的上、下行格林函数,其中下行格林函数(图12c)由上到下依次为透射直达波(黑色箭头)和层间多次震荡形成的尾波.如图12d,下行直达波和尾波经深部地层背向反射回到基准面分别形成上行格林函数的一次反射波(黑色箭头)和层间多次波.

图12 横向2 km处的聚焦函数和格林函数(a) 下行聚焦函数; (b) 上行聚焦函数; (c) 下行格林函数; (b) 上行格林函数.Fig.12 Focusing functions and Green′s functions at lateral 2 kmDown-going (a) and up-going (b) focusing functions; Down-going (c) and up-going (d) Green′s functions.

格林函数直接干涉重构的虚拟数据含有明显的非物理路径串扰噪声(图13a),经稀疏约束LSR迭代30次后进行了有效压制(图13b).此外,LSR还抵消了上、下行格林函数中的子波信息,重构出来自基准面以下的脉冲反射响应.为了方便对比,在虚拟数据上褶积了主频20Hz的雷克子波(图13c),并抽取了零偏移距剖面(图14).在地表观测的反射数据中(图14a),透镜体顶底界面相关的层间多次波(白色箭头)与深部有效信号(黑色箭头)混叠在一起,不利于深部构造解释.如图14b所示,虚源法校正了高速透镜体对深部反射的扭曲,但也产生了许多串扰噪声.通过LSR处理,这些噪声得到有效压制(图14c).MDD(Thorbecke et al., 2017)的基准面延拓结果(图13d和图14d)同样具有压制层间多次波串扰和反子波效果.然而,由于频率域数据矩阵运算难以施加预条件和正则化处理,即便采用了大型稀疏矩阵的稳定求解算法(LSQR),反演结果中仍残留有部分噪声和干扰.

图13 基准面反演的虚拟数据(a) 直接干涉重构数据; (b) LSR反演数据; (c) 褶积雷克子波后的LSR反演数据; (d) MDD反演数据.Fig.13 Inverted virtual data on the datum(a) Direct interferometry data; (b) LSR data; (c) LSR data convolved with Ricker wavelet; (d) MDD data.

图14 零偏移距剖面(a) 地表反射数据; (b) 直接干涉重构数据; (c) LSR反演数据; (d) MDD 反演数据.Fig.14 Zero offset profiles(a) Surface reflected data; (b) Direct interferometry data; (c) LSR data; (d) MDD data.

3 结论与讨论

针对检波器布设面与基准面不重合且上覆介质存在强非线性波场效应的情况,本文构建了基于Marchenko聚焦的非线性最小平方基准面延拓方法.它以聚焦函数为桥梁,由地表反射数据估计格林函数,进而通过约束优化的LSR方法反演虚拟数据.相比于基于MDD的Marchenko基准面延拓方法,LSR一方面避免了庞大的点扩散和互相关函数集合的显式计算、存储,以及大规模稀疏矩阵的不稳定求逆;另一方面,通过对虚拟数据施加L1范数正则化,有效的压制了非物理路径串扰噪声以及观测孔径和子波带限的不利影响,在实现压制层间多次波的同时,重构了在基准面上虚拟观测的高分辨率反射数据,为面向深部目标的成像奠定了良好的基础.

本文方法在实际应用时还面临如下问题:首先,上、下行格林函数的估计依赖于运动学准确的透射直达波场,当上覆宏观速度模型存在较大误差时,会导致重构的虚拟数据不准确;其次,Marchenko迭代要求输入反子波的地表单位脉冲响应,这就需要对每一炮数据预先估计震源子波,并通过反褶积对其加以消除;最后,经典的Marchenko方法要求输入的观测数据满足炮检点耦合,如何摆脱这一限制仍然是当前的研究热点(Ravasi, 2017).上述挑战将在今后的研究中加以考虑.

致谢感谢王腾飞、邹鹏和武泗海等在本文研究过程中提供的建议.

附录A 利用Marchenko聚焦求解单向波格林函数

由正文可知,基于波场互易定理推导的单边格林函数表示定理满足:

(A1)

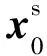
参照Broggini和Snieder(2012)以及Wapenaar等(2014a),把下行波聚焦函数和格林函数拆分为直达波与尾波,即:

(A2)