稳态随机激励下结构阻尼系统的拓扑优化方法

刘伟佳，赵旭奇

结构拓扑优化是在设计领域内找到形状配置和材料分布的设计方法.各类拓扑优化方法已广泛应用于静载荷下的结构设计和实际工程问题［1-2］.在工程应用中，结构设计问题经常会遇到随机因素，如随机参数和材料特性、边界条件和外部载荷的不确定性［3-6］.其中一个关键课题是在稳态随机激励下的结构设计［7］.因此，本文介绍了一种基于虚拟激励法（PEM）［8］的大规模结构在稳态随机激励下的拓扑优化方法.该优化模型以宽频率区间内随机位移的功率谱密度（PSD）为目标函数.此外，还考虑了一类具有结构阻尼的线性动力系统及其在稳态随机激励下的结构响应.该方法结合频率响应计算［9］及随机响应的PEM 方法，以计算宽频率区间内的频域解.优化模型中目标函数的导数基于伴随方法得到，其中伴随向量同样可用本文方法求解.数值实验验证了本方法的高效性.

1 计算方法

外激励作用下，结构阻尼系统经有限元方法离散后的运动控制方程可以写成如下形式：

其中：M为系统的质量矩阵；为相应的刚度矩阵；η为材料的阻尼系数；(t)，X(t)为系统加速度及位移向量；B为n×d维随机激励定位向量；f(t)为d维稳态随机激励向量，其功率谱（SPD）矩阵为Sf.

基于PEM［8］，输入与输出的SPD 矩阵及有如下关系：

其中：为H的共轭矩阵，H(ω)为复频率响应矩阵，且满足

因此，输入激励f(t)的SPD 矩阵Sf为非负定Hermite 矩阵且可分解为根据输入与输出SPD 矩阵之间的关系，可以得到：

由此，可利用PEM 将稳态随机激励分析转化为如下结构频率响应分析：

在每个代求频率点，对系数矩阵进行分解回代可得到响应的精确解.然而，对于大规模系统如此会产生巨大的计算量.模态叠加法通过将相应无阻尼系统的特征向量线性叠加得到结构响应，其精度随着模态数量的增加而提高.对于大规模结构无法求得所有特征向量，因此通过截断的方法构造如下虚拟频率响应向量u(ω)的形式：

其中：ΦL为已求得的无阻尼系统特征向量；ΦH为截断的无阻尼系统特征向量.结构响应的截断部分极大影响虚拟频率响应向量u(ω)的精度.

本文主要讨论引入方法高效计算截断部分w(ω)的近似解.考虑到结构模态关于矩阵M正交性关系，w(ω)满足如下形式：

下面将利用迭代的方法计算w(ω)，其表达形式可近似写成

其中：向量pi由如下迭代格式得到

并得到相应的系数a0及系数向量z(ω)，由于迭代格式的收敛性由谱半径决定.具体推导过程可参考文献［9］.

基于密度法的稳态随机激励下结构拓扑优化模型［10］可有：

其中：ρe为设计变量，其意义为单元e的密度；为了确保迭代过程中质量与刚度矩阵不出现奇异设置ρmin= 0.001；ve为单元e的体积，V0为设计区域的总体积，优化模型中的目标函数为考虑频段内某一自由度r的功率谱密度积分，且

在动力学拓扑优化过程中，由于设计变量的更新造成刚度与质量不匹配，导致系统出现局部模态的现象.基于这样的数值不稳定性，已有许多改善方案，在一定程度上解决了局部模态的现象.本文采用的是多项式插值方案［11］.

灵敏度分析假定外部激励与设计变量无关.本文选择伴随方法计算目标函数的灵敏度.对于设计变量数量较大的情况，该方法是优选的.它还可以避免计算特征向量导数，因为这在直接微分法中是一项困难的任务.具体推导过程可参考文献［12］.此外，基于密度方法的结构拓扑优化可能会遇到数值不稳定现象，如棋盘格和网格依赖性.网格过滤技术可以用来避免这些问题.最后，利用GCMMA算法作为优化问题的求解方法［13］.

2 数值实验

如图1 所示，考虑设计区域为1 m×0.5 m，厚度0.01 m 的矩形，结构左侧固定.利用有限元方法将该区域划分为200×100 个平面4 节点应力单元，系统包含40 400 自由度.体积约束为小于30%.结构左侧中点处沿y轴方向施加白噪声激励，其功率谱密度大小为104m2/Hz.杨氏模量E= 7 × 1010Pa，泊松比υ= 0.35，密度ρ= 2 700 kg/m3，结构阻尼系数η= 0.01.优化过程的收敛准则为相邻迭代步的目标函数相对误差小于10-4.目标函数为［0，300］Hz，［0，600］Hz 和［0，1 000］Hz 内荷载加载自由度PSD 值的积分.为了保证结构响应的计算效率，将迭代格式中的收敛准则设为10-6.

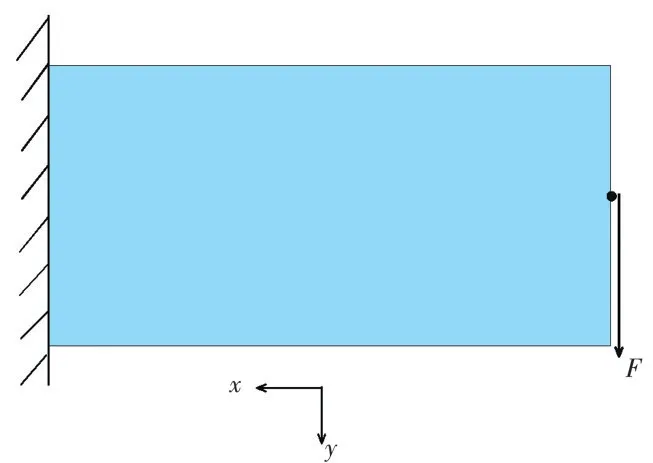
图1 二维悬臂梁

优化模型的初值选择是将所有的设计变量ρe均设置为0.3，相应结构的基频为93 Hz.基于本文所提出方法的总耗时及相应频段的初始、收敛的优化目标函数值见表1.

基于本文的拓扑优化方法，三个不同频段稳态随机激励下的优化结果如图2 所示.

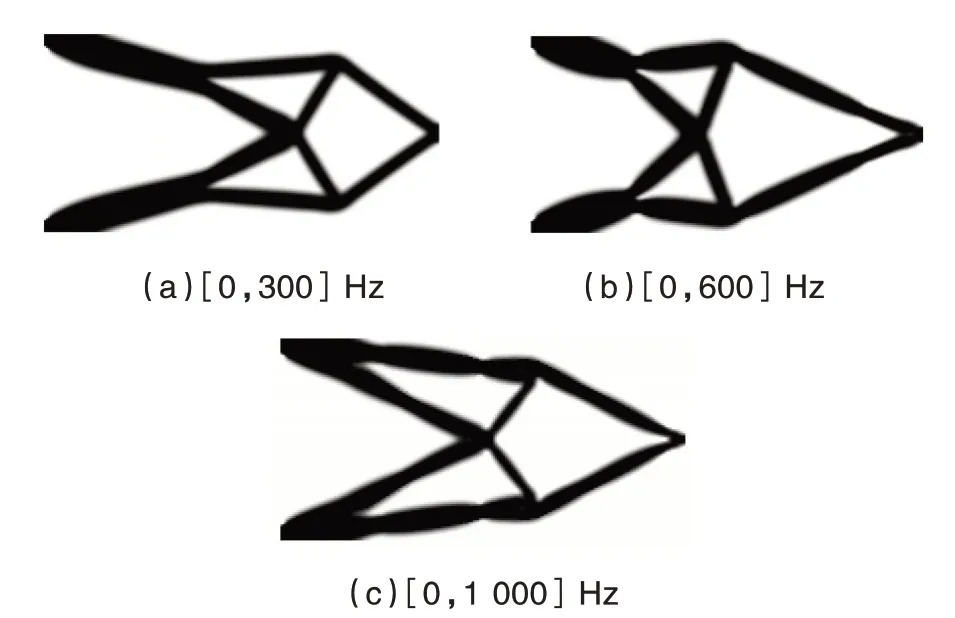
图2 各频段激励下的最优化设计

图2（a）~图2（c）中的优化结构的基频，分别为202.9 Hz、275.5 Hz、341.0 Hz.为了比较三个优化构型在各自考虑区间内的动力学性能，其荷载自由度在频段［0，1 000］Hz 的功率谱密度如图3 所示.可以发现，随着激励频段的扩大，优化结构的基频会随之增大，且动力学响应会极大地影响最终的优化构型.表2 列出了在各自频段激励下利用本文方法计算初始结构响应的CPU 时间具体分布.为了较好地评估本方法的精确性，计算结构响应的相对误差

表2 初始结构计算响应的CPU 时间分布

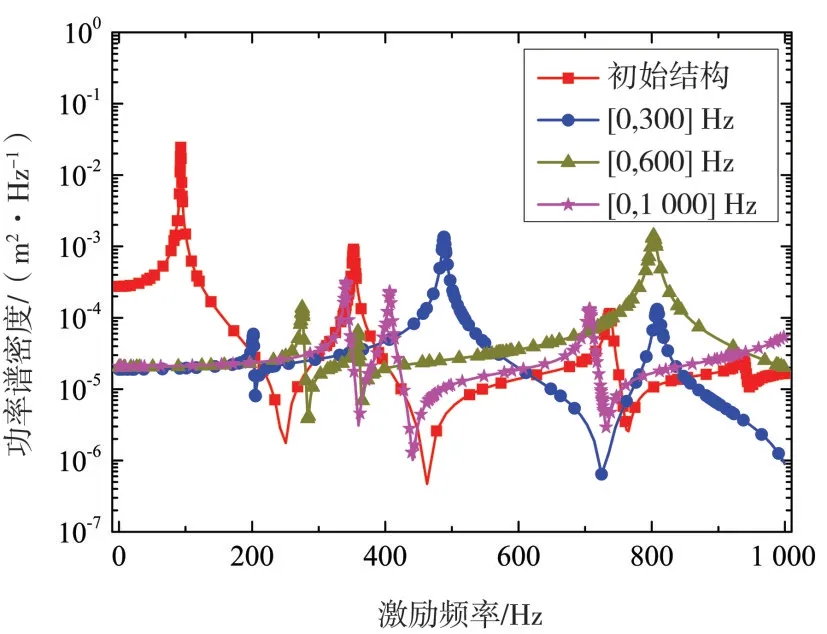
图3 初始结构与最优化设计的功率谱密度响应曲线

其误差曲线如图4 所示.由文献［9］中的推导可知，迭代格式的谱半径在频率区间的最右端ωR达到最大值.因此，截断模态部分中的向量pi可有最高激励频率自适应地确定，结构响应的表达式在整个频率间隔内都是有效的.这部分理论很好地验证了图4 的结果，初始结构响应向量的相对误差值在ωR达到最大且小于10-8.

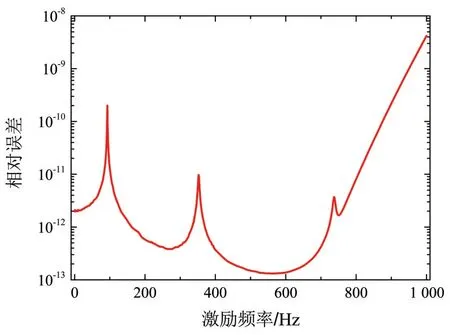
图4 基于本文方法的初始结构频率响应相对误差曲线

3 结语

本文提出了结构阻尼系统随机响应拓扑优化方法.与传统的拓扑优化方法相比，该方法具有更高的精度和适应性，主要体现在三个方面.第一，方法可以根据用户定义的迭代算法的收敛速度自适应地确定模态叠加中涉及的低阶模态.第二，可基于给定的容差误差计算结构响应.最后，能够在更新设计变量后自适应调整计算过程.迭代算法只需要很短的CPU 处理时间，并且只占用小部分存储空间，即使对于大规模的结构问题也同样有效.通过伴随方法，本方法也可以对目标函数进行灵敏度分析.数值实验验证了该方法的准确性和有效性.对于给定自由度下随机位移的PSD 最小化问题，基于本方法的拓扑优化过程，不仅提高了计算精度，而且显著减少了CPU 时间.