黄土地层雨水管道施工对既有下卧地铁变形的影响

孙皓, 赵森森, 赵文财, 牛方园

(1.西北大学城市与环境学院, 西安 710127; 2.同济大学土木工程学院, 上海 200092;3.长安大学公路学院, 西安 710064; 4.中建丝路建设投资有限公司, 西安 710000)

近年来,城市地下空间建设不断发展,越来越多的新建地下结构将位于既有地铁隧道上方,两者不可避免会产生近接工程问题。目前以西安、郑州等为代表的黄土地层和以上海、天津等为代表的软土地层均出现了在既有地铁结构上方进行施工的案例,地下结构施工过程中由于基坑开挖或顶管开挖改变了土体的应力场,使得地铁隧道产生变形,危害结构安全。因此深入研究下卧地铁隧道在上部土体开挖卸荷时的变形受力规律及影响因素对于地铁结构的安全具有重要的意义。

目前地下工程施工多采用明挖法修建[1],一些学者采用理论推导、数值分析、模型试验等方法深入研究了基坑开挖对下卧隧道的影响。理论方面目前主要采用两阶段应力法计算基坑开挖后下卧隧道的隆起量,不同的学者[2-4]针对不同的土体模型(弹性、黏弹性等)、地基模型(Winkler、Vlazov、Pasternak、Kerr)和梁模型(Euler-Bernoulli梁、Timoshenko)对该方法进行了研究和改进。文献[5-7]通过建立有限元模型分析下卧隧道变形受力规律,研究施工方式及加固措施对下卧隧道的影响,特别地,杨友彬等[8]依托昆明软土地区某基坑工程,分析了基坑预加固对地铁隧道变形受力的影响。张浩等[9]通过相似模型试验研究下卧隧道的变形受力规律。任印文[10]基于缩尺模型试验分析了基坑开挖深度对下卧既有地铁隧道力学性能的影响。刘波等[11]基于案例调研数据统计得到3类地层条件下基坑卸荷开挖对地铁隧道变形的影响特征。毕书琦等[12]分析了基坑开挖作用下下卧既有隧道结构的垂直变形和净空收敛变形,并验证了加固措施的有效性。对于顶管法顶进施工对既有隧道的影响研究,Liang等[13]设计离心实验,研究了既有管道受隧道开挖的影响,分析了地层损失率、管线埋深等对管道的附加应力和变形影响。魏刚等[14]基于相似理论,分析了顶管施工对既有盾构隧道的位移影响规律以及隧道弯矩变化情况。吴垠龙等[15]采用数值模拟和现场测试结合分析了矩形顶管施工时下卧地铁隧道结构的变形响应特征,同时动态模拟了顶管顶进施工时侧摩阻力对下卧隧道变形的影响特征。张治成等[16]依托杭州德胜路综合管廊工程,采用Plaxis3D建立三维模型,提出适用于顶管法的土体收缩率确定方法,通过土体收缩率模拟地层损失的影响。姜之阳等[17]借助FLAC3D有限差分软件模拟了双线矩形顶管施工对下卧既有地铁隧道变形影响特征,进一步分析了不同抗浮配重对地铁隧道变形的抑制效果。

综上可知,目前对基坑开挖或顶管开挖对下卧隧道变形受力影响研究多集中于深大基坑与盾构隧道,且多单独研究基坑开挖或者顶管法对下卧隧道的影响,对两者共同作用的研究较少。鉴于此,现依托西安市雨水管道工程(上跨既有地铁线),对比分析明挖法和顶管法施工时下卧隧道变形规律,通过正交试验,研究在基坑开挖和顶管开挖共同作用下下卧隧道隆起量的影响因素,以期达到指导施工的效果。

1 工程概况

所研究西安市雨水管道工程总长度约900 m,东西向敷设,敷设起点布置溢流井,位于西安地铁某区间右线隧道上方顶部,管道从溢流井引出后向东上跨该区间左线隧道后。受本项目雨水管道施工影响范围内的地铁隧道区间里程为DK17+124.0～DK17+153.0对应总长为29 m。如图1所示,右线隧道距溢流井底6.50 m,左线隧道B形断面拱顶埋深为10.24 m,距基底处理层6.30 m,C形断面拱顶埋深为9.55 m, 距基底处理层5.55 m。

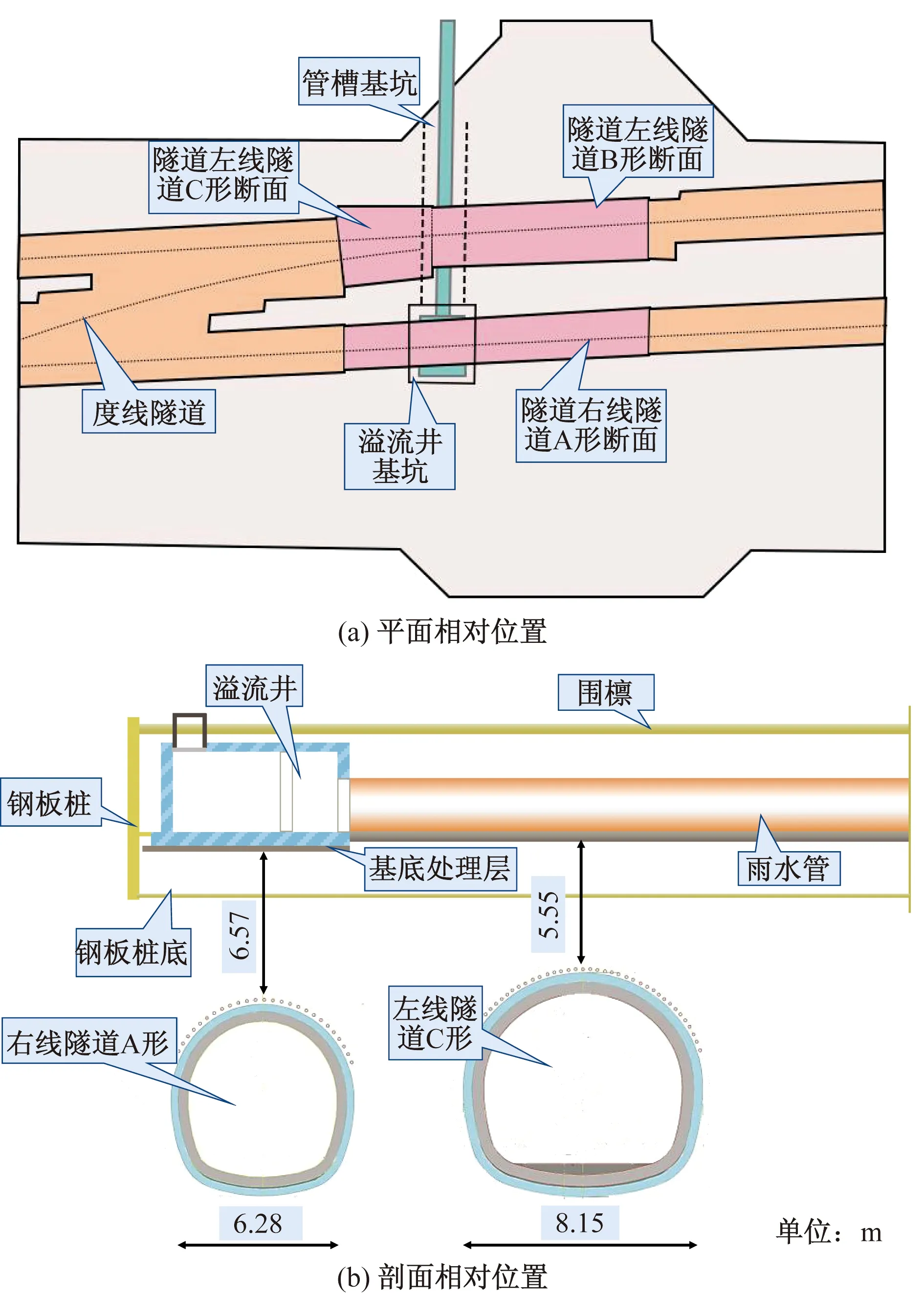
图1 管廊与地铁相对位置关系图Fig.1 Relative position diagram of pipe gallery and subway

雨水管道原方案采用明挖顺筑法施工,雨水管槽基坑宽度约3.7 m,开挖深度 4.0～4.1 m,溢流井位于地铁右线隧道上方,宽度约为6.9 m,长度约为7.4 m,开挖深度约为4.4 m,结合施工现场实际情况及工程水文地质条件,整条管线敷设路径上均采用钢板桩+型钢支撑等形式进行支护开挖。由于明挖顺筑法对地面交通影响较大,因此新方案采用顶管法施工,首先施作工作坑,然后进行挖土顶进,施工中为保证地层的稳定,第一条管道顶推施工完成后再施工第二条管道,顶管法现场施工如图2所示。

图2 顶管施工现场图Fig.2 Pipe-jacking construction

2 下卧地铁区间变形受力规律数值分析

2.1 数值模型建立

图3为数值计算模型,数值模型计算的范围为模型的四周及底部设置法向约束。在模拟顶管法施工过程中在管片和土体之间设置一层等厚的间隙单元,间隙单元的模量小于土体的模量,用以模拟顶管开挖后土体和管片贴合的过程。顶管管片、基坑围护、二衬采用shell63单元,钢支撑采用beam4单元,其余采用solid45单元。值得注意的是模型中左隧道为实际工程右线隧道,而模型中右隧道为实际工程左线隧道。

图3 数值计算模型Fig.3 Numerical calculation model

地层参数参考相关文献[18-19],土体共5层,采用D-P(Drucker-Prager)本构模型,具体参数如表1所示。

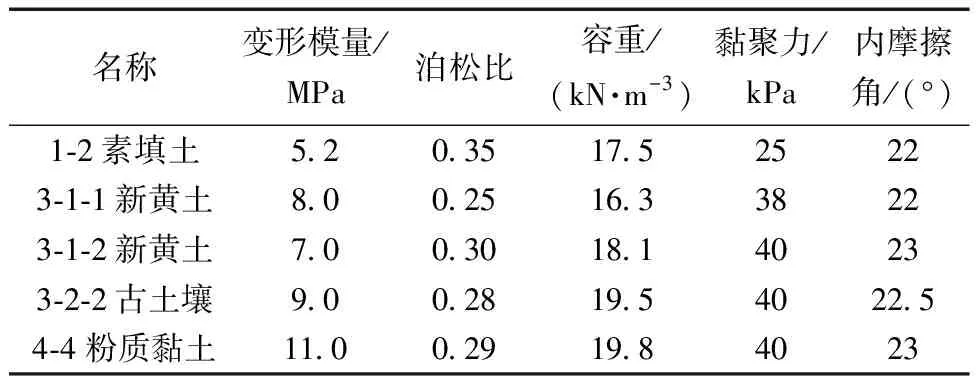
表1 土体材料参数

数值模拟流程为:第一步施加重力求解初始地应力,第二步开挖下卧隧道,激活初支和二衬。对于明挖法施工,第三步开挖溢流井基坑并激活钢板桩,第四步开挖管道基坑,激活钢板桩和钢支撑。对于顶管法施工,第三步开挖工作坑,第四步钝化顶管第一阶段土体、管片和间隙层单元,第五步施加顶推力,第六步钝化后一阶段土体、间隙层和管片单元,激活前一阶段管片和间隙层单元,循环进行第五、第六步直至顶管施工完成。为减少对土体的扰动,第一条顶管施工完后再施工第二条顶管。

2.2 明挖法数值模拟结果分析

如图4所示,基坑施工结束后,下卧隧道沿纵向竖向位移曲线两个反弯点距离约为5倍基坑宽度,该范围内隆起量较大,同时渗流井基坑与管道基坑相继开挖对下卧隧道的变形影响存在一定的叠加效应。渗流井基坑开挖后,左隧道结构拱顶位置受开挖卸荷影响较大,最大隆起量为2.89 mm;管道基坑开挖后,左隧道不同测点隆起量均大于1 mm,拱顶隆起量增至4.13 mm,右隧道结构整体受开挖卸荷影响较大,隧道结构整体隆起量约增大2 mm,拱顶隆起量由0.92 mm增至3.19 mm。

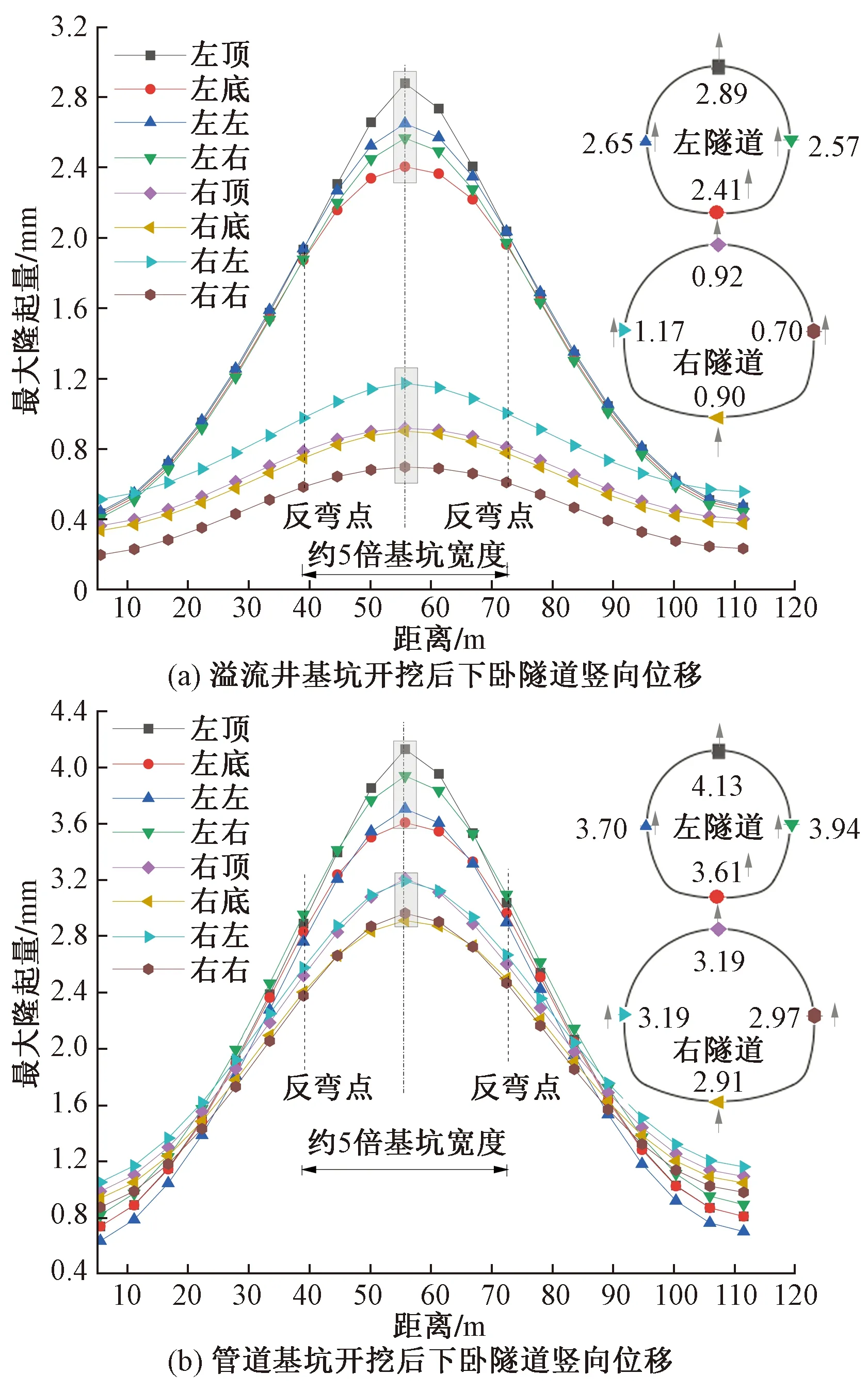
图4 明挖法施工地铁隧道竖向位移图Fig.4 Vertical displacement of subway under open-cut method

图5为明挖法施工时下卧地铁隧道的水平位移,可见下卧隧道水平位移与隆起量相比较小,约为隆起量的1/10,基坑正下方隧道水平收敛最大。以向右为正方向,溢流井基坑开挖后,左隧道左拱腰产生向右的水平位移,右拱腰发生向左的水平位移,说明左隧道断面发生了横向收缩,最大收敛值约为0.48 mm;右隧道整体向左移动约0.3 mm,断面基本没有横向收缩。管道基坑开挖后,左隧道整体向右移动,左隧道断面的收敛增加至0.55 mm,右隧道整体向右移动,断面发生横向收缩,最大收敛值为0.24 mm。由上述分析可知,说明管道基坑开挖后左隧道会发生扭转变形,右隧道断面发生竖向拉伸变形。

图5 明挖法施工地铁隧道水平位移图Fig.5 Horizontal displacement of subway under open-cut method

2.3 顶管法数值模拟结果分析

图6所示为采用顶管法施工时下卧隧道最大隆起量变化情况,施工步5～23步为第一条管道开挖过程,24～42步为第二条管道施工过程。对于左隧道,第一条管道刚开始开挖时,隆起量略有增加,随着顶管的推进,最大隆起量慢慢减少,同样第二条管道刚开始施工时隆起量增大,在第二条管道顶进过程中隆起量基本保持不变。总体来看,采用顶管法左隧道隆起量变化不大,增加约26.08%,左隧道在顶管刚开始施工时隆起量最大,最大为0.79 mm。右隧道在第一条管道顶进施工过程中,隆起量逐渐增大,顶管穿越隧道上方过程中隆起量增加最快,穿越隧道后隆起量基本保持不变;第二条管道顶管施工过程中,最大隆起量按相同的规律逐渐增大。整个过程中,隆起量增加约127.2%,最大隆起量为0.64 mm。

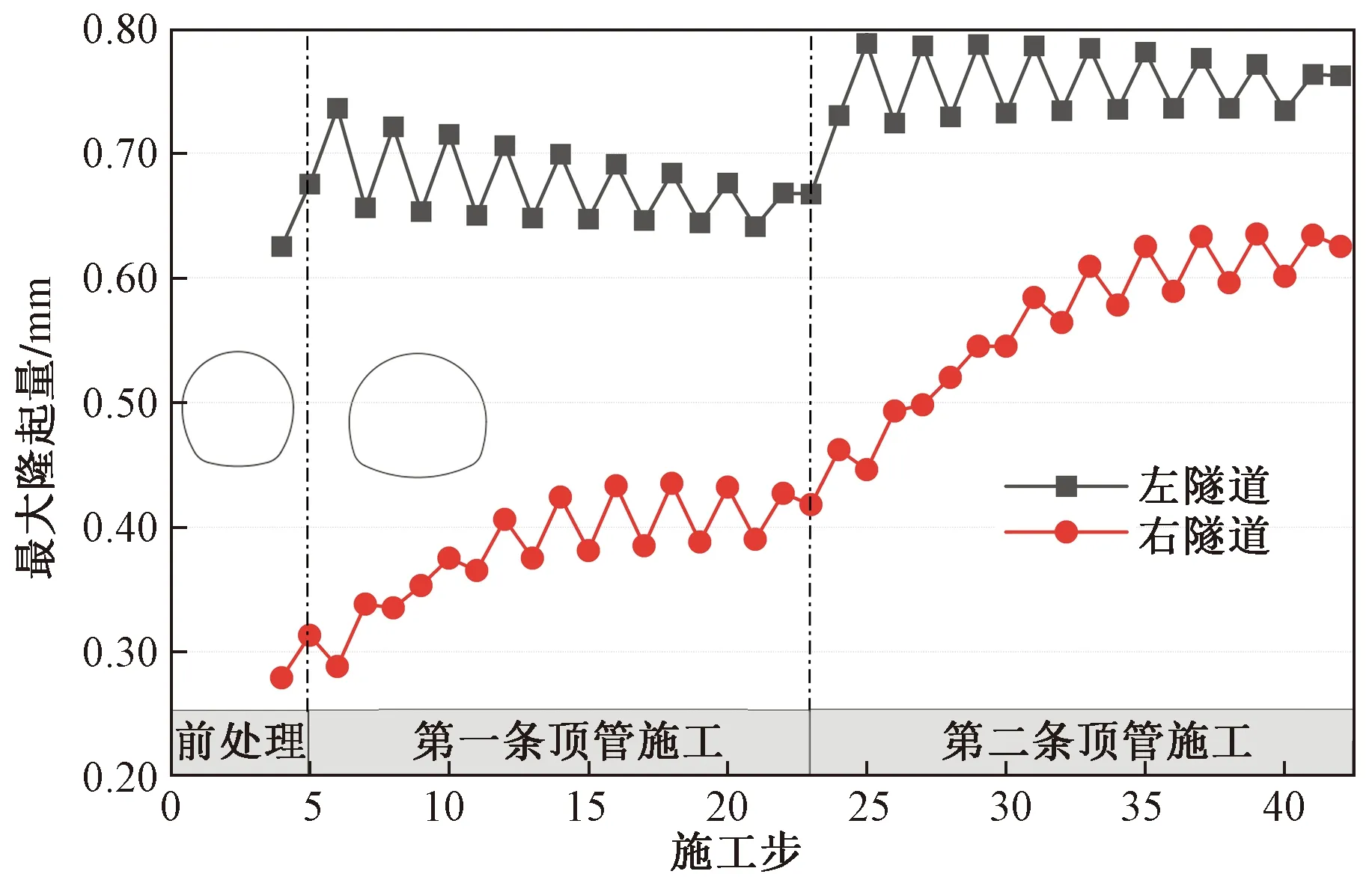
图6 顶管法施工隧道最大隆起量变化图Fig.6 Variation of maximum heave by pipejacking method

采用顶管法施工时,左右隧道均发生了向顶推力方向的位移,如图7所示,顶管正下方的水平位移最大,由于左隧道处于基坑正下方,产生了较大的横向收敛,最大为0.2 mm,右隧道的横向收敛较小,其横向位移产生的主要原因是顶推力的作用,当顶管穿越右隧道正上方时,拱顶约有0.14 mm的横向位移,拱底约有0.06 mm横向位移,说明右隧道有扭转的趋向,拱顶受到顶管施工的影响更大。

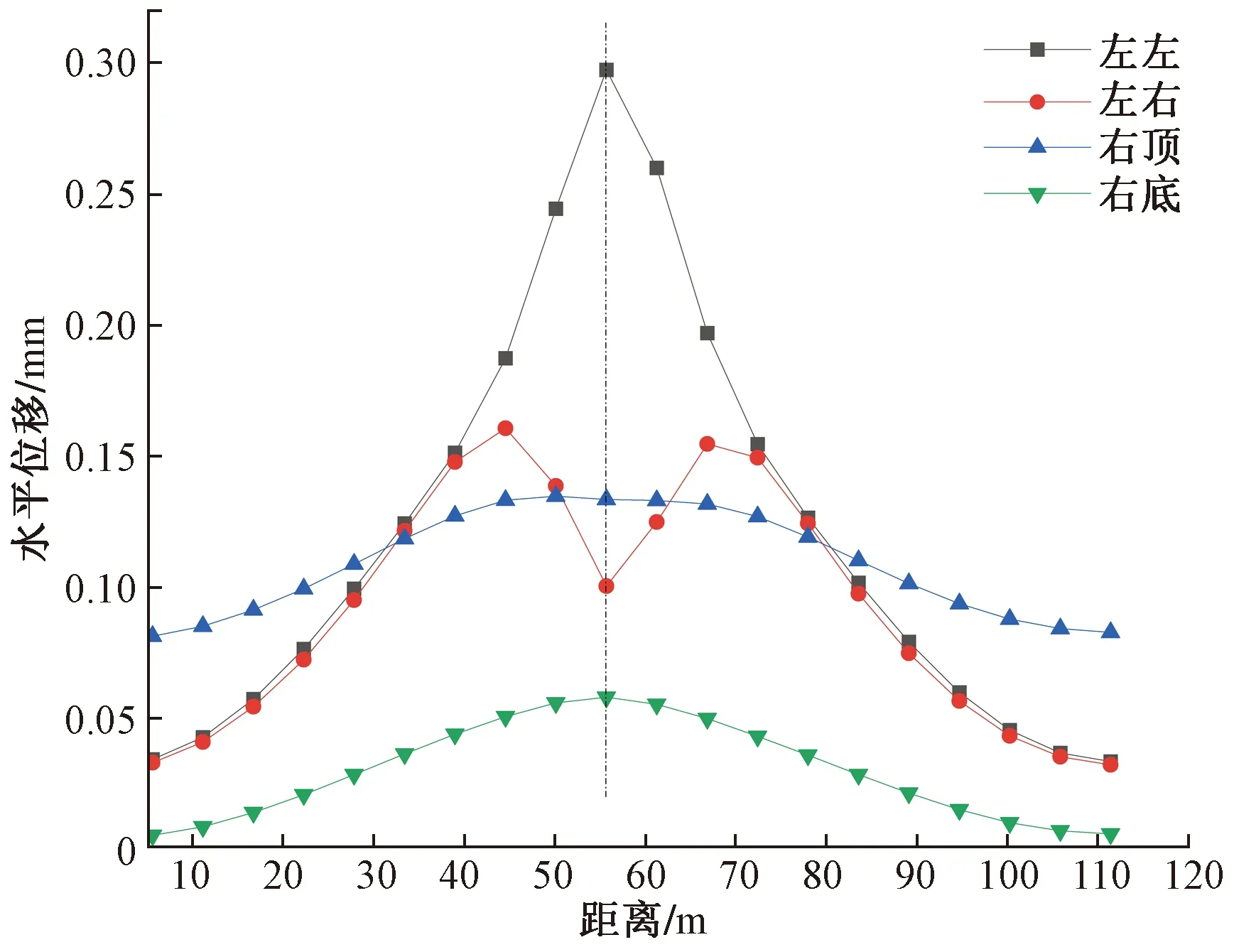
图7 顶管法施工下卧隧道水平位移变化图Fig.7 Subway horizontal displacement for pipe jacking method

2.4 实测数据分析

项目采用自动化监测法,左线(Z-121～Z-181)和右线(Y-116～Y-176)各设7个监测断面,每个断面布置7个监测点,拱顶和道床的3、4、7号监测点监测竖向位移,拱腰的1、2、5、6号监测点监测水平位移,测点布置图如图8所示。

图8 监测点布置图Fig.8 Monitoring point arrangement

随着施工的进行,左线隧道测点累计位移变化情况如图9所示,断面151距离顶管中心最近,发生的隆起量最大,顶管施工中隆起量最大为1.0 mm,图6所示有限元模拟结果为0.64 mm,比实测结果小,但相差不大,相应地断面151的横向收敛最大,最大达到1.7 mm,断面141处于左线隧道断面的突变处,收敛为负值,5月1—10日为顶管上穿左线隧道的时间段,在该段时间内断面横向收敛较大。

图9 左线隧道测点累计位移变化Fig.9 Cumulative displacement of monitoring points for left line

如图10所示为右线隧道测点累计位移变化情况,断面146处于溢流井下方,在4月9日,断面146的竖向位移由0 mm增加到0.3 mm,之后在顶管顶进过程中,竖向位移基本不变,断面116隆起量变化幅度较大,最大为0. 8 mm。在顶管施工过程中断面116的正向收敛最大,最大为0.6 mm,4月9日横向收敛减少,最大不超过0.3 mm,由实测数据看出最大的收敛值并不是发生在溢流井下方的断面146,而是发生在断面116,可能与左线隧道断面的突变有关,整体来看右线隧道的横向收敛小于左线。

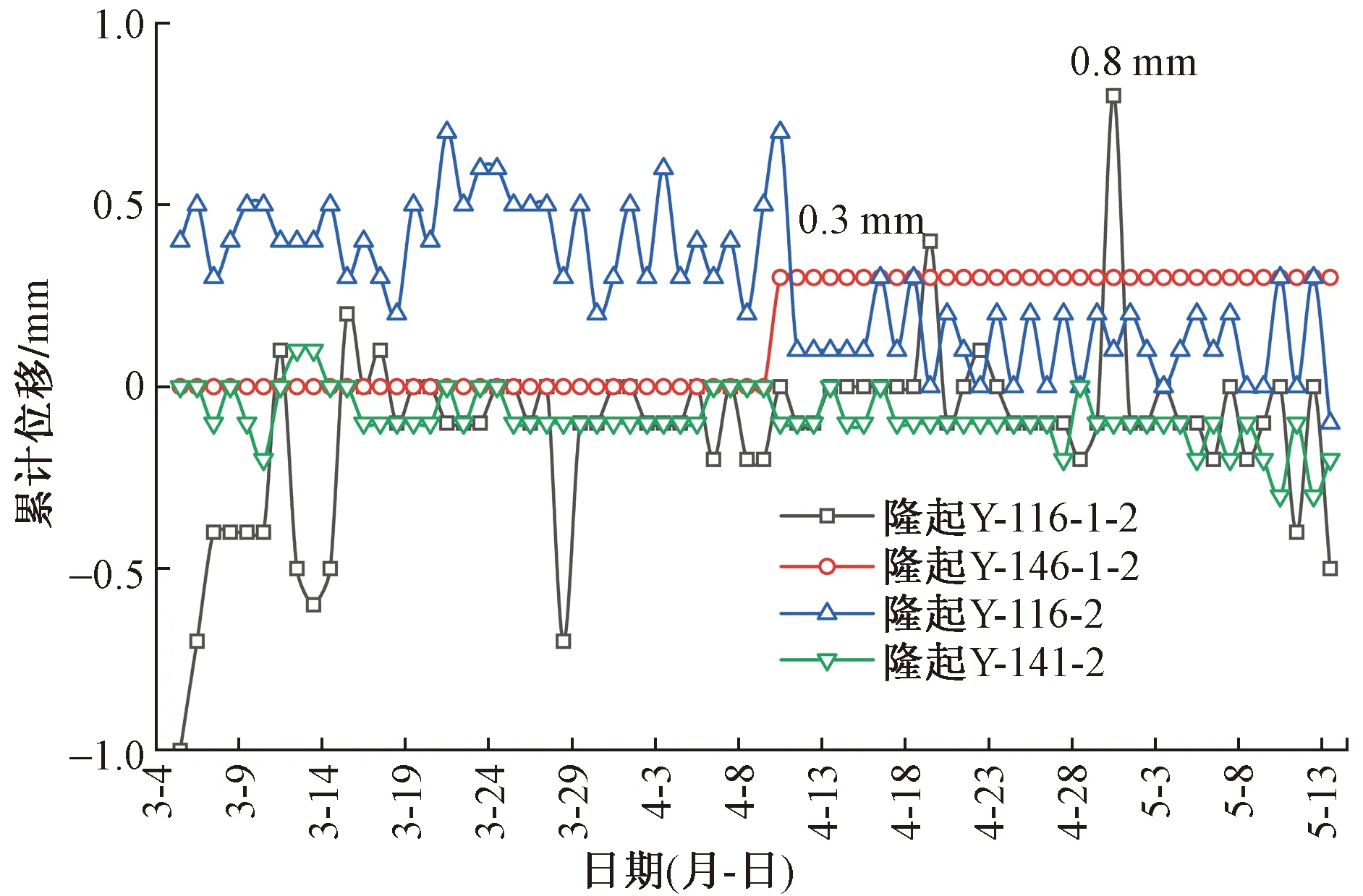
图10 右线隧道测点累计位移变化Fig.10 Cumulative displacement of monitoring points for right line

结合目前隧道现状已发生的沉降值和规范规定,在雨水管实施期间的地铁隧道位移指标控制值定为10.0 mm,隧道的累计位移值没有超过10.0 mm。

数值模拟结果对于最大隆起量的模拟与现场实测结果较为接近,对于横向收敛的模拟结果和现场实测数据有一定的出入,产生误差的原因主要如下。

(1)建立有限元模型时未考虑右隧道断面的突变。

(2)有限元模拟过程中采用在掌子面施加压力的方式模拟土体开挖,没有考虑管壁与土体的摩擦。

(3)有限元材料参数及土体模型产生的误差。

2.5 两种施工方式对比分析

由表2可以看出,顶管法施工左右线隧道的隆起量远小于明挖法,这可能是由于明挖法开挖面积较大,土体卸荷比较大,致使下卧地铁隧道发生较大上抬变形。但顶管法横向收敛大于明挖法施工,实际工程中应注意地铁隧道结构收敛变形的影响。

表2 两种施工方式对比表

3 下卧地铁隧道隆起量影响因素正交分析

3.1 正交试验设计

目前研究集中于单独研究基坑开挖或者顶管开挖对下卧隧道的影响,而在该工程中,由于溢流井在左隧道上方,雨水管道在右隧道上方,顶管法顶推及卸荷作用和基坑开挖卸荷作用均会影响下卧隧道的隆起量,且对隧道左右线的影响程度也不同,为研究顶管施工与基坑开挖两者共同作用下对下卧隧道的影响,采用正交试验法分析影响因子的敏感性,试验中仅考虑单条顶管顶进过程。

正交试验借助“正交表”可以以较小的实验次数分析各因素的重要性以及各因素对试验的影响,实验综合基坑开挖和顶管掘进共选取了基坑开挖深度、隧道埋深、顶管埋深、顶管半径和顶推力共5个因素(表3),每个因素下各有3个水平值,由于基坑开挖深度、隧道埋深、顶管埋深和顶管半径与卸荷引起的作用在隧道上的附加力有关,因此考虑这4种因素之间的相互作用,采用L27(313)正交表,共需进行27次实验。实验选择左右线隧道的最大竖向位移为考核指标,采用方差分析法与极差分析法分析正交试验的结果。

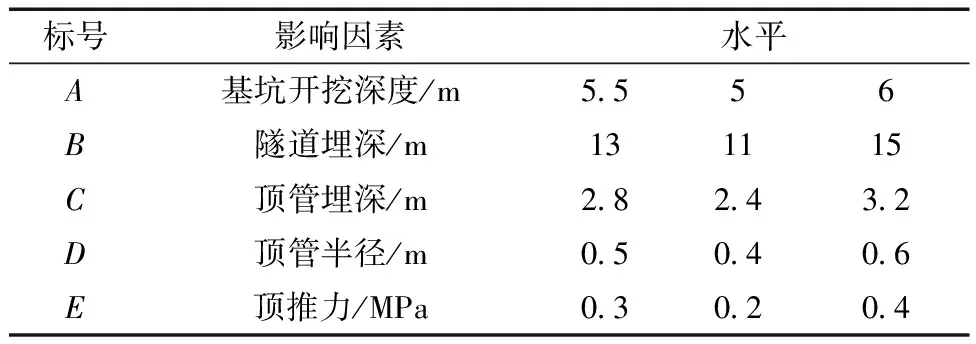
表3 正交试验因素水平表

3.2 左隧道正交试验结果分析

图11为各因素和左隧道最大隆起量(因素在每个水平下所有试验的平均值)之间的关系,左隧道的最大隆起量与顶管半径和基坑开挖深度成正比,与隧道埋深成反比,通过极差分析可知各因素对最大隆起量影响排序为:隧道埋深>基坑开挖深度>顶管半径>顶管力>顶管埋深。

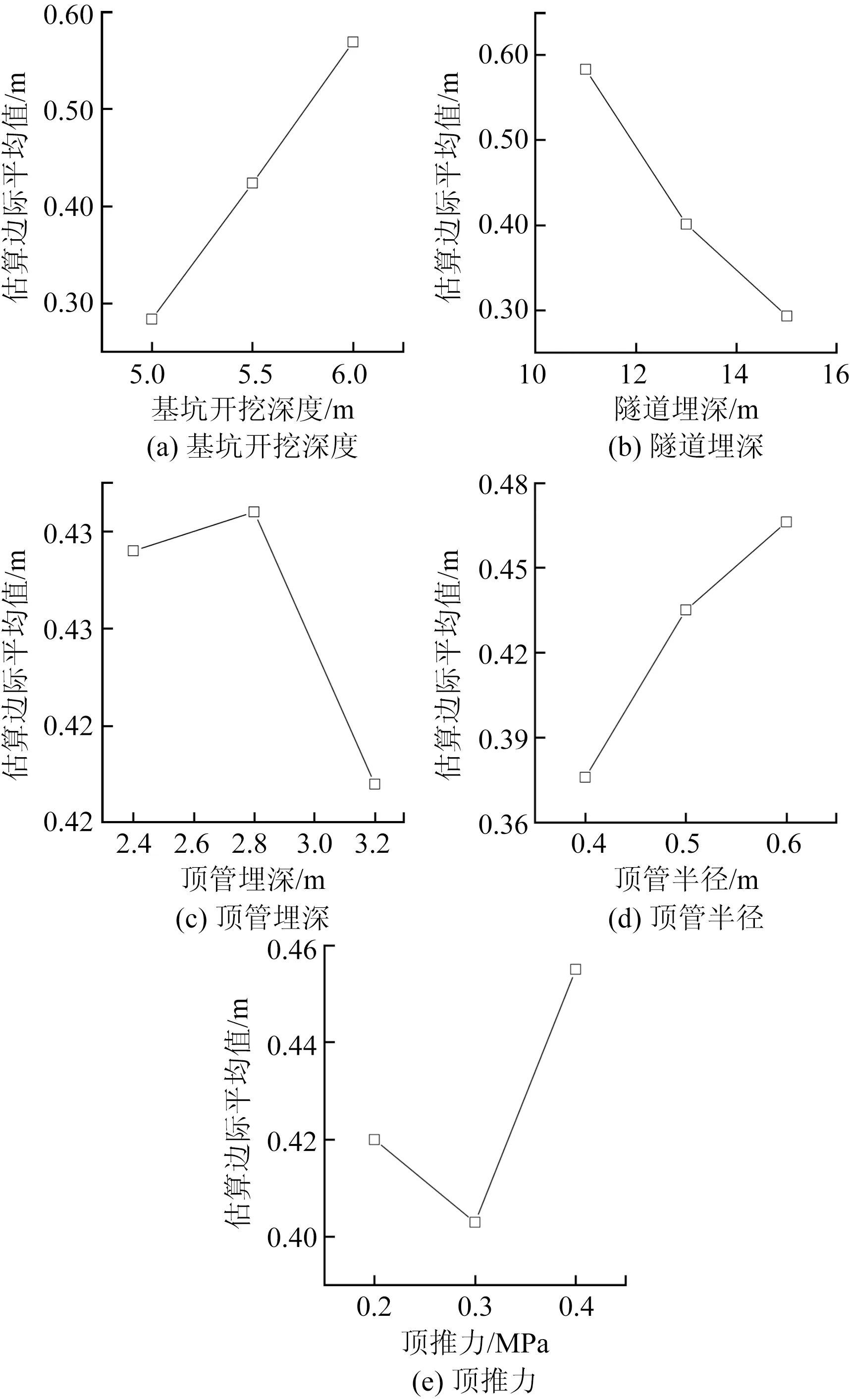
图11 左隧道最大隆起量和各因素关系Fig.11 The uplift of left tunnel varies with various factors

表4为左隧道最大隆起量与各因素之间的方差分析结果,由分析结果可以看出5个因素对左隧道的隆起量均有显著影响,影响程度排序和极差分析结果一致。则AB、CD、AC之间的共同作用对左隧道的隆起影响显著,影响程度排序为CD>AB>AC,AD、BD、BC共同作用对左隧道隆起无显著影响。

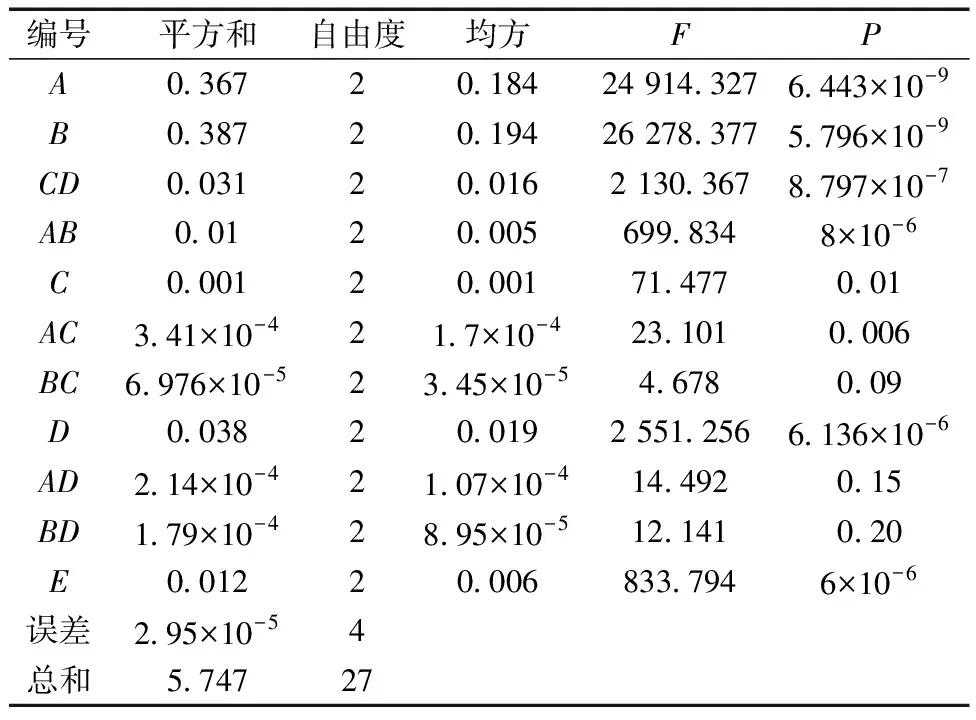
表4 左隧道方差分析法正交试验结果表

结合极差分析和方差分析结果,可以看出,由于左隧道处于基坑下方,所以与基坑开挖的相关因素隧道埋深、基坑开挖深度以及两者之间的共同作用对左隧道的隆起量影响较大,基坑开挖深度越大,隧道埋深越小,卸荷比越大,隧道的隆起量越大。管道处于右隧道正上方,与顶管法相关的因素对左隧道的影响相对较小。

3.3 右隧道正交试验结果分析

图12为各个因素和右隧道最大隆起量(因素在每个水平下所有试验的平均值)之间的关系,右隧道的最大隆起量与基坑开挖深度、顶管半径成正比,与隧道埋深成反比。通过极差分析可知各因素对右隧道最大隆起量影响排序为:顶管半径>基坑开挖深度>顶推力>隧道埋深>顶管埋深。

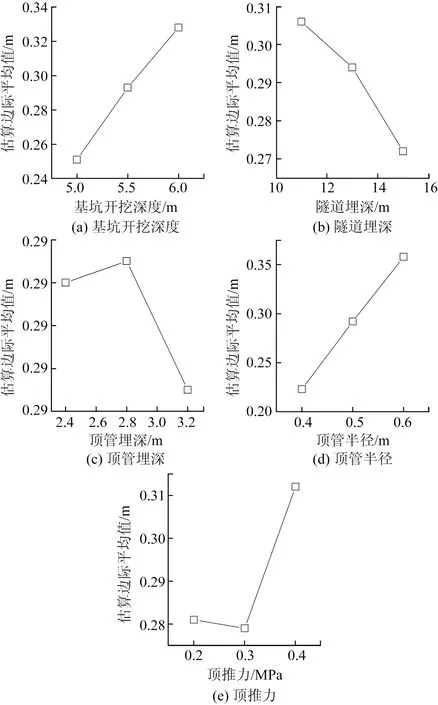
图12 右隧道最大隆起量和各因素关系Fig.12 The uplift of left tunnel varies with various factors

由表5可以看出,顶管半径、基坑开挖深度、顶推力和隧道埋深对右隧道隆起影响显著,顶管埋深为次要影响因素,与方差分析结果一致。CD、BD、AC之间共同作用影响显著,且CD>BD>AC。

表5 右隧道方差分析法正交试验结果表

结合极差分析与方差分析结果,由于雨水管道处于右隧道上方,与顶管法相关的因素顶管半径、顶推力、顶管半径和顶管埋深共同作用对右隧道的隆起量影响相对较大,顶管半径越大,顶管埋深越大,顶管施工的卸荷作用和顶推作用对下卧隧道产生的附加力越大,隧道隆起量越大。

从上述分析可知,左隧道的隆起量主要受基坑开挖的卸荷作用影响,右隧道的隆起量主要受顶管施工的顶推作用和开挖卸荷作用影响,对左隧道影响较大的因素为隧道埋深和基坑开挖深度,实际工程中可以通过控制基坑开挖的速度来控制下卧隧道的隆起速率,通过配重等方法抑制下卧隧道的隆起;对右隧道影响较大的因素为顶管半径与顶推力,实际工程中应注意控制顶推力同时不要超挖来减小对下卧隧道的影响。同时应该注意各因素之间不一定是相互独立的,需要考虑因素组合对下卧隧道隆起量的影响,上述分析中无论对于左隧道还是右隧道,顶管埋深和顶管半径的共同作用对下卧隧道的隆起量均有显著影响,因此在设计中需结合实际情况合理确定两者的取值。

4 结论

依托西安市雨水管道工程,采用数值模拟和实测数据分析两种方法,对比分析基坑开挖和顶管开挖下卧隧道变形规律,设计正交试验对下卧隧道隆起量影响因素的敏感性及交互作用分析,可得以下结论。

(1)采用明挖法施工时,下卧地铁隧道沿纵向5倍基坑开挖宽度内结构隆起量较大。渗流井基坑与管道基坑相继开挖对下卧地铁隧道的变形存在一定的叠加效应。基坑开挖后结构不均匀变形将使左隧道断面会发生扭转,右隧道断面发生竖向拉伸。

(2)采用顶管法施工可以减少下卧隧道结构的上抬变形,随着顶管推进,下卧隧道隆起量逐渐增大,上穿下卧隧道时隆起量增加最快,之后隆起量基本保持不变。实测数据表明顶管法会使下卧隧道产生较大的横向收敛,最大为1.7 mm,实际工程中应注意控制地铁结构收敛变形。

(3)基坑开挖和顶管施工共同作用时,各因素对左右隧道的影响程度不同,左隧道的隆起量主要受基坑开挖卸荷作用影响,右隧道的隆起量主要受顶管施工的顶推作用和开挖卸荷作用影响。同时应注意各因素之间不一定是相互独立的,需要考虑因素组合对下卧隧道隆起量的影响。