光纤拉曼放大器在单芯反馈式结构中的偏振相关性研究

沈礼谋,贾 波,肖 倩

(复旦大学 材料科学系,上海 200433)

随着光纤通信技术中波分复用(Wavelength-Division Multiplexing,WDM)技术的不断进步,光纤放大器在长距离传输中的作用越来越受到重视。早期,掺铒光纤放大器(Erbium-Doped optical Fiber Amplifier,EDFA)得益于其高能量利用率和显著的增益效果而被广泛关注。而随着通信带宽的增加,EDFA 增益波段的固定导致其在通信系统中的应用局限性越来越明显。因此,可实现任意波段放大的光纤拉曼放大器(Fiber Raman Amplifier,FRA)成为了新的研究热点。

FRA 是基于受激拉曼散射(Stimulated Raman Scattering,SRS)制成的分布式光纤放大器。SRS的原理是频率为ωp的入射光与材料分子光学支声子进行能量交换,受激辐射产生低频的斯托克斯光ωs。频率差Δω=ωp-ωs称为拉曼位移,它与物质分子的特性有关。石英光纤的Δω为13.2THz,当入射泵浦光波长为1455nm 时,波长在1555nm 附近的光将产生SRS,由此可以放大该波段的工作光。在石英光纤中,FRA 放大的波段仅与泵浦光的波长有关,理论上可以放大任意波段,并且不同波长的泵浦源制成的多级FRA 可以实现远超EDFA 的增益带宽[1-3]。

由于FRA 的拉曼增益对偏振十分敏感,而被称之为FRA 的偏振相关增益(Polarization Dependent Gain,PDG)。Tobin等[4]、Mahgerefteh等[5]和张敏明等[6]发现了在拉曼谐振腔中垂直偏振时的增益系数是平行偏振时的增益系数的十分之一。Daniel等[5]在低偏振模色散(Polarization Mode Dispersion,PMD)的光纤中观察到了FRA 显出明显的PDG。再后来,众多研究指出PMD 会导致光纤中工作光在传输过程中偏振态改变。在足够长距离的传输后,PMD 会降低工作光的偏振度(Degree of Polarization,DOP),使得FRA 的PDG 减弱,偏振敏感性降低。并且,FRA 同向泵浦结构的PDG 显著强于相向泵浦[7]。为降低PDG 的影响,通常会对FRA 的泵浦光源直接进行退偏振处理,常见的退偏方式为正交泵浦源偏振合光法和光谱平均法[8]。

而制作完全退偏的拉曼泵浦光源难度很高,市面上的退偏拉曼泵浦光源的质量参差不齐。因此本文引入单芯反馈式结构,围绕FRA 增益的偏振相关性和FRA 增益对偏振态的影响进行了机理分析和实验验证。研究在该结构中,FRA 放大前后的偏振态变化和从光路层面上降低FRA 的PDG 影响的方法。

1 理论方法

1.1 拉曼放大器传输理论

考虑瑞利散射(Rayleigh Scattering,RS)和放大自发辐射(Amplifier Spontaneous Emission,ASE),同时包含同向和相向泵浦的被FRA 放大的工作光的传输方程[2,9-10]可表示为

其中: +和-表示光传输方向;α表示在光纤中的传输损耗;γ为瑞利散射系数;gr(ν-ζ)表示频率ν和ζ之间的拉曼增益系数;Keff为泵浦和工作光之间的偏振相关系数;Aeff为有效模式面积;h为普朗克常数;k为玻尔兹曼常数;T是光纤绝对温度。

针对固定的泵浦和工作光波长,拉曼增益系数gr是定值,通常认为是将能够得到最大拉曼增益的工作偏振态的拉曼增益系数,该偏振态称为优势偏振态。设优势偏振态增益系数为g‖,与其正交的偏振态增益系数为g⊥,两个偏振方向的工作光的光功率分别设为P‖和P⊥,则总的拉曼增益系数gt可表示为

偏振相关系数Keff与FRA 的PDG 有关,本文建立了Keff与拉曼增益系数之间的关系,表示为

当输入的工作光处于优势偏振态,即P⊥=0时,此时Keff的值为1;当输入的工作光处于正交偏振态,即P‖=0时,Keff的值为g‖/g⊥,因g‖≫g⊥,则Keff取∞;当输入的工作光偏振态处于扰偏状态,即P‖=P⊥时,优势偏振态和其正交偏振态都不占优势,Keff的值为2g‖/(g‖+g⊥),因g‖≫g⊥,则Keff取2,以上Keff的取值与过去的研究相符合。

有效模式面积Aeff与光纤有效纤芯半径ωeff有关,可表示为

根据AOKI Y[11]提出的理论模型,拉曼增益Gr可表示为与泵浦光功率Pp和拉曼增益系数gr相关的形式,其式为

其中:Leff为拉曼增益的有效长度,它与泵浦光传输损耗系数αp和泵浦光传输距离z有关,表达式为

从式(5)、式(6)中可发现,拉曼增益Gr与拉曼泵浦功率、泵浦偏振态及泵浦传输距离(增益光纤长度)有关。Gr随泵浦功率增大而增大,随增益光纤长度增大而增大,随偏振相关系数Keff取值增大而减小。

1.2 偏振态变化度量

设沿光纤截面建立的x、y轴上光的振动分量的电矢量分别为Ex和Ey,则定义斯托克斯(Stokes)参量如下所示:

其中:δ=δy-δx,表示Ey和Ex的相位差;S0表示偏振光的光强;正的S1表示x轴方向直线偏振光分量,负的S1表示y轴方向直线偏振光分量;正的S2表示45°方向直线偏振光分量,负的S2表示-45°直线偏振光分量;正的S3表示右旋圆偏振光分量,负的S3表示左旋圆偏振光分量。完全偏振光满足

部分偏振光满足式

偏振度P为光强中完全偏振光的比例,可表示为

偏振度只能衡量完全偏振光的比例,无法准确描述待测光偏振态。比较斯托克斯(Stokes)参量变化又不够直观,因此引入庞加莱(Poincare)球。用斯托克斯(Stokes)参量建立的庞加莱球如图1所示。

图1 庞加莱球示意图Fig.1 Schematic diagram ofPoincare ball

当只对偏振态感兴趣时,通常对S0归一化处理,即去除部分偏振光中的非偏振光部分。任意光的偏振态对应特定的斯托克斯参量,都可用庞加莱球面或内的一个点坐标表示,此时斯托克斯参量满足

其中:β表示椭圆偏振光的椭圆率角,指椭圆短轴分量和长轴分量之比的反正切值,即

θ表示椭圆偏振光的长轴方位角,即椭圆长轴与光纤x轴所成夹角,数值上等于在y轴和x轴上分量的比值,即[12-14]

β和θ示意图如图2所示。

图2 椭圆偏振光的椭圆率角β 及长轴方位角θ 示意图Fig.2 Schematic diagram of ellipticity angleβ and long axis azimuthθ of elliptically polarized light

由式(10)、式(11),解得椭圆角率β和椭圆长轴方位角θ的表达式为

设偏振态变化前后的椭圆率角分别为β0和β,方位角分别为θ0和θ。用它们的差值Δβ和Δθ分别表示椭圆偏振光的椭圆形状变化程度和椭圆旋转角度,用以评判偏振态的变化情况,即

1.3 偏振相关增益波动系数

FRA的偏振相关性指FRA增益随工作光与泵浦光偏振角度不同而改变的特性,称为FRA 的偏振相关增益PDG[15-17]。FRA的增益Gr通常指拉曼开关增益Gon-off,即开启FRA 工作光的输出功率Prs和关闭FRA工作光的输出功率Ps的比值,为便于计算,使用对数表示拉曼开关增益(单位为dB),其式如下所示:

由式(5)可知,Gon-off(即Gr)与FRA 的偏振相关系数Keff有关,体现为PDG。当工作光输入偏振态变化时,因PDG 引起拉曼增益也会发生波动,波动程度可以用Gr的标准差σ(Gr)表示。定义Gr的标准差系数为FRA 的偏振相关增益波动系数ωPDG,即

ωPDG可衡量FRA增益引起的PDG,ωPDG的值越大,Gr的波动越大,PDG 越明显。

1.4 单向泵浦结构输出光偏振态分析

对于单向泵浦结构,即工作光和泵浦光在光纤中仅单向传输。设光纤中z处的椭圆偏振光如图3所示,此时,FRA 的优势偏振态恰与光纤慢轴y轴重合,为便于分析,设优势偏振态为线偏振。

图3 光纤中z 处椭圆偏振光Fig.3 Elliptically polarized light at z in the fiber

椭圆偏振光在x轴和y轴上的电矢量波动程可写为

将式(18)写为复振幅形式,其中(ωt-kz)为定值可忽略,则复振幅可写为

此时,δ=δy-δx为相位差,它们的振幅比角α满足

振幅比角α、相位差δ、椭圆率角β及椭圆长轴方位角θ之间的关系满足

由式(20)、式(21)可得到β和θ的表达式如下

当FRA 开启后,两个偏振态的振幅满足

若相位差δ不变,则此时拉曼增益后的工作光椭圆率角βr和长轴方位角θr分别为

比较式(22)和式(24),发现开启FRA 后,工作光的椭圆率角和长轴方位角都发生了变化,即拉曼增益会影响工作光的偏振态。

1.5 单芯反馈式结构输出光偏振态分析

单芯反馈式结构,即工作光输入光纤并传输一段距离后,在光纤尾端经法拉第旋转镜(Faraday Rotating Mirror,FRM)反射回到光纤中反向传输,最后在输入端处输出,其基本结构如图4(a)所示。

图4 单芯反馈式结构偏振态变化Fig.4 Polarization state changes of single-core feedback structure黄色圈里的A、B、C表示光纤上的某一位置

设光纤上紧邻FRM 的一点为A,从A 处进入FRM 的工作光为pass光,从FRM 返射到光纤中的光设为reflect光,pass光功率可以分解为正交的P‖pass和P⊥pass,reflect光功率可以分解为P‖reflect和P⊥reflect,‖和⊥分别表示拉曼优势偏振态和正交偏振态。

当FRA 关闭时,如图4(a)所示。由于FRM 的特性,A 点处的reflect光的偏振态是pass光偏振态旋转π/2后的结果,若忽略FRM 损耗,则pass光和reflect光分量功率满足

当FRA 开启时,如图4(b)所示。此时,由于FRA 具有的偏振增益特性,且优势偏振态光分量受到g‖的拉曼增益,正交偏振态光分量受到g⊥的拉曼增益,则A 处pass光分量满足

工作光被FRM 反射后,到达A 处的reflect光分量由于偏振旋转,其光分量满足

分量的比值满足

从式(28)可发现,无论FRA是否开启,经FRM 反射后到达A 处的reflect光的两个偏振分量的光功率比值相同,此时光的偏振态不会发生改变。鉴于以上分析,对于紧邻A 点的B点,反向输出光的偏振态亦为正向输入到B点的光的偏振态旋转π/2后的结果,等同于FRM 直接接在B点之后;对于紧邻B点的C点亦是如此。以此类推,从光纤输入端反向输出的工作光的偏振态也为此处正向输入光偏振态旋转π/2的结果。并且,单芯反馈式结构中来回传输的工作光两个偏振角度受到的拉曼增益是相同的,reflect光的合光功率满足

可发现,reflect光的光功率仅与无FRA 增益的pass光的光功率有关,而g⊥·g‖为常数,因此,若增益光纤长度不变,pass光的光功率不变,总是不变的,即输出端工作光获得的总的拉曼增益是稳定的,不受输入端输入光的偏振态的影响。

综合以上推论,可认为FRA 的增益特性并不会影响单芯反馈式结构中工作光自身的输出偏振态,工作光在该结构的光纤中传输后,输出光能获得稳定的拉曼增益。

2 实验与讨论

单向泵浦可分为同向泵浦和相向泵浦两种结构,分别为工作光与泵浦光同向和相向传输,光路分别如图5(a)和(b)所示;单芯反馈式结构的光路如图5(c)所示,实验装置如图6所示。

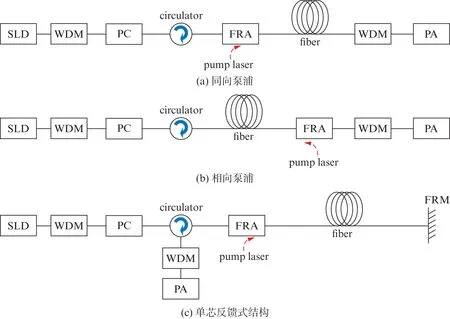
图5 光路结构图Fig.5 Diagram of the optical path structure

图6 实验装置Fig.6 Experimental device

图5(a)和(b)引入环形器(circulator)是为了与单芯反馈式结构形成对照,不影响单向泵浦结构的测试结果。超辐射发光二极管(Superluminescent Light-emitting Diode,SLD)用作发出工作光的光源;WDM 是波分复用;FRA 的泵浦为偏振光(未退偏泵浦);偏振控制器(Polarization Controller,PC)可以改变工作光的输入偏振态,包括固定偏振态(stable)和扰偏状态(scramble);偏振分析仪(Polarization Analyzer,PA),可检测工作光的输出偏振态,包含斯托克斯参量及庞加莱球信息,同时可检测光功率。

设当PC处输入偏振态不变时,关闭和开启FRA,输出端工作光的椭圆率角为βr和β0,方位角为θr和θ0,它们的差值Δβr和Δθr满足式

实验用FRA 的泵浦电流为250mA,增益光纤为50km 时,输出端工作光的庞加莱球如图7所示,其中红点对应PA 处检测到的输出偏振态。从图7可发现,开关FRA,单芯反馈式结构的输出偏振态对应的红点位置变化小于同向和相向泵浦结构。根据式(14)、(15)和(30),开关FRA,同向泵浦、相向泵浦和单芯反馈式结构的偏振变化量如表1所示。

表1 3种结构开关FRA时,Δβr 和Δθr 值Tab.1 Values of Δβr and Δθr when switching FRA of three structures

图7 增益光纤50km 时,输出端工作光偏振态Fig.7 When the gain fiber is 50km,the polarization state of the working light at the output end

从表1中可发现,在50km 的增益光纤长度下,单芯反馈式结构的Δβr和Δθr小于单向泵浦,即输出端工作光偏振变化量更小。

为观察偏振变化与长度的关系,测试在不同增益光纤长度时,3种光路结构开关FRA,输出光Δβr与Δθr随增益光纤长度LGF的变化情况,实验结果分别如图8(a)、图8(b)所示。

图8 开关FRA,偏振态变化量随增益光纤长度变化Fig.8 When the FRA is switched on and off,the change of polarization state varies with the length of the gain fiber

由图8发现,单芯反馈式结构的偏振态变化量小于同向泵浦和相向泵浦,表明开关FRA,单芯反馈式结构的输出端工作光偏振态几乎不变,证实了理论分析中的推论,即拉曼增益不影响工作光的输出偏振态。而同向泵浦和相向泵浦时,PMD 造成的椭圆偏振光偏振态的随机改变以及拉曼增益的偏振相关性,使得其椭圆率变化量和椭圆方位角变化量数值变化具有随机性,因此在数值上存在不规则波动,对实验结论没有影响。

基于上述不同增益光纤长度的实验,测试开关FRA 时输出端PA 处的输出光功率,据式(16)、(17)计算泵浦的FRA 开关增益Gon-off和其偏振相关增益波动系数ωPDG,得到3 种光路结构的ωPDG随增益光纤长度变化的结果如图9所示。

图9 偏振相关增益波动系数ωPDG 随增益光纤长度变化Fig.9 Polarization dependent gain fluctuation coefficient ωPDG varies with the length of the gain fiber

由图9可发现,单向泵浦中,同向泵浦的ωPDG大于相向泵浦的ωPDG,表明PDG 在同向泵浦中表现明显,这与过去的研究结果相符合。随着光纤长度继续增大,单向泵浦的ωPDG不断减小,其原因为不理想的单模光纤PMD 使得光纤长距离传输后的工作光的偏振态不断改变,最终在长距离传输后偏振态逐渐平均。此时,FRA 带来的PDG 影响下降,表现为ωPDG降低。

同时,观察到单芯反馈式结构的ωPDG在不同增益光纤长度下都小于单向泵浦,即单芯反馈式结构的拉曼增益受偏振影响小于单向泵浦结构,PDG 更小,能获得更稳定的拉曼增益,印证了理论部分的推论。

3 结语

FRA 的增益对偏振敏感,PDG 使得偏振的工作光无法获得稳定的增益。过去常用对FRA 泵浦退偏的方式来降低PDG 的影响,这对退偏泵浦的设计、工艺等有较高的要求,从而很难获得理想退偏的泵浦。

为了在光路层面上降低PDG,本文引入椭圆率角变化量Δβ、椭圆长轴方位角变化量Δθ和偏振相关增益波动系数ωPDG,用以衡量偏振态变化量和FRA 拉曼增益受PDG 的影响。本文从机理上揭示了在单芯反馈式结构中应用FRA 受PDG 影响较小的原因,然后采用泵浦未退偏的FRA 设计了测试输出偏振态以及PDG 的实验。实验结果表明: 在该泵浦条件下,应用FRA 的单芯反馈式结构输出光的偏振变化量小于单向泵浦,表明其输出光偏振态几乎不受FRA 增益影响;并且,单芯反馈式结构的偏振相关增益波动系数同样低于单向泵浦,即拉曼增益受偏振影响更小,单芯反馈式结构中应用FRA 能获得比单向泵浦更稳定的拉曼增益。以上实验结果验证了理论研究部分单芯反馈式结构输出光偏振态几乎不变且工作光受到的拉曼增益几乎不受PDG 影响的推论。因此,将FRA 应用在单芯反馈式结构中可以一定程度上减弱其偏振敏感性。