新型模型参考自适应的PMSM无差拍电流预测控制
张懿, 徐斌, 魏海峰, 李垣江, 刘维亭
(江苏科技大学 电子信息学院,江苏 镇江 212100)
0 引 言
永磁同步电机(permanent magnet synchronous motor,PMSM)具有体积小、质量轻、功率高等特点,因此广泛普及于民用、航天及军事等领域。当前,电流环控制策略有:电流预测控制[1-4]、电流滞环控制[5-8]、PI电流控制[9-12]和自抗扰控制[13-14]等。截至目前,应用最广的是传统PI电流环控制,由于其结构简单以及低通滤波的特性,导致超调量较大,适用于滞后性和惯性比较大的场合。电流滞环控制的算法比较复杂,并且其开关频率受负载的影响较大,而自抗扰控制研究目前还未达到一定的深度,因此算法实现难度大。为了满足高精度领域的需求,无差拍电流预测控制可以让系统的电流环得到更快的响应输出,同时电流的纹波小,控制算法也容易实现,但由于无差拍电流预测控制受电机参数的影响较大,当电机参数不准确或者工作环境改变,都会导致交直轴电流出现偏差,随着转速的增大,交直轴电流偏差就会越大。文献[15]设计了基于Lagrange插值的无差拍电流预测控制 (deadbeat predictive current control,DPCC)算法,虽然提高了鲁棒性,但也降低了一定的动态效果。文献[16]提出了一种新的功率滑模趋近律,缩短系统的收敛时间,然后建立了一种改进功率滑模趋近律的非齐次扰动观测器,保证电流误差收敛至0,最后建立一种新型定子电流和扰动观测器的改进型DPCC。模型参数扰动的问题基本得到解决,但是计算复杂,对计算机硬件要求高。文献[17]在无差拍电流预测控制中引入鲁棒电流预测算法,提高了系统电流环的动态性能和稳态精度,但是研究对象只针对电感参数失配,在实际应用中,电机运行受限不只是电感参数的问题。文献[18]通过加入模糊前馈控制器来降低参数的敏感度,从而提高鲁棒性,但是目前只停留在仿真阶段,没有考虑实际应用环境中的电机控制,缺乏实验依据。文献[19]提出了一种非线性扩展状态观测器和权重因子相结合来改进DPCC的方法,估计的电流扰动和电压扰动可以分别用来校正电流参考值和输出电压,以此提高系统的鲁棒性,但设计过程较为复杂。文献[20]为了实现让电流误差为0,需要提供补偿给反馈电流,将引入电流预测的补偿因子来修正电压,以此提高系统的鲁棒性,但是该方法比较影响系统的动态性能。
为了解决由于参数失配导致无差拍电流预测控制动态跟踪性和鲁棒性差的问题,本文提出一种基于新型模型参考自适应系统的参数分步辨识法。首先获取定子电感和定子电阻参数,将其作为已知量来辨识转子磁链。等到转子磁链参数稳定后,再针对定子电阻和定子电感进行辨识。其次,将辨识出的参数代入无差拍电流预测控制进行改进,可以有效解决参数辨识模型存在的欠秩问题,增加电机参数辨识的精确度,同时可以抑制参数失配对无差拍电流控制系统的影响,从而提高系统的动态跟踪性和鲁棒性。最后通过实验验证该方法的有效性。
1 无差拍电流预测控制
1.1 永磁同步电机数学模型搭建
为了简化设计,因此假设PMSM满足以下理想情况:
1)忽略电机的铁心饱和;
2)不计涡流和磁滞损耗;
3)电机电流为对称的三相正弦波。
基于以上理想情况,永磁同步电机在d-q轴下的定子电压方程为:
(1)
式中:ud、uq和id、iq分别是d-q轴下的定子电压和定子电流分量;Rs是定子电阻;Ld、Lq是d-q轴电感;ωe是转子电角速度;ψf是转子磁链。
1.2 无差拍电流预测控制的实现
采用表贴式永磁同步电机,利用其d-q轴电感相等的特性,即Ld=Lq=L。将d-q轴电流作为状态分量,得到的电流状态方程数学模型为:
(2)
由于电流的采样时间短,则本文采用一阶泰勒公式将电流状态方程进行离散化,即离散化的数学模型近似为:
(3)
式中:id(k)、iq(k)是第k时刻的d-q轴电流变量值;id(k+1)、iq(k+1)是第k+1时刻的d-q轴电流变量值;Ts是电流的采样时间值。通过将式(3)代入式(2),可以计算出无差拍电流预测控制中第k+1时刻的离散化d-q轴电流变量值控制方程为
(4)
式中:
无差拍电流预测控制的实际意义是为了实现控制系统下一刻的输出电流能够跟上给定电流,则需要将控制系统的给定电流值作为下一个时刻的输出电流值,因此,需要根据离散方程和d-q轴的给定电流值计算出控制电压,以此来实现下一时刻的输出电流经过单独的电流采样周期后能够跟上给定电流。通过式(4)可以计算出无差拍电流预测控制中所需的d-q轴电压控制方程为
(5)
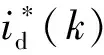
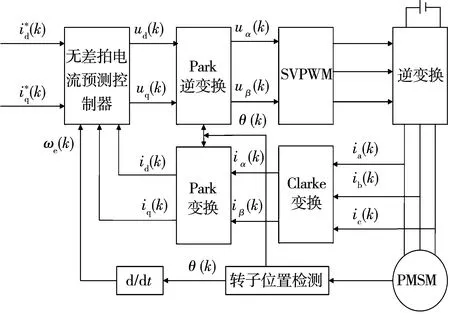
图1 无差拍电流预测控制系统结构框图Fig.1 Structural block diagram of traditional DPCC system
(6)
在实际进行永磁同步电机控制过程中,基于电机参数准确的情况下,则在第k+1时刻的d-q轴输出电流值将会达到给定电流值。若电机参数失配的情况下,则第k+1时刻的d-q轴输出电流值将会和给定电流值出现误差。根据式(4)可以计算出无差拍电流预测控制中第k+1时刻的离散化d-q轴实际电流变量值控制方程为
(7)
式中:
其中:Rs0是定子电阻实际值;L0是定子电感实际值;ψf0是转子磁链实际值。
将式(6)代入式(7)可得:
(8)
式中:ΔR=Rs-Rs0;ΔL=L-L0;Δψ=ψf-ψf0。
当系统达到稳定时刻,可从上式看出,定子电阻和定子电感均会影响d-q轴电流,而转子磁链只会影响q轴电流。由此可见,电机参数的精度偏差会影响整个电机电流环控制的性能,因此,增加电机参数辨识的精度就可以抑制参数失配对电机的性能影响,使得整个控制系统运行具有稳定性。
1.3 无差拍电流预测控制的稳定性
基于Ts的开关周期很小,因此将式(8)进行Z变换,可以得出d-q轴给定电流和实际电流的离散域闭环传递函数为
(9)
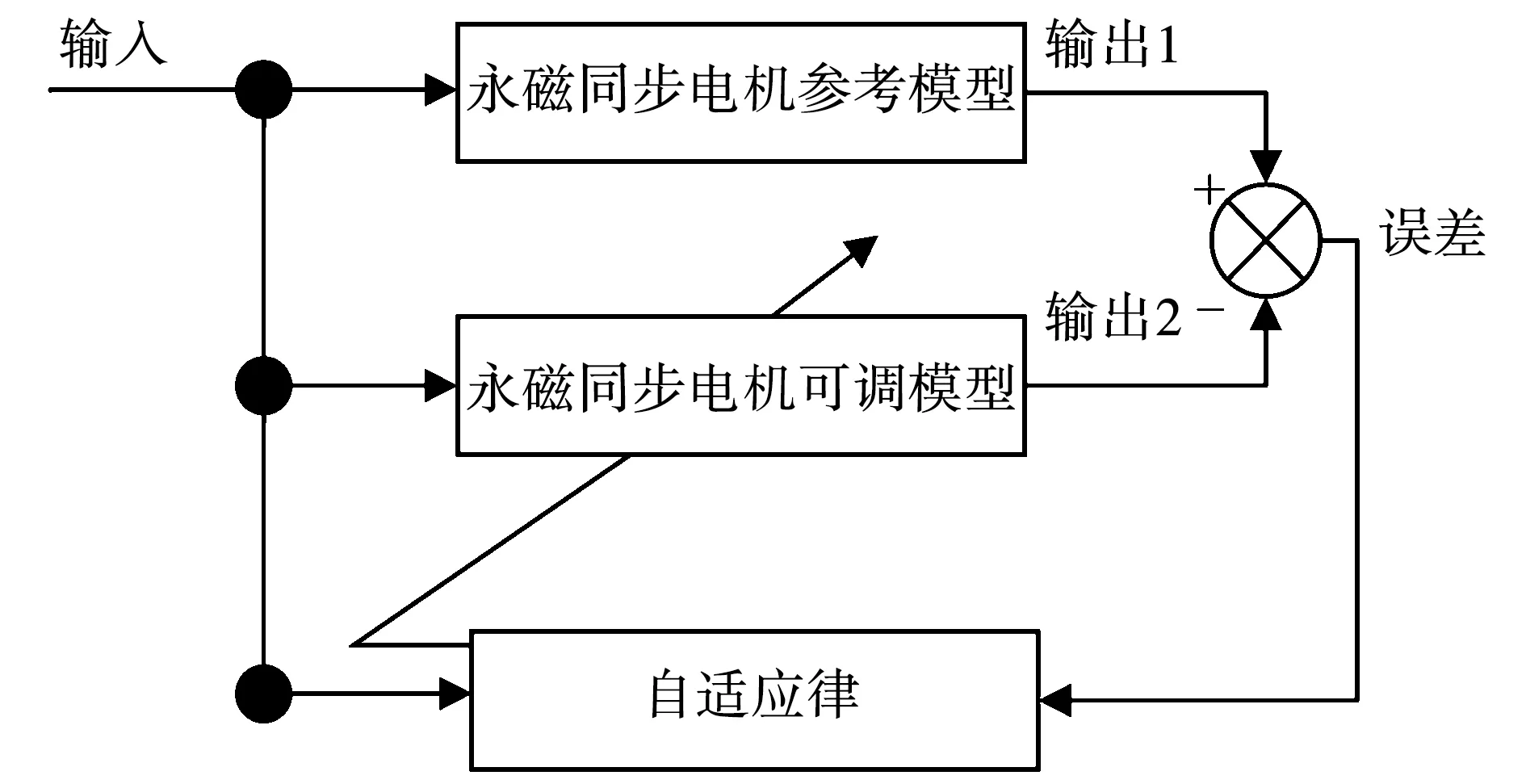
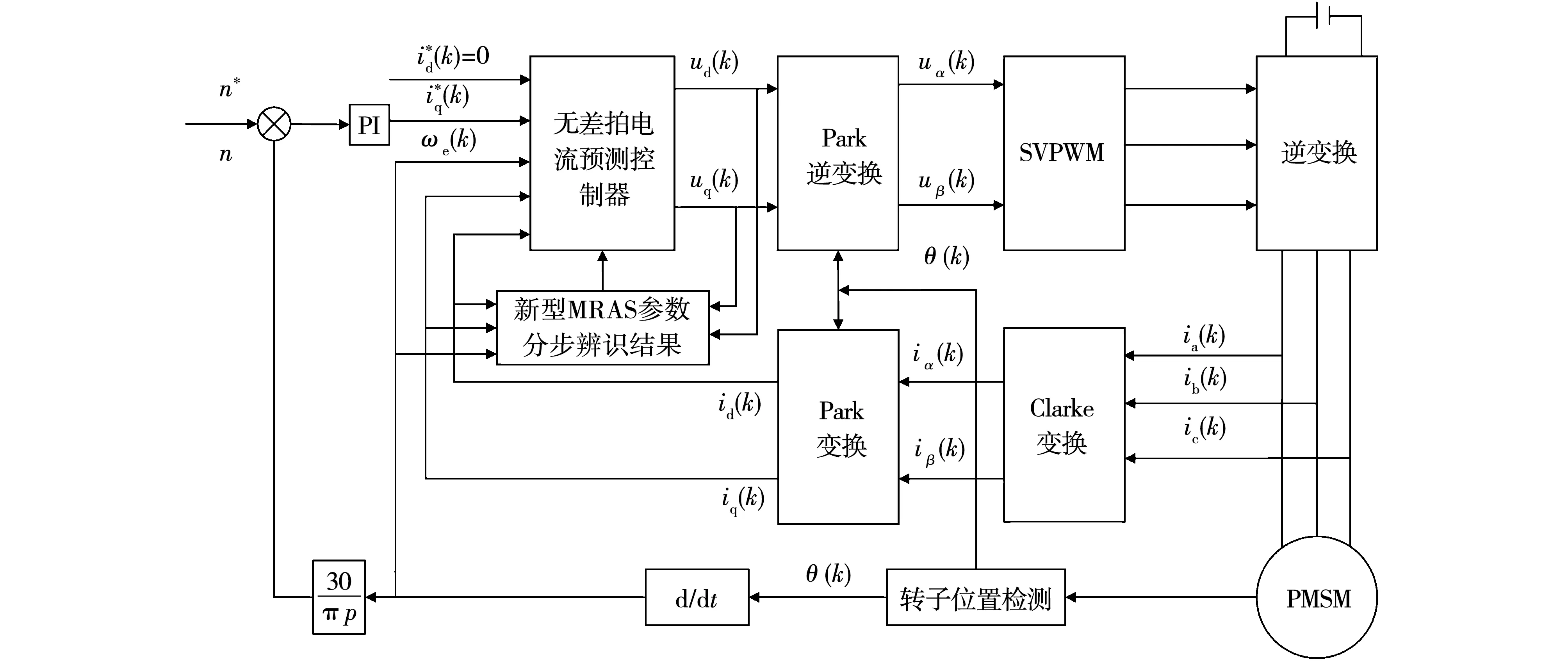
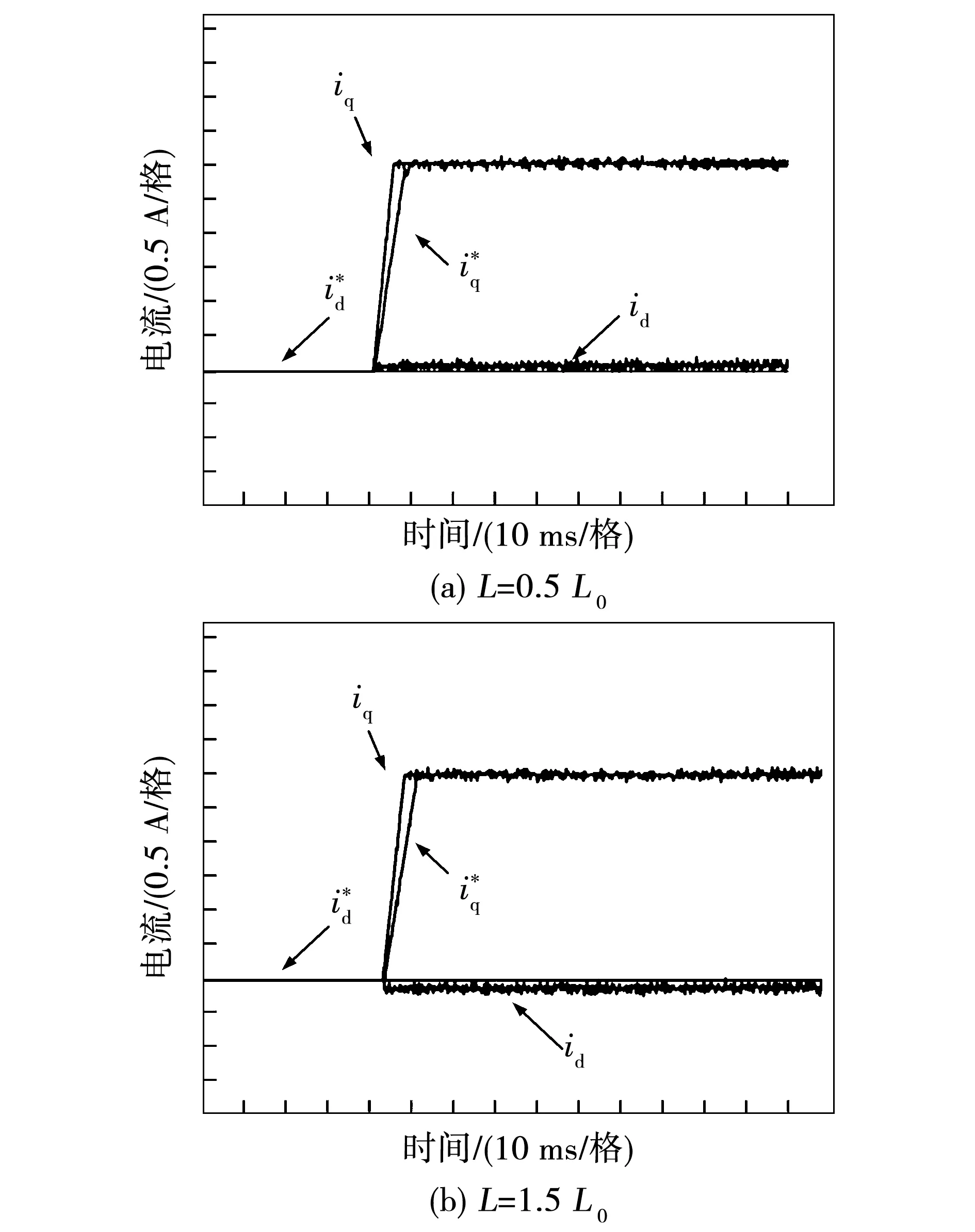
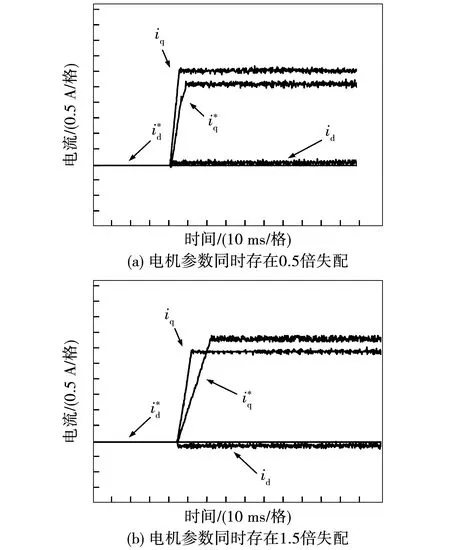
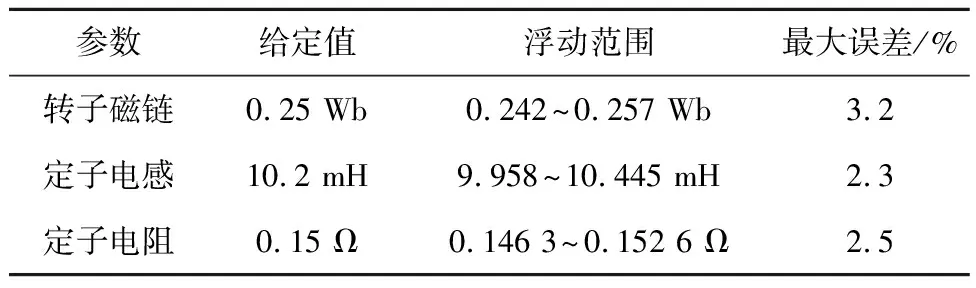
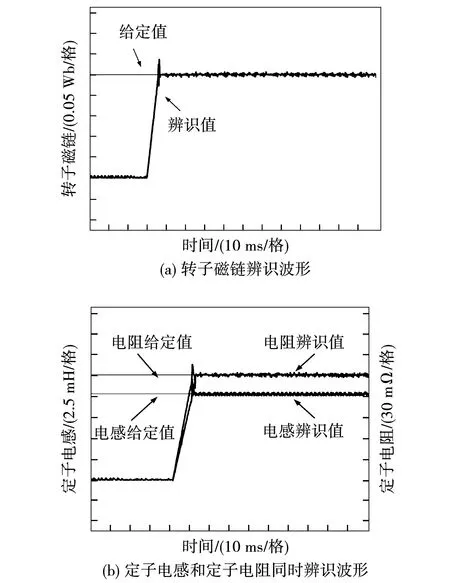
0 (10) 由式(10)可知,要使系统稳定,则定子电感值需在该范围内,假如超出该范围,则系统是不稳定的。 图2为传统模型参考自适应系统(model reference adaptive system,MRAS)结构框图,由参考模型、可调模型和自适应律共同组成。该系统主要实际意义在于求得一种能够实时进行动态调整的反馈自适应律,使得当前系统的闭环控制性能可以和参考模型的性能相一致,因此构造出两个模型,其中一个将不含待辨识参数的电流状态方程作为永磁同步电机参考模型,而将含待辨识参数的电流状态方程作为永磁同步电机可调模型,将这两个模型输出量作差,当得出的输出误差送入自适应律进行实时动态调整至0时,则可调模型就等效于参考模型,而待辨识参数的估算值就等效于参数的实际值。本文结合Popov超稳定性理论设计自适应律,该设计方法可以降低计算量,同时可以保证待辨识参数的稳定性。 图2 传统模型参考自适应系统结构框图Fig.2 Structural block diagram of traditional MRAS system 如式(2)所示,永磁同步电机数学模型的电流状态方程是2维的,在需要辨识电机3个参数的情况下,会存在欠秩情况,从而导致电机参数的失配,影响电机的控制性能。因此,本文采用参数分步辨识的方法,其系统结构框图如图3所示。 具体的辨识过程如下: 1)固定定子电阻和定子电感,以上电机参数均可从电机参数铭牌上获取; 2)将不含待辨识参数的电流状态方程作为永磁同步电机参考模型,将步骤1获取到的定子电阻和定子电感参数值作为已知量代入进电流状态方程中,设计出含待辨识参数的可调模型。由于转子磁链只和q轴电流状态方程相关,所以只需采用q轴电流状态方程即可。此时只有一个未知量,方程存在唯一解,从而设计自适应律来辨识转子磁链; 3)待转子磁链辨识稳定后,将已知的转子磁链代入第二个可调模型中,用来辨识定子电阻和定子电感,此时只有2个未知量,针对2维的电流状态方程存在唯一解,再设计自适应律来辨识定子电阻和定子电感。 由于转子磁链只和q轴的电流方程有关,通过式(2)可得q轴的电流状态方程为 (11) 对应的可调模型为 (12) 由式(11)~式(12)可得一阶误差系统为 (13) 为了满足该系统的全局稳定,根据Popov超稳定性理论可知,需要满足以下条件: (14) 式中γ2是有限正数。将eq和F代入式(14)可得: (15) 这里将转子磁链的自适应律设置为比例积分形式,具体形式如下: (16) (17) 将式(17)拆分成积分项和比例项,即: (18) (19) 将式(19)代入式(18)可得: (20) 式中ki和kp均大于0。由式(20)进行变换可得: (21) 由式(21)可知,式(18)成立,因此式(17)成立。即该系统全局稳定,则有: (22) 因此,将式(22)代入式(16)并化简,转子磁链的自适应律为 (23) 当转子磁链辨识稳定后,对定子电阻和定子电感进行辨识,通过式(2)可得参考模型为 (24) pI=AI+BU+C。 (25) 可调模型为 (26) 电流状态方程式(26)可化简为 (27) 将式(25)减去式(27)得 (28) pe=Ae-F。 (29) 根据上述的Popov稳定性定理,要想使反馈系统保持稳定,则需满足: (30) (31) 将式(31)拆成如下两部分: (32) (33) (34) (35) 因此,通过式(23)和式(35)辨识过程完全稳定后,则可得到定子电阻、定子电感和转子磁链的辨识值,该辨识值就是式(7)中定子电阻实际值Rs0、定子电感实际值L0和转子磁链实际值ψf0。 本文研究重点在于电机参数失配对无差拍电流预测算法的性能影响及如何进行改进。针对提出新型模型参考自适应系统的参数分步辨识来改进无差拍电流预测控制,通过实验的方法来验证其有效性。本文采用id=0的矢量控制,图4为改进后的无差拍电流预测控制系统结构框图。 图4 改进后的无差拍电流预测控制系统结构框图Fig.4 Structure block diagram of improved DPCC system 本次实验使用意法半导体ST公司的STM32F417作为电机控制器的主控芯片,6个半桥臂采用安世半导体nexperia的BUK9M35-80E,实验用400 W的表贴式永磁同步电机,其参数如表1所示,本次实验平台搭建如图5所示。实验过程分为三个阶段,首先进行无差拍电流预测控制器参数和电机参数不匹配的性能实验,观察电机参数失配对性能的影响;其次进行新型模型参考自适应系统的参数分步辨识实验,观察基于该方法下的参数精度;最后将新型模型参考自适应辨识好的参数给入无差拍电流预测控制进行实验,与电机参数同时失配的性能影响进行对比,得出改进后的结论。 图5 实验平台搭建Fig.5 Construction of experimental platform 4.2.1 转子磁链单独失配的影响 图6为转子磁链在0.5倍和1.5倍失配下d-q轴电流启动响应波形。 图6 转子磁链失配下d-q轴电流启动响应波形Fig.6 d-q axis current start response waveform under rotor flux linkage mismatch 4.2.2 定子电感单独失配的影响 图7 定子电感失配下d-q轴电流启动响应波形Fig.7 d-q axis current start response waveform under stator inductance mismatch 4.2.3 定子电阻单独失配的影响 4.2.4 电机参数同时失配的影响 图9为电机参数在0.5倍和1.5倍同时失配下d-q轴电流启动响应波形,其中电机参数分别为转子磁链,定子电感和定子电阻。实验条件给定2 500 r/min的转速启动运行,其中图9(a)为Rs0=0.5Rs,ψf0=0.5ψf,L=0.5L0同时失配下的d-q轴电流启动响应波形,通过与图6(b)、图7(a)、图8(b)相比,实际电流iq在稳态过程中产生了更大的跟踪静差,实际电流id在稳态过程中产生了一定的跟踪静差,实际电流iq的动态跟踪性更差。其中图9(b)为Rs0=1.5Rs,ψf0=1.5ψf,L=1.5L0同时失配下的d-q轴电流启动响应波形,通过与图6(a)、图7(b)、图8(a)相比,实际电流iq在稳态过程中产生了更大的跟踪静差,实际电流id在稳态过程中产生了一定的跟踪静差,实际电流iq的动态跟踪性更差。由上述实验结果可知,电机参数同时失配会对动态跟踪性和鲁棒性造成严重影响。 图9 电机参数同时失配d-q轴电流启动响应波形Fig.9 d-q axis current start response waveform under simultaneous motor parameters mismatch 图10为新型模型参考自适应的参数分步辨识波形,表2为辨识结果总结。实验条件给定2 500 r/min的转速启动运行,由图10和表2可知,由于电机起步阶段的不稳定性,导致辨识的电机参数发生了一定的超调,但是经过调节后迅速趋于稳定。其中图10(a)为转子磁链辨识波形,可知转子磁链在30 ms左右开始辨识,辨识结果经过1.5 ms左右的调节时间收敛于0.25 Wb左右,得到的最大误差为3.2%。其中图10(b)为定子电阻和电感同时参数辨识波形,可知定子电感和电阻同时在42 ms左右开始辨识,定子电感辨识结果经过2 ms左右的调节时间收敛于10.2 mH左右,得到的最大误差为2.3%,定子电阻辨识结果经过2.7 ms左右的调节时间收敛于0.15 Ω左右,得到的最大误差为2.5%。由上述实验结果可知,基于新型模型参考自适应的参数分步辨识算法可以在较短时间内收敛到参数给定值附近,并且最大误差很小,达到了很好的参数辨识效果。 表2 辨识结果总结Table 2 Identification result summary 图10 新型模型参考自适应的参数分步辨识波形Fig.10 Parameter stepwise identification of new MRAS waveform 图11 参数分步辨识下的无差拍电流预测控制波形Fig.11 DPCC waveform under parameter stepwise identification 本文的实验数据仅限于此次实验搭建的平台,而本次实验电机参数辨识开始时的超调如何减小,有待进一步研究与分析。 以400 W的表贴式永磁同步电机为研究对象,本文针对参数失配会导致无差拍电流预测控制的动态跟踪性和鲁棒性差的问题,提出一种基于新型模型参考自适应系统的参数分步辨识来进行改进,通过实验验证分析可以得到以下结论: 1)电机参数失配会对无差拍电流预测控制产生一定的影响,包括:动态跟踪效果差、跟踪静差大和鲁棒性差,为后面进行改进提供了实验依据; 2)通过新型模型参考自适应系统设计出参数分步辨识法,经过相关实验验证出此方法的辨识结果精度高; 3)将上述得到的参数辨识结果给入设计好的无差拍电流预测控制中,可以有效地抑制参数失配带来的影响,减小了跟踪静差,提高了系统的动态跟踪效果,同时增强了系统在负载突变下的鲁棒性。 实验结论表明,基于新型模型参考自适应系统的无差拍电流预测控制具有一定的实用性,但是本文实验中参数辨识开始时的超调如何减小,有待进一步探究。2 新型模型参考自适应的参数分步辨识思想
2.1 传统模型参考自适应系统的参数辨识
2.2 新型模型参考自适应系统的参数分步辨识
3 参数分步辨识实现
3.1 转子磁链的辨识实现
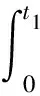


3.2 定子电阻和定子电感的辨识实现
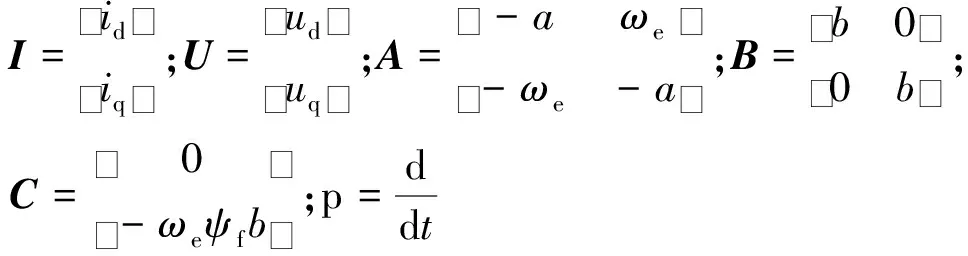
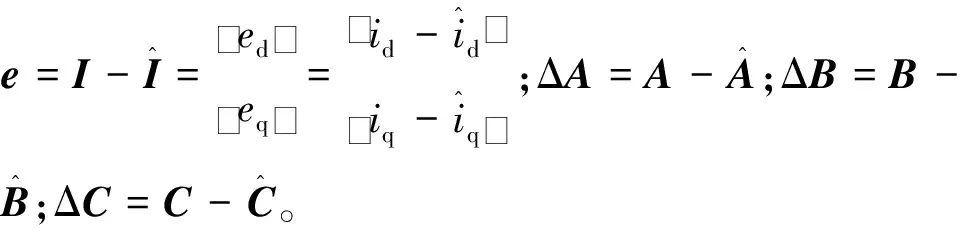

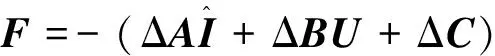
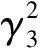
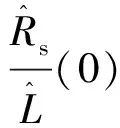
4 实验结果及分析
4.1 实验平台搭建

4.2 验证电机参数失配对无差拍电流预测控制的性能影响

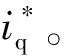
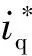
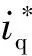
4.3 验证基于新型模型参考自适应的参数分步辨识精度
4.4 验证基于参数分步辨识算法下的无差拍电流预测控制性能
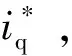

5 结 论

