水轮发电机机电故障的轴电压特征分析及诊断
李剑立, 武玉才, 卢伟甫
(1.华北电力大学 河北省绿色高效电工新材料与设备重点实验室,河北 保定 071003; 2.国网新源控股有限公司技术经济研究院,北京 100761)
0 引 言
水轮发电机在运行过程中,受静电效应、磁路不对称、单极效应、静态励磁等因素影响,在机组转轴对地、转轴两端、轴颈两端产生电位差,称之为轴电压[1-2]。
水轮发电机偏心故障及匝间短路故障所致磁路不对称是轴电压最常见的诱因之一。偏心故障包含动偏心和静偏心,通常是由转轴弯曲、质量不平衡、安装精度、轴承磨损、共振等原因引起的[3-4],2种偏心故障的共同特点是转子中心偏离了发电机中心,其中,动偏心故障下转子中心围绕发电机中心旋转,静偏心故障下转子中心围绕自身中心旋转[5-6]。匝间短路故障普遍存在于水轮发电机中,由于水轮发电机极对数相对较多、结构为凸极结构且定子绕组分支数较多,若机组某一磁极发生转子绕组匝间短路,对磁极局部电磁量影响较大,对机组本身而言影响较小。
截止目前,学者们对发电机机电故障进行了大量研究,文献[7]提出了利用固定在定子内侧的无源传感器和磁极之间的电容电流测量气隙,对水轮发电机偏心故障进行诊断。文献[8]提出通过测量超声波在定子和转子之间的传播时间来监测偏心,将气隙监测传感器安装在一台170 MW水轮发电机上进行气隙动态监测。文献[9]介绍了一种基于电感式传感器的水轮发电机气隙监测系统,可以实时判断转子静态或动态偏心量、定子或转子变形量及绕组匝间短路量。文献[10]仿真发现定子和转子电流中特定谐波可以作为转子偏心故障的判据。文献[11]提出了一种基于环流特性的气隙偏心与转子绕组匝间短路复合故障诊断方法。文献[12]利用多回路法分析故障前后励磁电流的变化,用于诊断水轮发电机转子绕组匝间短路。文献[13]利用水轮发电机的气隙磁通密度确定了安装在电机气隙中的霍尔传感器位置和数量,根据空载和负载时气隙磁通密度不同,来检测匝间短路故障严重程度和故障位置。文献[14]在机组的2个不同位置安装感应探针,利用磁路对称原理检测大型水轮发电机转子绕组匝间短路。文献[15]根据磁动势平衡原理,提出在水轮发电机定子铁心上安装U型检测线圈,用以检测转子绕组匝间短路故障,并能定位故障磁极位置。
转子是电机磁路的一个重要部分,电机相关故障会在磁场方面反映,并通过电磁感应作用在转子上感应轴电压[16-17]。因此,学者们开始尝试通过轴电压对发电机故障进行诊断[18]。文献[19]提出基于轴电压特征信号监测汽轮发电机转子匝间短路故障以及发电机定子接缝不对称。文献[20]经过实践提出通过轴电压诊断气隙不对称、转子绕组匝间短路故障的方法。文献[21]考虑了静偏心故障时定子槽和电枢绕组对轴电压的影响,实验结果表明静偏心会产生频率为50 Hz的基波轴电压,并伴随三次谐波轴电压。文献[22]针对隐极同步发电机转子偏心和转子绕组匝间短路故障,采用气隙磁导法分析电机气隙磁场,推导得到故障引起的畸变磁场特征量,特征频率为kω/p(k=1,2,3,…),实验证明轴电压可用于诊断隐极同步发电机转子偏心和转子绕组匝间短路故障。
本文以抽水蓄能电站一台334 MVA水轮发电机为研究对象,首先建立发电机磁势和磁导模型,通过理论分析预测静偏心故障及匝间短路故障引起的畸变磁通特征,进一步通过有限元仿真模拟机组静偏心故障和匝间短路故障,提取轴电压波形,分析表明该轴电压的主要频率与理论推导吻合,证明轴电压可用于水轮发电机转子典型故障判断。
1 考虑偏心下的磁场分布
水轮发电机正常运行时,气隙合成磁动势可以分解为一系列奇数次谐波磁动势之和,对于p对极的水轮发电机磁动势可以表示[23]为
(1)
式中:k为正奇数;p为水轮发电机的极对数;Fk为第k次谐波磁动势的幅值;θs为定子空间角;ωr为转子机械角速度;φk为k次谐波磁动势的相位。
水轮发电机转子为凸极结构,气隙不均匀,由于动偏心已被证实无法形成轴电压,故此处仅考虑静偏心,发电机气隙磁导λ(θs,t)可以表示[24]为
(2)
式中:λ0为常数;λ2i为气隙磁导的2i次谐波幅值;λg为气隙磁导的g/p次谐波幅值;φsg为相对静偏心第g次谐波磁导的初始相位;i、g均为正整数。
由式(1)、式(2)的磁动势及气隙磁导,发电机气隙磁通密度可以表示为
B(θs,t)=F(θs,t)λ(θs,t)=
(3)
1.1 凸极项
受凸极结构引起的气隙磁通密度Bi(θs,t)表达式为
2ip(θs-ωrt)]+cos[kp(θs-ωrt-φk)+
{cos[(kp-2ip)(θs-ωrt)-kpφk]+
cos[(kp+2ip)(θs-ωrt)-kpφk]}。
(4)
由于k为正奇数,2i为正偶数,两者不存在相等情况,此时磁通转速为dθs/dt=ωr,与转子同步速旋转,可看作极对数为(k-2i)p与(k+2i)p的机组气隙磁通密度。
1.2 静偏心
静偏心引起的气隙磁通密度Bg(θs,t)为
{cos[kp(θs-ωrt-φk)-g(θs+φsg)]+
cos[kp(θs-ωrt-φk)+g(θs+φsg)]}=
kp(ωrt+φk)-gφsg]+cos[(kp+g)θs-
kp(ωrt+φk)+gφsg]}。
(5)
式(2)中g为正整数,存在kp-g=0的情况,此时式(5)中出现Fkλg[kp(ωrt+φk)+gφsg]/2这一分量,该项不含θs,与定子空间角度无关,围绕转子圆周均匀分布、仅随时间正弦变化,不满足磁通连续性定理,该部分磁通畸变为环绕转轴的交变磁通,又由ωr=ω/p得,角频率为kpωr=kpω/p=kω,可以判断机组受静偏心故障影响,交变磁通中出现了50kHz(k=1,3,5,…)的特征量。
其次讨论kp-g≠0的情况,此时旋转磁场转速为dθs/dt=kpωr/(kp-g)与dθs/dt=kpωr/(kp+g),与转子之间存在相对运动,在转子表面产生涡流损耗。
2 转子绕组匝间短路下的磁场分布
当水轮发电机某一极发生匝间短路故障,磁动势可视为转子绕组正常时的磁动势与被短路匝通入反向电流时的磁动势之和[26],下文分析机组发生匝间短路时的磁场分布。
当机组发生匝间短路时,被短路匝通入反向电流时的磁动势[25]为
(6)
式中:ΔFn=2QIfsin(nα/2)/(πn);n为正整数;Q为短路匝数;If为励磁电流;α为跨距。
此时的气隙磁通密度为
ΔB(θs,t)=ΔF(θs,t)λ(θs,t)=
(7)
2.1 凸极项
考虑到式(6)中n为正整数,分析其磁场分布,受凸极结构引起的气隙磁密ΔBi(θs,t)表达式为

2ip(θs-ωrt)]+cos[n(θs-ωrt)+
{cos[(n-2ip)(θs-ωrt)]+
cos[(n+2ip)(θs-ωrt)]}。
(8)
与式(1)中k为正奇数不同,式(6)中n为正整数,此时存在n-2ip=0的情况,当n-2ip=0时,式(8)中出现ΔFnλ2icos(θs-ωrt)/2这一分量,该部分磁通畸变为环绕转轴的交变磁通,又由ωr=ω/p得,nωr=nω/p,将n=2ip带入可得,角频率为2iω,可以判断在匝间短路情况下,受凸极项影响,出现50×2iHz(i=1,2,3,…)的特征量。
当n-2ip≠0时,旋转磁场转速为dθs/dt=ωr,与转子同步速旋转,不存在相对运动,可看作极对数为n-2ip与n+2ip的机组气隙磁通密度。
2.2 静偏心
匝间短路发生之后,静偏心引起的气隙磁通密度ΔBg(θs,t)为
g(θs+φsg)]+cos[n(θs-ωrt)+
{cos[(n-g)θs-nωrt-gφsg]+
cos[(n+g)θs-nωrt+gφsg]}。
(9)
当n-g=0时,式(9)中出现ΔFnλgcos(nωrt-gφsg)/2这一磁通分量,该分量缺少θs,不随定子空间角度变化而变化,仅随时间正弦变化。同样违背磁通连续性定理,磁通分量发生了畸变,其角频率为nωr=nω/p,特征频率为50n/pHz(n=1,2,3,…)。由式(5)分析可得,机组在静偏心影响的正常状况下,交变磁通中出现了50kHz(k=1,3,5,…)的特征量。不难看出,后者为前者的真子集,故在静偏心状态下发生转子绕组匝间短路对应特征频率为50n/pHz(n=1,2,3,…且n/p≠1,3,5,…),即为分数次或偶数次谐波,不难预测,在极对数为9的水轮发电机中,特征频率为50n/9 Hz。
当n-g≠0时,式(9)分析与式(5)分析类似,不再展开讨论。
转子静偏心引发的轴电压特征频率与转子绕组匝间短路引发的轴电压特征频率是不同的,二者轴电压的产生原因、故障部位以及特征频率如表1所示。

表1 轴电压产生原因、部位和特征频率
3 有限元仿真验证
本文采用一台334 MVA水轮发电机为研究对象,采用ANSYS软件建立发电机二维仿真模型,水轮发电机参数如表2所示。
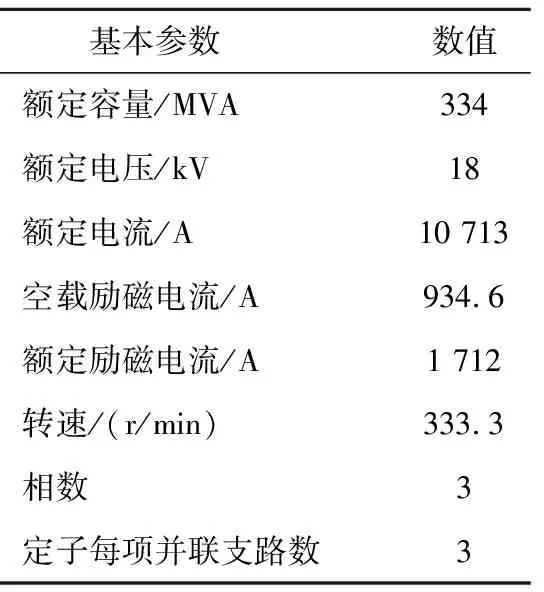
表2 水轮发电机参数Table 2 Power operating parameters of hydro-generator
通过ANSYS-maxwell搭建二维有限元仿真模型,如图1所示。并将模型导入ANSYS-simplorer,按照定、转子实际连接情况搭建机组场路耦合瞬态仿真模型,如图2所示。

图1 水轮发电机二维有限元模型Fig.1 Two-dimensional finite element model of hydro-generator
仿真获得334 MVA水轮发电机空载和额定负载工况的径向磁通密度,如图3所示,定子电压和电流如图4、图5所示。
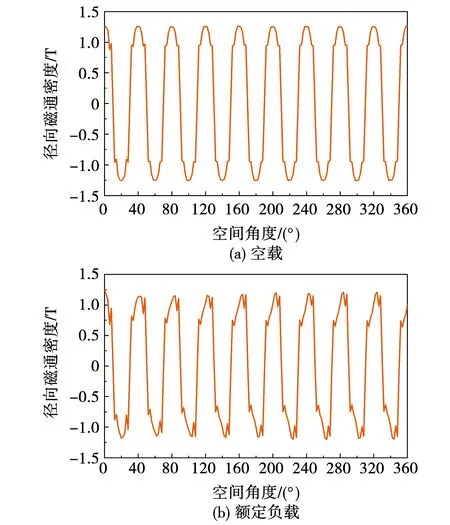
图3 水轮发电机径向磁通密度Fig.3 Radial flux density of hydro-generator
分别对水轮发电机进行空载和额定负载仿真,得到的轴电压时域图如图6所示。
图6(a)为正常状态空载波形图,图6(b)为正常状态额定负载波形图。受齿槽效应及考虑实际工况中定子铁心叠片接缝,空载及额定负载状态存在不同程度的轴电压。
图7(a)为水轮发电机空载状态下发生不同程度静偏心时的轴电压波形,图7(b)为与图7(a)对应的局部放大图,图8(a)为额定负载不同程度静偏心轴电压波形,图8(b)为图8(a)对应的局部放大图。可以看出,偏心程度逐渐增加时,空载状态下轴电压幅值逐渐增大,且额定负载状态下轴电压幅值也逐渐增大,两者变化均为同向变化。

图7 空载状态静偏心轴电压波形图Fig.7 Waveform of static eccentric shaft voltage in no-load state
图9(a)为水轮发电机空载状态下静偏心程度为15%时,1号磁极发生3,6,9匝等不同程度短路的轴电压波形图,图9(b)为与图9(a)对应的局部放大图,图10(a)为额定负载状态下静偏心程度为15%,1号磁极发生3,6,9匝等不同程度短路的轴电压波形图,图10(b)为图10(a)对应的局部放大图。可以清晰地看出,随着短路程度逐渐增加时,空载状态下轴电压幅值逐渐增大,且额定负载状态下轴电压幅值也逐渐增大,两者变化均为同向变化。
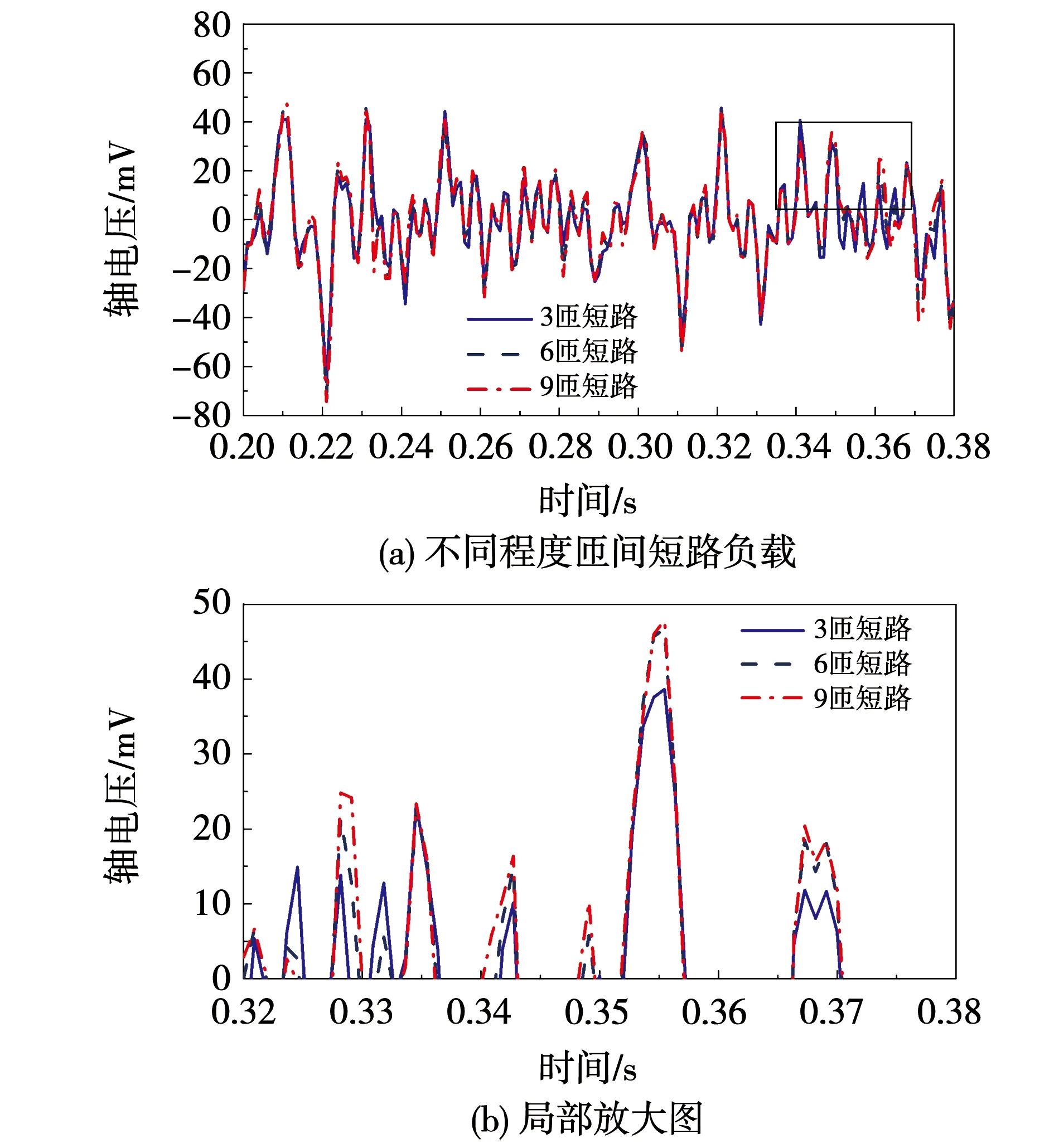
图10 负载状态短路轴电压波形图Fig.10 Load state short-circuit axis voltage time waveform
水轮发电机的转子静偏心故障及绕组匝间短路故障,随着静偏心或匝间短路程度的加重,轴端感应电压的幅值也将变大,因此,该方法还可以反映出静偏心及绕组匝间短路故障的严重程度和发展趋势。
图11(a)、 (b)为空载状态下静偏心程度0、15%、30%、45%的轴电压频域图,图11(c)、 (d)为额定负载状态下静偏心程度0、15%、30%、45%的轴电压频域图。空载及额定负载状态下均出现了50、150、250 Hz,…等特征频率,与式(6)分析结论中50kHz(k=1,3,5,…)的特征量吻合。

图11 不同程度静偏心轴电压频域图Fig.11 Voltage frequency domain diagram of different degrees of static eccentric shaft
不同程度匝间短路轴电压频谱图如图12所示,图12(a)为空载状态下静偏心程度15%且1号磁极发生0、3、6、9匝短路的轴电压频谱图,图12(b)为额定负载状态下静偏心程度15%且1号磁极发生0、3、6、9匝短路的轴电压频谱图。可以观察出,空载与负载状态下,8×50/9、26×50/9、46×50/9 Hz也即44.4、144.4、255.5 Hz等特征频率较为明显,与式(11)分析结论中50n/pHz(n=1,2,3,…且n/p≠1,3,5,…)特征频率相吻合。所分析的水轮发电机极对数p=9,因此上述的分数次谐波即为机组在偏心状态下发生间短路所产生的特征量。
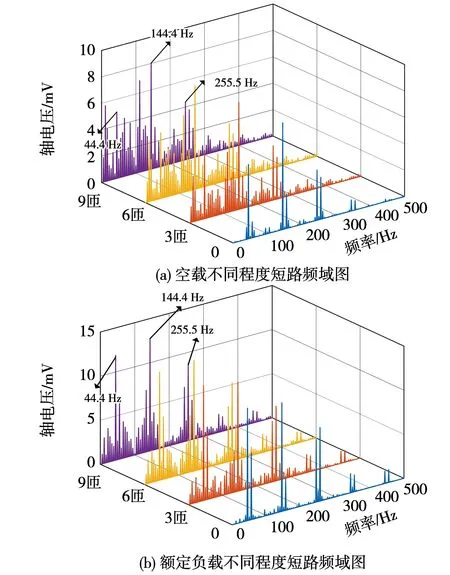
图12 不同程度匝间短路轴电压频谱图Fig.12 Voltage spectrum of axis with different degrees of inter-turn short circuit
轴电压频率与畸变磁通密度频率一致,幅值随着偏心或短路程度同向变化。因此,可以通过轴电压诊断发电机转子机电故障。
4 结 论
本文分析了水轮发电机转子机电故障的磁场特征分布,并通过有限元仿真了机组的轴电压,得出以下结论:
1)机组发生静偏心时,轴电压频率中出现了50kHz(k=1,3,5,…)的特征量,且不受机组极对数影响。
2)静偏心所引发的轴电压特征频率与其他原因引发的轴电压特征频率是不同的,其特征频率为50kHz(k=1,3,5,…),因此可以有效识别故障的发生。
3)机组在偏心状态下发生转子绕组匝间短路时,轴电压特征频率为50n/pHz(n=1,2,3,…且n/p≠1,3,5,…),即为分数次或偶数次谐波。因此可以根据该特征频率判断偏心状态下机组是否发生转子绕组匝间短路。
轴电压可作为水轮发电机转子故障检测与判别的信号,为水轮发电机转子故障判别提供了新的方案。

