虚拟阻容下的LCL型并网逆变器谐振抑制策略
张继红, 刘云飞, 卢星升, 赵锐, 吴振奎, 张晓明
(内蒙古科技大学 信息工程学院,内蒙古 包头 014010)
0 引 言
为实现我国“碳达峰、碳中和”的既定目标、缓解化石能源枯竭危机,构建“安全、绿色、高效”的清洁能源系统,新能源发电已进入大规模开发应用阶段[1-3]。目前,在该领域中仍以风能、光伏等分布式发电应用最为广泛,并受到能源专家的日益广泛关注[4]。逆变器作为分布式电源并网的核心模块,在电能变换中发挥了重要作用[5]。而滤波器是保证电能质量的关键器件,是逆变电路的重要组成部分。由于LCL滤波器具有体积小、重量轻,成本低廉等突出优势,所以该类型滤波器应用最为广泛[6-7]。然而,规模化的新能源发电方式采用多逆变器并联进行扩容和备用,从而引发了滤波器储能元件的谐振问题不可避免,甚至影响了逆变器稳定运行。例如,单台LCL滤波器为三阶系统,运行过程中将产生谐振峰值;多台LCL滤波器并联运行还会因相互耦合导致并联谐振和串联谐振发生。谐振的产生不仅降低了供电电能质量,而且会导致设备崩溃、并网失败等连锁反应,对于供电的可靠性和安全性构成极大威胁[8-11]。基于新能源的快速发展和大规模电力电子器件参与电能变换场景日益普遍,谐振对于今后高渗透率新能源发电情形将构成较大不利影响,因而逆变器并网谐振问题的抑制已成为近年来科学研究的热点[12]。
文献[13]提出基于自适应滤波的谐振抑制策略,借助最小均方算法对系统进行预测和控制,虽然能够达到抑制谐振的目的,但算法过程繁琐,不利于实际工程应用。文献[14]提出补偿虚拟阻抗相角偏移,恢复虚拟阻抗的正阻尼控制策略,然而实际应用中的相角补偿环节大多为超前环节,这样容易放大高频谐波。文献[15]建立了共模数学模型,通过控制共模阻抗的方式抑制谐振,但针对闭环条件下系统的抑制效果不够理想。文献[16]提出了基于滤波器前馈的有源阻尼方法,该方法谐振抑制效果明显,但会改变控制带宽,不利于系统的稳定运行。文献[17-18]从逆变器自身谐振、并联谐振和串联谐振三个方面进行了分析,分别提出了滤波电容并联虚拟电导和虚拟电阻的谐振抑制策略,但未考虑逆变器不等容、滤波器参数不一致情况下的谐振抑制问题。
本文通过构建逆变器并联系统模型分析滤波器自身谐振、并联谐振和串联谐振的产生机理及相互耦合关系,借鉴自动控制理论获得闭环系统结构并得到传递函数,研究基于下垂控制算法的虚拟电容控制策略,分析滤波效果。通过引入虚拟电阻,研究虚拟参数的选取与稳定性的关系,借助电感电压反馈降低系统阶次,优化系统模型,达到良好的谐振抑制效果。
1 多逆变器并联系统建模
本文搭建的多LCL型三相并联逆变器系统模型如图1所示,图中:Lk1(k=1)(下同)表示逆变侧电感;Lk2表示网侧电感;Ck表示滤波电容;Lg表示电网电感;udc表示直流侧电压;uin表示逆变器输出电压;upcc表示公共耦合点电压;uck表示滤波电容电压;ik1表示逆变器输出电流;ik2表示并网电流;ig表示电网电流。
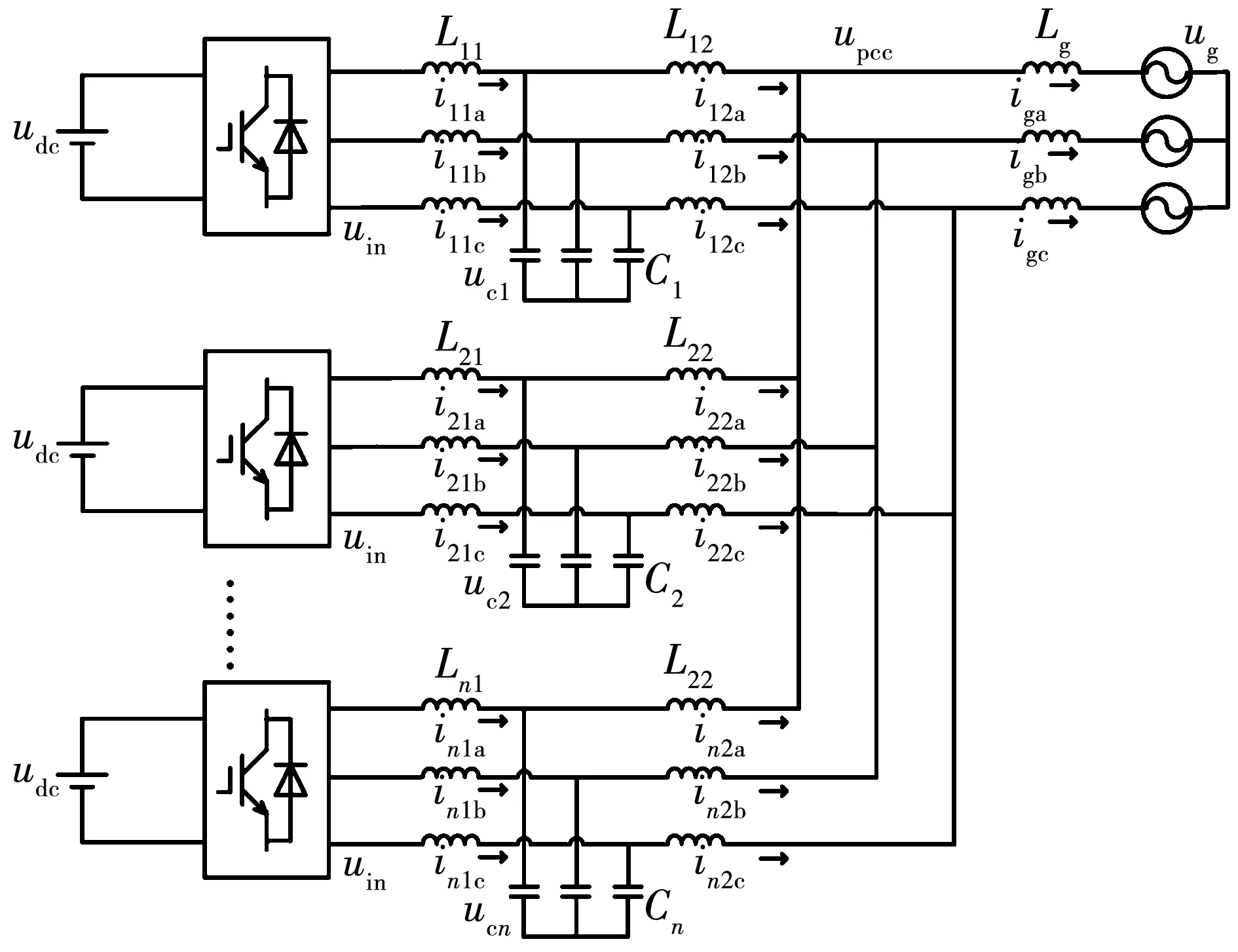
图1 多逆变器并联结构示意图Fig.1 Diagram of multi-inverters parallel system
为简单起见,首先建立单台并网逆变器闭环系统控制结构如图2所示。图中:i1ref表示第一台逆变器给定电流;KPWM为逆变器增益。

图2 闭环控制框图Fig.2 Block diagram of dual closed-loop control
考虑到不同容量逆变器并联情况下可能会受到环流影响,因本文滤波器选用LCL滤波器,使得主要的环流成分为零序环流,该环流易引发系统损耗和电流应力不足等问题,进而降低系统稳定性,不利于良好的谐振抑制效果。故选用准PR控制器代替PI控制器对零序环流进行抑制,准PR控制器表达式为
(1)
式中:kp为控制器比例系数;kr为谐振系数;ωr决定系统频率带宽大小,考虑到控制器的计算精度要求,ωr在π到10π间取值,此处ωr=5,兼顾系统稳定性和鲁棒性的情况下选取kp=4,kr=150。
据图3可知,准谐振控制器在工频处的增益高于PI控制器,因此,准谐振控制可实现电流信号更准确的无静差跟踪。消除与谐振频率相同频率的扰动分量对闭环系统的影响。此外,相对于PI控制器而言,准谐振控制器对逆变器等效输出阻抗的感性分量抵消效果更好,在具备高增益的同时,还可以扩大输出阻抗的频宽,即使在高频阶段也可保持阻性状态,减少逆变器间输出偏差抑制环流[19-21]。
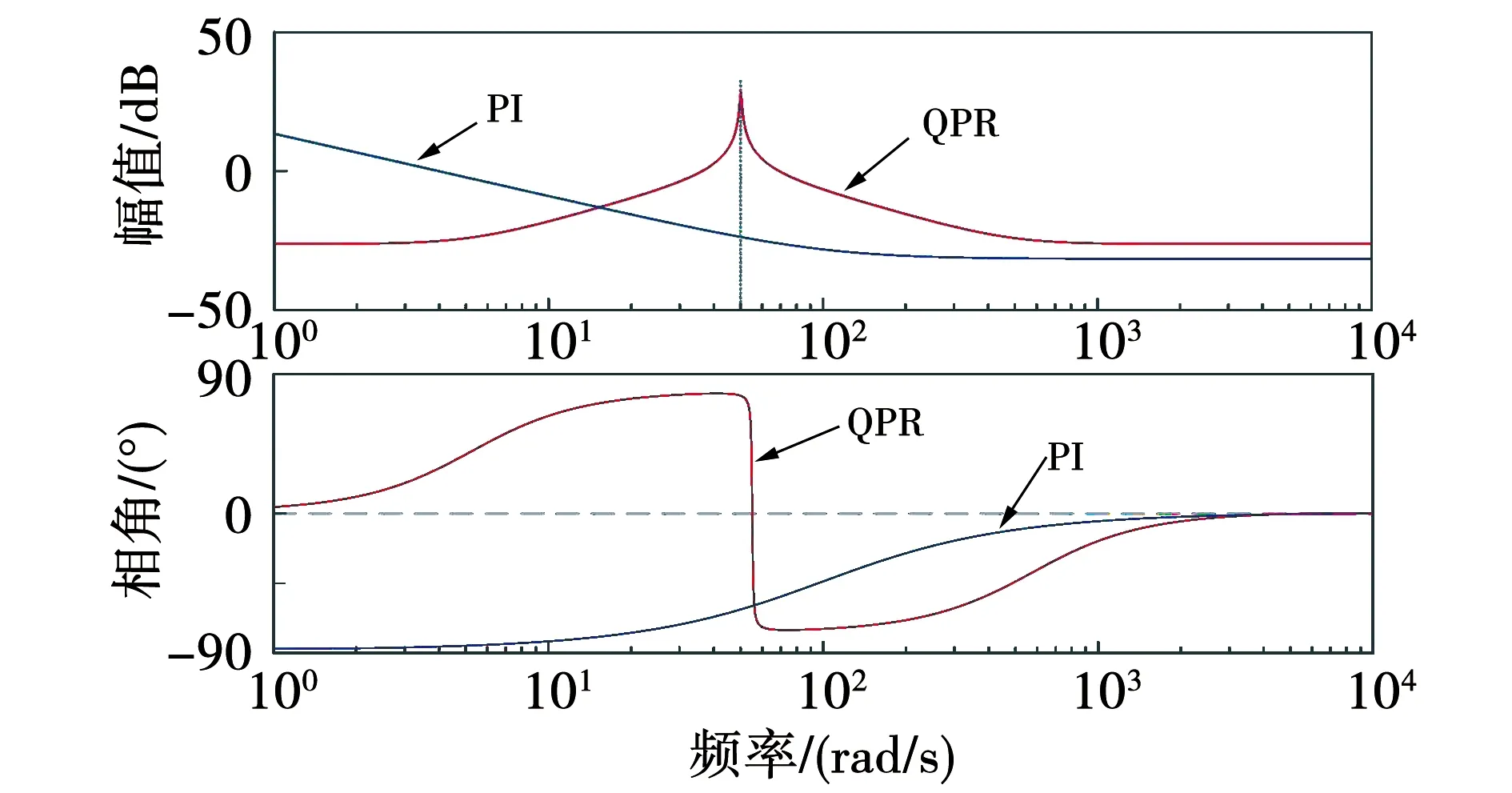
图3 控制器幅频特性对比Fig.3 Comparison of controller amplitude and frequency characteristics
由图2可得并网电流表达式为
i12(s)=G11(s)i1ref(s)-G12(s)upcc(s)。
(2)
式中:
(3)
式中:G1.1表示并网电流与给定电流间传递函数;G1.2表示并网电流和公共耦合点电压间传递函数。A表示系统特征方程。将单台逆变器结构图进行推广得到多台逆变器并联运行情况,并根据系统结构和传递函数关系可得n台逆变器并联运行的诺顿等效电路,如图4所示。

图4 多逆变器并联等效电路图Fig.4 Parallel equivalent circuit diagram of multiple inverters
由图4可得,第1台逆变器并联数学模型为
(4)
GY(s)i1ref(s)-GB(s)upcc(s)。
(5)
将式(4)和式(5)联立消去upcc可以得到:
Gseries,1(s)ug(s)。
(6)
设n台逆变器型号和参数相同,则有G1.1=GY,G1.2=GB。第一台逆变器自身谐振、并联谐振、串联谐振表达式为:
(7)
由式(6)、式(7)可知,并网电流主要由该逆变器给定电流、其他逆变器给定电流以及电网电压决定。各自之间的耦合关系分别表示为Gself,1、Gpara,k,1和Gseries,1,即为各自传递函数表达式。
2 多逆变器并联谐振产生机理及特性分析
由式(7)传递函数得到n分别取1、2、3、4、5时逆变器的谐振幅频特性曲线。LCL滤波器在滤除高次谐波的同时也会将其欠阻尼三阶系统特性引入并联系统,这是产生自身谐振的根本原因。根据图5可知:当逆变器台数为单台时,自身谐振曲线只有一个谐振峰;当逆变器台数n≥2时,自身谐振曲线出现两个谐振峰,其中低频谐振峰的频率随着逆变器台数增加而不断减小,且峰值也会随之降低。高频谐振峰的频率不会随着逆变器台数变化而变化,峰值固定不变,且高于低频谐振峰峰值。
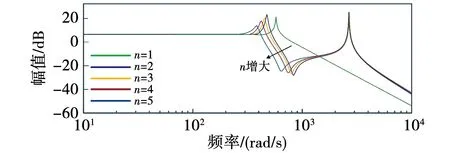
图5 Gself,1幅频特性曲线Fig.5 Gself,1 amplitude-frequency characteristic curve
任一逆变器参考电流的阶跃变化都会引发并联谐振的产生。根据图6可知:并联谐振曲线同样存在两个谐振峰,低频谐振峰的频率和峰值也会随着逆变器台数的增加呈下降趋势;高频谐振峰频率变化情况与自身谐振相同,但峰值会随逆变器台数增加而降低。
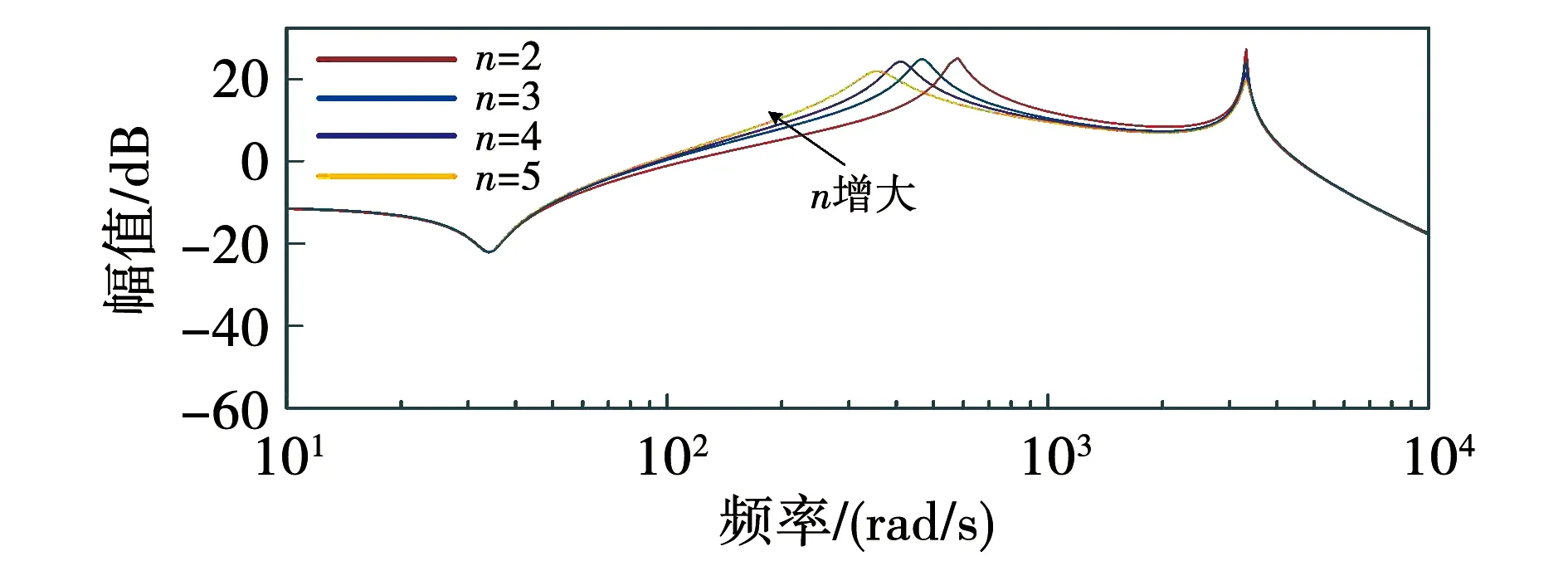
图6 Gpara,k,1幅频特性曲线Fig.6 Gpara,k,1 amplitude-frequency characteristic curve
串联谐振的产生主要归结为电网相关参数和背景谐波的影响,此外控制器和滤波器参数也会发挥一定作用。根据图7可知:串联谐振曲线只存在一个谐振峰,其频率随逆变器台数增加呈下降趋势,峰值也会降低。
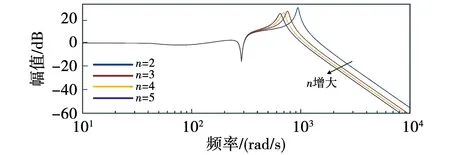
图7 Gseries,1幅频特性曲线Fig.7 Gseries,1 amplitude-frequency characteristic curve
3 有源谐振抑制策略
通过对LCL型逆变器谐振机理的分析不难看出,产生谐振的主要原因在于其闭环传递函数为欠阻尼特性。所谓欠阻尼,是以阻尼率ζ为标准进行划分,当0<ζ<1时微分方程的解为一对实部为负的共轭复根,系统时间响应具有振荡特征,称为欠阻尼状态。届时,阻尼并不足以阻止振动越过平衡位置,系统将产生阻尼振动[22-23]。
本文重点从谐振产生原因入手,提出虚拟电容、电阻混合控制策略,以增强滤波性能、增大阻尼,实现谐振抑制,在此基础上考虑欠阻尼三阶系统特性作用,补充添加电感电压前馈控制对系统进行降阶处理,以此抑制自身谐振,巩固系统稳定性。
3.1 虚拟电容设计原理

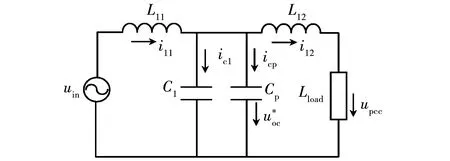
图8 并联虚拟电容等效电路图Fig.8 Parallel virtual capacitor equivalent circuit diagram
采用基尔霍夫电压定律分析等效电路可得到电压、电流关系,如下:
uin-sL11i12-sL11ic1-sL11icp=
uin-s2L11uoc(Cp+C1)-sL11i12;
(8)
u1v=uin-s2L11uoc(Cp+C1)。
(9)
因两电容为并联关系,电压相等,因此可将两电容统一分析,其中,uoc表示并联虚拟电容前支路电压,进而得出虚拟电容的指令电压u1v。
将上式变换到交-直二维坐标,得到虚拟电容算法的结构框图如图9所示。
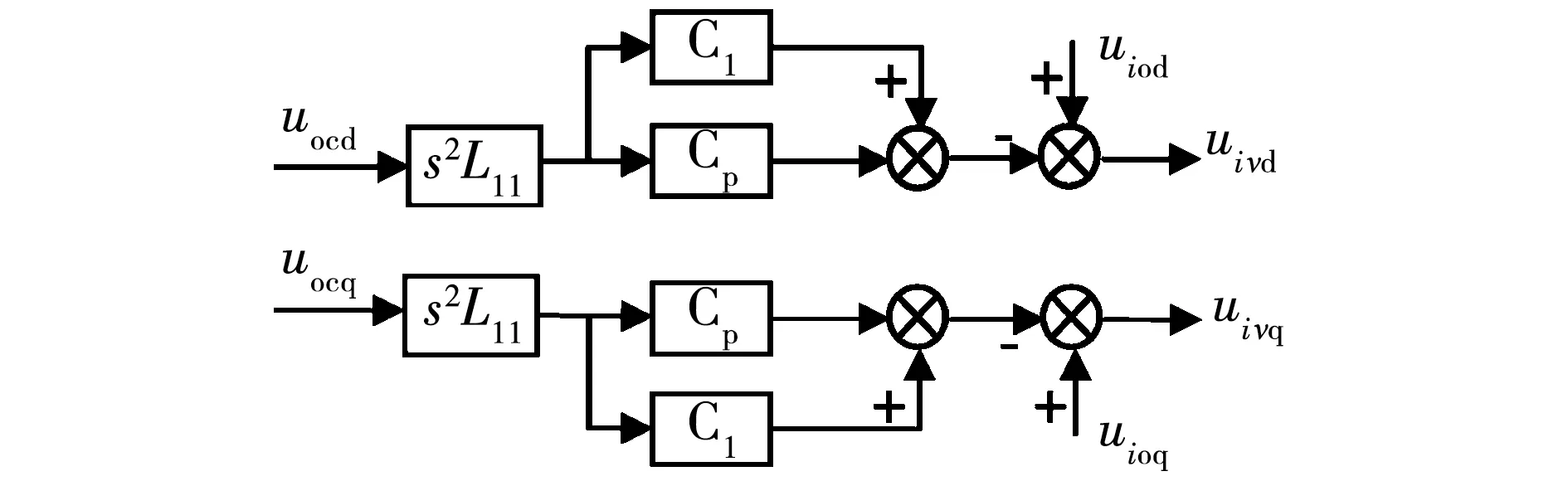
图9 虚拟电容结构框图Fig.9 Block diagram of virtual capacitor structure
图9中,uocd、uocq参考发电机下垂特性设计,理论计算过程如图10所示。由滤波电容电压和逆变器输出电流作为功率环节输入,P、Q分别为逆变器输出有功、无功功率;P*、Q*分别表示有功功率和无功功率的参考值;m、n分别为频率和电压下垂增益;f0、U0分别为逆变器输出电压额定频率和幅值;fref、Uref分别为输出电压频率和幅值的参考值。

图10 下垂控制框图Fig.10 Block diagram of sag control
虚拟电容的设计虽然可以提升高次谐波的滤除能力,但该方式只是间接对并网电流进行控制,滤波器件参数具有不确定性,对谐振的抑制效果不够理想,因此同样有谐振存在。
3.2 虚拟电阻值设计
为弥补上述控制的不足,采用虚拟电阻串联虚拟电容策略抑制谐振,该方法可以对谐振起到直接抑制的作用,且不会产生额外损耗,加入虚拟电阻Rp后的并网电流表达式为
(10)
(11)
将式(11)进行推广,可以得到n台逆变器并联运行下新的并网方程为
(12)
加入虚拟电阻后既要保证谐振可以得到有效的抑制,也要保证系统稳定性能。阻尼的增加有利于补偿系统的有效阻尼,但过大会造成系统波动,过小的阻尼易出现频率偏差出界,甚至导致系统性能变差。此外,虚拟电阻还会影响单位功率因数。需要对虚拟电阻取值进行优化,设计的步骤如下。
首先,令虚拟电阻满足下式:
(13)
其次,以n=5为例进行计算,可得Rp=136 Ω。图11为加入控制策略后的系统根轨迹变化,据图可知:当Rp<136 Ω时,对谐振可以起到良好的抑制作用,但会使低频衰减,且随着Rp的减小衰减愈发严重,从而降低基波电流的跟踪性能;当Rp>136 Ω时,系统会出现振荡现象,且Rp越大振荡越剧烈,最终导致系统运行不稳定。Rp=136 Ω时,既可以保证抑制效果,又不会破坏系统的稳定性,是理想的取值。
3.3 计及系统降阶优化控制
逆变器自身谐振的主要原因在于滤波器的三阶系统特性,因此可从降低系统阶次入手达到抑制谐振的目的。考虑到通过零极点抵消降阶方法需要参数稳定和匹配,且受外界因素干扰适应性过低[24-25]。因此,引进逆变器侧电感电压反馈控制策略,该策略不受参数制约,有良好的降阶效果[26-27]。设计的控制框图如图12所示,u1为逆变器侧电感电压,Gf为电压反馈系数。

图12 综合控制框图Fig.12 Integrated control block diagram
如图12所示为添加电感电压前馈控制后的综合控制框图,利用逆变器侧电感电压反馈进行降阶,据图可得,引入电压反馈后的系统开环传递函数为:
T1=
(14)
(15)
由式(14)可知,当Gf=1/KPWM时可将式(14)可简化为
(16)
据式(16)可知,在不考虑GQPR影响的情况下,系统为一阶惯性环节,电压反馈使三阶系统降为一阶系统,原控制方式下的自谐振峰值被进一步抑制,稳定裕度得到了显著的提高,式(11)转换为下式:
(17)
最后,将式(17)代入式(12)绘制三种谐振的波形图进行分析。据式(15)可得n分别取1、2、3、4、5时的幅频特性曲线如图13、14、15所示。据分析可知:在加入抑制策略前,自身谐振高频最高峰值为24.6 dB,低频最高峰值为22.6 dB;并联谐振高频最高峰值为25.3 dB,低频最高峰值为23.7 dB;串联谐振峰值为27.1 dB。上述谐振峰值皆取最高谐振峰值。据抑制前后Bode图对比可知,高频谐振峰取得良好衰减效果的同时,低频谐振峰同样达到了理想衰减效果。都降至0 dB以下,尤其在高频段的阻尼效果非常明显,并且呈现持续衰减的趋势,说明所提控制策略可以对谐振起到较好的抑制作用。

图幅频特性曲线 amplitude-frequency characteristic curve
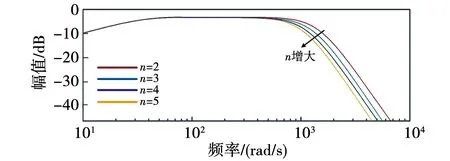
图幅频特性曲线图 amplitude-frequency characteristic curve
4 仿真算例设计
仿真实验中选取两种不同容量逆变器,并做同容量及不同容量逆变器并联情况分析,以验证所提策略在不同工况下对谐振的抑制效果。直流电压为700 V,电网相电压为220 V,电网等效电感为1 mH,其他系统参数见表1。
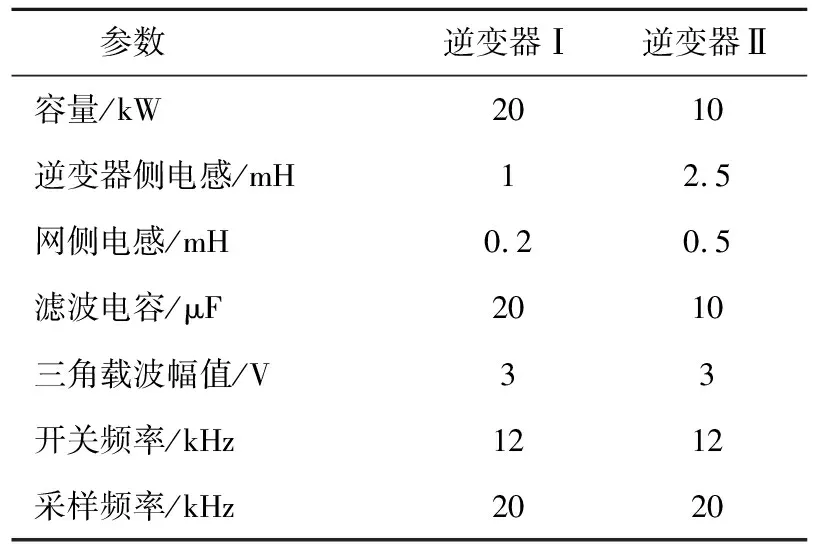
表1 并网逆变器参数Table 1 Grid-connected inverter parameters
4.1 同容量并联逆变器并网运行
将加入抑制策略前的并网电流和加入抑制策略后的并网电流进行对比,并网电流分为自身谐振电流、并联谐振电流和串联谐振电流,此外借助了MATLAB/Simulink中的FFT Analysis功能对并网电流畸变情况进行分析。
畸变率(THD)是谐波分析过程中的典型参数,畸变率的大小充分体现了电流波动情况,是电能质量优劣的指标参数,当THD<5%电流可平稳入网,系统保持稳定[28-30]。电流总谐波畸变率表示并网电流输出波形相对于正弦波的畸变程度,总谐波畸变率表达式为
(18)
各次谐波对电流畸变影响情况可由谐波电流含有率HRI表示,其表达式为
(19)
式中:Ih表示h次谐波电流的有效值;I1表示基波电流的有效值。
加入抑制策略前的自身谐振并网电流仿真结果如图16(a)、16(b)所示。由图可以看出自身谐振使并网电流产生畸变,由快速傅里叶变换分析结果可以得到:从整体分析并网电流谐波畸变率高达20.67%;分别从高频段和低频段观察可知,13次谐波和49次谐波的放大程度较为明显,各自为9.02%和18.70%。该仿真结果与图5自身谐振的幅频特性曲线呈现结果一致。将图16(a)、16(b)与图17(a)、17(b)对比可以发现,在引入抑制策略后并网电流的畸变情况得到有效改善,总畸变率下降到2.60%,13次谐波和49次谐波含有率分别下降为1.63%和0.72%。其中对高次谐波的抑制效果尤为明显,与图13分析相符。

图16 加入抑制策略前自身谐振并网电流仿真结果Fig.16 Simulation results of self-resonant grid-connected current before adding the suppression strategy
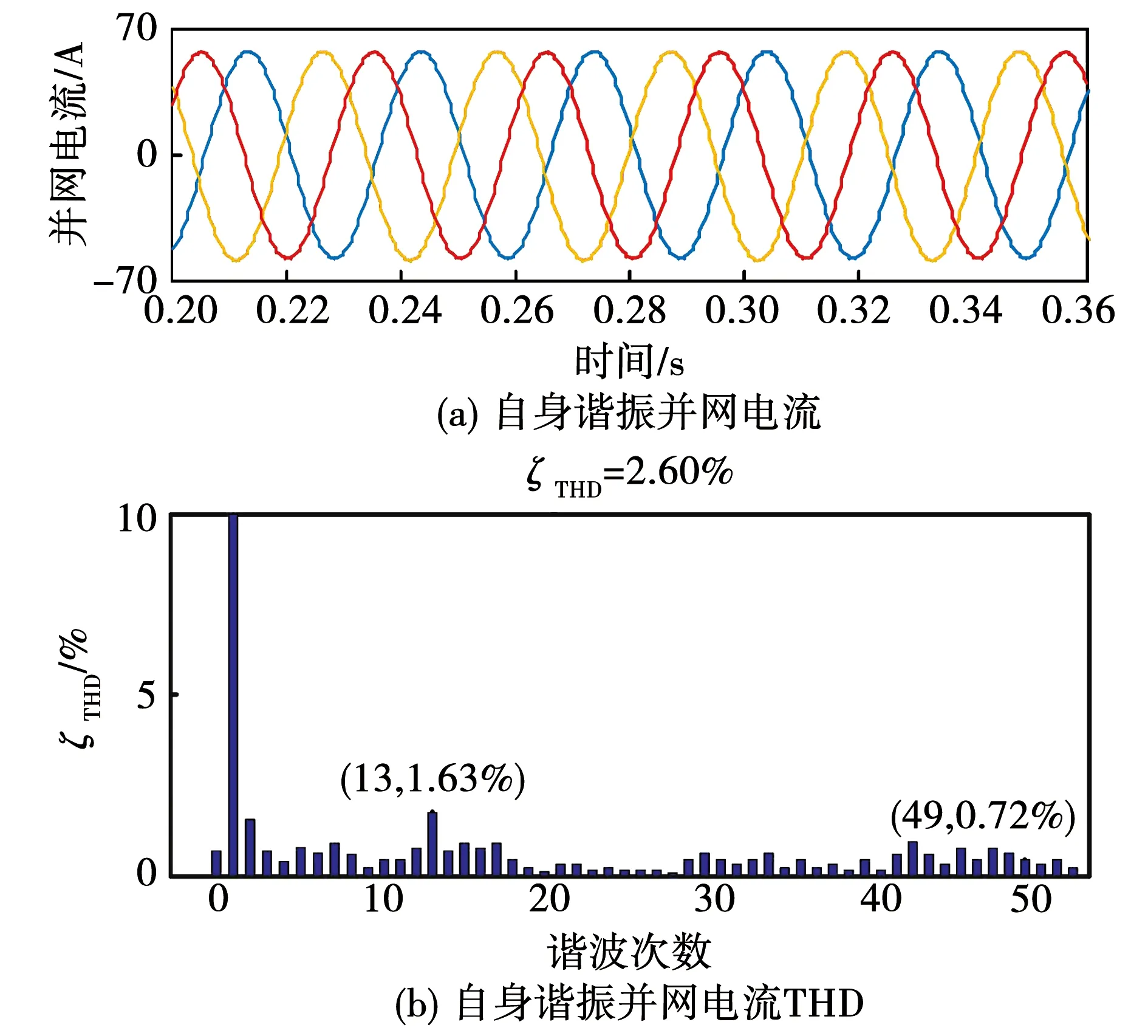
图17 加入抑制策略后自身谐振并网电流仿真结果Fig.17 Simulation results of self-resonant grid-connected current after adding suppression strategy
在未应用抑制策略前并联谐振电流仿真结果如图18(a)、18(b)所示。并联谐振同样会使并网电流发生畸变。经快速傅里叶变换分析后得出并网电流的畸变率为19.86%,其中低频段和高频段中依然存在突出的谐波放大现象,13次谐波含有率为6.40%,49次谐波含有率为18.15%,并联谐振导致的电流振荡会引发电能质量恶化,该仿真结果与图6并联谐振的幅频特性曲线结果一致。将添加抑制策略前后的并联谐振电流仿真结果图18(a)、18(b)和图19(a)、19(b)对比分析可知,应用该策略后电流振荡基本消除,总畸变率降为1.17%,13次和49次谐波分别降为0.88%和0.21%。符合图14分析结果。
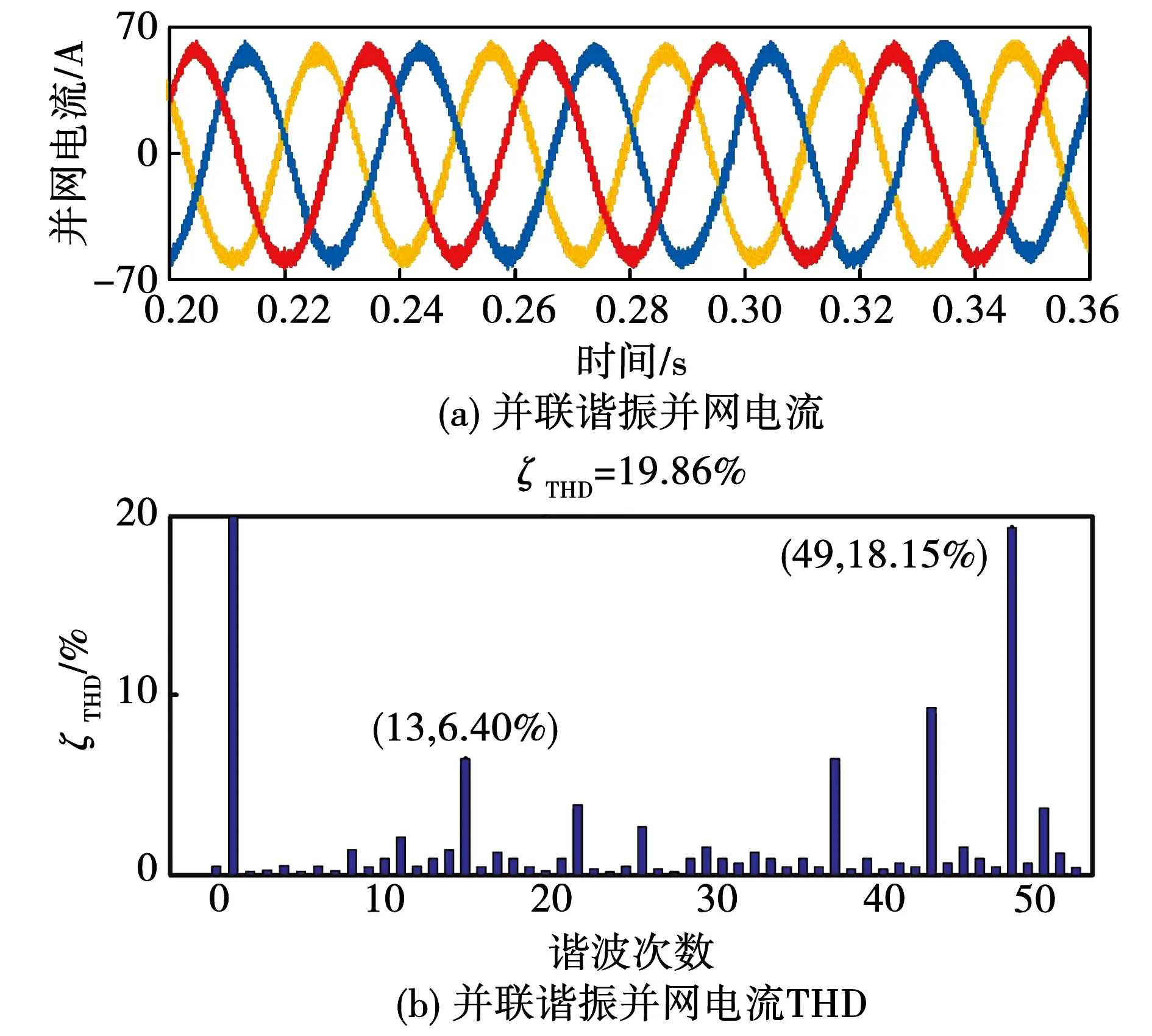
图18 加入抑制策略前自身谐振并网电流仿真结果Fig.18 Simulation results of self-resonant grid-connected current before adding suppression strategy

图20 加入抑制策略前串联谐振并网电流仿真结果Fig.20 Simulation results of series resonance grid-connected current before adding suppression strategy
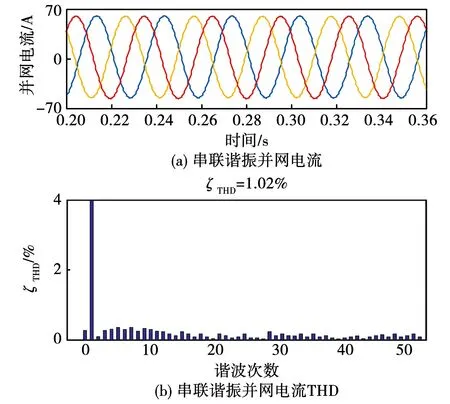
图21 加入抑制策略后串联谐振并网电流仿真结果Fig.21 Simulation results of series resonance grid-connected current after adding suppression strategy
串联谐振对并网电流的危害主要体现在低频段,当低频段的谐波放大时也会致使并网电流产生畸变,畸变率为8.82%。该仿真结果和图7的串联谐振伯德图分析结果相符。采用抑制策略后畸变率降为1.02%,低频处的稳定性得到改观,加强了系统鲁棒性,与图15添加抑制方法后的串联谐振幅频特性曲线分析结果相符。
4.2 不同容量并联逆变器并网运行
为验证该谐振抑制策略在不同容量逆变器并联条件下的有效性,选取额定容量为10 kW和20 kW逆变器各一台并联后并入电网。在t=0.36 s以前系统在不添加谐振抑制策略的情况下运行,在t=0.36 s时引入谐振抑制策略,直到仿真结束。
图22为引入抑制策略前后的并网电流波形图,据图可知t<0.36 s时,并网电流波形发生畸变,说明运行过程存在谐振。当t>0.36 s时,并网电流波形逐渐趋于平缓,经检测THD为0.63%,电能质量得到显著提高,并网电流谐振得到有效抑制。

图22 不同容量并联逆变器并网电流仿真结果Fig.22 Grid-connected current simulation results of parallel inverters with different capacities
4.3 系统鲁棒性分析验证
由上面验证结果可知,所提策略对谐振起到了良好的抑制作用,为进一步验证该策略对系统鲁棒性能的优化效果,仿真了逆变器投切过程中并网电流变化情况,此过程皆选用20 kW逆变器。首先进行单台逆变器运行到两台逆变器并联运行的工作方式转换。输出并网电流波形如图23所示,在0.10 s到0.18 s期间为单台逆变器运行,0.18 s时转换为两台逆变器并联运行。由图可知,并网电流只在切换时出现了轻微的振荡,并测得切换前后的电流THD分别为0.80%和0.93%,满足电流并网要求。

图23 单逆变器运行转换为两逆变器并联运行Fig.23 Conversion of single-inverter operation to two-inverter parallel operation
此外,进行了两逆变器并联运行到单台逆变器运行的工作方式转换,并网电流变化情况如图24所示,在0.38 s之前两台逆变器并联运行,0.38 s时断开其中一台逆变器。由图可知电流在投切前后电流均为平稳状态,各自THD分别为0.68%和0.77%,电流波形同样只在投切时略有波动。
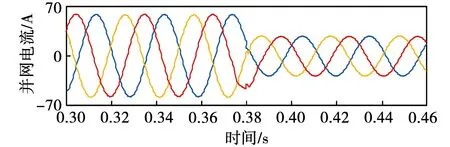
图24 两逆变器并联运行转换为单逆变器运行Fig.24 Conversion of two inverters in parallel operation to single inverter operation
以上仿真结果表明,在添加抑制策略后即使系统运行方式发生变化,并网电流仍能保持平稳入网,验证了引进谐振抑制策略后系统具有较强的鲁棒性。
5 实验验证
为进一步验证所提策略的实效性,本文基于光热与风能发电自治区重点实验室综合平台建立了2台20 kW逆变器并联实验,如图25为搭建的实验平台。实验中逆变器侧电感为1 mH,网侧电感为0.2 mH,滤波电容为20 μF,开关频率和采样频率分别取12 kHz和20 kHz。实验中提取了原系统的三相并网电流波形和加入抑制策略后的三相并网电流波形,所得结果如图26、图27所示。

图25 实验平台照片Fig.25 Experimental platform photos

图26 加入抑制策略前并网电流实验结果Fig.26 Grid-connected current test results before adding the suppression strategy

图27 加入抑制策略后并网电流实验结果Fig.27 Grid-connected current experiment results after adding suppression strategy
由图26可知,在未加入抑制策略前,并网电流产生畸变,电流波形有严重的振荡现象,说明的确有谐振存在,对系统稳定运行造成了干扰;加入抑制策略后的并网电流如图27所示,可以看出并网电流的畸变得到了显著抑制,振荡情况取得了有效的改善。实验结果与理论分析和仿真结果相符,说明该策略对谐振可以起到良好的抑制作用。
6 结 论
本文针对多逆变器并网谐振特性和抑制策略进行研究,得出以下结论:
1)通过串联虚拟电阻的方式可以增大系统阻尼,实现对谐振的直接抑制,弥补虚拟电容的局限性。考虑到系统的稳定性,需要对虚拟电阻定值进行计算,以5个逆变器并联而言,通过定值计算得到的电阻值为136 Ω时正好处于临界稳定值,在实现良好谐振抑制效果的同时也保证了系统的稳定性。
2)基于双闭环控制结构,引入虚拟电容算法可增强对高次谐波的滤除效果。对谐振发挥一定抑制作用,但该方法为间接抑制谐振,所以还有部分谐振存在,添加虚拟电阻以增加系统阻尼的方式对谐振起到直接抑制的作用。以准谐振控制器代替传统PI控制器具有较好的抑制环流效果,避免环流对谐振产生干扰。此外考虑到自谐振由欠阻尼三阶系统特性引起,因此引入电感电压反馈策略,电感电压反馈在有效降低系统阶次的同时摆脱了参数不稳定的约束。
3)为了获得具有一般意义的多并联逆变器谐振抑制结论,文章对相同容量和不同容量逆变器等多种组合进行仿真研究。通过逆变器投切仿真结果验证了系统具有较强鲁棒性。此外,进行两个20 kW逆变器并联实验,进一步说明了本文所提控制策略的有效性,此外可以改善系统鲁棒性能。

