考虑残余强度的层状岩体损伤演化规律
寇 昊 ,何 川 ,陈子全 ,周子寒 ,蒙 伟 ,肖龙鸽
(1.西南交通大学交通隧道工程教育部重点实验室,四川 成都 610031;2.中国建设基础设施有限公司,北京100029)
我国广泛分布着不同层理产状的岩体,如页岩、板岩、千枚岩等.由于其层理弱面的存在,导致不同倾角岩体力学性质之间的差异显著,这种岩性的各向异性对工程稳定与安全影响重大[1-2].
许多学者针对层状岩体的各向异性特征和损伤演化过程进行了理论与试验研究.刘运思等[3]采用内时理论并引入损伤变量,推导了层状岩体的内时损伤本构方程;史越等[4]建立了考虑单轴荷载损伤的层状千枚岩损伤本构模型,分析了不同层理角度下千枚岩的损伤演化特征;Wang 等[5]基于Drucker-Prager准则构建横观各向同性岩体的弹塑性本构模型;Saroglou 等[6]和Shi 等[7]分别采用各向异性指数kβ和αβ,修正Hoek-Brown 准则以描述层状岩体三轴强度的各向异性;Li 等[8]研究了横观各向同性板岩的尺寸效应;Pouragha 等[9]将砂岩、板岩看作黏结颗粒的集合体,结合局部强度准则和接触变形的微观力学公式,描述了层状岩体的强度各向异性特性;Gholami等[10]采用单轴、三轴和巴西劈裂试验评估了不同层理方向板岩的弹性参数和强度特性,具有明显U 形分布特征;衡帅等[11]、储超群等[12]分别研究了层状页岩和层状砂岩的力学行为、强度、破坏模式等的各向异性特性;邓华锋等[13-14]研究了层理弱面对砂岩的强度变形特征及纵波波速的影响机制;陈子全等[15]分析了千枚岩不同层理角度的能量损伤演化特征.上述研究多集中于层状岩体的力学参数、强度特性、破坏模式等,而对于其损伤演化的全过程研究尚不完善.
为了更好地描述岩石的应力-应变全过程变化曲线,刘冬桥等[16]基于花岗岩三轴压缩试验的缺陷发展过程,建立了应变软化损伤本构模型,反映出了岩石峰前和峰后的完整变形过程.温韬等[17]通过岩石损伤与耗散能的关系,建立了考虑岩石初始损伤和残余强度的本构模型.曹文贵等[18]将岩石承载看作由未损伤和损伤2 部分承担,提出了考虑残余强度的岩石损伤本构模型.李海潮等[19]从岩石损伤阈值角度,建立了反映低应力水平和残余强度变形特征的损伤模型.为更加真实准确地描述层状岩体的应变软化过程,本文基于横观各向同性材料的弹性本构方程,采用修正的Lemaitre 应变等价假设,推导了考虑残余强度的层状岩体损伤本构方程,通过页岩、千枚岩和板岩的三轴压缩试验数据验证了模型的合理性,最后分析了不同层理角度岩体的全过程损伤演化规律.
1 层状岩体损伤本构模型
1.1 层状岩体弹性本构方程
层状岩体往往存在明显的层理弱面,具有显著的强度各向异性,因此,可以将其视为横观各向同性材料[4],如图1 所示.图中:σx、σy、σz分别为x、y、z向的应力;θ为层理角度.在局部坐标系O1-x1y1z1中,横观各向同性材料的应力-应变关系为
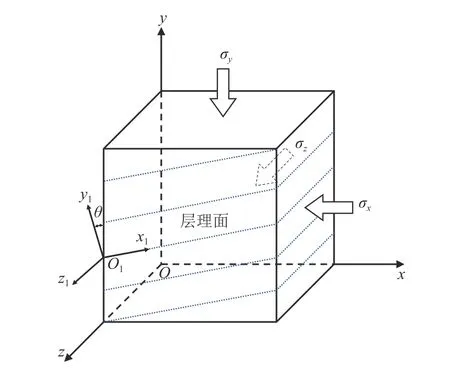
图1 横观各向同性材料坐标示意Fig.1 Diagram of coordinate system for the transversely isotropic materials
根据弹性力学局部坐标与整体坐标之间的转换关系,可得到整体坐标系O-xyz中,横观各向同性材料的应力-应变关系为
式中:
ε、σ、S分别为整体坐标系的应变张量、应力张量和柔度矩阵;A为坐标转换矩阵.
在三轴压缩条件下,切向应力为0,则应力(σx,σy,σz)与应变(εx,εy,εz)之间的关系为
1.2 考虑残余强度的层状岩体损伤本构方程
对于常规三轴压缩试验的圆柱体试件(图2),轴向应力σy=σ1,轴向应变为εy=ε1,围压σx=σz=σ3,则式(3)的第二式可以改写为

图2 圆柱体试件示意Fig.2 Schematic diagram of cylinder rock
岩体在外荷载作用下会产生损伤,许多学者采用Lemaitre 应变等价假设[20],引入损伤变量D进行损伤描述,可以得到
当岩体破坏时D=1,残余强度为0,往往与实际试验结果不符,不能体现出岩体破坏后的残余强度σr.因此,采用残余强度对Lemaitre 应变等价假设进行修正[19],得到
由于岩体内部损伤过程随机发生,具有随机分布的特征,因此,采用Weilbull 概率分布构建统计损伤本构模型[19-20],当荷载加载到应变ε1时,D可表示为
式中:m和ε0均为分布参数.
将式(8)代入式(7)得
考虑到岩体受荷达到峰值强度时(ε1=εc),其应力-应变应该满足以下2 个条件[19-20]:1)σ1=σc;2) ∂ σ1/∂ε1=0.其中,σc和εc分别为层状岩体应力-应变曲线在峰值强度处的应力值和应变值.
对式(9)求偏导可得
由条件 1) 可得
由条件 2)可得
联立式(11)和式(12)得到损伤本构模型的分布参数为
以E= 46.64 GPa,μ= 0.342,εc= 0.004 22,σc=147.29 MPa,σ3=10 MPa 的岩石为例,在考虑残余强度σr=83.4 MPa 时,m=3.291,ε0=0.00513;σr=0 时,m=3.6976,ε0=0.00597.上述2 种情况的应力-应变曲线和损伤过程曲线如图3 所示.可以看出,考虑残余强度所得到的应力-应变关系曲线更加真实;此外,考虑残余强度的岩石在加载过程中的损伤和损伤速率均提前,且考虑残余强度的最大损伤速率增大,2 种情况的损伤演化过程存在明显的差异.可见,采用考虑残余强度的损伤本构模型进行损伤演化规律研究才更加合理.

图3 考虑残余强度与不考虑残余强度对比Fig.3 Comparison between the considered and unconsidered residual strengths
2 模型验证
为了验证上一节层状岩体损伤本构模型的准确性,以贾长贵等[21-23]的层状页岩、千枚岩、板岩三轴压缩试验结果进行检验.将贾长贵等[21]在不同围压条件下考虑层理角度分别为0°、30°、60°、90° 的页岩压缩试验结果代入式(13)、(14),可以得到该页岩损伤本构模型的m和ε0,如表1 所示.根据唐克东等[22-23]的千枚岩、板岩三轴压缩试验结果,得到损伤本构模型参数如表2 所示,受篇幅限制,仅列出围压为10 MPa 的主要参数.

表1 页岩三轴压缩试验的主要参数[21]Tab.1 Main parameters of triaxial compression test for shale [21]

表2 千枚岩、板岩三轴压缩试验的主要参数[22-23] (σ3=10 MPa)Tab.2 Main parameters of triaxial compression test for phyllite and slate [22-23] (σ3 = 10 MPa)
由式(4)中的Eθ可以计算得到弹性模量的理论值,其中,由试验得到的页岩μ、μ1分别为0.37 和0.34,千枚岩μ、μ1分别为0.30 和0.28,板岩μ、μ1均为0.20,G1可由任意层理角度的试验值计算,即
弹性模量理论值与试验值的对比如图4 所示.由图可知:不同层理角度的弹性模量理论值与试验值较为接近,层理角度小于45° 时弹性模量基本不变,大于45° 后表现为随着层理角度的增加而增大;当θ=0° 时,岩体整体刚度由层理弱面控制,压缩变形相对较大,弹性模量小;当θ=90° 时,岩体整体刚度则由基质起主导作用,抵抗变形能力增强,因而弹性模量变大[12].可见该理论解能够反映层状岩体弹性模量受层理角度的影响.

图4 弹性模量的理论值与试验值对比Fig.4 Comparison between theoretical and experimental values of elastic modulus
通过考虑残余强度的层状岩体损伤本构模型得到不同层理角度的页岩、千枚岩和板岩三轴压缩应力-应变关系理论值,将其与试验值进行对比(图5和图6),可见理论计算的应力-应变关系曲线与试验曲线形态基本一致,可以很好地描述岩体的弹性变形阶段,还可以较好地体现出岩体峰后的应变软化过程,整体上能够反映层状岩体的力学行为.

图5 页岩应力-应变关系的理论值与试验值对比Fig.5 Comparison between theoretical and experimental values of stress-strain curves for shale

图6 千枚岩、板岩应力-应变关系的理论值与试验值对比Fig.6 Comparison between theoretical and experimental values of stress-strain curves for phyllite and slate
3 层状岩体损伤演化规律研究
根据表1 和表2 的试验参数,由式(8)计算可得层状页岩、千枚岩和板岩的损伤变量D在整个加载过程中的变化规律,如图7 和图8 所示.不同于文献[4, 20],由于其未考虑残余强度,损伤演化曲线整体向右发生偏移,与实际对应的应力-应变曲线有所偏差.本文的损伤演化曲线更符合试验结果,整体表现为:在前期加载过程中岩体处于压密阶段,损伤基本为0 (未发生损伤);随着应力的增加,岩体内部裂隙开始萌生、发展,直至贯通破坏,损伤也相应呈现出缓慢增长、加速增长、减速增长以及达到残余强度后稳定于1.

图7 页岩的损伤演化曲线Fig.7 Damage evolution curves of shale
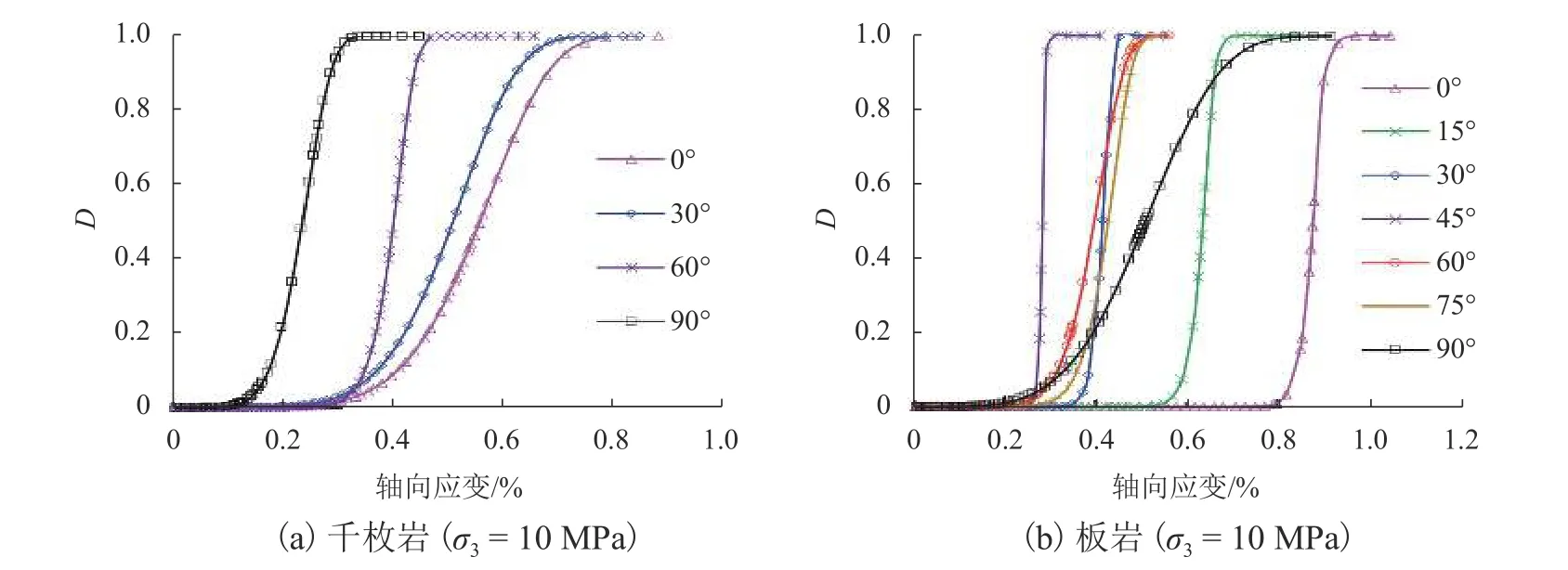
图8 千枚岩、板岩的损伤演化曲线Fig.8 Damage evolution curves of phyllite and slate
从图7 还可以清晰看到,页岩层理角度为60°的岩体损伤演化曲线最陡,损伤发展速度最快,最先破坏;对比相同围压(10 MPa)的页岩、千枚岩和板岩损伤演化曲线,千枚岩相较页岩、板岩的层厚更薄,强度更低,层理角度为90° 时最先破坏,而板岩相对较厚,强度更高,层理角度为45° 时最先破坏.在单轴压缩条件下,层理角度为60° 的页岩最先发生损伤;在三轴压缩条件下,层理角度为90° 的页岩最先发生损伤,并且围压越大,损伤开始位置越靠前.在10 MPa 围压作用下的千枚岩、板岩也是层理角度为90° 时最先发生损伤.当岩体层理角度为90° 时,单轴压缩下岩体发生劈裂张拉破坏,三轴压缩下岩体发生张剪破坏[13].由于围压的作用约束了环向变形,因而偏应力作用下使得作为岩体主要刚度贡献者的基质首先发生损伤,但损伤增速小于层理角度为45°/60° 的岩体.当层理角度为0° 时,不论单轴还是三轴压缩,岩体的变形均由层理弱面控制,总体表现为穿越基质和层理面的张剪破坏[14],损伤相对滞后.
从上述层状岩体损伤演化过程分析可以看出,由于岩体层理弱面的存在,导致其力学性能和破坏模式的各向异性,损伤演化规律也表现出了显著的差异性.
4 结 论
1) 建立了考虑残余强度的层状岩体损伤本构模型,采用层状页岩、千枚岩和板岩的三轴试验数据对模型进行了验证.该模型不仅能够很好地描述层状岩体的弹性变形阶段,还可以较好地体现出岩体峰后的应变软化过程,整体上能够反映层状岩体的力学行为.
2) 该模型得到的损伤演化曲线更加符合实际.初期加载过程中损伤基本为0 (未发生损伤),随着应力的增加,损伤值呈现出缓慢增长、加速增长、减速增长以及达到残余强度后稳定于1.
3) 页岩层理角度为60° 时,损伤演化曲线最陡,损伤发展速度最快,最先破坏;千枚岩相较页岩、板岩的层厚更薄,强度更低,层理角度为90° 时最先破坏,而板岩相对较厚,强度更高,层理角度为45° 时最先破坏.
4) 三轴压缩条件下,围压越大,层理角度为90° 的岩体损伤起始位置越靠前,表明围压的作用使得其主要刚度贡献的基质体损伤提前.层理角度为0° 的岩体损伤位置相对靠后,表明层理弱面提供了变形使得损伤滞后.

