LUCIFER 算法置换表的量子可逆线路实现

陈 华，傅美容

（1.中国电子学会办公室，北京 100036；2.北京联合大学特殊教育学院特殊教育系，北京 100101）

1 研究背景

如果数字组合逻辑电路将每个输入模式映射到唯一的输出模式，则称该电路为可逆电路［1］。根据Landauer［2］的证明，不管底层技术如何实现，如果使用传统的不可逆逻辑门必定会产生功耗。而根据Bennett［3］的结果，假使为了让功率不在任意的电路中被消耗，则电路必须由可逆门组成。由此，可逆电路在低功耗CMOS 设计［4］、光学计算［5］、量子计算［6］和纳米技术［7］中广受关注。

与传统的不可逆电路的不同之外在于，可逆电路要求输入、输出之间存在双射，并且电路中不能有扇入、扇出及反馈的存在，使可逆电路研究比不可逆电路研究更加复杂，到目前为止并没有通用且高效的算法。对于任意大小的可逆函数，寻找其最优电路通常很困难，因此出现了一些启发式的方法来求解，其中包含基于环理论、转换、二元决策图、搜索的方法等［8］。LUCIFER算法是DES算法的前身，其置换表为四元可逆函数。本文基于环理论方法中的相关知识，并结合文献［1］中介绍的构造方法开展该算法置换表的量子可逆电路实现研究。

全文安排如下：第2 节介绍相关基本概念及实现方法，第3节中讨论LUCIFER 算法置换表量子电路实现的详细步骤，讨论部分放在第4节。

2 方法介绍

本节中，我们主要介绍实现量子线路的主要方法及相关基本知识。

2.1 CmNOT 门

一种量子门能实现一种可逆函数。广义Toffoli门CmNOT(x1，x2，…，xm+1)表示前m比特为控制线，当且仅当每一条控制线值都为1 时，才使得目标线xm+1的结果翻转，即x1=x1，…，xm=xm，xm+1=xm+1⊕x1*x2*…*xm。构成通用门集合的NOT门、CNOT门、Toffoli门也可以写成C0NOT，C1NOT，C2NOT。

2.2 置换群

设Ω是由n个文字组成的集合：

Ω到自身的一个映射称为（作用于）Ω上的一个置换，或n元置换，简称置换。

一般地，如果n元置换σ把n个文字中的一部分α1，α2，…，αm(m≤n) 作 如 下 变 换 ：ασ1=α2，ασ2=α3，…，ασm=α1，而其余n-m个文字保持不变，则称σ为一个m轮换，简称轮换，记作σ={α1，α2，…，αm}。m称为轮换的长度。m=1 时，σ就是恒等置换。当m=2时，称为一个对换［9］。

定理1任何一个置换都可以表示成一些不相交的轮换的乘积，而且表示法（除轮换的次序外）是唯一的［9］。

定理2每个n元置换均能表示成若干个对换的乘积，如

很明显，若两个轮换之间没有公共元素，则称它们相互独立，相互独立的轮换之间满足乘法交换律［9］。

2.3 方法步骤

下面我们将简要描述文献［1］中的方法，即如何在不额外添加辅助量子比特的情况下，通过NOT门和CmNOT门来构造量子电路。

定义1如果两个n维向量u，s只有1 比特不同，就称置换(u，s)为一个相邻对换。

引理1假设u，s中有且只有1 比特Bj不同，l个比特相同且都为0，分别为Bi1，…，Bil。则有(u，s) =Ni1*…*Nil*Cj*Ni1*…*Nil。其中Ni表示第i比特上为NOT门，Cj表示第j比特为目标位，其余比特为控制位。

注意：NOT 门的乘积存在交换性，同一量子线路中的相邻一对NOT门可以去掉。

引理2如果两个n维向量u，s有k个比特不同，则 存 在 一 个 有 序 集 合M={d1，d2，…，dk+1}，d1=u，dk+1=s，并且对于任意的i，1 ≤i≤k+1，di和di+1之间只存在1 比特差异，有（u，s）=（d1，d2）（d2，d3）…（dk，dk+1）（dk，dk-1）…（d2，d1）。

算法步骤：

规则一：检查函数f的真值表。考虑一个给定的可逆线路的真值表，每个输出比特有2n个值，将它们与输入比特一一对比，如果相异数大于2n-1，则需在这个比特的线路上添加NOT门。

规则二：以一系列对换乘积的形式将可逆线路进行分解，保证最终形式中的每一个对换之间相异比特数为1。

规则三：根据引理1，将每个对换分解成NOT门和CmNOT门。

2.4 算法可行性

一个n量子比特的可逆线路是对称群S2n中的一个置换，反之亦然。两个门的级联等价于S2n中两个置换相乘。根据定理2 可知，任何置换群都可以用一系列的对换相乘，通过引理1，可证明一个置换可以表示成一系列量子门的级联形式。同样地，根据文献［1］中给出的证明及结论，该构造方法对于任意的n量子比特可逆函数都适用，且量子线路中至多出现2n·N个CmNOT 门和4n2·N个NOT 门，N表示输出与输出对应不同的个数。

3 实现过程

在20 世纪60 年代后期，IBM 公司成立了一个由Horst Feistel负责的计算机密码学研究项目，1971年设计了分组密码算法LUCIFER，该算法分组长度为64、密钥长度为128 位。它就是DES 算法的前身，该算法的一个置换真值表如表1所示。

表1 置换真值表

根据真值表，可以写出置换群表示为

第一步：将B列与P列一一对比后可知，相异数分别为（10 8 8 12），依据算法规则一，则需要在第一条和第四条添加NOT门。

第二步：添加NOT 门之后的真值表如表2 所示。根据新的真值表，可以写出置换群表示为

表2 添加NOT 门之后的置换真值表

第三步：根据定理2，可将f分解成如下对换乘积形式为

第四步：根据引理1 和引理2，写出所有对换的表达式，即

经过合并简化，最终置换表分解成为54个NOT门和35个CmNOT门。电路图表示如图1所示。

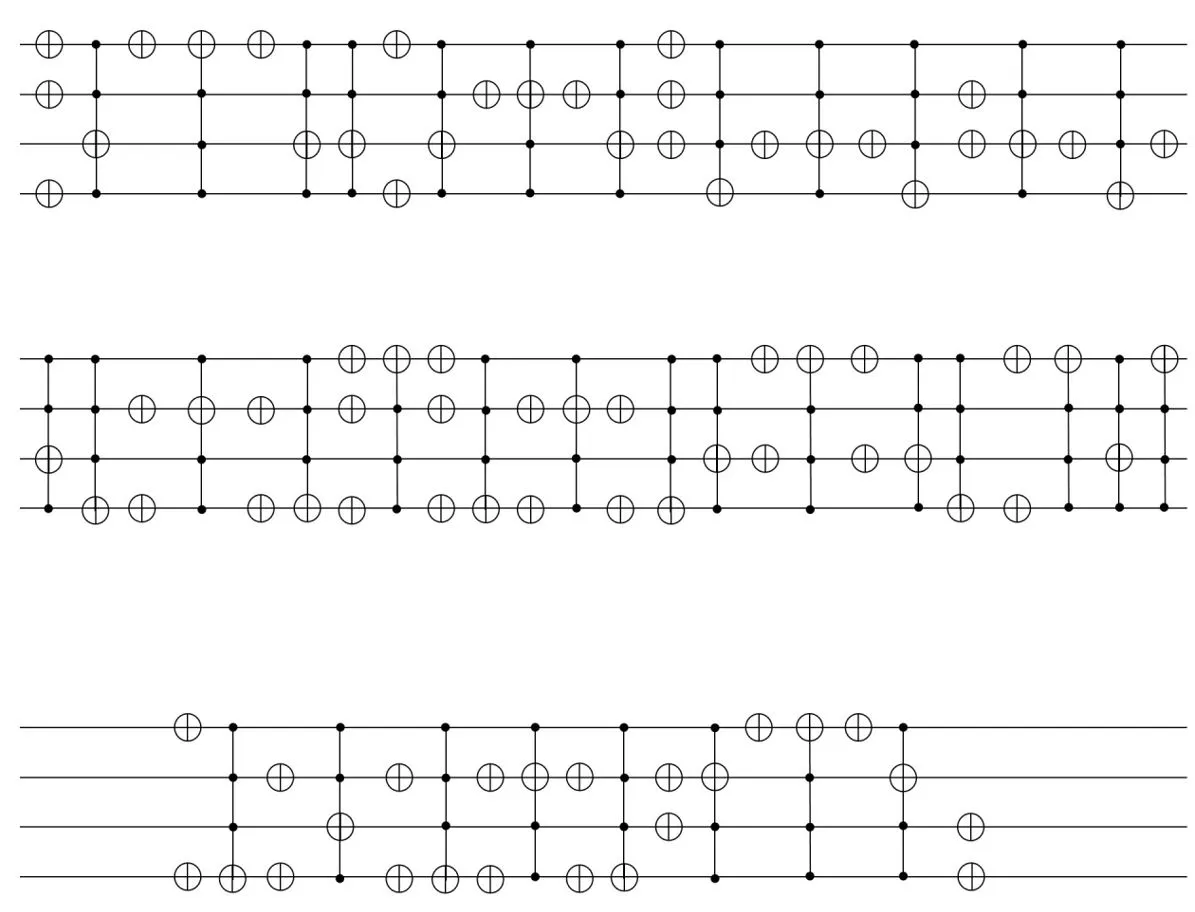
图1 LUCIFER 算法置换真值表的量子可逆线路图

4 讨论

本文以LUCIFER算法置换表为重点，介绍了量子门及置换群中的相关理论，详细列举实现其量子可逆线路的方法及步骤，并给出线路示意图，使读者对LUCIFER 算法的结构有了更深刻的认识。面对更高维度的置换表，其量子线路的复杂度如何，以及有无更高效的线路实现方法等，还需要进一步开展研究。