秩为1方阵的特征向量的一种新求法
阚永志
秩为1方阵的特征向量的一种新求法
阚永志
(辽宁工业大学 理学院,辽宁 锦州 121001)
利用“秩为1的方阵可表示为一非零列向量与非零行向量的乘积”的结论及特征值和特征向量的定义,建立秩为1方阵的二次多项式,利用分块矩阵的乘积,给出非零特征值所对应的特征向量的一种新求解方法及计算公式,利用齐次线性方程组的基础解系求解方法给出零特征值所对应的特征向量的计算公式。提出的新求解方法可以有效地减少计算量,同时可以直接地写出所求解方阵的特征向量。
秩;方阵;基础解系;特征值;特征向量
特征值与特征向量在许多领域有着非常广泛的应用,如工程技术中的振动问题和稳定性问题[1],常可归结为求一个方阵的特征值和特征向量的问题;方阵的相似对角化问题[2-5]和信号处理、数据挖掘等学科[6]及微分方程组的求解[7-10]就要用到特征值和特征向量的理论。由于秩为1的方阵自身有其独特的性质和应用[11-14],因此,对其特征向量的求解问题进行研究是必要的。但传统求解方法[1]的求解计算过程繁琐以及难以理解,且只能按照求解齐次线性方程组非零解的步骤进行,为此,本文给出了秩为1方阵的特征向量的一种新的更为简单的求解方法。
1 预备知识
引理1[1]()=1的充分必要条件是存在非零列向量及非零行向量T,使=T。
证明 先证充分性。
设非零列向量=(1,2,…,a)T,=(1,2,…,b)T,并不妨设11≠0。根据矩阵秩的基本性质(()≤min{(),()})及=T,有()≤()=1;另一方面,的第(1,1)元11≠0,知()≥1,于是()=1。
再证必要性。
设=(a)×,()=1,并不妨设a≠0。因()=1,根据矩阵秩的定义,知的所有二阶子式均为零,故对的任一元a(≠,≠),有
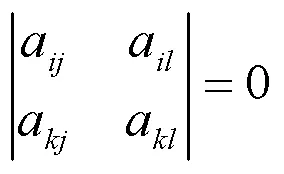
即aa=aa。显然,当=或=时,上式也成立。于是
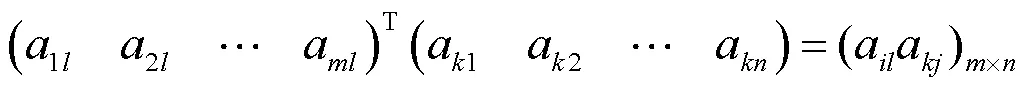
即(aa)×=aA。因a≠0,所以
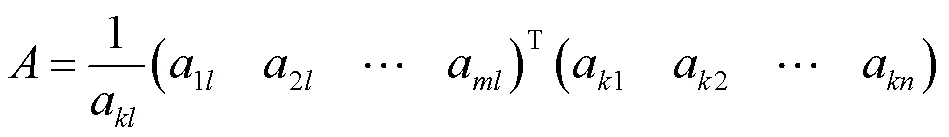
令
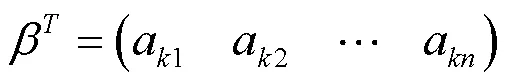
故、T分别是非零列向量和非零行向量,且有=T。

2 主要结果及其证明
设阶方阵=(a)的秩为1,根据引理1,不妨记=T,其中、均为非零列向量;根据引理2,的个特征值如式(1)所示。
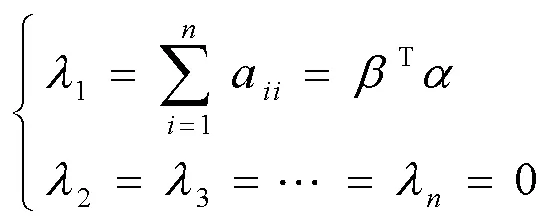
这说明,若方阵的秩为1,那么在求特征值时,可直接利用引理2写出其特征值。
本文给出以下定理及其证明。
定理 若阶方阵=(a)可表示为=(1,2,…, x)T(1,2,…, y),x,y(=1,2,…,)都不同时为0,则的对应于特征值
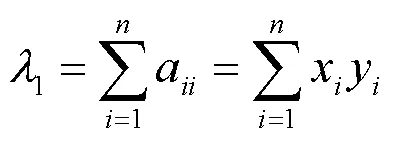
的全部特征向量为1(1≠0),其中=(1,2,…, x)T;的对应于特征值2=3=…=λ=0的全部特征向量为22+33+…+cξ(2,3,…, c不同时为0),2=(−2,1, 0,…, 0)T,3=(−3, 0,1,…, 0)T,…,ξ=(−y, 0, 0,…,1)T。
证明 先求的对应于特征值1的特征向量。
设=T=(1,2,…, x)T(1,2,…, y),其中=(1,2,…, x)T,=(1,2,…, y),则

再令=(1,2,…, a),则由2=1,得(1,2,…, a)=1(1,2,…, a),Aa=1a(=1, 2,…,),其中a=(1y,2y,…,xy)T,可知即为的对应于特征值1的一个线性无关的特征向量,故的对应于特征值1的全部特征向量为1(1≠0)。
再求的对应于特征值2=3=…=λ=0的特征向量。
由
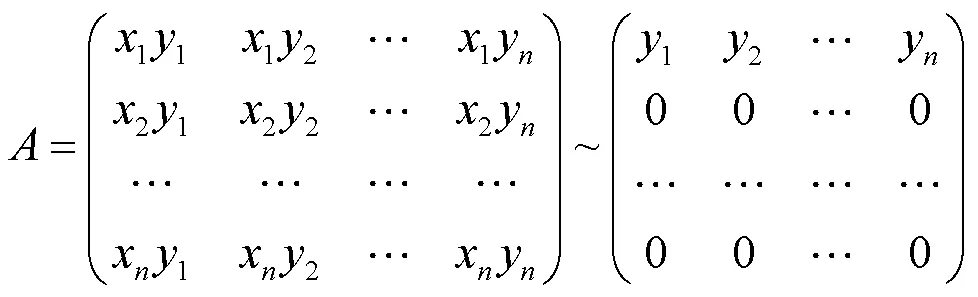
知=0的基础解系可取为2=(−2,1, 0,…, 0)T,3=(−3, 0,1,…, 0)T,…,ξ=(−y, 0, 0,…,1)T。从而,的对应于特征值2=3=…=λ=0的全部特征向量是22+33+…+cξ(2,3,…, c不同时为0)。
根据上述定理,即可直接写出秩为1方阵对应于非零特征值和零特征值的特征向量。
3 应用实例
本文只以秩为1的方阵为例说明。
例 求矩阵的特征值和特征向量。

(1)传统的求解方法
先求的特征值。由
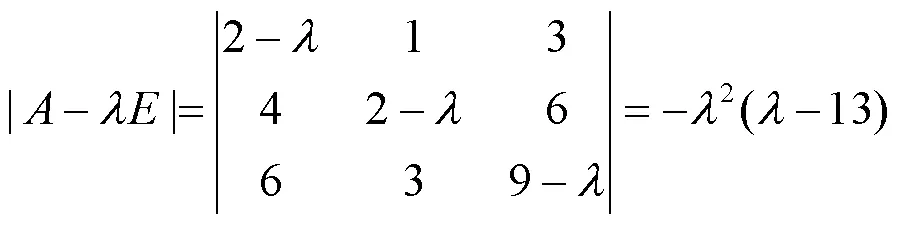
求得的特征值为1=13,2=3=0。
下面再求各特征值所对应的特征向量。
当1=13时,解(-13)=0。
由
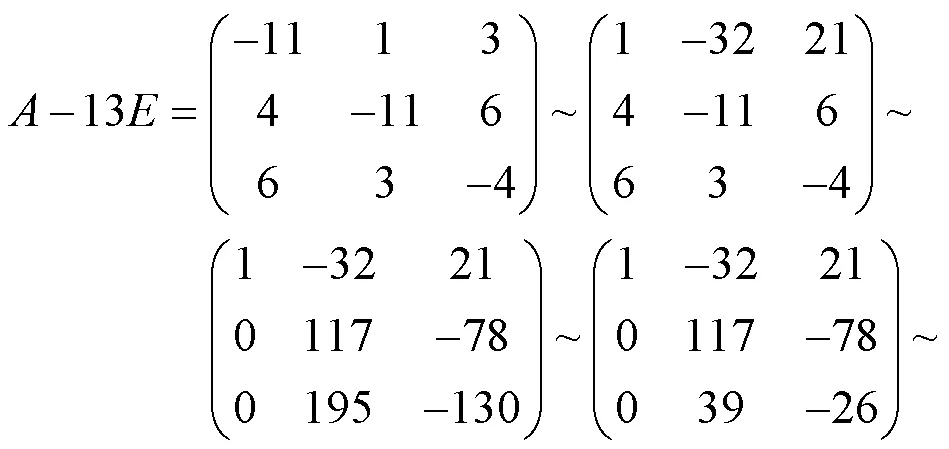
得等价方程组
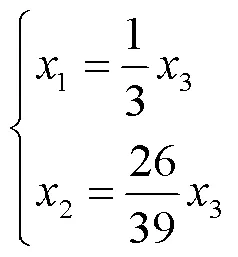
取基础解系1=(1/3, 26/39, 1)T,所以的对应于特征值1=13的全部特征向量为11,(1≠0)。
当2=3=0时,解=0。
由
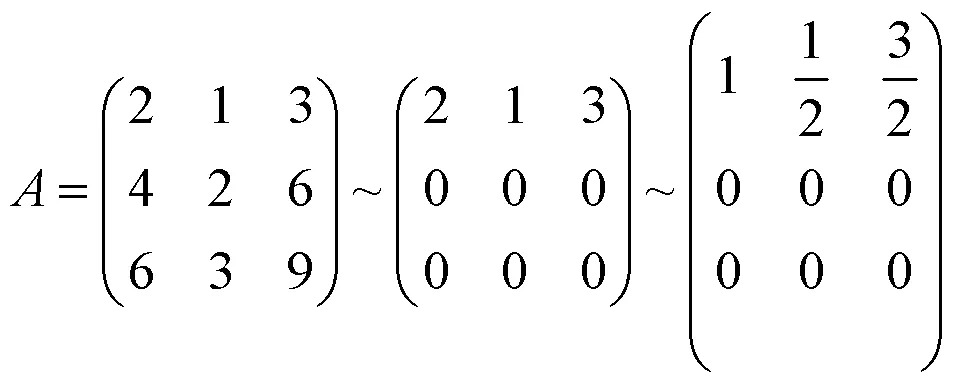
得等价方程组:
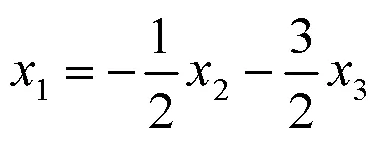
取基础解系2=(−1/2, 1, 0)T,3=(−3/2, 0, 1)T,所以的对应于特征值2=3=0的全部特征向量为22+33,(2、3不同时为0)。
(2)新的简便求解方法
不妨令=T,其中(1, 2, 3)T,=(2, 1, 3)T,则根据上述定理,知的对应于特征值1=T=13的全部特征向量为1(1≠0)。
的对应于特征值2=3=0的全部特征向量为:2(−2,1, 0)T+3(−3, 0,1)T=2(−1, 2, 0)T+3(−3, 0, 2)T,(2、3不同时为0)。
4 结束语
本文针对秩为1方阵的特征值和特征向量的研究,利用分块矩阵的乘法及特征值和特征向量的定义,找到一种新的求解方法。通过实例解法对比,本文新的求解方法显然要比传统解法更为简单,本文的研究结果具有了一定的创新和参考价值及实用价值。
[1] 同济大学数学系. 工程数学线性代数[M]. 北京: 高等教育出版社, 2007.
[2] 白昊月. 方阵可对角化的应用研究[J]. 黑龙江科学, 2022, 13(13): 144-146.
[3] 蒋启芬. 对称与非对称实方阵相似对角化问题的注记[J].高等数学研究, 2021, 24(6): 76-78.
[4] 刘国华, 许杨. 从特征值到特征向量以及相关应用[J]. 大学数学, 2021, 37(3): 9-12.
[5] 戢伟. 实对称矩阵正交相似对角化的教学研究[J]. 高师理科学刊, 2019, 39(5): 60-63.
[6] 王玉鹏, 晋民杰. 浅谈特征值与特征向量教学方法[J]. 教育现代化, 2019, 6(67): 157-158.
[7] 崇金凤, 卓泽朋. 方阵的特征值和特征向量[J]. 洛阳师范学院学报, 2015, 34(11): 24-26.
[8] 刘素兵, 曲娜, 曹大志. 关于方阵的特征值与特征向量教学的探讨[J]. 高师理科学刊, 2017, 37(10): 62-65.
[9] 卞小霞. 关于特征值及特征向量的教学分析[J]. 林区教学, 2017(11): 68-70.
[10] 林大华, 戴立辉. 矩阵特征值在矩阵中的作用[J]. 赤峰学院学报: 自然科学版, 2017, 33(10): 8-9.
[11] 余建熙. 秩为1矩阵的性质及应用[J]. 当代教育实践与科学研究, 2017(10): 260-261.
[12] 吴马威, 陈益智. 秩为1方阵的几个性质及应用[J]. 纺织高校基础科学学报, 2015, 28(1): 4-8.
[13] 邵逸民. 秩为1矩阵的性质及应用[J]. 大学数学, 2010(26): 194-197.
[14] 杨桂元. 秩等于1矩阵的有关性质[J]. 大学数学, 2006(22): 127-128.
[15] 阚永志, 周绍华. 谈秩为1的方阵的特征值的求法[J]. 辽宁工学院学报: 自然科学版, 2005, 25(4): 278-280.
A New Method for Finding the Eigenvector to a Square Matrix of Rank 1
KAN Yong-zhi
(College of Science, Liaoning University of Technology, Jinzhou 121001, China)
Based on the conclusion that a square matrix of rank 1 can be represented as a product of a non-zero column vector and a non-zero row vector and the definition of eigenvalues and eigenvectors, a quadratic polynomial of rank 1 square matrix is established, and a new solution method and calculation formula of eigenvectors corresponding to non-zero eigenvalues are given by using the product of block matrices. The formula for calculating the eigenvector corresponding to zero eigenvalue is given by using the system of homogeneous linear equations. The proposed new solution method can effectively reduce the amount of calculation, and at the same time, the eigenvectors of the square matrix can be written directly.
rank; square matrix; basis system of solutions; eigenvalue; eigenvector
10.15916/j.issn1674-3261.2023.05.013
O29
A
1674-3261(2023)05-0348-03
2023-06-02
阚永志(1970-),男,辽宁义县人,副教授,硕士。
责任编辑:陈 明

