带有治疗函数与双线性接触率的SIRS传染病模型的全局分析
周美涛
带有治疗函数与双线性接触率的SIRS传染病模型的全局分析
周美涛
(辽宁工业大学 理学院,辽宁 锦州 121001)
对带有治疗函数与双线性接触率的SIRS传染病模型的全局动力学进行了分析,通过数学分析得到系统不存在极限环的充分性判据。当系统不存在极限环时,通过治疗和控制就能够消除传染病,此时传染病不会成为地方性流行病;当系统存在极限环时,则这是一个不稳定的极限环,即亚临界Hopf分支,此时通过治疗仍能消除传染病。
传染病;极限环;全局分析
传染病长期威胁着人们的生命和财产安全,传染病的传播备受大家的关注。国内外多名学者应用动力学理论通过建立数学模型研究传染病的传播动力学和渐进行为[1-11]。动力学方法[2]是通过讨论传染病的传播机理来探索传染病的传播规律,从而能够更好的了解传染病扩散。在研究传染病所使用的模型中,选择一个合适的治疗函数是非常关键的,文献[5]建立的SIR传染病模型中使用了治疗函数,使用这个治疗函数表明随着感染者数量的增加,逐渐增大治疗能力,当感染者数量饱和时,对疾病采取最大限度的治疗,从而能够使传染病尽快得到控制,该治疗函数如式(1)所示。

式中:表示疾病的治疗率;表示感染者数量;0表示感染者数量达到饱和时的临界值;=0表示疾病的最大治疗能力。
对于传染病来说,由于其非常危险并且蔓延非常迅速,蔓延一段时间后会造成医疗机构的治疗能力不足,为了能够在短时间内控制传染病的传播,此时可以采用最大的治疗能力来治疗传染病,以便能在最短的时间内控制疾病的传播。通过对传染病的研究发现,在日常生活中很多传染病的患者不具有终身免疫力,只具有临时免疫力[6-9],在感染者康复一段时间后可能会再次感染。基于这个原因,本文采用双线性发生率和最大治疗能力()=作为治疗函数来建立SIRS传染病模型,如式(2)所示。
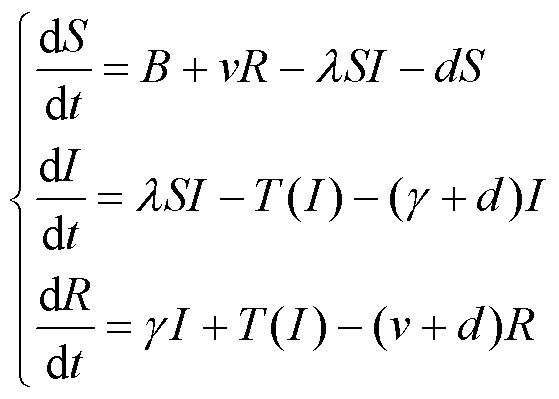
式中:表示时刻的易感者数量;表示时刻的感染者数量;表示时刻获得临时免疫的康复者数量;表示总人口对时间的输入率;表示人口的自然死亡率;表示双线性发生率;表示感染者的自然恢复率;表示患者的临时免疫力;假设所有符号均为正数。
在文献[6]中讨论了SIRS传染病模型平衡点的存在性和稳定性,并对所得结论进行了数值模拟。本文中将式(2)所示的模型及其简化形式称之为系统,并对系统(2)的全局动力学结构进行讨论,如果系统(2)不存在极限环,那么系统(2)具有简单的动力学行为。下面结合文献[6]对系统(2)的全局结构进行分析,解决系统(2)是否存在极限环的问题。
1 极限环分析
首先将系统(2)进行简化处理,将系统(2)的3个方程相加,记时刻的人口数为,这里=++,经计算可得式(3)。
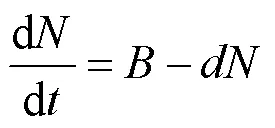
由(3)式可知,当→∞时趋向于常数[9],所以在平面++=0上,可简化系统(2)如式(4)所示。
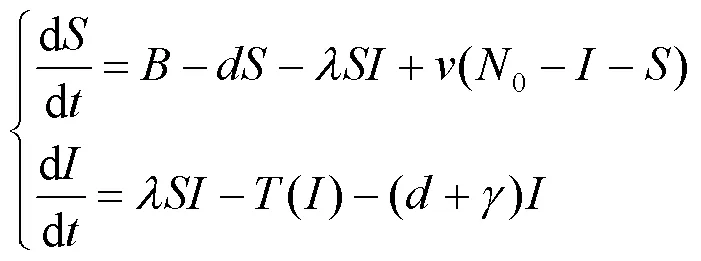
下面对系统(4)平衡点的全局结构进行讨论,为了方便叙述定义式(5)与式(6)2个等式。



由文献[6]的定理2可知:如果系统(4)存在地方病平衡点1,则1一定是个鞍点,所以在地方病平衡点1附近不会产生极限环;如果地方病平衡点2存在,则平衡点2可能是焦点,可能是结点,也可能是中心,并且随着参数值的改变平衡点2的稳定性也会发生变化,所以在平衡点2附近可能会存在极限环。如果系统(4)的平衡点2附近没有极限环,则系统(4)的动力学行为比较简单,有利于分析传染病的发展。

首先令=-2,=-2,则系统(4)变为(8)。

然后令=-(+)-(++),=+,则系统(8)变为(9)。
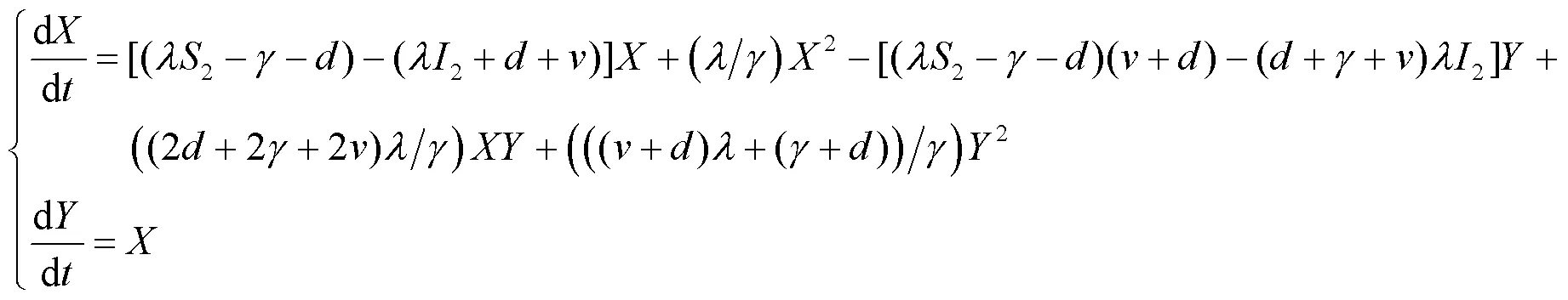
经计算可得式(10)。
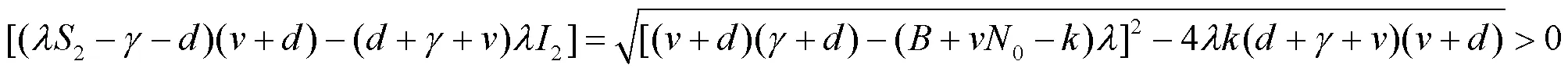
最后令
则系统(9)变为(11)。

经过上面的讨论可以得到定理1。
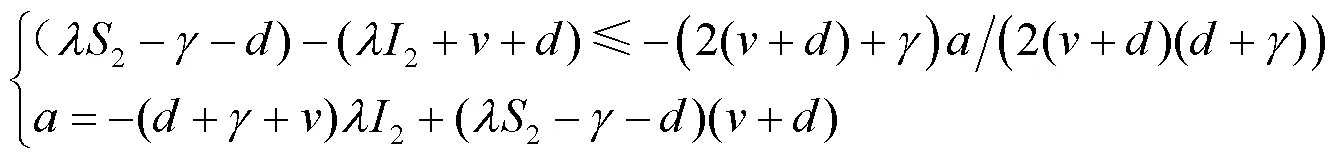
则系统(2)不存在极限环。
证明 当定理1的条件成立时,为了证明系统(2)不存在极限环,对系统(11)做变量替换。令=,=,计算可得:

由文献[6]中定理3的证明可知:
因此,
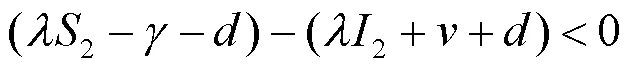
所以<0。
因为/>0,/>0,由参考文献[9]中引理12.1可知+/2≤0成立时,系统(2)不存在极限环。
由、、的定义可知+/2≤0等价于:
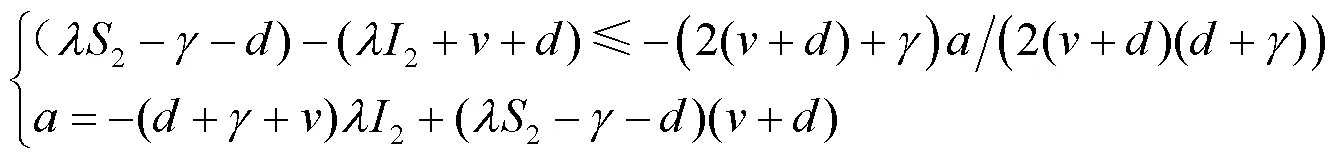
所以如果定理1的条件成立,则系统(2)不存在极限环,即定理1的结论得证。

则系统(2)不存在极限环。
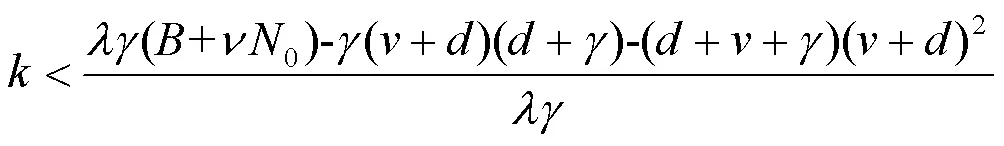
证明 当系统(2)的简化系统(4)存在平衡点2时,记2为系统(4)在平衡点2处的Jacobian矩阵:
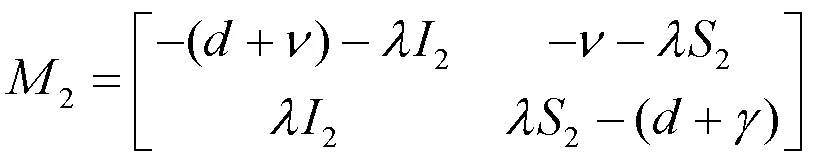
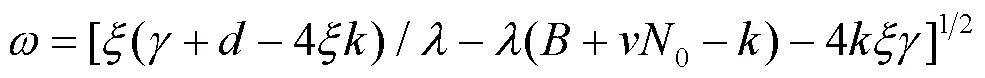
此时tr(2)对求导可得
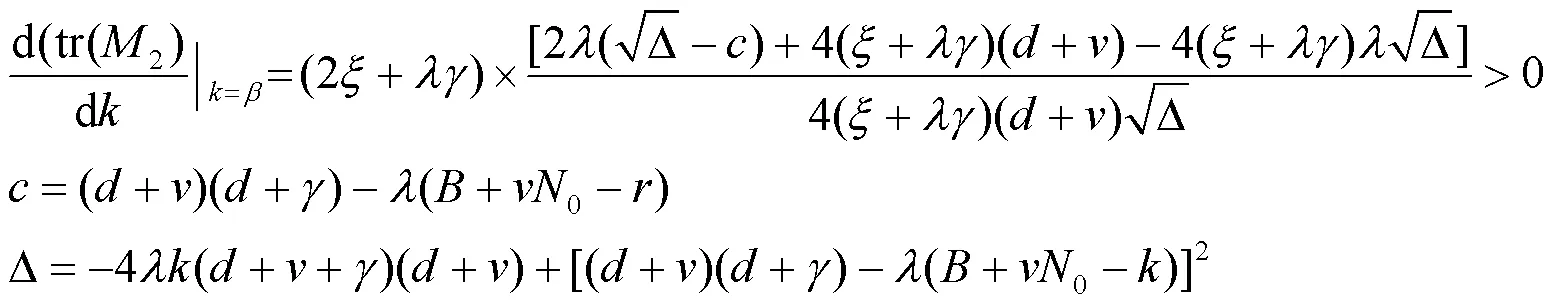
根据文献[10]中定理3.4.2可知=为系统(4)的Hopf分支点。
对系统(4)进行变量替换,令=-2,=-2,可得系统(5)。继续对系统(5)进行变换,令=-,=(11+12)/,其中11=-(++2),12=-(2+),经过计算可得:

取第一李雅普诺夫系数为:

则有:
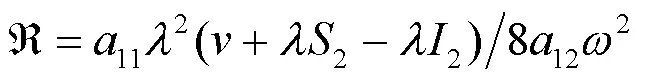
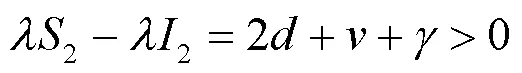
2 数值模拟
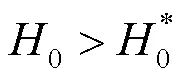

图1 系统(2)不存在极限环
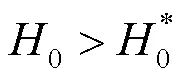

图2 系统(2)存在不稳定的极限环
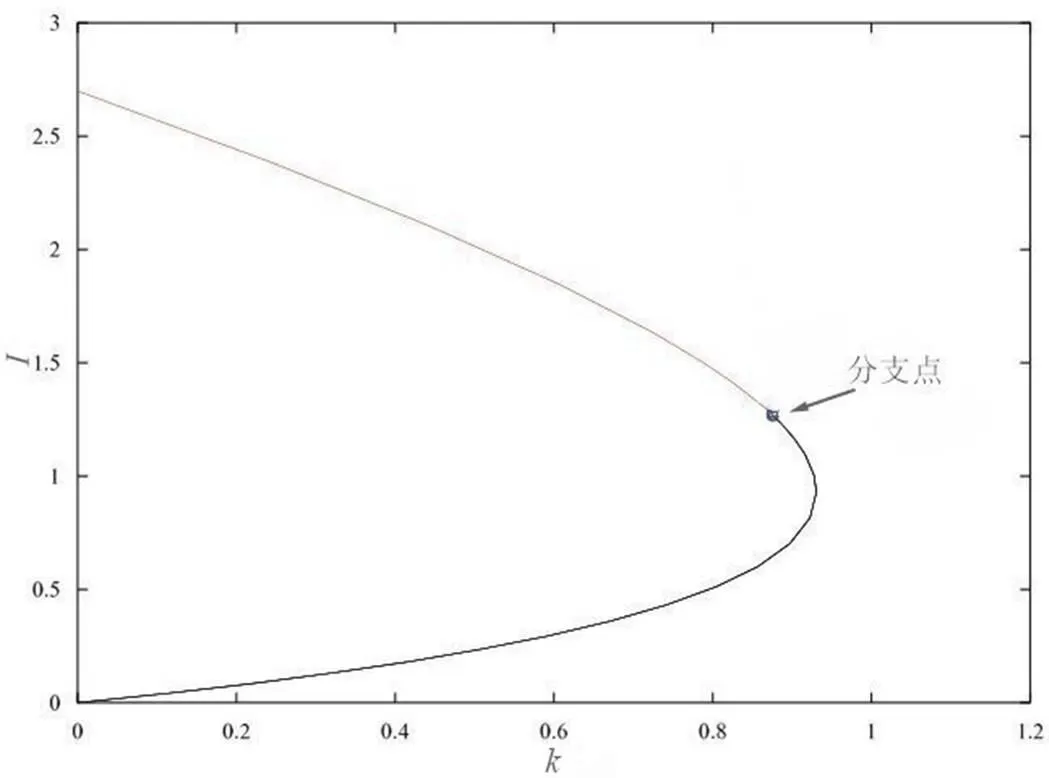
图3 系统(2)的分支点图
3 结束语
[1] 马之恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京: 科学出版社, 2001.
[2] 马之恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004.
[3] ZHOU L.H., FAN M., Dynamics of an SIR epidemic model with limited medical resources revisited[J]. Nonlinear Anal: Real World Appl, 2012, 13: 312-324.
[4] Andersson P, Lindenstrand D. A stochastic SIS epidemic with demography: initial stages and time to extinction[J]. J Math Biol, 2011, 62(3): 333-348.
[5] WANG W.D., Backward bifurcation of an epidemic model with treatment[J]. Math Biosci, 2006, 201: 58-71.
[6] 周美涛. 一类具有双线性发生率与常数治疗函数的SIRS传染病模型的动力学行为[J]. 辽宁工业大学学报: 自然科学版, 2015, 35(5): 344-350.
[7] Alexander M E, Moghadas S M. Bifurcation analysis of an SIRS epidemic model with generalized incidence[J]. SIAM J Appl Math, 2005, 65(5): 1794-1816.
[8] JIN Y, WANG W D, XIAO S W. An SIRS model with nonlinear rate[J]. Chaos, Solitons and Fractals 2007, 34(5): 1482-1497.
[9] Ye Y Q. Theory of Limit Cycles[M]. in: Trans. Math Monogr, vol. 66, AMS, Providence, 1986.
[10] Guckenheimer J, Holmes P J. Nonlinear oscillations,Dynamical Systems,and Bifurcations of Vector Fields[M]. New York: Springer-Verlag, 1996.
Global Analysis of an SIRS Epidemic Model with Treatment Function and Bilinear Incidence Rate
ZHOU Mei-tao
(College of Science, Liaoning University of Technology, Jinzhou 121001, China)
The global dynamics of SIRS infectious disease model with treatment function and bilinear contact rate are analyzed, and the adequacy criterion of the system without limit cycle is obtained through mathematical analysis. When there is no limit cycle in the system, the infectious disease can be eliminated through treatment and control, and the infectious disease will not become endemic; When there is a limit cycle in the system, it is an unstable limit cycle, that is, a subcritical Hopf branch, and the infectious disease can still be eliminated by treatment.
epidemic; limit cycle; global analysis
10.15916/j.issn1674-3261.2023.05.012
O175.1
A
1674-3261(2023)05-0342-06
2022-09-28
周美涛(1987-),男,辽宁朝阳人,讲师,硕士。
责任编辑:陈 明

