基于光电容积脉搏波信号的无创血糖检测系统设计

陈岩　李祥

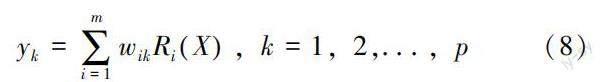
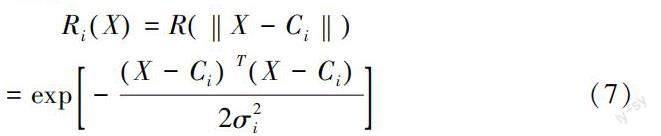
摘要：随着人们生活水平的日益提升，不健康饮食习惯和规律带来的糖尿病患者也随之增加。依赖智能技术实时检测人们血糖的变化十分必要。有创式血糖检测优势在于精度高，劣势在于检测成本高昂且存在医疗风险。为了实现非入侵式血糖检测，无创式血糖检测技术应运而生。为了提高检测精度以及去除噪声等信号干扰，研究结合光电容积脉搏波信号特性对其进行高频滤波并去除基线漂移，之后设计一种改进径向基函数模型来实时监测血糖值。结果显示，该模型在R2指标上取得最高值为0.88，比K-means RBF和PSO-RBF提高了0.10和0.38，这说明该模型面向真实值的预测能力更强。在RMSE指标上，研究所提模型取得最低值为0.55mmol/L，而K-means RBF、PSO-RBF取值分别为0.58mmol/L、0.59mmol/L。对比可知，研究所提模型比之减小了0.03mmol/L、0.04mmol/L。因此，这表明该检测模型精度更高，在血糖检测上具有一定应用潜力。

关键词：PPG，血糖检测，无创，RBF

中图分类号：TN98

文献标识码：A

文章编号：1674-9545（2023）03-0070-（07）

DOI：10.19717/j.cnki.jjun.2023.03.014

近几年，我国糖尿病病人的人数及比重呈上升趋势。糖尿病是一种慢性病，其主要原因是机体对血糖水平的调控作用受到了损害^[1]。胰岛素紊乱可是先天的，也可因食物卫生以及缺少运动所引起的。高葡萄糖会引起严重的并发症，还会损伤肾脏、神经、眼睛、血管等等。葡萄糖浓度过高会引起身体短暂的变化^[2]。糖尿病是一种严重危害人类健康的疾病，现在还不能完全根治。早期糖尿病并无显著症状，只有测定葡萄糖才能确诊。当前，临床上最常用的血糖测定方式是有创伤性血糖测定，即从患者体内提取血浆中提取糖分，然后进行血样测定^[3]。有创葡萄糖测定技术在临床应用中表现出较高的准确性，准确率超95%。但是，有创血糖监测存在费用高、监测不连续等不足。非侵入式的血糖连续监测则是基于血糖改变引起的生理、病理特征改变，能够快速、简便、实时、持续地进行测量^[4]。目前，临床上对糖尿病患者的血糖进行无损测量主要有两种方法：一种是光敏测量法，另一种是非光敏测量法^[5]。当前，人们对光学式血糖的探测方法进行了深入的研究，光学式非创伤血糖探测技术的核心是将具有特定波长的光照射到身体上，当光通过身体的各个部位并与其相互作用之后，入射光的有关特性会被身体的各个部位所影响，因此可以将入射光的频率、相位以及强度等反映出来，从而导致了入射光的特性的改变^[6]。鉴于此，研究基于光电容积脉搏波（photoplethysmographic pulse wave，PPG）信号特征设计一种改进径向基函数（radial basis function，RBF）血糖检测技术来实现实时稳定监测。

1基于PPG信号的无创血糖检测模型构建

1.1 PPG信号预处理及其特征提取

影响PPG信号的干扰源大致分为人体干扰和环境干扰。PPG是一种起伏不定的、非线性的生理学信号，容易受到呼吸、心跳和身体运动等引起的基线漂移的影响^[7]。用来收集 PPG的设备很容易被周围光线、电磁波等因素所影响。大量干扰信号将使得PPG信号变形，变形后的PPG信号无法直接用于血糖检测否则误差太大，因此需要进行信号预处理操作^[8]。PPG信号频率范围是0.1～40Hz，电磁噪声干扰频率高于50Hz，PPG信号频率低，噪声信号频率高^[9]。低频滤波电路结构比较简单，但是在处理复杂的噪声时却显得力不从心。小波分析对模型的精度要求很高，且运算量很大。中值滤波器是用信号中一点在相邻窗内的数值的中值来取代该点数值，以达到去除噪声的目的^[10]。因此，中值滤波稳健性良好，能滤去非独立性噪声。其数学表达式见公式（1）。

式（1）中，Xi表示窗口内数据，XZ表示窗口中位值。MAD表示两者绝对中位差。具体地，PPG信号滑动窗口设置为2k－1个，在信号的两端附加个数为k的端点值，以避免信号在两端有遗失。在一个视窗中，将2k－1个数据由小至大排列，从而获得一个中间数值XZ。高频噪声滤出后，还需要采用3次样条插值去除基线漂移。

式（2）中，x_i表示端点，a_i、b_i、c_i、d_i表示函数系数。所提取的PPG信号被分解为单个周期。将每个周期的波谷作为起点和终点，然后使用3次样条曲线计算匹配的基线。可以通过从PPG信号中减去基线来获取去除基线之后的信号。PPG信号预处理完成后需要进行信号特征提取。公式（3）为综合特征参数R的计算公式。

式（3）中，I^λ_1AC、I^λ_2AC各自表示红光和红外光PPG信号被人体动脉血液吸收的分量。I^λ_1AD、I^λ_2AD各自表示红光和红外光PPG信号被人体肌肉和静脉血液吸收的分量。交流分量是可变的，作为血液量变化的函数，血液量变化表示为PPG的主波和波谷之间的差异。直流分量被表示为平均PPG信号。公式（4）为血糖浓度和综合特征参数R的数学关系式。

式（4）中，C¹表示人体血糖初始值。ε^λ₁₁和ε^λ₂₁表示葡萄糖对波长为λ₁和λ₂的入射光的吸收度。Δl表示血液吸收到最大光强和最小光强状态下的光程差。提取的其他特征包括心率、年齡和身高。心率是评估人类心脏状况的最重要指标之一。根据心率值可以计算出血液输出量和血液流量。血糖变化对心率变异性有重要影响。在检测PPG的过程中，心率的大小可能会影响血糖的量，从而影响血液吸收光的程度。公式（5）为心率计算表达式。

式（5）中，E代表心率，fs代表信号采样频率，numT代表周期数，sumN代表周期数。在将参数进行运算之前，需要先对数据标准化处理。与min-max标准化相比，z-score标准化可以使得原数据转化为无单位数据，从而提高标准化数据的可靠性，因此研究采用标准差标准化方法。公式（6）为z-score标准化数学表达式。

式（6）中，X和Y分别代表原始数据和标准化处理后数据。μ和σ分别代表原数据平均值和原数据方差。

1.2基于改进RBF的无创血糖检测模型建立

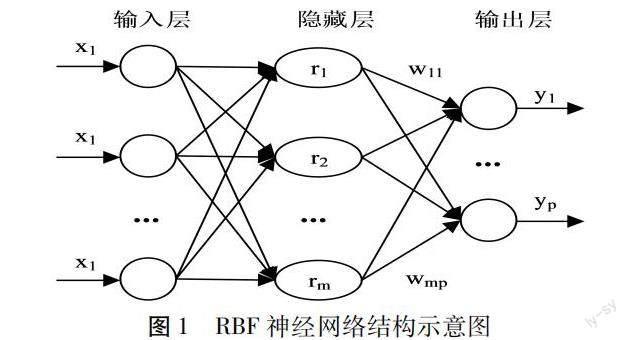
研究将采用RBF模型来寻找特征参数与血糖值之间的关系，从而建立血糖检测模型。RBF神经网络属于单隐藏层的前向神经网络^[11]。使用径向基函数而不是权重链接，可以将输入直接导出到隐藏层中^[12]。在得到隐层基本函数的中心点之后，输入与隐层的关系也将随之确定。因基于权重连接，隐藏层和输出层之间将以线性方式连接。RBF神经网络具有逼近能力强、收敛速度快等特点。图1为RBF神经网络结构示意图。

从图1可知，RBF神经网络由三个层次组成：输入层次、隐藏层次和输出层次。假设输入层、隐含层和输出层的神经元数量分别为n、m和p，输入向量、隐含层向量以及输出向量分别记为X=x₁，x₂，...，x_n^T、R=r₁，r₂，...，r_m^T和Y=y₁，y₂，...，y_n^T。公式（7）为隐含层输出结果计算表达式。

式（7）中，C_i表示第i个径向基函数的中心。σ_i表示第i个径向基函数的宽度。‖X－C_i‖表示范数。公式（8）为输出层输出结果计算表达式。

式（8）中，w_ik表示隐输出层和隐含层之间的权重。考虑到一般的RBF神经网络容易陷入局部求解问题，这将降低模型计算精度和效率。因此，研究采用密度峰值聚类算法（density peak clustering algorithm，DPC）以及动量累加梯度联合优化RBF神经网络，旨在实现精度增益并加快收敛。图2为改进RBF神经网络结构示意图。

从图2可知，然后，DPC算法将分析传入的数据流，并得到集群的密度。按降序排列聚类的集群密度，以便可以选出径向基函数的中心点。DPC算法首先需要计算节点间距离，研究选择欧式距离计算，如公式（9）所示。

式（9）中，a表示维度。x^a_i和x^a_j表示节点i和节点j，dx_i，x_j表示节点间距。dx_i，x_j将与间距阈值进行比较，节点间距小于间距阈值的所有节点将被归为i聚类簇中。基于i聚类簇中其他节点的数量可以定义簇密度，其定义式如公式（10）所示。

式（10）中，ρ_i表示聚类簇i的簇密度。χx表示判断函数，当χx取值为0时，节点j不属于i聚类簇，χx取值为1时，节点j属于i聚类簇。离群点由于与其他节点的距离较大，会使得中心点的簇密度下降带来误差。为了减少异常值的影响，研究使用了中心距离参数，提出了一种新的异常值估计方法。公式（11）为中心点间距以及中心点判别参数计算表达式。

式（11）中，δ_i表示中心点间距，其含义是两个中心点所包含聚类点的间距最小值。γ表示离群点判别参数，该值越小表明节点是离群点的概率越大。传统的梯度下降算法使用人为设置方式^[13-14]。由于人为设置的主观性质，它可能会导致步长过大或过小，并且不能解决模型被困在局部解中的问题^[15]。研究基于动量累加梯度优化传统的梯度下降方法，这使得其具备修正步长的作用。图3为改进算法流程示意图。

从图3可知，该算法首先输入初始参数θ、学习率ε以及样本数据x^_i，然后计算一次计算梯度、累计梯度、累计平方梯度，最后进行参数修正和迭代。公式（12）为梯度估计计算表达式。

式（12）中，g表示梯度估计。y_i表示输出目标。由于动量累加梯度的引入，累积梯度值可以被计算，如公式（13）所示。

式（13）中，v_t表示累积梯度。α表示动量参数。为了加快梯度最小值的搜索速度，梯度需要进行平方化处理。公式（14）为梯度平方化计算表达式。

式（14）中，r表示累积平方梯度。

2基于PPG信号的无创血糖检测模型效用分析

2.1改进RBF模型性能结果分析

实验数据集采用UCI，训练练集规模设置为100，测试集规模设置为50，输入层单元数为4，输出层单元数为1，梯度下降算法中学习率初始化为0.55和动量因子初始化为0.05。

从图4（a）可知，研究所提模型与RBF、PSO-RBF以及K-means RBF相比，在MAE指标上取得了最小值，大小约为0.50mmol/L。迭代过程中，该模型在迭代次数为14时开始收敛，并在迭代次数为18时完成收敛。RBF、PSO-RBF以及K-means RBF开始迭代时间与之相近，但是分别在迭代次数为22、24和24时完成收敛，收敛速度小于研究所提模型。在MAE上，此三种模型取得的收敛值分别为0.57mmol/L、0.55mmol/L和0.54mmol/L。对比可知，研究所提模型在MAE指标上比之减小了14%、10%和8%。从图4（b）可知，起始MAPE数值从高到低依次为10.5%、13.0%、19%和27.5%，分别对应研究所提模型、K-means RBF、PSO-RBF以及RBF。随着迭代次数增加，四种模型MAPE曲线均呈现非线性递减趋势。其中，研究所提模型最早获得MAPE收敛值，大小为5.1%，完成收敛的迭代次数为20。而其余三种模型分别延后了2个、3个和4个迭代次数才完成收敛，对应收敛值为6.8%、7.6%和8.8%。對比可知，研究所提模型在MAPE指标上，比之降低了1.7%、2.5%和3.7%。此外，从曲线波动水平来看，未经优化的RBF波动次数最多，波动幅度最大，研究所提模型以及K-means RBF波动较小。因此，研究所提模型具有更好的相关性和精度。

从图5可知，K-means RBF以及研究所提改进RBF模型的准确率曲线和损失值曲线均呈现相同走向。准确率曲线表现为先增后平，而损失值曲线表现为先减后平。在准确率指标上，K-means RBF模型起始值为40.1%，低于研究所提模型的66.2%；在爬升速度上，研究所提模型在迭代次数为3以后突破90%，在迭代次数为4时突破95%，随后曲线稳定在95%左右，最终在迭代次数为10时获得准确率收敛值为97.5%。而K-means RBF模型在迭代次数为7时才开始收敛，且此时准确率低于90%，当迭代完成时，获得的准确率收敛值为89.3%，依旧低于90%，且比前者低了8.2%。在损失值指标上，K-means RBF模型起始损失值为11.5%，之后当迭代次数下降至5时，损失值减小至6.1%，此时曲线开始呈现收敛趋势，但是仍表现出微小下降趋势，最终在迭代次数为10时，模型取得收敛损失值为5.8%。研究所提模型起始损失值为8.3%，之后同样在迭代次数为5时趋于收敛，转折点对应的损失值为2.7%，随后的迭代中，模型损失值未出现如前者的下降倾向，而是稳定在2.7%附近收敛，最终收敛损失值也为2.7%，比前者减小了3.1%。

2.2基于改进RBF的无创血糖检测模型应用效果分析

为了验证研究采用的基于DPC和动量累加梯度优化的RBF神经网络的有效性，实验选择了100位测试者。测试者之间的身体参数差异较大，每个人采集不同时间段的10组PPG信号，通过PPG信号计算特征参数并结合人体参数构成共320个样本。血糖标准值采用有创血糖仪检测。

从图6（a）可知，研究所提模型R²指标最低值为0.81，最高值为0.88，整体围绕0.84水平线波动，波动幅度最大为0.07。K-means RBF模型R²指标最低值和最高值分别为0.58和0.70，最大波动幅度为0.12。PSO-RBF模型的R²指标值在0.4～0.5之间波动，最高值为0.5。RBF模型R²指标全段低于0.4。决定系数R²描述的是血糖预测值与血糖标准值的相关性，取值在0～1之间。该系数取值越大，预测值对真实值的解释程度越高。当系数低于0.4表明相关性很弱，高于0.7说明相关性较强。因此，研究采用模型取得最高相关性，预测值的解释能力最高，而其余三种模型则相关性相对较低。从图6（b）可知，研究所提模型迭代完成时取得最小RMSE，大小为0.55mmol/L。虽然该模型的RMSE曲线在迭代初期，即迭代次数为6以前RMSE取值较高，但是在迭代中期因为跌落速度较快，于是在迭代次数为9时RMSE降至四种模型最低，此后也一直维持最低位置，并在迭代次数为12时开始收敛，在迭代次数为17时取得最小RMSE收敛值。而K-means RBF、PSO-RBF以及RBF模型在迭代完成时的RMSE收敛值分别为0.58mmol/L、0.59mmol/L和0.64mmol/L。对比可知，研究所提模型比之减小了0.03mmol/L、0.04mmol/L和0.09mmol/L。

从图7可知，改进的RBF模型比未改进RBF取得了更好的拟合效果。当血糖高于6.1mmol/L时，即对于高血糖拟合效果良好，仅在样本数为36时，预测值与实际值之间存在偏差，大小为0.7mmol/L。这表明在高血糖预测上改进RNF模型具有良好跟随性能。而未改进RBF模型则在多处高血糖预测上较大程度偏离真实值，比如当样本数量为32时，偏差为0.85mmol/L；在样本数量为36时，偏差为0.9mmol/L。因此，这表明研究所提的无创血糖检测模型是实际可行的。

3结论

无创血糖检测技術因其简单快捷较之有创血糖检测更具优势，其中的光学式无创检测技术更是研究焦点。鉴于此，文章研究设计了一种改进RBF无创血糖检测模型，以提高检测精度。结果显示，与RBF、PSO-RBF以及K-means RBF相比，研究所提模型在MAE指标上比之减小了14%、10%和8%，在MAPE指标上，比之降低了3.7%、2.5%和1.7%。在准确率指标上，研究所提改进RBF模型比K-means RBF提前4个迭代次数开始收敛，且在迭代次数为4以后便稳定在95%，最终收敛准确率为97.5%，比K-means RBF提高了8.2%。在损失值指标上，该模型比K-means RBF降低了3.1%。此外，研究所提模型R2指标整体围绕0.84水平线波动，波动幅度最大为0.07。而K-means RBF、PSO-RBF均低于0.7，且波动幅度更大，这说明该模型预测值对真实值的解释程度更高。而且改进的RBF模型血糖预测曲线拟合效果更优，在高血糖预测上改进RNF模型具有良好跟随性能。因此，研究所提模型具有优秀的性能和精度，满足连续、实时、无创的血糖检测需求。不过，该研究提取的生理参数有待进一步提高，以便更全面消除人体差异误差。

参考文献：

[1]周聪聪，姚晓天，苏亚，等.基于OCT无创血糖检测的图像校正补偿方法[J].中国激光，2022，49（24）：75.

[2]杨宇祥，吴彬，林海军，等.无创血糖检测技术研究进展[J].分析测试学报，2022，41（4）：578.

[3]龚惠红，王邦辉，胡鑫.近红外光人体血糖无创检测系统设计[J].中南民族大学学报（自然科学版），2022，41（2）：194.

[4]陈剑虹，林志强，孙超越.基于谱分解的无创血糖检测新方法研究[J].光谱学与光谱分析，2021，41（8）：2378.

[5]李孟泽，季忠，程锦绣，等.基于非线性自回归神经网络和双波长的无创血糖测方法实现[J].生物医学工程学杂志，2021，38（2）：342.

[6]Bolla AS，Priefer R. Blood glucose monitoring-an overview of current and future non-invasive devices[J]. Diabetes & Metabolic Syndrome：Clinical Research & Reviews，2020，14（5）：739.

[7]Rassel S，Xu C，Zhang S，et al. Noninvasive blood glucose detection using a quantum cascade laser[J].Analyst，2020，145（7）：2441.

[8]Zhang G，Mei Z，Zhang Y，et al. A noninvasive blood glucose monitoring system based on smartphone PPG signal processing and machine learning[J]. IEEE Transactions on Industrial Informatics，2020，16（11）：7209.

[9]Delbeck S， Heise HM. Evaluation of opportunities and limitations of mid-infrared skin spectroscopy for noninvasive blood glucose monitoring[J].Journal of Diabetes Science and Technology，2021，15（1）：19.

[10]Cebedio MC，Rabioglio LA，Gelosi IE，et al. Analysis and design of a microwave coplanar sensor for non-invasive blood glucose measurements[J]. IEEE Sensors Journal，2020，20（18）：10572.

[11]刘晨沁，袁思念，林高藏，等.基于PPG信号的呼吸监测系统的研制[J].中国医疗器械杂志，2022，46（4）：368.

[12]李嘉玮，张劲，白中博，等.基于多波长光电容积脉搏波采集系统的连续血压测量方法[J].计算机应用，2021，41（S2）：351.

[13]唐姗.临床护士使用便携式血糖检测仪情况的调查[J].中国医疗器械信息，2022，28（18）：149.

[14]蒋亚汶，杨观赐，何玲.家用血糖检测技术研究进展[J].贵州大学学报（自然科学版），2022，39（6）：99.

[15]户丹，张宪华，吴志敏.不同时段动态血糖检测的准确性及其与血糖波动的关系[J].辽宁医学杂志，2022，36（4）：75.

Design of Non-invasive Blood Glucose Detection System Based

on Optical Capacitance Product Pulse Wave Signal

CHEN Yan¹，LI Xiang²

（1.School of medical，Chuzhou City Vocational College， Chuzhou;2. Clinical Laboratory，Chuzhou

Integrated Traditional Chinese and Western Medicine Hospital，Chuzhou， Anhui 239000，China）

ABSTRACT With the improvement of people's living standards， the number of patients with diabetes caused by unhealthy eating habits and regulations also increased. It was necessary to rely on intelligent technology to detect changes in people's blood sugar in real-time. The advantage of invasive blood glucose testing lied in its high accuracy， while the disadvantage lied in its high detection cost and medical risks. In order to achieve non-invasive blood glucose detection， non-invasive blood glucose detection technology had emerged. In order to improve detection accuracy and remove signal interference such as noise， the study first combined the characteristics of PPG signals to perform high-frequency filtering and remove baseline drift. Then， an improved RBF model was designed to monitor blood glucose values in real-time. The results showed that the model achieved the highest value of 0.88 on the R2 index， which was 0.10 and 0.38 higher than K-means RBF and PSO-RBF， indicating that the model has stronger predictive ability towards real values. In terms of RMSE indicators， the proposed model achieved a minimum value of 0.55mmol/L， while the K-means RBF and PSO-RBF values were 0.58mmol/L and 0.59mmol/L， respectively. By comparison， it could be seen that the model proposed by the research institute had decreased by 0.03mmol/L and 0.04mmol/L， respectively. Therefore， this indicated that the detection model has higher accuracy and had certain application potential in blood glucose detection.

KEY WORDS PPG；Blood glucose testing；Non invasive；RBF

（責任编辑 胡安娜）