基于径向基网络的工业机器人误差补偿方法

张 宁，张德权，叶 楠

（河北工业大学机械工程学院，天津 300401）

0 引言

工业机器人广泛应用于汽车、芯片、飞机等自动化生产线中，定位精度作为工业机器人重要的性能指标，直接影响其加工件和装配件的质量。定位精度可分为重复定位精度和绝对定位精度，工业机器人通常具有较高的重复定位精度，但其绝对定位精度比较差[1]。为了高效地驱动工业机器人完成复杂的动作，通常采用离线编程的方式。离线编程是指通过指定工业机器人末端执行器的空间位置来控制工业机器人进行运动，这种控制方式依赖于工业机器人的绝对定位精度。为了提高工业机器人的绝对定位精度，研究者们提出了多种工业机器人定位误差的补偿方法。传统的工业机器人定位误差补偿方法通过运动学参数标定来实现，基本原理是在机器人工作空间中测量几个点的位置误差，依据误差数据确定机器人运动学参数误差并改变机器人运动学模型，其中最常用的工业机器人运动学模型是D-H模型[2]。运动学参数标定法在一定程度上可以提升工业机器人的定位精度，但是该方法存在着一些明显的缺陷。首先，工业机器人位置误差不仅受运动学参数误差影响，而且受负载、温度和重力分布等因素的影响，要建立反映工业机器人实际运动的模型较困难；其次，要在工业机器人非开源系统中更改运动学参数操作不易且代价较高[3]。

近年来，通过代理模型进行误差补偿的方法逐渐受到研究者的重视，该方法将工业机器人视为一个黑盒子，只考虑名义位置和实际位置误差间的映射关系。Cai等[4]采用基于位置误差相似性的普通克里金方法校准离线编程机器人，并通过实验证明了该方法的有效性；Chen等[5]将位置误差相似性原理和误差相关性原理相结合，利用Co-kriging方法估计机器人3个方向的位置误差；Yuan等[6]建立基于极限学习机的位置误差预测模型对位置误差进行预测和补偿，通过实验验证了该方法的有效性。代理模型方法可以考虑到几何因素和非几何因素的影响[3]。常见的代理模型包括响应面方法[7-8]，径向基网络[9-10]，人工神经网络[11]和克里金方法[12-13]等。代理模型的精度越高，误差补偿效果越好。响应面是一种全局回归技术，局部精度较差；克里金模型和人工神经网络模型可获得较好的局部精度但是由于模型训练参数过多，训练过程太耗费时间[14]。

针对上述模型存在的问题，本文提出一种基于粒子群优化的径向基神经网络模型拟合工业机器人名义位置和实际位置误差间的映射关系，构建工业机器人定位误差场，通过预偏移指令位置的方式进行误差补偿。模型训练时间明显缩短，同时拥有较好的局部精度。最后，通过数值算例验证了所提方法具有较高的精确性和工程实用性。

1 工业机器人误差补偿的径向基神经网络方法

1.1 径向基神经网络

径向基函数（Radial Basis Function，RBF）是在1985 年由Powell 提出的一种多维空间插值技术。受到大脑神经元局部响应特征的启发，Broomhead首次将径向基函数引入神经网络。径向基神经网络是一种3层前向神经网络，由输入层、隐含层和输出层组成。径向基神经网络的主要特征是隐含层的激活函数为径向基函数。通用的径向基神经网络结构如图1 所示，xi、hi、yi为分别为输入层节点、隐含层节点、输出层节点，m为输入向量的维数，n为隐含层节点个数，与样本点个数相等，j为输出向量的维数。

图1 径向基神经网络结构Fig.1 The structure of radial basis function neural network

径向基神经网络用一系列基函数的加权线性组合来近似复杂的黑盒子问题，本文中神经网络的输入节点为工业机器人末端执行器的名义坐标位置，即pi=(xi,yi,zi)，输出节点为末端执行器不同坐标方向的位置误差ex(pi)，ey(pi)和ez(pi)。因此，对于工业机器人末端执行器的某待求解点的名义位置pk=(xk,yk,zk)，该点的位置误差可表示为

式中：n为样本点个数；ex(pk)，ey(pk)和ez(pk)为名义位置pk对应3 个坐标方向的位置误差；h(‖pk-pi‖)为第i个隐含层节点的基函数，常见的基函数形式如表1 所示，假设d为两点之间的欧拉距离，c为径向基函数的形参数；ωi1，ωi2和ωi3为隐含层与输出层节点之间的权值。

表1 径向基函数类型Tab.1 Type of radial basis function

以x方向为例，介绍径向基网络训练过程，对于一组样本点p=[p1,p2,…,pnT]，径向基函数的通用表达形式如下

式中：ex(pk)为样本点p对应的x方向位置误差；h(p)为p对应的径向基矩阵，ω1=[ω11,…,ωi1,…,ωn1]T。将样本点代入式（2）中，

式（3）的矩阵形式为

由于H是一个非奇异的矩阵，故式（4）有唯一解ω1=H-1ex，代入式（2）得

根据式（5），即可求得末端执行器每个位置对应的x坐标方向位置误差，剩余2个坐标方向的误差求解与上述方法一致。

对于一般工程问题而言，获得训练样本需要大量时间，因此通常采用交叉验证方法[15]进行模型精度验证。工业机器人定位精度问题获取样本较易，直接通过额外添加样本点来验证模型的精度，并优化形参数c，该优化问题转换为数学表达式为

式中：k为所需额外样本点个数；e(pk)和分别为pk处的实际位置误差和预测位置误差。

上述最小化问题为全局优化问题，采用全局粒子群优化寻找最优的形参数c。粒子群优化算法源自对鸟类捕食行为的研究，由于带有惯性权重的粒子群算法，能够保证较好的全局收敛效果，故本文采用此方法，其进化过程为：

式中：c1和c2为学习因子；r1和r2为[0，1]范围内的均匀随机数；i= 1，2，…，N，N为粒子个数；j= 1，2，…，D，D为搜索空间维数；vij为粒子的速度；xij为当前迭代中的粒子；pij存储第i个粒子目前搜索到的最优位置，即个体极值；pgi存储整个粒子群目前搜索到的最优位置，即全局极值；w为惯性权重，表示在多大程度上保留原来的速度。目前采用较多的是动态惯性权重，表达式为

式中：Tmax表示最大进化代数；wmax和wmin分别表示最大和最小惯性权重；t表示当前迭代次数；一般，取wmax=0.9，wmin=0.4。

采用以下3种评估方式评估模型的精度：均方根误差（RMSE），最大绝对误差（MAX）和多重相关系数(R2)。定义如下：

式中：n表示用于评估模型精度的样本点的数量；yi表示样本点处响应的真实值；yˉ表示其平均值；y^ 表示样本点处响应的估计值。RMSE用来评估模型的全局精度，其值越小，模型的全局精度越高；MAX用来评估模型的局部精度，其值越小模型的局部精度越高；R2用于评价预测值和真实值的线性依赖程度，取值小于1，此值越接近于1 表示预测结果越准确，当R2的值为1 时表示预测结果完全准确。

1.2 径向基神经网络误差补偿方法

通常对机器人进行误差补偿的方式有两种：一种是在关节空间进行补偿；另一种是在笛卡尔空间进行补偿。本文采用第二种方法进行补偿，补偿方法如图2 所示。图2中，p为机器人名义位置，将它输入机器人控制器后反解出各关节转角θi(i=1,2,…,n,n为工业机器人关节数)，但是由于机器人运动学参数存在误差，机器人并未达到名义位置p，而是到达了位置p+Δp。为了补偿运动学参数引起的误差，通过附加算法给工业机器人名义位置一个预偏置-Δp′，名义位置替换为p-Δp′，此时控制器反解出的关节转角变为θi-Δθi，用此转角进行驱动时，预偏置-Δp′与运动学参数误差引起的偏差Δp互相抵消，使工业机器人的定位精度得到提高。但在实际操作时，预偏置-Δp′很难直接求得，考虑用Δp代替-Δp′。当两点之间的距离很接近时，位置误差也会很接近，故此时用Δp代替-Δp′产生的误差|Δp-Δp′|可以忽略不计。

图2 工业机器人误差补偿原理Fig.2 Error compensation principle of industrial robot

在实际补偿实验中，通过拉丁超立方采样方法在工业机器人某工作空间中生成一组位置点，记录并输入工业机器人控制器中，利用激光跟踪仪等测量仪器测量末端执行器的实际位置。计算目标位置和名义位置之间的误差，即3个坐标方向的位置误差。以3个方向的名义位置和位置误差作为径向基神经网络的训练样本以训练神经网络，通过径向基神经网络可以构建名义位置与位置误差的映射关系。对某个名义位置p，利用径向基神经网络都可求得其对应的位置误差Δp。由此可以建立在该工作空间中工业机器人的定位误差场。通过定位误差场，该工作空间中每个目标点位置误差都可求得。得知目标点位置误差后，即可在机器人示教器中直接修改指令位置，缩小实际位置误差。径向基神经网络误差补偿方法的算法流程图如图3所示。

图3 径向基神经网络误差补偿方法流程图Fig.3 Flowchart of RBF neural network error compensation method

2 机器人误差场与误差补偿仿真

本文通过仿真方式验证所提方法的实用性和准确性。首先建立工业机器人的运动学模型，Denavit-Hartenberg（D-H）矩阵描述了工业机器人系统包含位置和方向的运动学方程，D-H矩阵的具体形式如下式：

式中，αi，di，ψi和θi用来定义第i个连杆的坐标。末端执行器的位置可根据式（13）计算：

式中：n，s和a表示建立在末端执行器上的动坐标系相对于基座处固定坐标系的方向余弦；p表示末端执行器在固定坐标系下的位置坐标。

下面以KUKA KR150-2型工业机器人为例，进行误差补偿验证。表2中给出了该工业机器人的D-H参数，根据D-H参数可建立工业机器人的运动学方程。然而，对于某一工业机器人来说，由于加工或者安装误差的存在，D-H参数存在误差，根据文献[16]识别出的参数误差如表3所示。此处仿真实验验证忽略了由于重力分布，负载和温度等因素的影响。

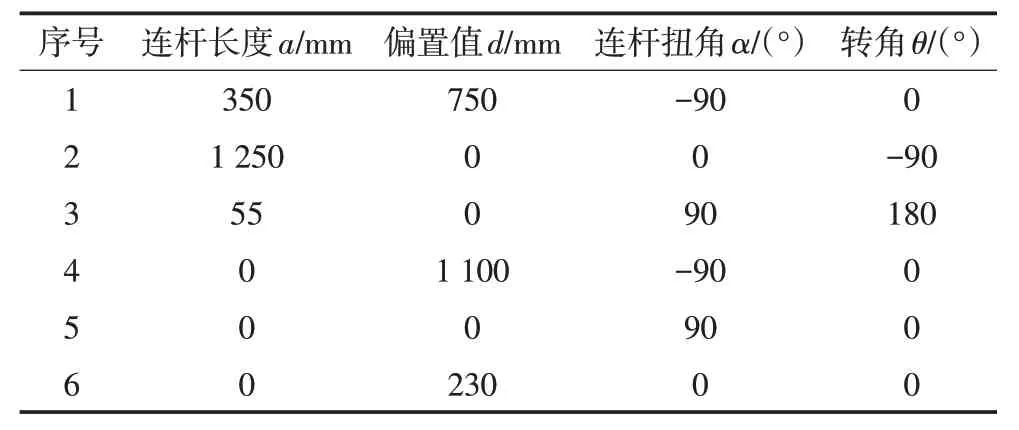
表2 KUKA KR150-2 型工业机器人D-H 模型参数表Tab.2 D-H model parameters of KUKA KR150-2 industrial robot

表3 预给定机器人各运动学几何参数误差Tab.3 The pre-given kinematic geometric parameters error of industrial robot

末端位姿可由T60=A1A2A3A4A5A6求得，为了计算统一，末端位姿矩阵设置为

通过上述机器人模型，已知末端执行器需要到达的位置，即名义位置后，根据无误差运动学方程逆解，可求得各轴转角，再根据有误差的运动学方程求解末端执行器实际到达的位置，即可得到一组包括名义位置和实际位置样本信息。本文中采用Matlab机器人工具箱求解正逆解，生成的工业机器人三维仿真模型如图4所示。依据上述方法，可以通过机器人正逆解构造一系列样本。首先，在机器人工作空间内选取1 m3立方体，在立方体内通过拉丁超立方采样产生350 个末端执行器位置点，分别记录名义位置和实际位置如表4所示；通过计算得到x，y，z3个方向的误差，选取200 个点作为训练样本点，150 个点作为测试样本点，训练神经网络。网络的输入为工业机器人末端执行器的名义位置，输出为实际位置误差。

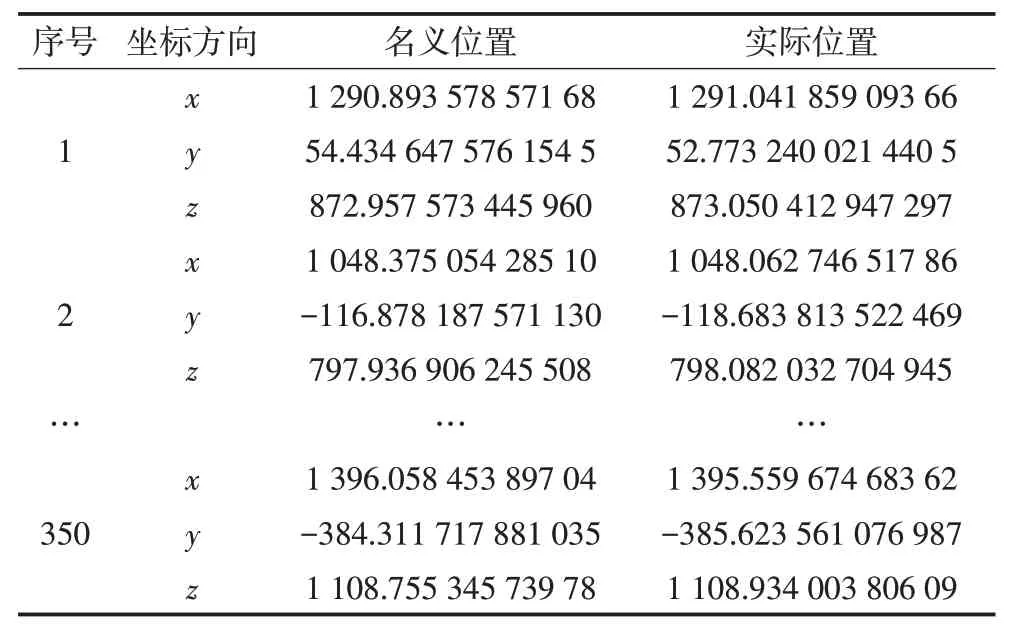
表4 位置点信息（名义位置和实际位置）Tab.4 Positional point information(nominal positional and actual positional)

图4 工业机器人仿真模型Fig.4 Simulation model of industrial robot

以样本点为隐节点中心，训练径向基神经网络，通过粒子群优化得到最优的形参数，对150个测试点进行误差预测，预测效果如图5 所示，图5a），b），c）分别表示x，y，z方向预测误差和实际误差的对比，模型预测精度评价指标统计如表5所示。

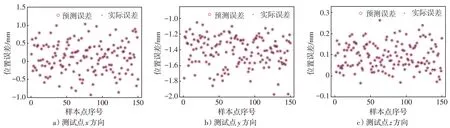
图5 径向基神经网络的预测效果Fig.5 Prediction effect of radial basis function neural network

直观上看，预测误差几乎和实际误差一致，通过表5可看出径向基神经网络的局部精度和全局精度都较高，预测效果最好的方向为z方向。对于不同工业机器人来说，效果最好的方向不一定是固定的。由于150 个测试点是在机器人工作空间随机选取的，径向基网络在测试点的预测精度较高，因此在该工作空间的任意位置预测精度也很高。依此，可以获得整个工作空间的误差情况，如图6 所示，图6a）， b）， c）分别为x，y，z方向定位误差场。工业机器人在特定工作空间中，误差情况不存在突变，这符合位置误差相似性原理。误差场反映的是该工作空间的定位误差情况，依照1.2 节中基于径向基神经网络的误差补偿方法对工业机器人误差进行补偿，补偿前后各个方向的位置误差如图7所示，图7a），b），c）分别为x，y，z方向补偿前后的定位误差对比。

图6 沿三坐标轴方向定位误差场Fig.6 Positional error field along three axes

图7 补偿前后各方向位置误差对比Fig.7 Comparison of position errors in each direction before and after compensation

由图7可看出，任一方向补偿前的位置误差均比较大，补偿以后位置误差趋近于0，这证明了本方法行之有效。从上述数据中可以计算出误差补偿前后总位置误差，总位置误差的计算公式为

式中：ex，ey和ez分别为x，y和z轴3个方向的位置误差；e为总位置误差。补偿前后的总位置误差对比如图8 。通过3 个坐标方向的误差补偿，工业机器人的绝对定位精度得到很大的提升。对于该仿真模型而言，补偿前绝对定位误差为1.5 mm 左右，补偿之后几乎为0 mm。

图8 补偿前后总位置误差对比Fig.8 Comparison of absolute position errors before and after comparison

3 结论

本文提出一种工业机器人误差补偿的神经网络方法，所提方法具有较好的局部精度和全局精度。在径向基神经网络的参数优化中，使用了粒子群优化算法，保证了径向基神经网络的精度。提出了工业机器人定位误差场的概念，描述了工业机器人在某工作空间的定位误差情况。通过仿真实验，验证了所提方法的有效性，很大程度上地提升了工业机器人的定位精度。在仿真实验中，该补偿方法的补偿效果非常好，使工业机器人的定位误差基本接近于0 mm，但是在实际实验中，会有重力，温度和负载等因素的影响，补偿效果有待进一步实验验证。