幂律流体在部分填充多孔介质平板通道内的流动特性研究

徐春晖，陶友瑞，2，段书用，2

（1.河北工业大学机械工程学院，天津 300401；2.河北工业大学电工装备可靠性与智能化国家重点实验室，天津 300401）

0 引言

流体在部分填充多孔介质通道中的流动在微通道热沉、太阳能集热器等工程中有着广泛应用[1-4]。在通道内填充多孔介质可以强化换热，却增加了流动阻力，由于部分填充多孔介质通道有着流动阻力小和换热能力强的特点，于是一些学者对其进行了研究。Shokouhmand等[5]基于局部热平衡单能量方程，分别对多孔介质填充在通道两侧和中间的多孔介质通道的流动与换热进行了研究，结果发现多孔介质填充在通道中间产生的流动阻力和压力降大于多孔介质填充在两侧产生的流动阻力和压力降。另外，Poulikakos等[6]、Maerefat等[7]和Mohamad[8]也分别对这2种填充方式通道内的流动特性进行了研究。Alazmi等[9]研究了5种部分填充多孔介质通道内多孔介质通道和空通道相接的界面条件，结果发现，界面条件对多孔介质通道中的流动影响较大，对换热影响较小，黏度系数对流体的换热和Nu 数的影响不显著。Xu等[10]基于局部非热平衡双能量方程，求解了部分填充多孔介质通道中的无量纲温度和无量纲速度的解析解，并研究了各无量纲参数对多孔介质内流动与换热的影响。Qu等[11]对基于含有边界摩擦阻力项的达西方程和局部非热平衡双能量方程，对泡沫金属填充在环形通道内表面的通道内流动与换热进行了研究，得到了无量纲速度分布得解析解，分析了相关参数对流动特性的影响。匡东升[12]和戴振宇[13]建立了流体在部分填充多孔介质通道中流动的数学模型，并运用有限元数值方法模拟了流体在部分填充多孔介质通道中流动。Yerramalle等[14]在3种界面条件下对部分填充多孔介质圆管通道内的流动进行了研究，结果发现通道尺寸和孔隙率等参数对于流体流动有着显著影响。Lisboa 等[15]基于局部热平衡单能量方程，对部分填充多孔介质平板通道内的对流换热进行了研究。Rodrigues等[16]对部分填充多孔介质的通风腔进行了研究，结果发现多孔介质孔隙率对通风腔流场有着显著影响。目前，部分填充多孔介质流动特性的研究大多针对牛顿流体。在实际工程应用中，流变特性复杂的幂律流体更为常见，针对幂律流体在部分填充多孔介质通道内的流动特性研究更有工程应用价值，但是针对幂律流体的研究较少。本文在以往研究的基础上，通过边界层动量积分法求解了幂律流体的Brinkman-Darcy流动扩展模型，得到了幂律流体在部分填充多孔介质通道内的无量纲速度分布模型。同时，计算并分析了Da数、幂律指数、填充厚度等无量纲参数对无量纲速度分布及峰值的影响。

1 数学物理模型

如图1所示，2个无限长的平行板通道之间的距离为H，部分填充了均匀多孔介质，其中未填充多孔介质部分的距离为H1。幂律流体在平板通道中单向流动。幂律流体单相不可压缩，并且除流体粘度外，其它物理参数是定值。假设重力效应没有影响。此外，流动进入充分发展阶段。

图1 幂律流体流经部分填充多孔介质通道的示意图Fig.1 Flow diagram of power law fluid in partially filled porous media channel

对于部分填充多孔介质平板通道，需要使用2 种控制方程来分别描述幂律流体在多孔介质通道（填充均匀多孔介质区域）和空通道（未填充多孔介质区域）的流动行为。多孔介质通道的动量方程和空通道的动量方程分别为

式中：u为幂律流体流速；μ为幂律流体稠度系数；ε为多孔介质孔隙率；n为幂律流体的幂律指数；K为多孔介质渗透率；为轴向压力梯度。

为求解式（1）、式（2），引入如下无量纲参数：

则式（1）、式（2）无量纲形式为

对应的无量纲边界条件为

边界层黏性阻力只存在于边壁附近的边界层。在边界层之外，无量纲中心线速度如下：

由式（9）可得无量纲压降为

对式（3）在通道上动量积分得

式（3）、式（4）的对应边界条件如下：

为了求解式（3）、式（4），需要在多孔介质区域与未填充多孔介质区域交界处和多孔介质区域与边壁交界处两个边界层中分别添加速度分布经验公式。假设边界层中速度呈二次抛物线分布，则无量纲速度分布的表达式为

式中，

将边界条件式（12）～式（18）代入式（19）可得到

由此，无量纲速度为

通过将抛物线速度分布表达式（19）代入到式（3）、式（4）中并考虑到边界条件式（12）～式（18），获得了无量纲边界层厚度：

式中，Γ是伽玛函数。

体积平均速度um和无量纲体积平均速度Um的定义如下：

由此，可得无量纲体积平均速度

因此，基于体积平均速度的无量纲速度为

联立式（21）、式（23）、式（24）、式（26）和式（27），采用迭代法求解，即可求得无量纲速度。

2 计算结果分析

2.1 无量纲速度分布的影响因素分析

根据定义的无量纲参数，可知道Y1为空通道的无量纲厚度，(1-Y1)为多孔介质通道的无量纲厚度。文献[4]未考虑多孔介质通道与空通道交界处的边界黏性阻力，并且在n=1（即牛顿流体）条件下求得了速度分布的解析解。为了验证当前解的正确性，在n=1 和Da=0.000 01 的条件下，图2 将本文速度模型与文献[4]中给出的数据进行了比较。

图2 本文速度分布与参考文献的对比Fig.2 Comparisons among the present date te and the ones given in references

图3 所示为Y1=0.2，n=1 时，达西数Da对无量纲速度分布的影响。由图3 可以看出，多孔介质通道(Y＞Y1) 内的无量纲速度明显低于空通道(Y＜Y1)内的无量纲速度，速度峰值出现在空通道内。随达西数Da减小，多孔介质通道内速度减小，空通道速度增大。当Da＜10-5时，达西数Da的变化对无量纲速度不再有显著的影响，无量纲速度分布基本不变；此时边界层厚度极小，通道内的无量纲速度趋于达西流，动量方程中的边界层粘性阻力项对无量纲速分布的影响几乎可以忽略，即在Da＜10-5时，直接使用达西定律来描述幂律流体在多孔介质通道内的流动更加简便。

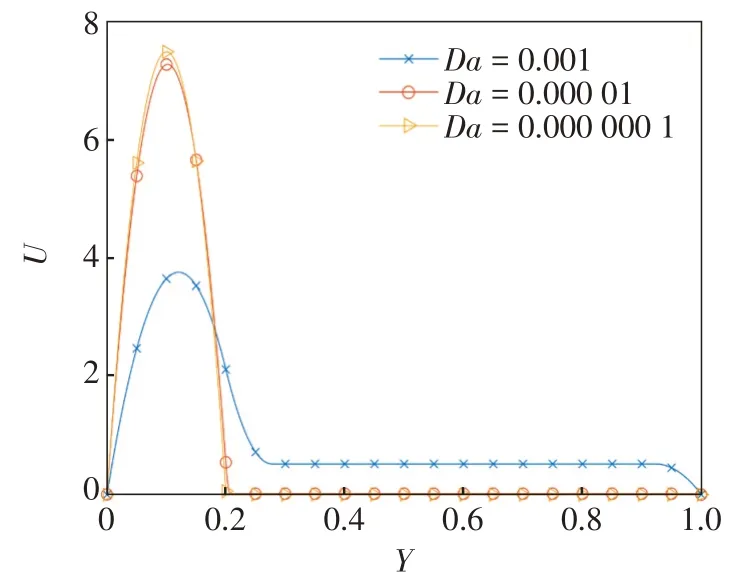
图3 达西数Da对无量纲速度分布的影响Fig.3 The effect of Darcy number on dimensionless velocity distribution

图4为Da=0.001，n=1时，多孔介质填充厚度对无量纲速度分布的影响。随着空通道厚度Y1增加，空通道(Y＜Y1)无量纲速度先增大后减小。这是由于当空通道厚度较小时，随着空通道厚度增加空通道内的流量也显著增加，流速自然升高。在部分填充多孔介质平板通道内，由于流动阻力有差距，空通道内单位厚度的流量大于多孔介质通道，尤其是在达西流区（一般认为Da≤0.001），达西数Da越小流量差距越大，因而当空通道内无量纲厚度达到一定值后，大部分幂律流体均在空通道内流动，流量随无量纲厚度增加的变化将不再显著，即随着无量纲厚度的增加，空通道内流量迅速增加，而后增加越来越平缓。因此当空通道达到一定厚度时，随着空通道无量纲厚度增加，流量增加不再明显，流速反而降低。多孔介质通道(Y＞Y1)流速随着多孔介质通道厚度(1-Y1) 的减小而降低，这是由于多孔介质通道厚度的减小导致空通道厚度增大，使得空通道的流动阻力减小，流体通过空通道内的流量增加，因此通过多孔介质通道内的流量减小，流速减小。Y1=0 表示两平板之间完全填充了多孔介质，流动呈结构流特征，流核速度稳定，边界层速度由边壁到流核逐渐增大。

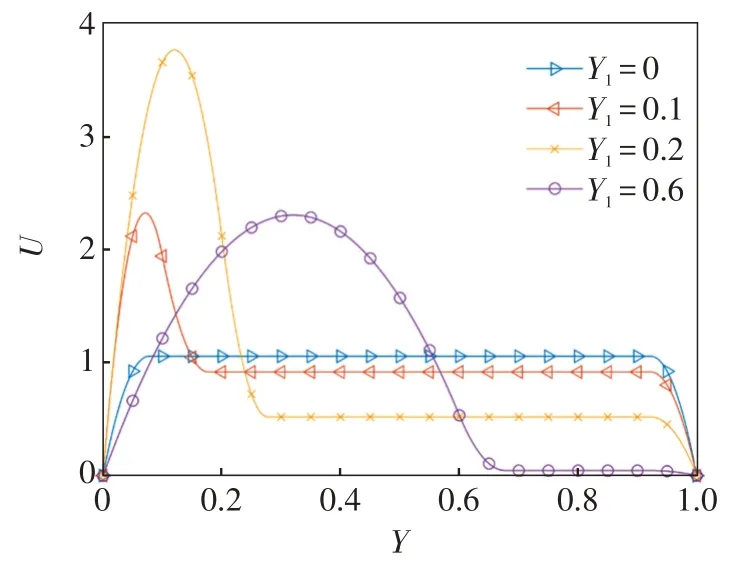
图4 填充多孔介质区域厚度(1-Y1 )对无量纲速度分布的影响Fig.4 The effect of porous media thickness on dimensionless velocity distribution

图5描述了在Y1=0.2 及达西数Da=0.001的条件下，部分填充多孔介质通道内的无量纲速度分布随幂律指数n的变化情况。从图5 可知，剪切变稀流体（n＜1）在空通道(Y＜Y1)内的无量纲流速比剪切变稠流体（n＞1）和牛顿流体（n=1）高，即随着幂律指数n的减小，空通道内的无量纲流速增大。剪切变稠流体（n＞1）在多孔介质通道(Y＞Y1)内的无量纲流速比剪切变稀流体（n＜1）和牛顿流体（n=1）高，即随着幂律指数n的增大，多孔介质通道内的无量纲流速增大。在空通道内流动阻力小于多孔介质通道内的流动阻力，幂律流体在空通道内的无量纲速度明显高于多孔介质通道内的无量纲速度。由于剪切变稀流体随速度增加而表观粘度降低，空通道内的速度高，因而流动粘性阻力进一步减小，流速进一步增大；在多孔介质通道内情况相反。

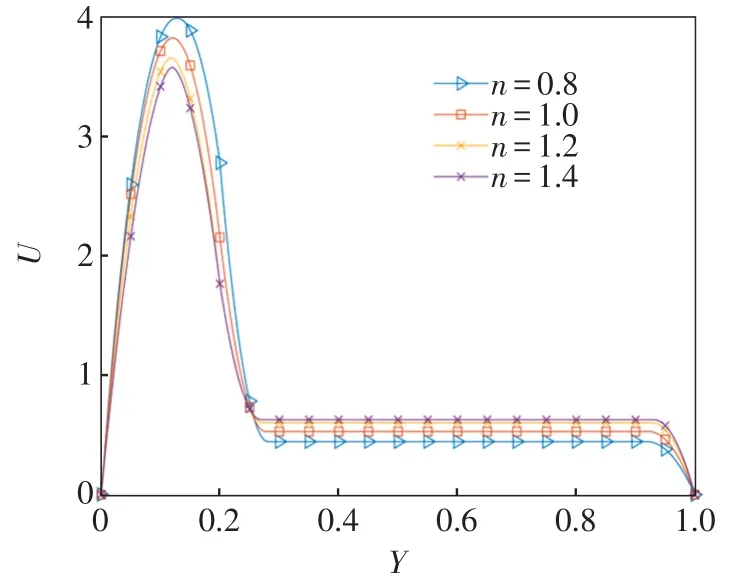
图5 幂律指数n 对无量纲速度分布的影响Fig.5 The effect of power law index on dimensionless velocity distribution

2.2 无量纲速度峰值的影响因素分析

图6描述了在幂律指数n=1的条件下，达西数Da对无量纲速度峰值Umax的影响，无量纲速度峰值Umax一般在空通道内。分析图6可知，随着空通道厚度Y1增加，无量纲速度峰值Umax先增大后减小，并且变化越来越平缓。在同样的填充厚度下，当Y1≤0.4时，随达西数Da减小，无量纲速度峰值Umax增大，因为达西数Da减小会使得多孔介质通道内流动阻力增加，幂律流体则被挤入流动阻力更小的空通道内，导致空通道内的无量纲速度峰值增加。当Y1≥0.4时，速度峰值Umax随达西数Da变化幅度较小，几乎可以忽略，这是由于随着空通道的厚度增大与多孔介质通道厚度的减小，进一步导致空通道的流量增大而多孔介质内的流量减小，但由于空通道厚度较大时，空通道内的流量远大于多孔介质通道，即大部分流体在空通道内，此时流量增加量很小。因此空通道厚度较大时，幂律流体由于达西数Da减小被挤入空通道流量有限，对空通道内的速度分布影响较小，速度峰值Umax变化不大。

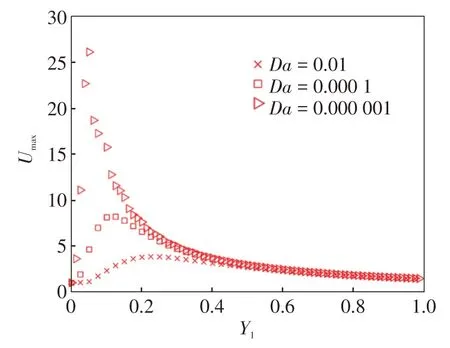
图6 达西数对速度峰值的影响Fig.6 The effect of Darcy number on dimensionless maximum velocity

图7描述了在达西数Da=0.001的条件下，幂律指数n对无量纲速度峰值Umax的影响。分析图7可知，随着Y1增加，无量纲速度峰值Umax先增大后减小。当空通道厚度较小时，剪切变稀流体（n＜1）在空通道内的无量纲速度峰值比剪切变稠流体（n＞1）和牛顿流体（n=1）高，即随着n的减小，空通道内的无量纲速度峰值增大。因此，当多孔介质填充厚度较厚即空通道厚度较薄（约Y1≤0.3）时，流速因流量增大而增大，由于剪切变稀流体随速度增加而表观粘度降低，进一步提高了流速；当空通道厚度增大（约Y1≥0.3），流量增加有限，流速反而因厚度增大而减小，由于剪切变稀流体随速度减小而表观粘度降低增大，进一步降低了流速。

图7 幂律指数n 对速度峰值的影响Fig.7 The effect of power law index on dimensionless maximum velocity

3 结论

通过边界层动量积分法求解了幂律流体Brinkman-Darcy 流动模型的动量方程，得到了幂律流体在部分填充多孔介质通道内的无量纲速度分布模型。计算分析了达西数Da、幂律指数n和填充厚度等无量纲参数对无量纲速度分布和速度峰值的影响。

1）随着达西数Da减小，空通道(Y＜Y1)内的无量纲流速增大，多孔介质通道(Y＞Y1) 的无量纲流速降低，当达西数Da≤10-5时，达西数Da对无量纲速度分布的影响不再显著。增加空通道（即未填充多孔介质区域）厚度Y1，空通道内的无量纲流速先增长后降低，多孔介质通道内的无量纲流速降低。剪切变稀流体（n＜1）在空通道内的无量纲流速比剪切变稠流体（n＞1）和牛顿流体（n=1）高，即随着n的减小，空通道内的无量纲流速增大；多孔介质通道情况相反。

2）增加空通道厚度Y1，无量纲速度峰值Umax先增大后减小，最后趋于平稳。随着达西数Da减小，无量纲速度峰值Umax增大，当Y1≥0.4时，速度峰值Umax随达西数Da变化幅度较小，几乎可以忽略。多孔介质填充较厚时，随着幂律指数n减小，无量纲速度峰值Umax增大，多孔介质填充较薄时则相反。无量纲速度峰值Umax随达西数Da的变化比随幂律指数n的变化更明显。