参与微电网频率调节的光伏发电系统模糊自适应功率控制
李忠文, 吴龙, 程志平, 贾东强, 孙浩锋
(1.郑州大学 电气与信息工程学院,河南 郑州 450001; 2.国网河南省电力公司许昌供电公司,河南 许昌 461000)
0 引 言
近年来,随着人类对清洁能源需求和环境保护意识的不断提高,光伏、风能等新能源在世界范围内得到了快速发展[1]。由于光伏(photovoltaic,PV)发电具有可再生、无噪声、易控制和成本逐年降低等优点,因此在微电网中迅速发展[2]。然而,PV发电通常采用电力电子变换器与电网连接,导致电网系统的惯量和阻尼特性降低。PV大规模接入微电网会降低系统的抗干扰能力和调频能力[3],微电网系统的安全稳定运行将面临巨大挑战[4]。为了解决在高PV渗透率下,系统的低惯量和低阻尼特性等问题,电力行业迫切需要PV发电系统能够有效参与微电网的频率调节[5-6]。
针对高PV渗透给电力系统带来低惯量和低阻尼特性的问题[7],国内外学者提出了一系列解决方法。例如微电网安装储能系统[8-9]、调节需求侧负荷和消减供电侧PV发电量[10]等。基于微电网安装储能系统的方法,PV阵列通常运行在最大功率点追踪(maximum power point tracking,MPPT)模式,系统只能通过储能装置参与微电网频率的调节[11-12]。该方法虽然能够双向抑制频率的波动,但目前储能设备使用寿命较短且安装和维护成本较高[13-14],不易大规模采用。基于调节需求侧负荷的方法,通常根据PV发电量实时调节非关键负荷的离/并网状态[15]。然而,该方法容易导致负荷反复投切和能源利用率不高的问题。基于PV消减的方法,通常将PV阵列偏离最大功率点运行,使PV保留一定的功率储备,通过改变PV有功输出可快速提供频率响应[16]。与上述调频方法相比,该方法有更迅速的响应速度和更低的经济成本。因此,本文计划研究PV自适应发电控制策略,通过自适应调节PV发电量参与微电网频率的调节。
主要教学内容:自主选择企业,运用课程知识,系统解决在现场遇到的实际问题。教学地点:实习基地或就业单位。教学课时:14周。
基于PV消减的调节策略具有成本低、稳定性强、算法简单等优点,国内外学者近几年给予密切关注。其中文献[17]提出了一种消减功率—电流曲线的功率储备控制策略,该策略不需要传感器就能够跟踪不同天气条件下给定的功率储备比。然而,该算法比较复杂,在实际应用中不易实现。文献[18]提出了双有功—频率下垂控制算法,该算法能够根据频率变化的幅度和速度改变下垂特性进行频率调节。然而,该算法需要增加小型PV模型并测量其开路电压或短路电流,增加了模型复杂性和系统成本。文献[19]采用时间序列分析方法,对PV发电系统进行建模,通过时间序列模型预测太阳辐照度,这将增加系统的计算量和响应时间。文献[20]提出了变减载参与微电网频率调节的控制方法,该方法结合离线拟合和在线功率跟踪,根据电网频率波动改变减载率,能够双向调节系统的频率。然而,离线曲线拟合存在不准确性,可能导致频率调节出现偏差。文献[21-22]通过对微电网中控制增益和调频参数的设计研究。然而,随着电网情景的变化,上述参数需要不断重新设置。文献[23]通过对高PV渗透率下电网动态频率特性的研究,对电网动态频率恶化趋势提出应对措施。文献[24]通过设计PV并网逆变器的控制策略,实现PV阵列参与微电网频率调节。但对系统稳定性的影响和虚拟惯量时间常数的整定有待进一步研究。
模糊控制器具有强鲁棒性,不需要精确的数学模型,易于设计等优点[30],该控制策略被广泛用于解决电力系统的电压频率控制问题。文献[25]采用模糊控制策略监测储能系统的荷电状态并决策出当前双向DC-DC变换器的参考电流进行调频,然而设计的模糊控制器为五隶属度函数,与本文提出的七隶属度函数模糊控制策略相比控制精度较低。文献[26]采用基于模糊PID的下垂控制策略代替传统下垂控制策略以补偿风电场参与调频对电力系统总惯性的影响。然而,系统加入的自动电压调节回路与频率控制之间存在弱耦合,影响系统的稳定性。文献[27]提出一种基于频率信号的模糊控制对孤岛微电网能量管理的监督控制,模糊控制器通过调节PV产生的功率和辅助机组的补充功率来抑制频率的波动。但该研究仅局限于微电网的孤岛模式,并不适用微电网并网运行的情景。文献[28]提出了一种自适应分数阶模糊控制策略,对动态完全未知的交流微电网系统进行频率控制,此方法采用神经网络,粒子群和人工蜂群等算法进行参数优化,这增加了系统的响应时间和计算复杂度,并容易陷入局部最优。文献[29]提出了一种具有智能学习PV贡献的自适应模糊下垂模型,以减小系统变化引起的微电网频率偏移问题。但这种方法需要辐照度传感器、最大功率点(maximum power point,MPP)估计器和储能系统,增加了系统的投资和维护成本。文献[30]提出一种基于模糊控制的PV发电和电动汽车并网的频率控制策略,但该策略没有考虑电力系统中的参数不确定性问题。针对上述研究的不足,本文提出光伏发电参与微电网频率调节的模糊自适应功率点追踪 (fuzzy adaptive power point tracking,FAPPT)控制策略,不需要MPP估计器、储能系统和详细的PV模型,通过控制PV输出功率指令实现PV阵列自适应降功率运行,使PV发电有效参与微电网频率的双向调节。
Spearman相关分析显示,舟山市ILI周发病人数与前4周平均气压、周日照时数和前2周平均极大风速呈正相关 (r=0.180、0.258和 0.170,P均<0.05),与周平均降水量和周平均相对湿度呈负相关(r=-0.266 和-0.180,P 均<0.05),而与周平均气温、周平均最高气温、周平均最低气温、周平均日温差、周平均水汽压、周平均风速均无线性相关关系 (P>0.05),见表 2。
1 光伏发电控制策略
1.1 Buck-Boost型DC/DC变换器控制
由于Buck-Boost型DC/DC变换器具有较宽的电压调节范围,可升降电压幅值,而PV阵列经常受到环境影响导致其输出电压幅值高于或低于电网电压幅值,PV阵列并网时需通过Buck-Boost型DC/DC变换器调节PV阵列输出电压幅值使其等同于电网侧电压幅值。因此,采用Buck-Boost型DC/DC变换器进行调压。Buck-Boost型DC/DC变换器运行在FAPPT模式下的控制策略如图1所示。FAPPT模式是通过模糊控制器[32]自适应调节PV阵列的功率输出,其详细介绍由下文2.1节给出。调节原理由下式得:
(1)
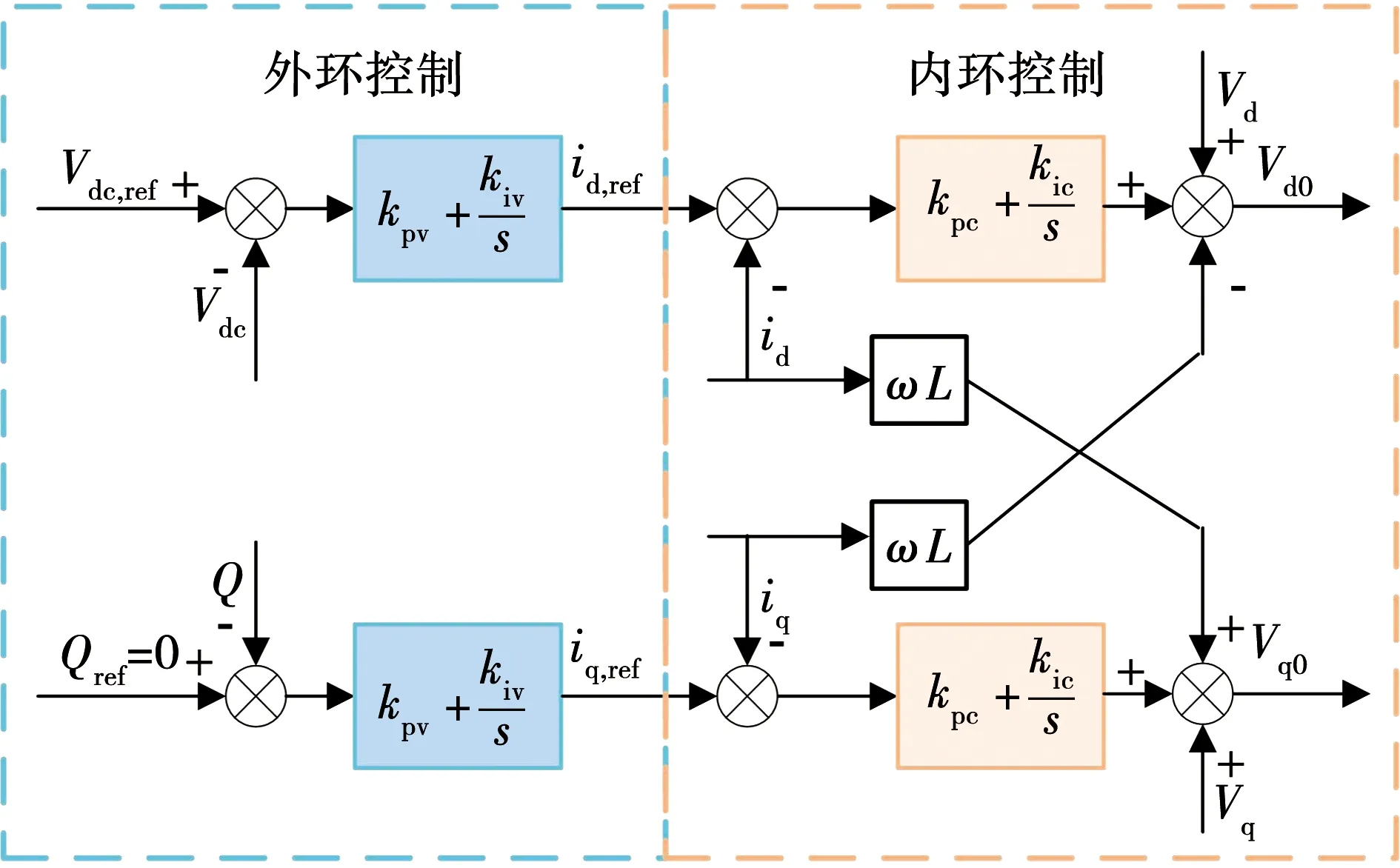
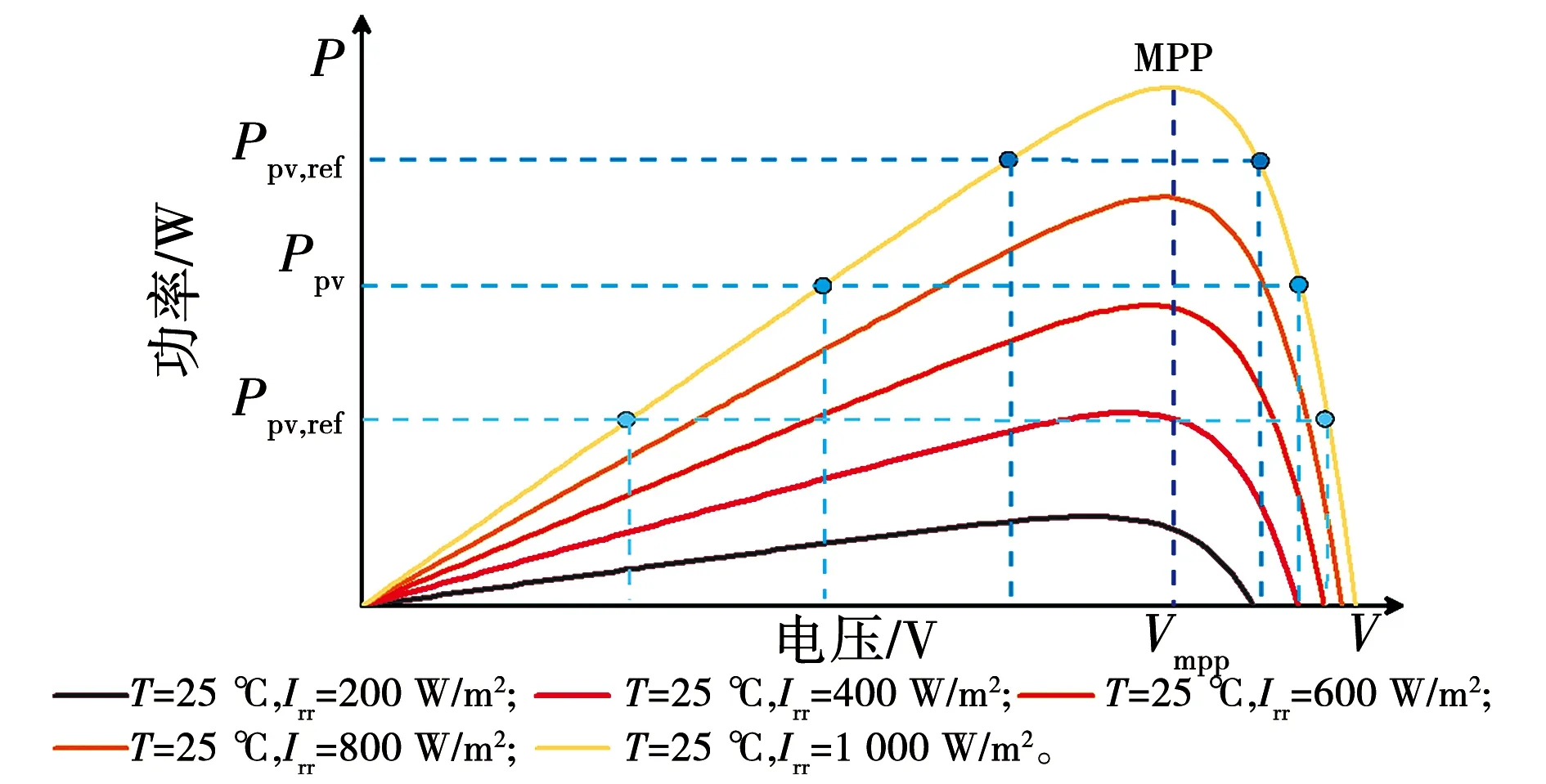
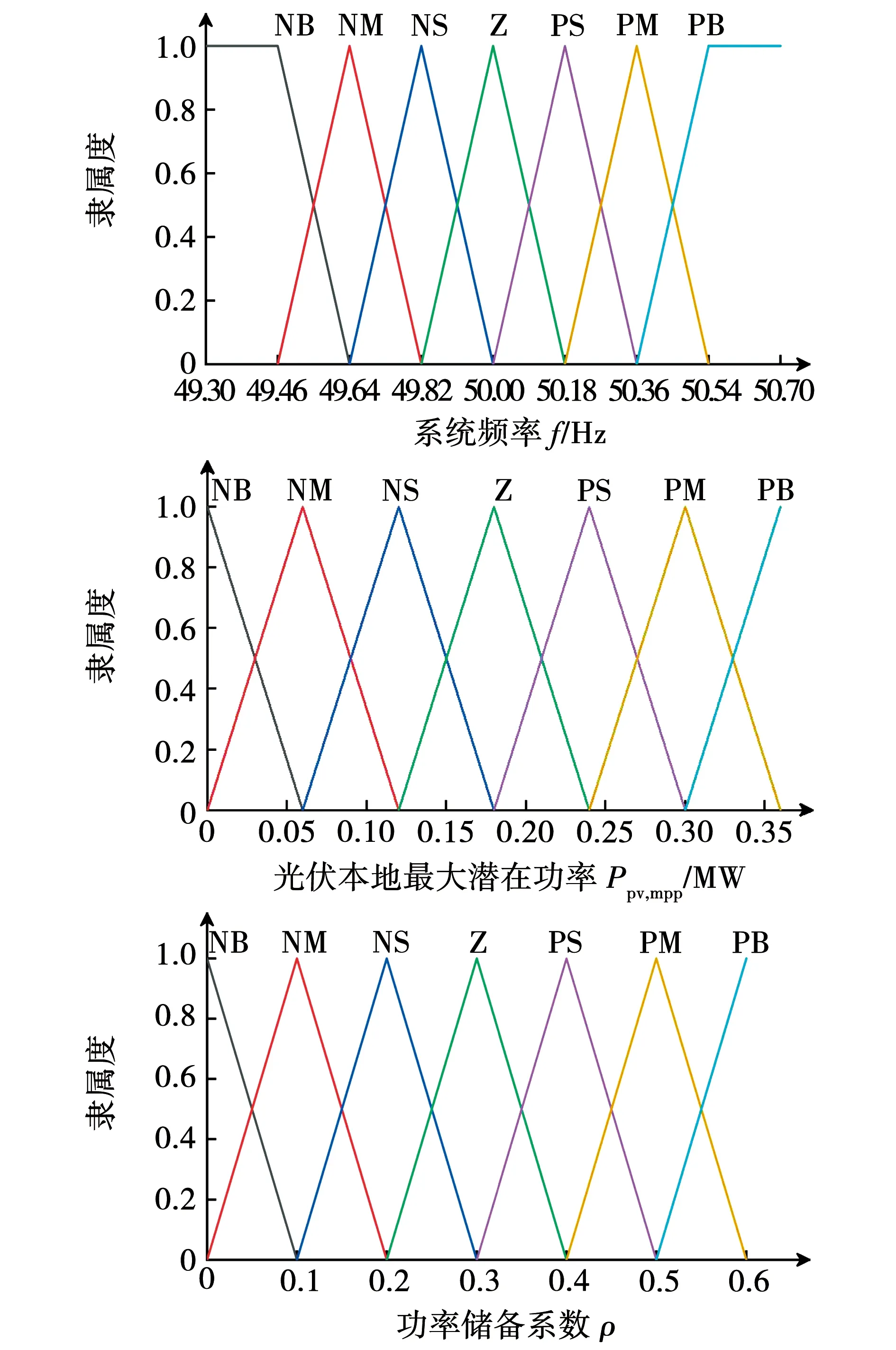
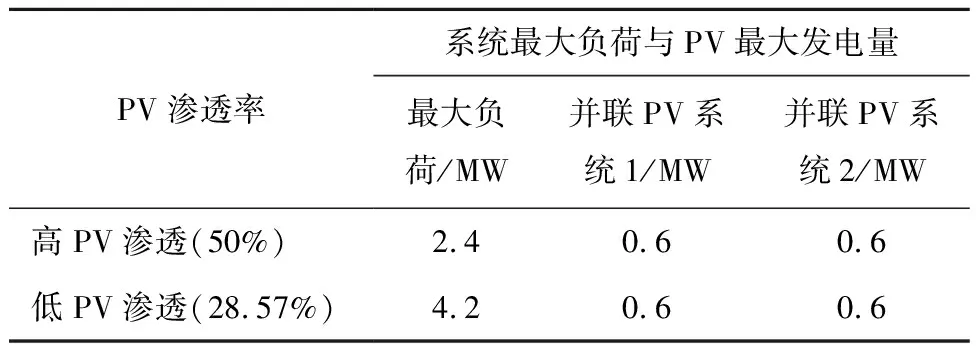
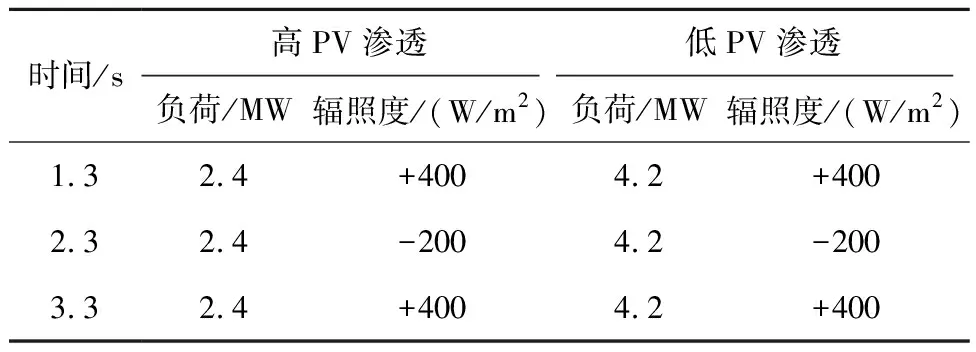
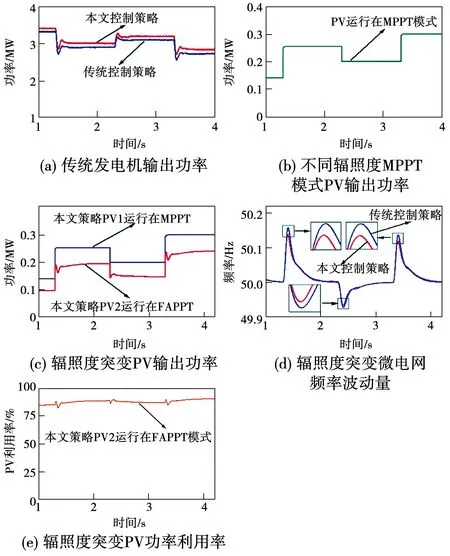
式中:当充电占空比D=0.5时,DC/DC变换器输入电压Vin和输出电压Vo其值相等,DC/DC变换器不升压也不降压;当充电占空比为0 图1中,首先通过采集PV阵列电压Vpv和PV阵列电流Ipv计算出dIpv/dVpv,然后再与参考功率Ppv,ref共同输入到FAPPT控制器中得到PV电压参考指令Vpv,ref。接着通过基于PI电压电流环控制器调节PV阵列的实际电压追踪参考电压Vpv,ref,产生电压信号U。最后通过PWM控制器生成控制信号调节Buck-Boost型DC/DC变换器。Buck-Boost型DC/DC变换器在MPPT模式运行时,控制结构与图1相似,只需将FAPPT算法替换为对应的MPPT算法即可。 通过DC/AC并网逆变器将DC/DC变换器的直流输出转换为交流输出,PV阵列才能集成到交流微电网中。通常情况下,控制DC/AC逆变器的目的是为了稳定直流链电压和调节无功[33]。为了实现这一目的,在dq旋转参考系中采用基于PI的矢量控制策略控制DC/AC并网逆变器[34],其矢量控制器结构如图2所示。图2由外部直流链电压/无功控制环和内部电流控制环构成。在dq旋转参考系中,外部d轴控制环控制直流链电压或有功功率,而外部q轴控制环控制无功功率。内部电流控制环通过调节公共耦合点处的实际电流id、iq来追踪外部直流链电压/无功控制环产生的参考电流id,ref、iq,ref,实现控制DC/AC并网逆变器。 图2 DC/AC并网逆变器控制原理图Fig.2 Control schematics of grid-connected DC/AC inverter 根据传统电导增量MPPT控制算法和文献[35],本节设计出改进的MPPT控制算法。PV电池在不同辐照度下的P-V特性曲线如图3所示。在图3中,设环境温度T=25 ℃恒定,给出5个不同Irr数据,图中Irr曲线从上往下依次减小200 W/m2,其图3中最上面曲线的Irr为1 000 W/m2,光伏MPP会随着Irr的减小而降低,本节以光照强度Irr=1 000 W/m2为例进行分析,当PV阵列运行在MPPT时应满足 图3 不同辐照度PV功率—电压特性曲线Fig.3 Photovoltaic power-voltage characteristic curves of different irradiance (2) 根据式(2)可推导出 改进电导增量MPPT算法的参考电压Vpv,ref调整规则参考文献[35]。 In order to have better insight into the operation of the proposed MOSFET structure, the physics based compact analytical model of the surface potential and threshold voltage has been presented in this section. (3) 其中:Vpv、Ipv分别表示PV阵列的输出电压和输出电流;Ppv表示PV阵列输出功率。PV阵列运行在MPP时,则dPpv/dVpv=0,推出电导关系为 (4) (5) 其中:sat()表示饱和函数;H=dPpv/dVpv;系数α>0,β>0。式(5)采用饱和函数sat()代替文献[35]的符号函数sgn()。其中饱和函数sat()为: Unity3D是一款面向组件的开发引擎,一个工程由多个场景构成,每一个场景中的所有物体都被称为游戏对象,对每一个游戏对象来说,通过对其添加组件的方式来实现游戏对象的各种功能,即游戏对象的所有功能都要通过组件来实现。脚本是一种特殊的组件,通过添加到游戏对象上来实现用户自定义的一些功能。在设计一个游戏对象的具体功能时,可以将组件分为3个层次,从低到高分别为:基础组件,指的是Unity3D提供的内部功能组件,如物理组件、声音组件、渲染组件等;模块功能脚本组件是通过脚本实现的、相对独立的、可重用的功能模块组件;高层的整合代码脚本,这些脚本将引擎基础组件和模块功能组件整合到一起,实现最终游戏对象逻辑。 (6) 在微电网中的PV阵列通常运行在MPPT模式,导致系统频率稳定性变差,为了使PV发电能够有效参与微电网频率的调节,本文提出一种FAPPT控制算法。PV阵列采用FAPPT算法可以偏离最大功率点运行,从而提供一定的功率储备,以便系统频率波动时能够自适应改变有功输出参与频率调节。为了实施上述控制策略,设计了图4所示控制结构,其中每两簇PV阵列为一组,每簇PV阵列通过一台前级Buck-Boost型DC/DC变换器建立直流母线电压,然后每相邻两台Buck-Boost型DC/DC变换器并联后通过DC/AC逆变器接入微电网。图4中1号Buck-Boost型DC/DC变换器采用1.3节提出的电导增量MPPT控制算法使PV阵列运行在MPPT模式;2号Buck-Boost型DC/DC变换器采用本节提出的FAPPT控制算法运行。运行在MPPT模式的1号DC/DC变换器可以从PV阵列中汲取最大光伏输出功率。假设两簇PV阵列地理位置相邻,一般情况下具有相似的辐照度及温度条件。因此,通过测量1号DC/DC变换器的PV阵列运行在MPPT模式下的最大输出功率,可以获得2号DC/DC变换器的PV阵列运行在FAPPT模式下的可用最大功率参考指令[36-37]。这种结构具有不需要辐照度传感器和MPP估计器的优点。运行在FAPPT模式的PV阵列将保留一定的功率储备,并根据给定参考功率Ppv,ref实时补偿微电网功率不平衡,来参与微电网频率双向调节。 其中:ep=Ppv,ref-Ppv;kp和ki分别为PI控制器的比例系数和积分系数。 (7) 表6数据显示sig=0.000实验组和对照组平均值为4.92和0.98,说明两组差距显著,使用移动终端软件学习词汇有多种输入方式和方法,据调查,沪江开心词场的APP软件包括了真人发音,英翻汉,汉翻英,选词填空,等多种练习方式,以游戏或者竞赛的方式进行。而传统学习方式完全依靠学生自身的学习方式创造性,而很多练习需要另外一个人配合才能完成,实行起来难度较大。 其中γ为饱和函数的系数,定义Δ为0.001。 图4 PV发电系统的控制结构Fig.4 Control structure of a PV generation system 针对以上情况,本项目对下横梁同步及异步施工工艺对塔柱受力的影响进行分析复核,并采取在下横梁上部塔柱上增设主动水平横的辅助措施。 Ppv,ref=(1-ρ)Ppv,mpp。 (8) 其中:ρ表示功率储备系数,取值范围为0≤ρ≤0.6;Ppv,mpp表示本地PV阵列最大潜在发电功率参考,由于相邻PV组之间的辐照度、温度等环境条件非常相似,因此认为相邻PV组每单位的本地最大潜在功率Ppv,mpp相同。通过测量运行在MPPT模式下PV阵列的输出功率,即可得到运行在FAPPT模式下PV阵列的本地最大潜在功率Ppv,mpp。因此,PV阵列运行在FAPPT模式时无需辐照度传感器及MPP估计器,可降低系统的运行和维护成本,并且可以避免MPP估计器所带来的功率预测误差。 由图3光伏功率—电压特性曲线可得,PV阵列最初输出功率Ppv可能高于或低于参考功率Ppv,ref。当PV阵列输出功率Ppv≤Ppv,ref时,PV阵列运行在MPPT模式并增加有功输出,直到PV阵列输出功率Ppv=Ppv,ref时,PV阵列从MPPT模式切换到FAPPT模式。当Ppv>Ppv,ref时,FAPPT控制算法通过以下2种情况进行设计。 基于上述分析,当Ppv>Ppv,ref时,定义提出的模糊自适应PPT控制算法的控制变量为 (9) 根据式(5)可定义PV参考电压Vpv,ref为 雷钢,带妹妹进卧室去。雷志雄说。雷钢和雷红,没叫一声妈妈,连看也没看她一眼,便进了卧室。雷钢,雷红。见儿女们不认,她急了,高声喊。雷钢和雷红仍没反应,像没听到似的,或者压根儿就没她这个妈妈。雷钢还把房门也关了起来。她疯了似地扑过去,想把门推开,里面早被雷钢扣起来了。雷钢,雷红,我是你们妈妈,妈妈想你们,开开门让妈妈看看你们。一边哭一边喊。 为实现MPPT控制模式到FAPPT控制模式的无缝切换,需要保持2个控制器的积分器状态始终同步。以上提出的MPPT控制算法和FAPPT控制算法无缝切换流程图如图5所示。 教育研究中,主要关心的是两个或多个变量之间是否存在某种关系.例如,个体的数学阅读成绩与逻辑思维能力之间是否存在内在联系?单凭经验,人们可以认为两者之间有联系,但是从研究的角度看,必须要用一定的方法和数据去验证它们之间的确存在内在联系.相关性研究,就是处理这类问题的一种方法. 图5 MPPT算法与FAPPT算法无缝切换流程图Fig.5 Seamless switching flowchart of the MPPT algorithm and the FAPPT algorithm 在PV系统中,根据当前系统频率特性和本地最大潜在功率状态值来响应调频需求是一个非常复杂的过程,其数学模型难以精确建立,由于模糊逻辑控制无需精确的数学模型[30],故本节提出了功率储备系数模糊自适应调节算法,该算法可以实时补偿系统功率不平衡,维持微电网频率的稳定。 5)考虑到海洋环境条件,控制系统及其设备在设计时应适应倾斜、摇摆、冲击、颠震等海况条件(具体的数值应根据不同海域情况加以考虑).同时还应该考虑盐雾、霉菌等的影响. 模糊控制器根据当前输入的频率和光伏功率决策出功率储备系数ρ,功率储备系数模糊自适应控制结构如图6所示。图6中,模糊控制器的输入为当前系统频率f和当前PV阵列最大潜在功率Ppv,mpp,输出为功率储备系数ρ,再通过式(6)计算出参考功率Ppv,ref,然后PV阵列根据参考功率Ppv,ref实时调节有功输出,即可参与微电网系统频率的双向调节。由于交流电力系统的频率变化应保持在额定值±1%以内[38],考虑到一些不可预测事件的发生,取模糊控制器的输入频率f为(49.3~50.7 Hz)。设单组PV阵列最大发电量为0.3 MW,考虑到一些极端天气及环境条件的变化,取模糊控制器的输入功率为(0~0.3 MW)。功率储备系数ρ选取规则为:当频率偏离额定值且越来越大时,模糊控制器输出的功率储备系数ρ会随之增大;当频率偏离额定值且越来越小时,模糊控制器输出的功率储备系数ρ会随之减小。根据式(6),当Ppv,mpp值较大时,ρ值较小的改变将会引起PV阵列输出功率较大的改变;当Ppv,mpp值较小时,ρ值较大的改变引起PV阵列的输出功率变化较小。因此,当Ppv,mpp值较大时系统频率发生波动,模糊控制器输出的功率储备系数ρ变化相对较小;当Ppv,mpp值较小时系统频率发生波动,模糊控制器输出的功率储备系数ρ变化相对较大。输出变量功率储备系数ρ的取值范围为(0~0.6)。 模糊控制器的输入变量和输出变量对应关系及隶属度函数如图7所示(输入变量和输出变量均采用三角形隶属度函数),模糊规则推理表如表1所示。根据当前系统频率f和当前PV阵列最大潜在功率Ppv,mpp,建立模糊规则的推理原则:当输入频率f非常小且当前PV阵列最大潜在功率Ppv,mpp非常小时,则输出功率储备系数ρ非常小;当输入频率f非常小且当前PV阵列最大潜在功率Ppv,mpp非常大时,则输出功率储备系数ρ略小;当输入频率f适中且当前PV阵列最大潜在功率Ppv,mpp适中时,则输出功率储备系数ρ适中;当输入频率f非常大且当前PV阵列最大潜在功率Ppv,mpp非常大时,则输出功率储备系数ρ略大;当输入频率f非常大且当前PV阵列最大潜在功率Ppv,mpp非常大时,则输出功率储备系数ρ非常大。 表1 模糊控制器逻辑规则表Table 1 Logic rule table of fuzzy controller 图7 模糊控制隶属度函数Fig.7 Membership functions of fuzzy controller 系统当前频率f、PV阵列当前最大潜在功率Ppv,mpp及功率储备系数ρ都包含7个模糊子集。其中NB、NM、NS、Z、PS、PM、PB分别表示负大、负中、负小、零、正小、正中、正大。 为了验证所提控制算法的可行性和有效性,在MATLAB/Simulink环境下搭建仿真模型。其拓扑结构采用标准IEEE13节点模型,如图8所示。仿真模型由1个传统发电机,2个逆变器,4组PV阵列和若干负荷组成。系统采用分层控制结构,其中第一层采用有功—频率下垂控制,第二层采用基于PI的频率恢复控制。根据设计的结构,当两组并联PV阵列的其中一组运行在MPPT模式,另一组运行在FAPPT模式时,定义为采用提出控制策略进行运行。当两组并联PV阵列都运行在MPPT模式时,定义为采用传统控制策略进行运行。 图8 IEEE13节点仿真系统单线图Fig.8 Single line diagram of IEEE13 node simulation system 为验证所提控制策略在不同PV渗透率下的性能,采用两种PV渗透情景进行研究,参数如表2所示。PV渗透率定义为PV装机容量与最大负荷的比值。PV利用率定义为PV系统实际发电功率与最大可发电功率的比值。为便于FAPPT控制算法参数的设计,在不同渗透率下PV装机容量保持不变。考虑到用电侧负荷的不断变化及PV阵列周围环境的随机性改变会影响系统频率的稳定性,因此通过设定负荷突变和辐照度突变来模拟频率波动事件。 表2 不同渗透率下最大发电容量 MPPT控制算法的控制变量可用式(5)表示,其中式(5)的积分项参数选取α=2 000,β=2 000。提出的FAPPT控制算法的控制变量用式(7)表示,其中式(7)包含的PI参数根据比例积分调节规则选取kp=1e-3,ki=1.5e-2。 相邻并联的两组PV阵列运行模式如图8所示,其中一组运行在MPPT模式,另一组运行在FAPPT模式。由于光伏并联系统1和光伏并联系统2采用的算法、结构、模型、容量相同,环境因素非常相似,则光伏并联系统1的PV1和PV2仿真结果与光伏并联系统2的PV3和PV4仿真结果相同。因此,只展示光伏并联系统1中PV1、PV2的结果进行分析。 目前,语篇教学成为大学英语阅读教学的主流。思维导图的应用可以让学生根据既有的知识结构和阅读经验对全文做总体把握,使得阅读教学避开了 “先词汇、后语法、再阅读”的传统套路,实现了“自上而下”的阅读教学模式。实践证明,思维导图是一种实用、有效的阅读工具和教学手段,思维导图的应用有利于提高阅读效率、改善教学成效。 为了评估不同功率储备系数对系统性能的影响,仿真情景设置如下:高PV渗透率下,辐照度Irr=1 000 W/m2恒定,温度T=25 ℃恒定,t=1.3 s时,负荷突减0.69 MW,t=2.3 s时,负荷突增0.69 MW,功率储备系数取值分别为0、0.1、0.2和0.3;其功率储备空间取值范围分别为0~0、0~0.2、0~0.4和0~0.6。 图9和图10展示了不同PV渗透率情景下,提出的控制策略在不同功率储备系数下的性能分析。从图9(a)和图10(a)可知,功率储备系数取值越大,PV2输出功率越低,其弃光量也越多,但有更多的功率储备参与调频。当t=1.3 s负荷突减时,PV2迅速降低有功输出,功率储备系数取值越大下降的功率越多,是因为功率储备系数取值大PV阵列有更多的功率储备来参与系统的频率调节;当t=2.3 s负荷突增时,PV2迅速增加有功输出,功率储备系数取值越大增加的功率越多。从图9(b)和图10(b)可知,当t=1.3 s负荷突减时,系统频率突增,功率储备系数取值为0.3时的频率突增量最小;当t=2.3 s负荷突增时,系统频率突减,功率储备系数取值为0.3时的频率突减量最小。因此,采用的功率储备系数取值越大,提出的控制策略频率调频能力越强,其弃光量也越多,综合考虑PV系统调频能力及弃光量,以下研究的功率储备系数取值设定为0.3。 图10 低PV渗透下不同功率储备系数取值范围时的微电网系统性能分析Fig.10 Performance analysis of the PV system under different power reserve coefficient value range when the MG is with low PV penetration 为了评估负荷突变对系统性能的影响,仿真情景设置如下:辐照度Irr=400 W/m2和Irr=1 000 W/m2两种情况,温度T=25 ℃恒定,不同辐照度下负荷突变情况如表3所示,其中+表示负荷突增,-表示负荷突减。 图11和图12分别展示了高PV渗透和低PV渗透率情景下,提出的控制策略与传统控制策略在负荷突变条件下的性能对比。由图11和图12可知,t=1.3 s负荷突减时,传统发电机迅速降低有功输出,参与系统的频率调节;而PV1、PV2稳定运行在MPPT模式,其有功输出仅与辐照度有关,不参与系统频率调节。当光伏并联系统采用提出的控制策略时,由图11(a)(c)(e)和图12(a)(c)(e)可知,t=1.3 s负荷突减时,PV2降低有功输出抑制频率的波动,此时传统发电机频率波动量明显低于传统控制策略下的频率波动量;而传统发电机有功输出迅速降低后再小幅度升高,是因为传统发电机参与了系统的一、二次调频。t=2.3 s负荷突增时,PV2增加有功输出抑制频率的波动,此时系统频率波动量明显低于传统控制策略下的频率波动量。t=3.3 s时辐照度上升到1 000 W/m2,从图11(d)、(f)和图12(d)、(f)可知,提出的控制策略同样能够有效抑制负荷突变引起的频率波动。从图11(g)、(h)和图12(g)、(h)可知,当系统稳定时,PV利用率维持在85%附近;当负荷突增时,PV利用率接近100%。不同渗透率、不同辐照度及不同负荷波动情景下,系统频率波动量对比如表4所示。因此,提出的控制策略能够有效的为微电网提供双向频率调节。 基于上述分析,对于FAPPT控制算法,定义PV阵列输出功率参考Ppv,ref为 表4 负荷突变系统频率最大波动值 图11 高PV渗透下电导增量MPPT算法与FAPPT算法在负荷突变条件下的性能对比Fig.11 High PV penetration performance comparison with the incremental conductance MPPT algorithm and the FAPPT algorithm under varying load conditions 图12 低PV渗透下电导增量MPPT算法与FAPPT算法在负荷突变条件下的性能对比Fig.12 Low PV penetration performance comparison with the incremental conductance MPPT algorithm and the FAPPT algorithm under varying load conditions 为了验证PV阵列发生故障时的调频能力,设计如下仿真情景:高PV渗透率下,辐照度Irr=1 000 W/m2恒定,温度T=25 ℃恒定,t=4.3 s时,负荷突增0.69 MW,t=5.3 s时,负荷突减0.69 MW。1) 设定PV1发生故障,其中有40%的PV板不能发电,PV2正常;2) 设定PV1正常,PV2发生故障,其中有40%PV板不能发电。 缩颈通常会发生在冲孔过程或者钢筋笼下放前期,导致钢筋笼无法顺利到达设计位置。缩颈现象产生的主要原因是塑性土壤的遇水膨胀,在塑性土壤中冲孔时可能会遇到缩颈现象的产生。 图13(a)、(b)和图13(c)、(d)分别展示了PV1有40%的PV板不能发电和PV2有40%的PV板不能发电。从图13(a)可得,PV1发生故障时的输出功率低于PV2无发生故障时的输出功率。从图13(b)可得,在t=4.3 s负荷突增和t=5.3 s负荷突减时,PV1发生故障时的调频能力低于PV2无故障时的调频能力。是因为PV1发生故障时,PV1的最大参考功率比实际的小,会减低PV1的调频能力。从图13(c)可得,PV2发生故障时PV2的输出功率低于PV1无发生故障时的输出功率。从图13(b)可得,在t=4.3 s负荷突增和t=5.3 s负荷突减时,PV2发生故障时的调频能力低于PV1无故障时的调频能力。是因为PV2发生故障时,PV2的最大参考功率比实际的小,会减低PV2的调频能力。 1.2.8 质量改进 对QCC活动开展3个月、6个月进行质量评定;针对变化,圈员再b次开展讨论,结合现场查看验证,绘制鱼骨图,目标锁定于床单位擦拭方法与医疗废物处置缺陷率高。 图13 高PV渗透下PV阵列受光照不均匀以及局部阴影等因素影响时的性能分析Fig.13 Performance analysis of the PV system under uneven illumination or local shadows when the MG is with high PV penetration 在某一个转子位置,为了评估辐照度变化对系统性能的影响,在微电网辐照度突变时,保持系统负荷恒定。仿真情景设置如下:初始辐照度Irr=400 W/m2,温度T=25 ℃恒定,辐照度突变情况如表5所示,其中+表示辐照度突增,-表示辐照度突减。 表5 负荷恒定时辐照度突变时间表 图14和图15分别展示了高PV渗透和低PV渗透率情景下,提出的控制策略与传统控制策略在辐照度突变条件下的性能对比。 图14 高PV渗透电导增量MPPT算法与FAPPT算法在辐照度突变条件下的性能对比Fig.14 High PV penetration performance comparison with the incremental conductance MPPT algorithm and the FAPPT algorithm under varying irradiance conditions 图15 低PV渗透电导增量MPPT算法与提出的FAPPT算法在辐照度突变条件下的性能对比Fig.15 Low PV penetration performance comparison with the incremental conductance MPPT algorithm and the FAPPT algorithm under varying irradiance conditions 由图14(b)和图15(b)可知,传统控制策略下的PV1和PV2运行在MPPT模式时能够快速准确的追踪到最大功率。t=1.3 s辐照度突增,由图14(a)、(b)和图15(a)、(b)可知,光伏并联系统采用传统控制策略时,传统发电机有功输出迅速降低,只有传统发电机参与系统频率的调节;而并联的PV1、PV2阵列始终运行在MPPT模式,不参与系统频率的调节。由图14(a)、(c)和图15(a)、(c)可知,并联PV系统采用提出的控制策略时,PV2偏离最大功率点运行,此时留出较大的功率储备抑制系统频率的波动,而传统发电机需要增加输出功率补偿PV2在FAPPT模式下产生的功率储备。当辐照度突变时,PV2通过改变功率输出抑制系统频率的波动。由图14(d)图15(d)可知,当光伏并联系统采用提出的控制策略时,辐照度突变引起的频率波动明显低于传统控制策略下频率的波动低且频率稳定性得到显著的改善。从图14(e)和图15(e)可知,当系统负荷稳定时,PV利用率一直维持在85%附近;当辐照度变化引起系统频率波动时,PV发电参与调频的同时仍保留一定的功率储备防止负荷突变引起频率波动。不同渗透率、不同辐照度波动和负荷恒定情景下,系统频率波动量对比如表6所示。因此,提出的控制策略能够有效地为微电网提供双向频率调节。 表6 辐照度突变系统频率最大波动值 本文针对高PV渗透率下,微电网系统频率响应能力不足的问题,提出了光伏发电参与微电网频率调节的模糊自适应功率控制策略。该策略采用IEEE13节点微电网测试系统进行仿真分析,仿真结果与传统最大功率点算法相比,所提控制策略能够快速有效地抑制微电网频率的双向波动。此外,本文所提控制策略减少了辐照度传感器和MPP估计器的使用,无需详细的PV模型,易于实现;该策略还有更好的控制性能,提高了系统频率稳定性和PV发电接入能力,并减小了系统最大频率偏差。因此,PV发电系统与微电网连接时,不仅能够给负荷提供功率,还承担微电网频率调节的任务。本文着重研究了PV发电参与微电网频率调节的暂态特性,其长时间尺度下稳定性及经济性分析是今后研究的重点。1.2 DC/AC并网逆变器控制
1.3 改进电导增量MPPT算法

2 自适应功率点追踪算法
2.1 自适应算法的设计

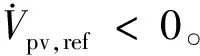
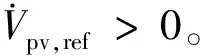

2.2 模糊控制器的设计

3 仿真分析

3.1 不同功率储备系数时的系统性能分析

3.2 负载突变工况下系统调频效果分析




3.3 辐照度突变工况下系统调频效果分析


4 结 论

