基于Markov链随机脉宽调制的永磁同步电机高频边带谐波与声振响应抑制

陈勇, 邱子桢, 马凯, 孔治国, 黄炘

(1.广西大学 机械工程学院,广西 南宁 530004; 2.中汽研新能源汽车检验中心(天津)有限公司,天津 300300)

0 引 言

当前,在环境保护与清洁能源快速发展的背景下,以电动汽车和混合动力汽车为代表的新能源汽车成为未来汽车产业发展的趋势。永磁同步电机(permanent magnet synchronous motor,PMSM)以其高转矩/功率密度、高转速、操作与控制灵活等优点,广泛用于电驱动总成[1]。然而,由于缺少了传统发动机的掩蔽效应,电机本体振动及其辐射噪声对动力总成系统的运行稳定性、可靠性及整车层面的NVH(noise,vibration,harshness)性能均有重要的影响[2]。特别是,由电压源逆变器(voltage source inverter,VSI)及空间矢量脉宽调制策略(space vector pulse-width modulation,SVPWM)所引入的高频边带谐波成分,导致边带电流谐波集中在载波频率及其整数倍范围内,从而导致电机辐射出高频率、令人感到不适的“啸叫”[3-4]。

诸多研究文献中采用解析与有限元数值计算的方法[5],分析并识别了边带谐波成分的时空分布与幅值特征。通过构建电磁场、电机本体结构、振动响应与声辐射的多物理场预测模型,基于模态叠加与边界元法的声振有限元与半解析仿真模型[6],实现了从电磁谐波到机械响应之间的多物理场耦合,能够实现高精度的电机声振响应预测。解析法[7]可以更快、更直接地反映“机电磁控”多物理量之间的耦合关系。通过对VSI所输出的PWM波进行傅里叶级数分解,考虑基本的电磁参数与结构尺寸,可以构建定子与转子坐标系下的边带谐波电流解析模型,并运用麦克斯韦张量法以实现对径向电磁力幅值、频率次数与空间阶次的完整解析[8]。

通常,SVPWM的载波频率被设定为固定值,对于边带谐波及声振响应的抑制主要围绕基于Parseval原理的扩频调制技术,即令信号在时域和频域内的能量保持不变,通过扩大谐波分布频谱范围,达到降低谐波幅值的效果[9-10]。根据信号种类,扩频调制策略可以分为基于周期性信号和离散随机性信号两种方式。文献[11-12]中,对基于三角波和正弦波的两种扩频调制效果进行了分析,尽管周期性扩频调制技术可以使原先固定的载波频率以确定且可控的方式进行变化,但边带谐波与声振抑制效果有限。在诸多随机性调制技术中,以离散随机信号的脉宽调制(random pulse-width modulation,RPWM)技术应用最为广泛,离散的随机信号可以与SVPWM技术相结合,使PWM输出脉冲宽度呈现随机化,使原本集中的边带谐波能量扩展至较宽的频域范围,从而实现抑制边带谐波和声振响应幅值的效果[13]。相比于传统的PWM和SVPWM,RPWM能够有效降低谐波畸变率(total harmonic distortion,THD)[12]、抑制转矩脉动[9]、降低电机铁损等,特别是有效降低低频侧与高频侧边带谐波成分[14]。

然而,考虑到离散的随机数序列在硬件上实现的难易程度,常规RPWM通常采用以线性同余法或查表法为主的伪随机数生成方法[15]。与理想随机数相比,伪随机数在局部时间段内会大于或小于数学期望值,从而导致所生成的随机化载波频率呈现出连续大于或小于初始载波频率的现象[16]。RPWM所生成的不均衡随机数会直接影响谐波抑制效果,使边带谐波不能最大化抑制,而且会使系统输出信号中产生较大的电流纹波,从而导致输出转矩波动及产生额外的开关损耗[14]。

为改善随机数性能以进一步优化边带谐波电流与振动噪声的抑制效果,本文引入多状态Markov链算法。首先,对SVPWM所引入的边带电流谐波与径向电磁力进行解析分析,并通过样机实验对相电流与声振响应的频谱进行特征识别。其次,分别建立多状态Markov链算法的随机数生成策略模型;计及转移概率与随机增益参数对抑制效果的影响,结合粒子群算法进行随机参数寻优。最后,通过策略搭载与样机实验,对比分析稳态工况与不同转速工况下边带电流谐波与声振响应实验结果,进一步验证多状态Markov链优化算法的有效性。

1 基于SVPWM的边带成分特征识别

1.1 边带电流谐波与径向电磁力特征解析

常规SVPWM可以被等效为对称放置零矢量的常规采样PWM,其输出相电压被视作调制波与载波频率调制的结果[17],如图1所示,y(t)为调制波,Ts为采样周期。以第一载波频段为例,边带电流谐波可以通过在定子坐标系框架中构建以调制波频率f0和载波频率fc为变量的双重傅里叶级数,再通过坐标变换重新排列转子坐标系中的边带谐波分量直接解析[5]。位于第一载波频率频带范围内的边带电流谐波可以表示为

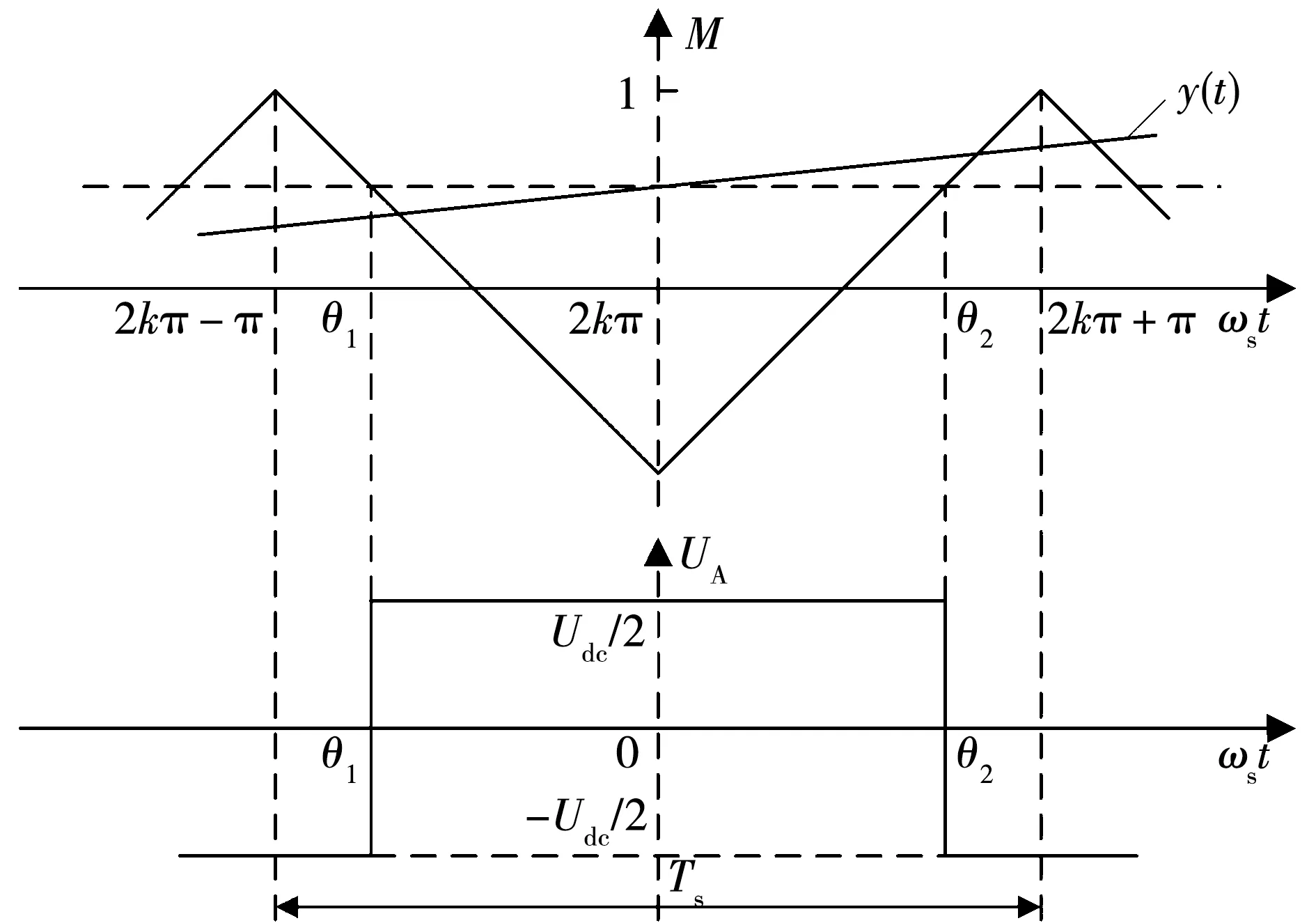
图1 SVPWM对称规则采样Fig.1 Symmetrical regular sampled in SVPWM

isideband_1(t)≈i1_2cos(fc±2f0)t+i1_4cos(fc±4f0)t。

(1)

式中i1_2和i1_4为边带电流谐波分量的幅值。

对于径向磁通电机,作用于定子齿面上的电磁激励力是引起电机振动及辐射噪声的主要原因。由SVPWM所引入的边带电流谐波会使气隙磁场感应产生分布于载波频率及其整数倍频带范围的边带磁场分量,进而产生相应频带的边带电磁力。通常,气隙电磁力可以分为径向分量与切向分量,他们具有相同的时间与空间特征,通过Maxwell应力张量法,气隙处的电磁力可以表示为

(2)

式中:μ0为真空磁导率;Bn和Bt分别代表气隙磁密的径向与切向分量,而切向分量的幅值远小于径向分量,通常予以省略。

忽略磁饱和效应并考虑磁场叠加原理,径向气隙磁密Bn可以分解为定子电枢磁场Barm和转子永磁体磁场Bmag,即

Bn(θ,t)=Barm(θ,t)+Bmag(θ,t)。

(3)

式中电枢磁场可以被视为基波磁场B0与谐波磁场Bh的叠加,Bmag和Barm的表达式[8]为:

(4)

(5)

式中:μ为永磁体磁场阶次,考虑到永磁体基波磁场是振动噪声的主要贡献量,μ取值为1;v表示电枢磁的谐波次数;θ为空间机械角度;f0为电信号基波频率;fh为谐波电流频率;Nt为单元电机,数值上取电机极对数p与槽数z的最大公约数。

将式(3)～式(5)代入式(2)中,可以得到径向电磁力密度的解析表达式,其中,全部表达式有12项成分。为了简化体现出边带谐波分量,只考虑永磁体边带谐波与电枢谐波磁场的相互作用,具体表示[8]为

(6)

由式(6)可以看出,边带电磁分量与机械响应之间的多物理场解析模型可以通过时空特征的耦合关系建立。本文以时间频率特征为识别对象,在机械响应中的频率特征为fh±f0次,结合第一载波频率附近的边带电流谐波特征频率,fc±2f0和fc±4f0次,边带径向电磁力的主要阶次为fc±f0,fc±3f0和fc±5f0次。由上,常规SVPWM技术所引入的边带谐波成分及径向电磁力特征解析模型被完整建立。

1.2 边带电流谐波与声振响应特征识别

为了识别常规SVPWM边带电流谐波与声振响应频谱特征,本文采用由电机样机、测试平台、控制与测试系统组成的样机实验平台。电机样机选用一款小型电动汽车后桥驱动12槽/10极永磁同步电机,具体参数如表1所示。实验中的测试平台基于20 N·m磁粉测功机实现转矩加载,如图2所示。

表1 永磁同步电机样机参数Table 1 Key parameters of the prototype PMSM

图2 样机实验与测试平台Fig.2 Experimental setup with instrumentation

直流电源采用20 kW电池模拟器输出311 V-4 kW,驱动电路与三相全桥功率模块选用Infineon-BSM-75GB120DN2。本文所提出的PWM策略模型均在MATLAB/Simulink中建立,并基于dSPACE1103半实物仿真平台及其实时监控上位机系统,实现PWM信号输出、电流与位置信号的反馈、策略切换与参数实时更替。

在测量相电流、壳体振动与辐射噪声信号时,本文将ICP型三向加速度传感器安装在电机冷却壳体上,传感器灵敏度为42.32 mV/g;参考了声学测试标准,ICP麦克风测点的布置结合了电机结构参数,采用5个麦克风测点的半球面测试方法;振动噪声信号使用朗德SQuadriga II数据采集仪进行采集与运算;电流传感器选用霍尔电流钳,相电流信号使用YOKOGAWA ScopeCorder采集。

诸多参考文献中指出[8,14],边带谐波成分产生机理的本质为频率调制过程,相比于幅值调制与相位调制,边带谐波成分的幅值变化取决于电机运行速度而不是转矩负载状态。为了清楚地验证边带电流谐波与其相关的振动噪声响应,本文将样机的运行条件设置为1 000 r/min和4 N·m的高效率稳态工况区间,其中电机转速频率fr为16.67 Hz,电流基波频率f0为83.34 Hz。

边带电流谐波通过功率谱密度(power spectral density,PSD)方法进行处理,如图3所示,边带谐波成分在载波频率附近出现明显的阶次分布,特征频率为7 667 Hz(fc-4f0)、7 833 Hz(fc-2f0)、8 167 Hz (fc+2f0)和8 334 Hz(fc+4f0),验证了式(1)中的解析模型。此外,边带电流谐波的峰值出现在fc±2f0,幅值为-27.68 dB/Hz;fc±4f0的谐波幅值相对较低,幅值为-39.12 dB/Hz。

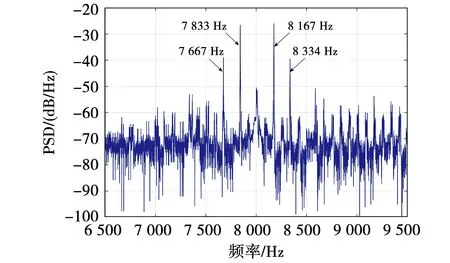
图3 常规SVPWM相电流波形与边带电流谐波成分Fig.3 Phase current wave and sideband current harmonic components in conventional SVPWM

边带声振响应频谱结果如图4所示,其中,图4(b)中的噪声频谱为5个麦克风数据均方根处理的结果,并且为了计算动态声压级,所选数据经过A计权(SPL-A)处理。类似于边带电流谐波,声振响应频谱中可以明显地看出阶次分布,特征频率分别为7 583 Hz(fc-5f0)、7 750 Hz(fc-3f0)、7 917 Hz(fc-f0)、8 084 Hz(fc+f0)、8 250 Hz(fc+3f0)和8 416 Hz(fc+5f0),再次验证了声振响应与边带电流谐波成分的相关性。声振响应的峰值出现在fc-3f0次处,幅值分别为0.175 m/s2及53.76 dBA。

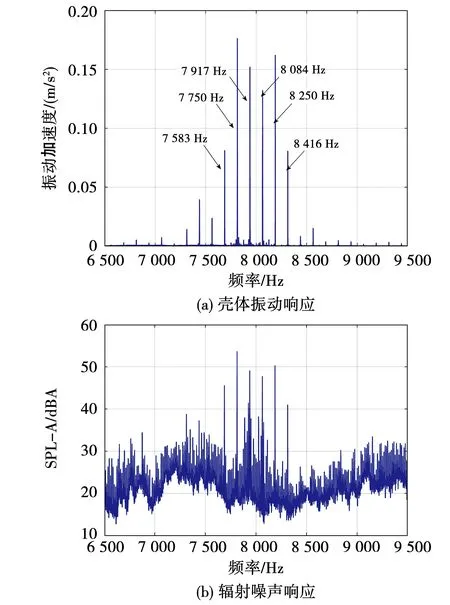
图4 常规SVPWM边带成分声振响应Fig.4 Sideband vibro-acoustics in conventional SVPWM

2 Markov链随机脉宽调制技术

基于谐波扩频调制技术中的RPWM,即通过将原本固定的载波频率按照随机形式变化,使得相对集中的边带谐波成分转化为分布在指定频谱范围内的离散谐波成分,谐波能量随之降低,从而达到改善边带声振响应的效果。然而,RPWM依然存在随机数短时间内分布不均匀的问题,导致相电流脉动成分及开关损耗增大等问题。因此,本文引入多状态Markov链模型,优化生成随机数效果,并应用粒子群算法选择最优的转移概率与随机增益。

2.1 RPWM技术原理与随机数分析

RPWM技术的核心是随机数生成策略,考虑到硬件设备生成随机数的难易程度,通常采用伪随机数生成方法[18]。原本固定载波频率fc随机化后的随机载波频率fn+1可以表示为

fn+1=fc+Rs。

(7)

式中:s为[-1,1]区间范围内的任意数值;R为伪随机数生成策略的随机增益,在频谱中的具体体现为边带谐波成分的扩频宽度。

由上式可以看出,随机化后的调制效果由某时刻的随机数值s和随机增益R共同决定,即载波频率变化范围为[fc-R,fc+R]。为了反映出脉冲宽度随机化程度,图5给出了基于非对称规则PWM采样的RPWM信号示意图,需要说明的是无论对称还是非对称规则采样PWM策略,其随机化前后对于载波频率附近的边带谐波及其边带声振响应的影响是相当有限的。此外,常规RPWM的随机载波频率生成结果如图6所示,由于RPWM对随机数生成并未加以限制,因此在随机数生成过程中会无法避免地产生某时间段内随机数值大于或小于平均期望值,其所影响的随机载波频率也会在某段时间内大于或小于中心载波频率。

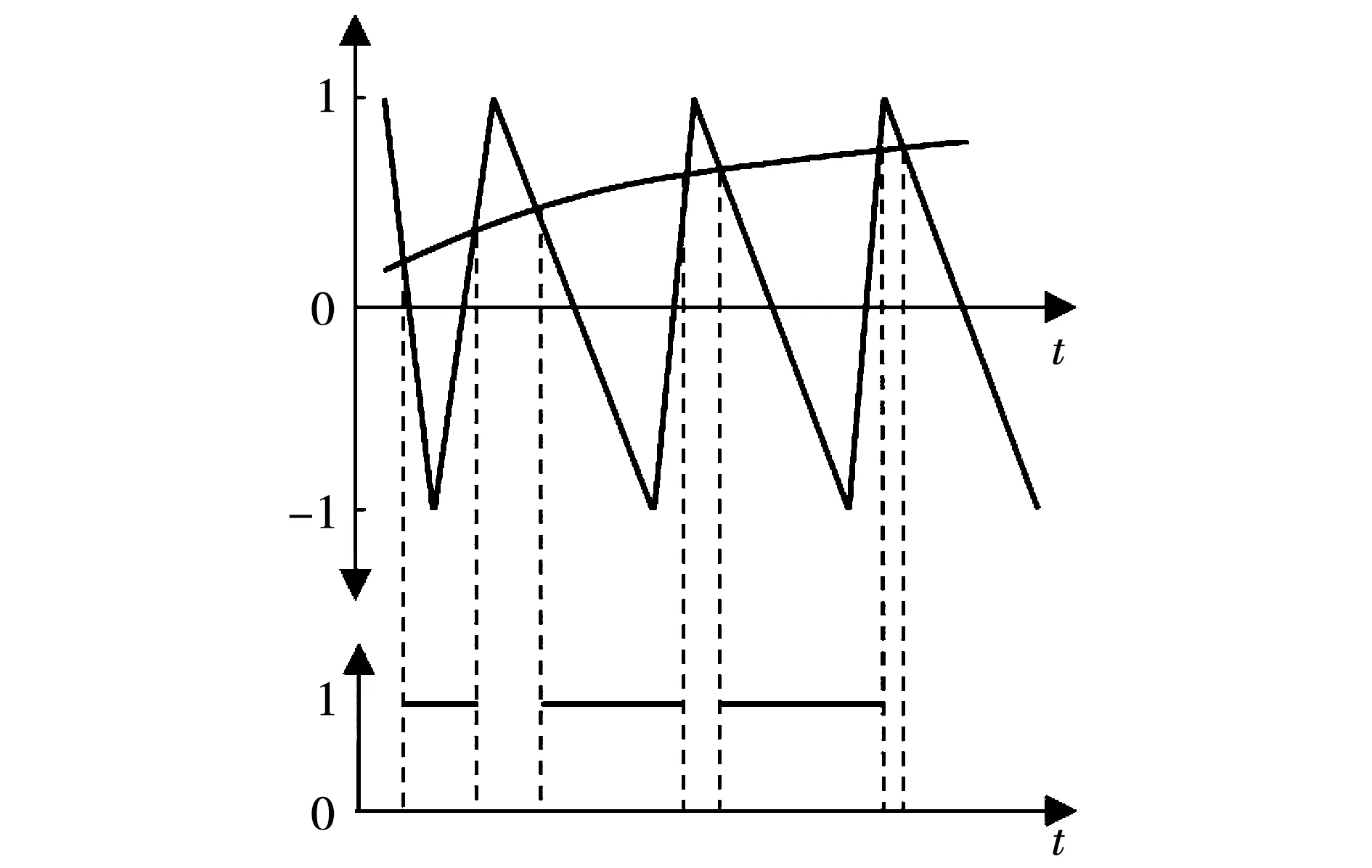
图5 随机载波频率PWM示意图Fig.5 Schematic diagram of random PWM

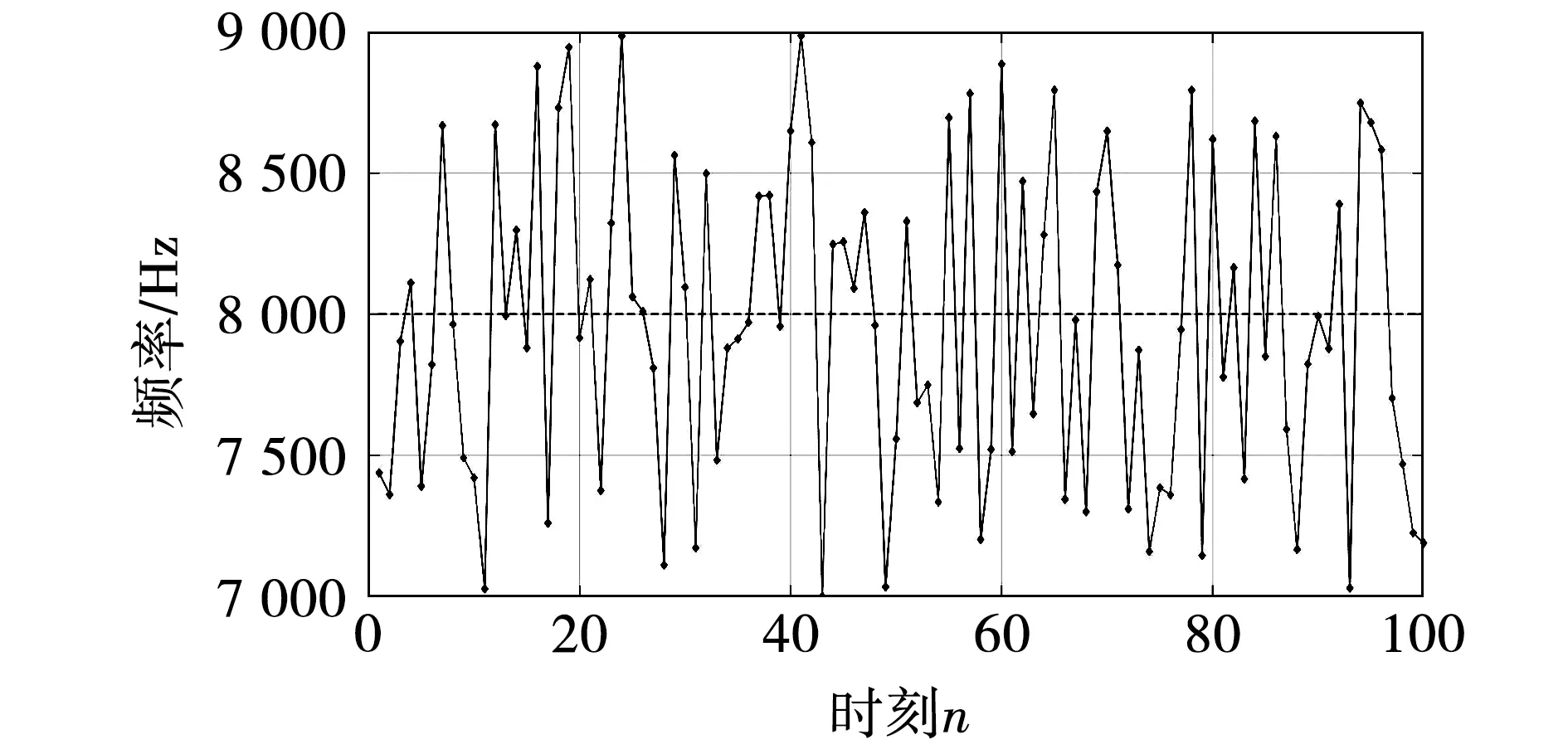
图6 常规RPWM的随机载波频率生成结果Fig.6 Simulation results of carrier frequency in conventional RPWM

2.2 Markov链原理与多状态随机数产生过程

Markov过程被称为无后效过程,即随机事件序列下一时刻的取值(an+1,tn+1)只与当前时刻的取值(an,tn) 有关,与之前的取值无关[19]。在随机优化算法仿真与实际设计中,需要将连续事件进行离散化,形成离散Markov链,因此本文引入单一时刻的条件转移概率Pij(m,n),具体表示为

Pij(m,n)=P{Xn=aj|Xm=ai}=

P{Xn=j|Xm=i),i,j∈S。

(8)

式中S为状态空间,S={a1,a2,…,an}。转移概率Pij(m,n)的意义为:m时刻系统处于状态ai,经(n-m)时刻后转移到状态aj的条件概率;亦可以理解为系统m时刻状态i,转移到n时刻状态j的概率。

随着状态空间数量的增加,转移矩阵所含元素越多,这也意味着优化后的随机数效果更加理想。为了避免状态空间数量所引入额外计算量,本文将未知参量控制在10个以内。

两状态Markov链随机载波频率系统设计是将原先载波频率的变化区间[fc-R,fc+R]分解为[fc-R,fc]和[fc,fc+R]上下两个部分,从而构成载波频率的状态1和状态2空间。如设状态1的概率为pa,状态2的概率为pb,构成的两状态转移概率矩阵为

(9)

式中pa和pb的取值为(0,1),且pa+pb=1。

三状态Markov链随机载波频率系统的设计是在两状态的基础上,将载波频率的变化区间进一步细分,引入调制系数k,k∈(0,0.33),载波频率变化区间被平均分割为[fc-R,fc-kR]、(fc-kR,fc+kR)和[fc+kR,fc+R]三部分,分别对应状态1、状态2和状态3。每个状态所对应的概率分别为pa、pb和pc。考虑到矩阵中每行每列之和为1,所构成的三状态转移概率矩阵可被进一步简化,即

(10)

式中p1和p2的取值为(0,1),且p1+p2=1。

多状态Markov链随机载波频率生成结果如图7所示,与常规RPWM的随机载波频率生成结果相比,随机数分布更加均匀,随机频率的分布得到了很好的优化。两状态Markov链的随机化载波频率的分布仍然有部分时刻大于或小于平均期望值;随着转移概率矩阵的增加,三状态Markov链的随机数性能进一步提高,随机化载波频率分布更加均匀。

2.3 基于粒子群算法的随机参数寻优

从上述分析中可以看出,随机增益R与转移概率P对边带谐波抑制效果的影响较大,而且这两个参数在系统参数设计中需要限定取值范围,避免占用主控芯片较大的计算内存。因此,本文选用粒子群算法,对R和P参数进行快速寻优,从而达到最优的边带声振抑制效果。

粒子群算法(particle swarm optimization,PSO)属于群智能算法,是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的元启发式优化算法[20],相比于传统常用的模拟退火算法(simulated annealing, SA)和遗传算法(genetic algorithm,GA),PSO不需要对初始粒子进行种群交叉与变异,仅通过内部迭代即可实现对最优目标解的求解,并且凭借其全局高精度收敛及鲁棒可靠性等优点,在多目标优化、自适应控制、非线性和多维度空间寻优等领域得到了广泛应用[21]。

PSO算法作为随机搜索算法,其核心驱动因素是将全局历史最优解Gbest与个体历史最优解Pbest进行共享更新迭代,从而实现个体极值与粒子群全局的最优求解,具体流程如图8所示。

全局最优解Gbest的筛选求解过程如下:

1)系统初始标定:根据实验采集到的相电流数据,标定仿真模型d轴电感、绕组电阻等参数,确保仿真模型各工况下与实验结果相符。

2)限定粒子初始位置与极值:R的范围设定为1 000～2 000 Hz,P的范围为0.5～1。

3)初始化粒子群:粒子群中的每个粒子包含2个基本信息,随机增益R和转移概率P,在每次迭代过程中,每个粒子的最优解Pbest将会与全局最优解Gbest进行比较和更新。考虑到变量个数较少,本文设定粒子群个数为20个。

4)运行稳态工况Simulink仿真程序,并在MATLAB工作区间生成相电流时域波形数据库。R的计算步长为每步100 Hz;P的计算步长为每步0.01;将生成的500个数据文件整理为数据库,再由PSD程序对数据进行时频转换;由于实际频谱中两端幅值较低,对PSO算法的收敛过程存在干扰,故将频带范围修正为7 750～8 250 Hz的频谱范围,最终拾取个体最优值Pbest和全局最优值Gbest。

5)边带电流谐波的最小值修正与判定:将修正后频带范围内的值共同减去一个特定值(40 dBA)形成中间数据库,再将中间数据库取负数,选取其中的最大值判定为Pbest,并更新Gbest。

6)终止条件设定:标准PSO算法中终止条件通常为迭代步数和收敛判据。为了保证群体的多样性或单一性,本文将迭代步数作为终止条件,以防止粒子群早熟收敛或过度迭代不收敛。

3 实验结果

3.1 RPWM边带电流谐波与声振响应

RPWM边带电流谐波成分如图9所示,基于RPWM边带电流谐波的阶次分布得到了有效地抑制,谐波幅值抑制到-40 dB/Hz以下。此外,由于随机数性能的非理想因素,边带谐波的峰值略偏小于8 000 Hz。

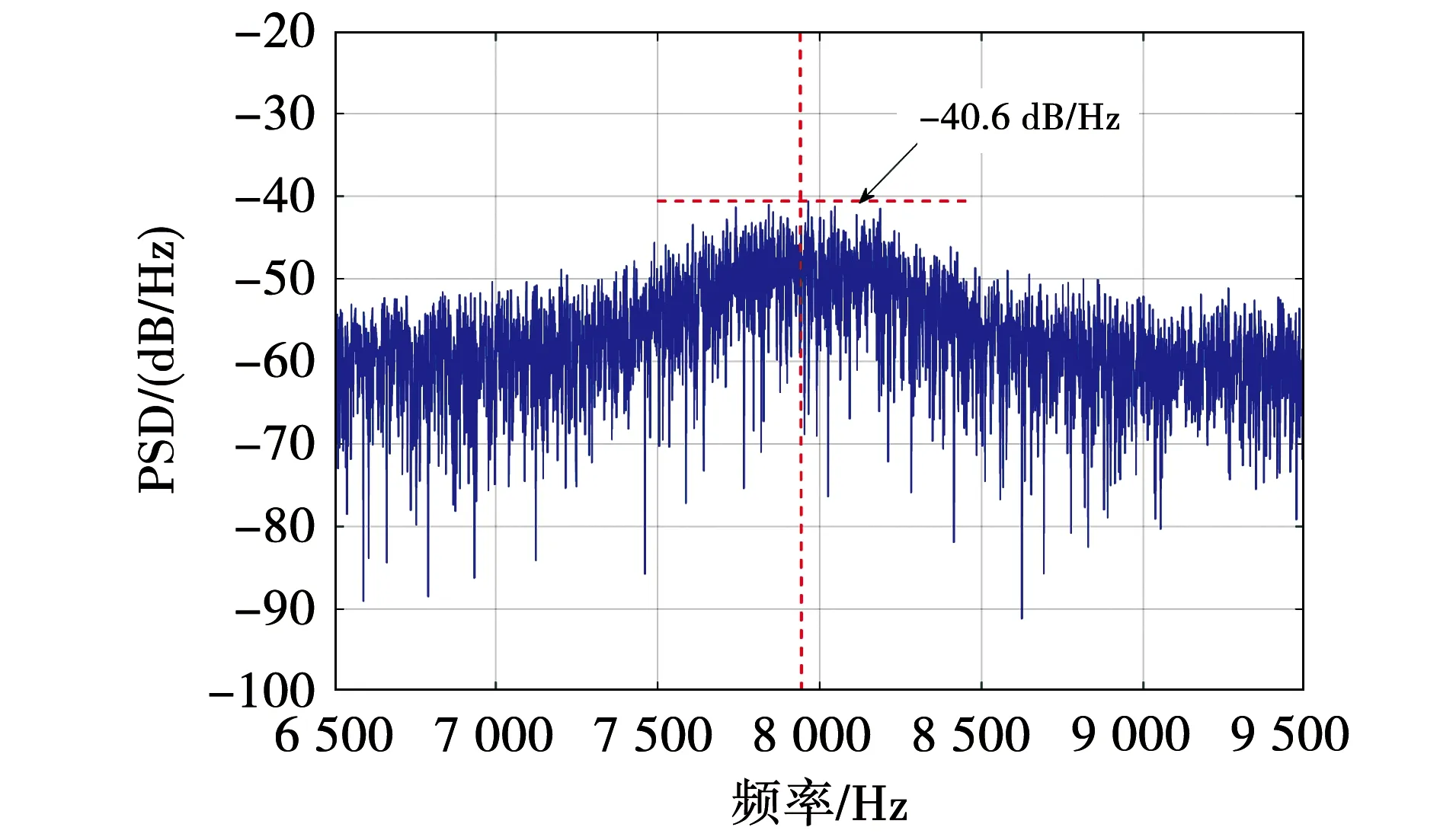
图9 RPWM边带电流谐波成分Fig.9 Sideband current harmonic components in RPWM

声振响应频谱如图10所示,与边带电流谐波类似,边带声振响应中明显的阶次效应得到了显著的抑制,其中振动幅值抑制到0.06 m/s2以下,A计权声压级幅值抑制到45 dBA以下。RPWM的边带电流谐波与声振响应呈现出明显的相关性,并且同时表现出不对称性,峰值均分布在小于中心频率8 000 Hz的一侧。

由于RPWM的本质仍然是频率调制,即边带电流谐波和振动声响应的大小与速度条件正相关,而对负载条件的变化不敏感,因此图11进一步给出了4 N·m恒定转矩下不同转速工况的噪声频谱实验结果,可以看出,边带声压级频谱分布仍显示出不均衡性。

3.2 多状态Markov随机载波频率调制实验结果

为了能够优化随机数性能,本文基于PSO优化算法对其中的关键参数进行了快速寻优;基于最优的随机参数,引入多状态Markov链随机脉宽调制改善随机载波频率分布,进一步抑制边带声振响应,以满足最优的边带谐波成分及声振响应抑制效果。

基于PSO算法的随机参数寻优结果如图12所示,在迭代过程中最大迭代步数步长设置为60,目标函数的误差值在40个迭代步数内趋于稳定,即边带电流谐波的抑制效果达到最优。此时,转移概率P的值等于0.68;随着随机增益R值的增加,边带谐波峰值减小,且在R=2 000时达到最优效果;同时,图12(c)表明当R值大于2 000 Hz之后,对边带谐波及声振响应的抑制效果趋于饱和。

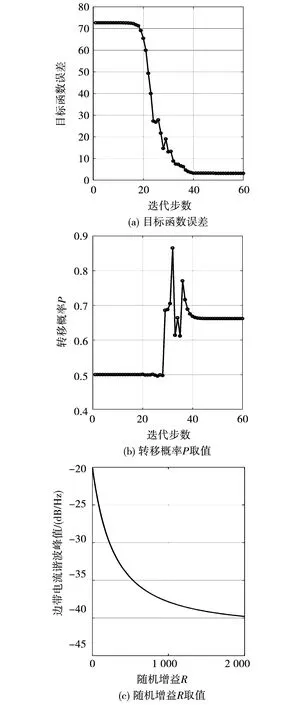
图12 基于粒子群算法的随机参数寻优结果Fig.12 Results of randomized parameters with PSO algorithm

根据上述的随机参数寻优分析,图13给出了参数最优下的多状态Markov链边带电流谐波抑制效果。从实验数据中可以看出,两状态Markov链的边带电流谐波峰值下降到了-40 dB/Hz以下,三状态Markov链的优化效果更为明显,抑制效果甚至达到了-50 dB/Hz以下;此外,相对于常规RPWM,多状态Markov链优化算法能够较好地改善边带谐波成分的频谱分布。

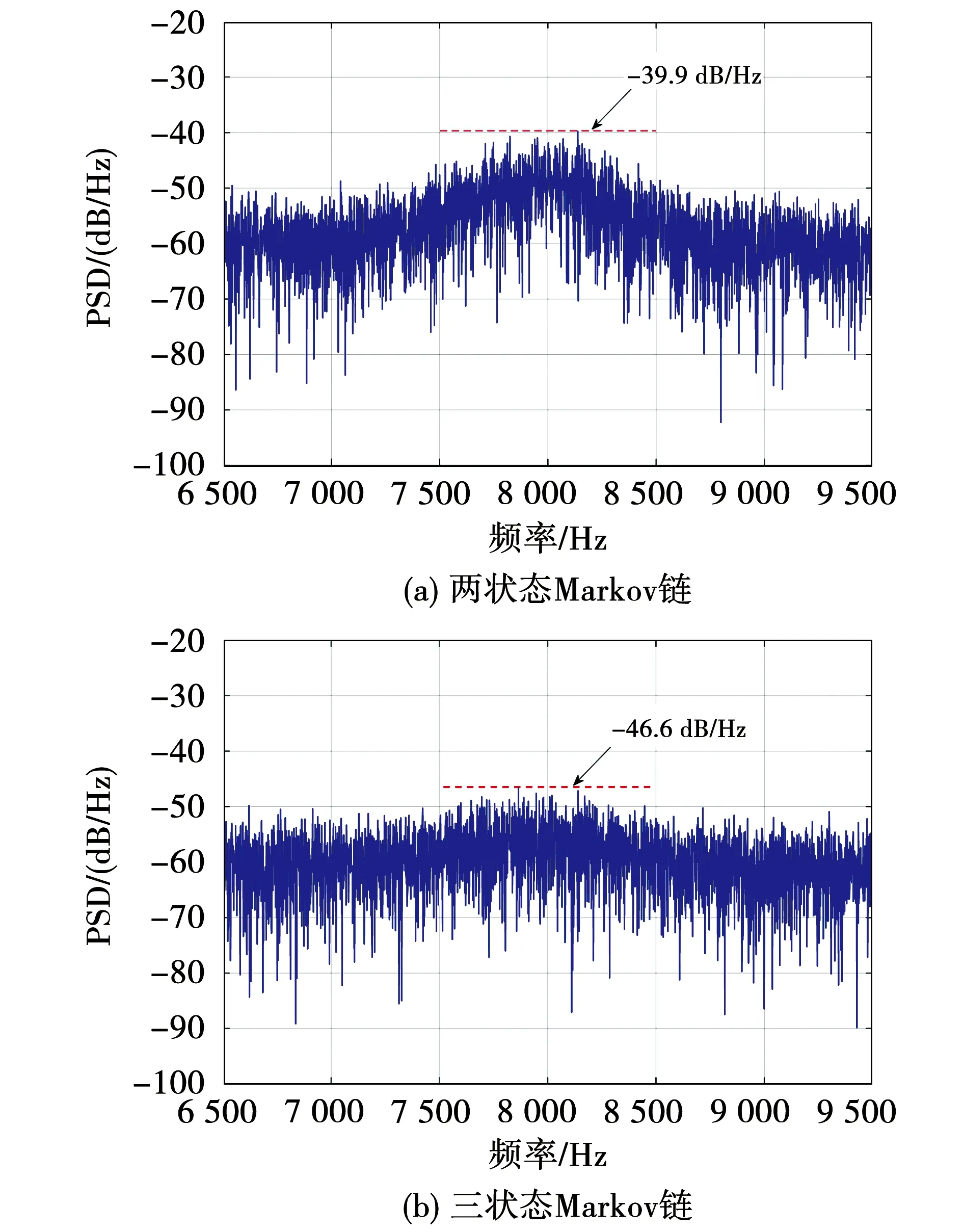
图13 多状态Markov边带电流谐波抑制效果Fig.13 Suppression of sideband current harmonic components with muti-states Markov-chain

图14和图15分别给出了基于最优随机参数的多状态Markov链边带声振响应,抑制效果得到了进一步提升,两状态Markov链的边带声振响应峰值分别被抑制到了0.025 m/s2和40 dBA以下,三状态Markov链的边带声振响应峰值得到进一步抑制,分别为0.02 m/s2和35 dBA以下;相比于常规RPWM,引入多状态Markov链的频谱分布更加均匀且对称。

图16给出了不同转速工况的多状态Markov链全频带声学响应对比结果,相比于RPWM实验结果,边带噪声频谱分布更加均匀;三状态Markov的优化效果最优,高频段噪声幅值进一步下降,进一步验证了多状态Markov链策略的有效性。

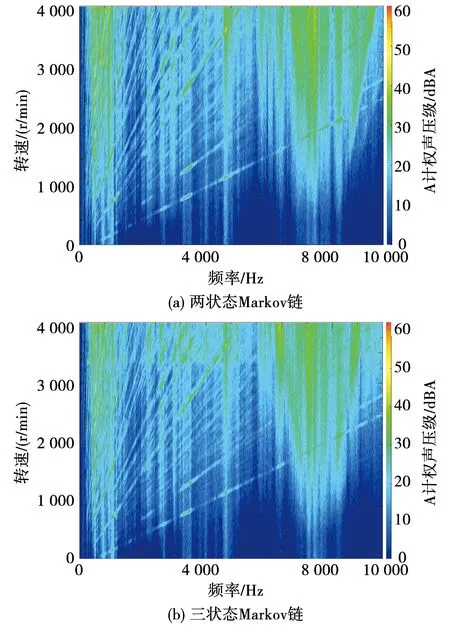
图16 不同转速工况的多状态Markov链全频带声学 响应结果Fig.16 Acoustic responses of multi-state Markov chain in full frequency band under with different speed conditions

4 结 论

为了抑制SVPWM所引入的边带电流谐波及声振响应,改善RPWM边带谐波成分的抑制效果,本文提出了基于多状态Markov链的随机脉宽调制方法,并利用PSO算法对其关键随机参数进行寻优。结合样机实验验证结果,所得出的结论如下:

1)RPWM可以有效抑制边带电流谐波,在声振响应中也呈现出明显的优化效果,然而,由于RPWM的随机数生成性能较差,优化后的边带频谱分布偏小于中心频率。

2)多状态Markov链随机脉宽调制可以有效优化随机数性能,进一步优化了边带电流谐波及声振响应,并且边带频谱的分布呈现出较好的对称性与均匀性;最优噪声抑制效果可以达到15 dBA以上。

3)所提出的PSO优化算法可以有效对随机增益R与转移概率P进行寻优;此外,本文所研究的内容可以面向PWM供电的电驱动系统,为后续永磁同步电机控制系统效率、转矩脉动、电磁干扰等研究提供理论与实验依据。