基于改进布谷鸟算法的微电网源-荷-储功率优化调度

何玉灵，解 奎，孙 凯，焦凌钰，王海朋,2，杜晓东,4，吴学伟

（1.华北电力大学 能源动力与机械工程学院，河北 保定 071003；2.电力机械装备先进制造与智能运维河北省工程研究中心，河北 保定 071003；3.华北电力大学苏州研究院，江苏 苏州 215123；4.国网河北电力有限公司 电力科学研究院，河北 石家庄 050000）

0 引言

微电网是由分布式电源、负荷、配电设施、监控和保护装置等组成的小型发配用系统，其中分布式电源与智能化技术的快速发展是构建微电网的重要基础[1]。相比于传统电力系统，大量分布式电源、储能与新型负荷的接入使电力系统出现供电多元化、用电互动化、电力电子化、装备智能化以及管理数字化等全新形态特征。因此，适应新型微电网的调度方式与运行控制策略具有重要的研究价值[2]。

在微电网经济优化调度研究方面，国内外学者已开展了大量的研究工作，并取得了一定的研究成果。文献[3-5]综合考虑微电网运行的经济性和环保性等影响因素，建立了以运行成本最低和环境影响最小为目标函数的优化模型；文献[6]构建了具有相关经济成本和环境效益的微电网系统优化规划问题的多目标函数，并提出了一种改进的阿基米德优化算法（IAOA）来获取全局最优解；文献[7]提出一种基于需求响应和边缘计算的多实体配电网分布式优化调度方法，通过分别建立所有者和产消者的最优模型，利用控制中心和边缘节点的协同作用实现配电网分布式优化；文献[8]在微电网中通过考虑需求响应的方式优化用户用电模式，改善负荷曲线、实现系统稳定运行；文献[9]提出了一种新的考虑负荷减少问题的微电网最优调度模型，该模型确定了微电网局部发电机的最优调度，以使相关配电系统的发电成本最小化；文献[10]研究需求响应的分时电价策略，通过各时段不同的激励方式实现负荷特性的改善；文献[11]为了解决用户用电成本的最优运行问题，提出了一种最小化用户电费和用户用电运行成本的最优运行模型，并以多种类型的家庭负载的调度弹性为对象，将其量化为考虑分时电价的需求响应；文献[12]通过调度可转移负荷与可削减负荷达到了降低系统运行成本及削峰填谷的作用；文献[13]基于模糊数学理论，以最小化微电网的总经济成本和网络损失为目标，将不可控的微源视为负载，提出了一种具有相关约束条件的模糊多目标优化模型；文献[14]针对孤岛模式下的微网经济运行问题，提出考虑储能装置能量状态的优化调度方法，并引入负荷竞价策略，将负荷响应作为辅助调节手段；文献[15]利用固定比例模型避免极端情况下负荷响应的不平衡，并通过基于电力估值的自主报价，避免了由于不同类型的用户具有不同的价格敏感性所导致的争议。

微电网优化运行不仅要考虑经济性，还要考虑电网调度对新能源消纳、微电网稳定性等方面造成的影响。文献[16]为提高微电网中可再生能源的消纳比例，提出了微电网点对点能源交易模型及反馈度量方法；文献[17]为提高直流微电网的稳定性，提出了一种分布式最优控制算法，以实时最小化运行损失（转换器损失和分布损失）为优化目标，将所有总线电压保持在预定义的范围内；文献[18]针对微电网处于并网状态或孤岛状态，设计包含风储的微电网运行架构，结合不同工况下的电能供需关系，建立了考虑用户满意度的多目标优化模型；文献[19]提出了一种有效利用可再生能源实现调峰填谷的分类定价策略，该策略根据用户端的需求和满意度对不同类型的负荷设置不同的电价，动态电价又激励用户调度可移动负荷并影响满意度；文献[20]综合考虑经济性、安全性以及用户舒适度，提出一种基于条件风险价值的孤岛型微电网动态激励调度策略；文献[21]为实现微电网运行过程中碳排放减少的目标，在微网优化的目标函数中引入碳交易成本，建立了一种碳交易机制下考虑柔性负荷的微电网低碳经济调度模型。

本文在以上研究的基础上，以微电网运行经济性和考虑碳排放的环境性为优化目标，引入考虑负荷调度补偿的用户用电满意度作为约束条件，采用负荷响应与储能作用为调度手段，实现微电网经济、环保的多目标优化，并防止负荷响应措施过于激进从而影响用户用电体验。建立了含风/光/储的微电网多场景优化配置模型，在考虑微电网寿命约束条件下，利用改进后的布谷鸟搜索算法（CS）求解微电网的最优调度策略。在4个典型场景中通过算例验证所提出的模型与算法的有效性，并探究负荷响应与储能对微电网的削峰填谷能力和经济性的影响。

1 微电网运行模型

微电网主要包括分布式发电单元、储能单元和负荷单元3 个部分，并直接接于同一母线上。由于地理范围小、线路较短，本文在构建微电网调度模型中忽略功率传输损耗。微电网系统结构如图1 所示。

图1 微电网系统结构图Fig.1 Structure diagram of microgrid system

图2 CS 算法流程Fig.2 Flow of CS algorithm

1.1 风力发电模型

风力发电是利用风力带动叶片转动，与叶片连接的发电机输出电能，实现风能到电能的转变，输出功率如式（1）所示：

式中：Pwt为风机输出功率；ρ为空气的密度；R为风叶的旋转半径；v为风机叶片上最大线速度；Cp为风力转换电能系数。

1.2 光伏发电模型

光伏发电是基于半导体材料将光能转换为电能。影响发电量的关键因素为光照强度与半导体材料周围的温度，输出功率如式（2）所示：

式中：Ppv、L、Tpv分别为目标环境下光伏发电的输出功率、光照强度、温度；PSTC、LSTC、TSTC分别为标准测试环境下光伏发电的输出功率、光照强度、温度；kT为功率温度系数。

1.3 储能单元模型

微电网中各时段储能单元的能量是变化的，用荷电状态（SOC）值表示各时段蓄电池储存的功率，t时段的SOC 计算表达式如下：

式中：St为t时段蓄电池的SOC 值；Psb,t为储能系统（蓄电池）在第t时段的充放电功率，充电时取负值，放电时取正值；Eb为蓄电池额定容量；Δt为时段。

1.4 负荷模型

本文从负荷运行调度的角度将用户负荷分为3 类：固定负荷、可移负荷和可断负荷。固定负荷是指使用时间和功率比较固定、不能进行调度的负荷；可移负荷是指使用时间和功率可以根据需要平移到别的时段的负荷；可断负荷是指可以根据需要部分或全部中断的负荷。在微网优化调度方面，微电网通过调度可移负荷实现运营成本经济性优化。

微电网t时段的总负荷为固定负荷、可移负荷和可断负荷的总和，其表达式为：

式中：PL(t)为微电网中t时段的总负荷功率；PB(t)、PM(t)和PD(t)分别为t时段的固定负荷功率、可移负荷功率和可断负荷功率。

对于可移负荷，在负荷移动时既要考虑当前时段转入负荷量，还要考虑同一时段负荷的转出负荷量，某一时段可移负荷的表达式为：

式中：PM_in,i(t)为i时段移入t时段的可移负荷功率；PM_out(t)为t时段的可移出负荷功率。

2 微电网日前优化调度模型

2.1 目标函数

2.1.1 经济性目标函数

微电网的经济成本主要由各微电源发电、储能运行成本、微网与主网的交易成本及负荷响应补贴构成。微电网的经济成本可表示为：

式中：Cmg为微网经济成本；Cwt为风力发电成本；Cpv为光伏发电成本；Csb为蓄电池运行成本；Cgrid为微电网与主网交换电能成本；CD为用户中断用电补偿；CM为用户用电负荷调度补偿。

式中：αwt为单位风力发电成本；αpv为单位光伏发电成本；Rsout,t为t时段蓄电池状态，1 为蓄电池处于放电状态，0 为蓄电池处于不充不放状态；βsb为蓄电池单位放电成本；gB为t时段微网单位购电成本，售电时为0；gsell为t时段微网单位售电收益，购电时为0；Pgrid为微网与主网交互功率，微网购电时为正，微网售电时为负；λD为可断负荷补偿系数；at,i为负荷从i时段移到t时段的单位调度补偿。

式中：a1、a2、a3、a4分别为可移负荷移动不同时段的补偿系数。

2.1.2 环保性目标函数

本文将CO2排放量作为微电网环保性指标，其中微电网的碳排放量主要来自于主网火力发电。微电网运行时产生的环保成本为：

式中：Cmp为环境成本；e为碳排放成本系数；E为边际排放因子。

2.2 约束条件

优化调度模型的约束条件包括系统运行约束、蓄电池运行约束、用户满意度约束。

2.2.1 系统运行约束

1）功率平衡等式约束。

2）电网交互功率约束。

在并网运行状态下，日前负荷调度优化对电网交互功率的控制输出应满足线路容量限值以及主网对交互功率的限制，即

式中：Pgs,max为微电网向主网售电的功率上限，用正数表示；Pgb,max为电网从主网购电的功率上限，用正数表示。

3）调度负荷功率约束。

为满足用户基本用电需求，对负荷的调度功率进行限制，表达式为

式中：PM_out,max、PD,max分别为移出负荷功率上限和可断负荷功率上限。

2.2.2 蓄电池运行约束

1）蓄电池充放电约束。

蓄电池充放电功率约束条件如式（13）所示

式中：Psout,max为最大放电功率；Psin,max为最大充电功率。

蓄电池的充放电次数条件如式（14）所示。

式中：Rsin,t为t时段蓄电池状态，1 表示蓄电池处于充电状态，0 表示蓄电池为不充不放状态。

蓄电池不能放电的同时又充电，也不能充电的同时又放电，因此必须满足式（15）。

2）蓄电池状态约束。

式中：Smax、Smin分别为储能系统（蓄电池）的荷电状态（SOC）的上限和下限。

蓄电池的始末能量状态约束条件如式（17）所示。

式中：S0为储能系统（蓄电池）的初始荷电状态值；S24为储能系统（蓄电池）的末态荷电状态值。

2.2.3 用户满意度约束

当负荷响应时，可移负荷的调度会直接影响用户的用电习惯，而负荷调度对用户的影响可用用户满意度来衡量。用户满意度可分为2 部分：一是用户舒适度，二是用户经济度。本文根据用户用电的舒适度与经济度计算用户用电的满意度，计算公式如下[22]：

式中：M为用户满意度；Ucom为用户负荷优化后的用电舒适度；Ueco为用户用电负荷的经济度。

根据用户实际用电曲线和舒适度最大曲线的差异计算用户的舒适度，计算公式如下：

根据负荷优化前后用户用电的成本差异计算用户的经济度，计算公式如下：

式中：Cbef为负荷调度前用户用电成本；Caft为负荷调度后用户用电成本。若Ueco＞1，则负荷优化后用户的用电成本减少，其经济度优于负荷响应前；反之，若Ueco＜1，则其经济度不如响应前。故Ueco值越大，用户的经济效益越好，用户的满意度值越大。

3 基于改进布谷鸟搜索算法的模型求解方法

布谷鸟搜索（Cuckoo search algorithm，CS）算法是受自然界中布谷鸟寄生育雏习性的启发而提出的，是一种群体智能搜索技术，考虑了布谷鸟巢寄生性与莱维飞行（Levy flights）模式，通过随机游走更换鸟巢的位置，具有很强的全局搜索能力[23,24]。

3.1 考虑动态变化步长的CS 算法

布谷鸟搜索算法中的3 个基本假设：

1）假设布谷鸟每次产蛋只有一个卵，并随机选择鸟窝位置来孵化它；

2）在搜索新鸟巢的布谷鸟群中，占据最好位置的鸟能够在该鸟巢中产下下一代的蛋；

3）可以使用的鸟窝的数目是一个常数，现在假设寄主鸟发现布谷鸟蛋的概率为Pa，Pa∈[0,1]。假如布谷鸟寄生被发现，那么寄主鸟将在附近新建一个鸟窝。

全局搜索通过Lévy 飞行执行，莱维飞行位置更新公式如式（21）所示。

式中：xkj为第j(j=1,2,3,···,n)只鸟巢在第k代的位置；⊗为点对点乘法；α为步长控制量，用来控制步长大小。

其中

Lévy 飞行输出的随机数由正态分布生成的随机数列构成，步长通过Mantegna 算法进行计算，如式（23）所示。

其中μ和ν服从正态分布：

局部搜索通过局部随机游走执行，位置更新公式如式（27）所示。

式中：xmk和xnk为当代鸟巢中随机两个鸟巢的位置；H(μ)为赫维赛德函数；Pa为最大发现概率；s为移动步长；ε为均匀分布的随机数。

算法的步长决定算法搜索解的空间，一般情况下，布谷鸟搜索算法步长通常取α=1。固定的步长设置一定程度上限制了对解的搜索，在算法的运行初期，步长取较大值时可以扩大搜索空间，达到较好的全局搜索；当算法运行到较小空间时，缩短步长可以更有利于局部搜索，提高搜索精度；因此可通过使用动态变化的步长增强算法的搜索效率。

式中：a、b、c为步长控制量，且a＞b＞c；k为当前迭代次数；N为总迭代次数。

3.2 CS 算法的基本操作

在微电网的优化调度问题中，已明确各时段的原始负荷曲线和风机、光伏出力，但是每个时间段储能系统（蓄电池）的充放电状态与可移负荷调度情况并不确定。因此在微电网优化调度问题中，可通过计划24 个时段内负荷响应和蓄电池作用状态来进行电网优化规划。

使用布谷鸟搜索算法解决该问题时，一个鸟巢表示一组24个时段内蓄电池充放电状态与负荷响应状态，鸟巢位置的优劣表示微电网经济性的优劣，通过寻找位置最好的鸟巢获得微电网经济性优化调度方案。

算法应用步骤如下：

步骤1）初始化。确定目标函数f(x)，初始化鸟群，随机产生n个鸟窝的初始位置xj(j=1,···,n)。设置算法参数：鸟巢数量n、维度nd、发现概率Pa、最大迭代次数N等参数；

步骤2）按式（21）更新当代鸟窝的位置，计算该鸟巢位置的优劣，与上一代鸟窝的位置进行对比，保留位置较好的鸟窝；

步骤3）用随机数r作为鸟窝主人发现外来鸟蛋的可能性，将其与鸟被淘汰的概率Pa进行比较。若r＞Pa则随机改变鸟窝位置，得到一组新的鸟窝位置，并保留较好的鸟巢位置；

步骤4）判断当前迭代次数是否满足设置的最大迭代次数。若满足则结束搜索过程，输出全局最优值fmin与全局最优位置；否则，重复步骤2）进行迭代寻优。

4 算例分析

4.1 基础数据

本文选取某微电网作为研究对象，调度周期为1 天，划分为24 个时段进行优化调度。微电网运行模型包含实际微电网典型特征，运行期间分时电价、负荷调度补偿等参数符合现实电力政策。为响应双碳政策，新能源发电全消纳，该微网中风机、光伏出力时序曲线和原始负荷功率时序曲线如图3 所示。

图3 负荷功率与风机、光伏出力时序曲线Fig.3 Time series curve of load power and output of fan and photovoltaic

微网与主网间最大交换功率为90 kW，碳排放成本系数为0.4 元/kW·h，边际排放因子取1.1，风力发电与光伏发电容量上限分别取100 kW、50 kW，发电成本分别为0.52 元/kW·h、0.75 元/kW·h。各时段电价如表1 所示，负荷响应的约束与补偿系数见表2 与表3。储能系统（蓄电池）额定容量的大小是150 kW·h，荷电状态（SOC）变动限制是[0.3,0.95]，零时刻荷电状态值是0.4，放电成本为0.4 元/kW·h，调度日内充电和放电的次数要求皆小于或等于8 次，最大充放电功率为30 kW。

表1 分时电价Tab.1 Time-of-use electricity prices

表2 可移负荷响应合同Tab.2 Shiftable load response contract

表3 可断负荷响应合同Tab.3 Breakable load response contract

4.2 场景分析

本文基于工程实际中日前负荷、风机、光伏的预测数据，构建考虑负荷调度和储能作用的微电网协同规划模型，通过改进CS 算法得到经济性最好的电网功率调度方案，实现考虑环境成本下微电网运营成本降低与环保性提升。为验证文中所提规划方案的可行性，考虑以下4 种场景下微电网的日前优化调度：1）既不考虑负荷调度，又不考虑储能作用；2）只考虑负荷调度；3）只考虑储能作用；4）既考虑负荷调度，又考虑储能作用。

4.2.1 多场景对比

由表4 可知，当微电网运行既不考虑负荷调度，又不考虑储能作用时（场景1），用户未参与可移负荷响应，认定用户满意度为1。在此场景下微电网的运营成本为2 397.1 元。

表4 不同场景下的优化调度结果Tab.4 Optimal scheduling results in different scenarios

当微电网运行只考虑负荷调度时（场景2），在保证用户满意度不小于1 的前提下，微网的成本支出为2 101.5 元，与场景1 相比成本支出节省了12.33%，这是由于此场景通过调整部分用户的用电时间，将部分高电价时段的负荷移动到低电价时段，极大程度地减少微网的购电成本。负荷调度受用户满意度限制，牺牲用户满意度可以减少微网的运营成本，如满意度降低到0.98 或0.96时，微网成本支出减少到2 089.5 元或2 078.7 元。

当微电网运行只考虑储能作用（场景3），通过控制蓄电池的使用时间和功率，在用户满意度不小于1 的情况下，最大限度地提高微网的经济收益。与场景1 相比，此种调度场景下成本支出减少到2 145.6 元，相对减少了10.49%。

当综合考虑负荷调度和储能作用时（场景4），通过合理控制可移负荷和蓄电池实现经济性优化。在保证用户满意度都不小于1 的前提下，场景4 的成本支出相比于场景1 减少了13.02%。牺牲满意度可增强负荷响应的作用，随着满意度降低到0.98 或0.96，微网成本支出减少到2 074.0 元或2 069.3 元。

场景2 优化调度后成本减少了294.6 元，场景3 优化调度后成本减少了251.5 元，场景4 优化调度后成本减少了312.1 元。在经济性优化方面场景4 优于场景2，场景2 优于场景3，表明在此微电网模型中，可移负荷响应方案的经济性优于储能作用方案的经济性。同时协调负荷响应与储能作用能发挥更好的效果，相比于场景2 减少17.5 元，相比于场景3 减少60.6 元。

4.2.2 场景2 分析

图4、5 为调度前后场景2 下负荷响应优化调度结果与净负荷曲线。如图4 分析可知，在用电高峰17:00～22:00 时段内，可移负荷移动到2:00～7:00 时段，负荷功率峰值由145.2 kW 减少到124.08 kW；微网与主网间的电能交互可由图5中净负荷功率表示，优化后高峰时段17:00～22:00 净负荷功率峰值减少22.1 kW，高峰时段10:00～12:00内净负荷功率也有所降低，减缓了微网与主网间电能传输压力，微电网中可移负荷响应削峰效果良好。

图4 负荷响应优化调度结果Fig.4 Optimization scheduling results of load response

图5 负荷响应优化调度净负荷Fig.5 Optimization dispatching net load of load response

4.2.3 场景3 分析

图6、7 为储能作用优化调度结果和蓄电池荷电状态变化曲线。如图所示，在 2:00～3:00、4:00～6:00 时段微网风光发电和购电能够满足用电负荷的需求，此时段内系统中的储能容量较低，蓄电池处于充电状态，为后期的电能需求高峰期提供保障；在17:00～22:00 时段微网风光发电和购电无法满足用电负荷的需求时，通过蓄电池放电实现电能供需平衡，缓解微电网用电高峰时段的供电压力，保证微电网稳定运行。为延长蓄电池使用寿命，各时段蓄电池充放电功率均未超过30 kW。

图6 储能作用优化调度结果Fig.6 Optimization scheduling results ofenergy storage function

图7 蓄电池荷电状态变化图Fig.7 Change diagram of battery charging status

4.2.4 场景4 分析

如图8 所示，10:00～14:00 与17:00～22:00 时段内负荷移出，蓄电池处于放电状态；0:00～7:00与23:00～24:00 时段负荷移入，蓄电池处于充电状态。与场景2 相比，储能的加入使得高峰时段负荷移动减少，避免过度牺牲用户舒适度。图9 表明蓄电池在与负荷响应协调作用时荷电状态的变化。图10 显示负荷响应与储能作用前后，微网除风光发电外还需购得的电能资源，相较于优化前在用电高峰时段所需电能明显减少，微网用电高峰时稳定性显著增强。

图8 负荷与储能协调优化调度结果Fig.8 Optimal scheduling results of load and energy storage coordination

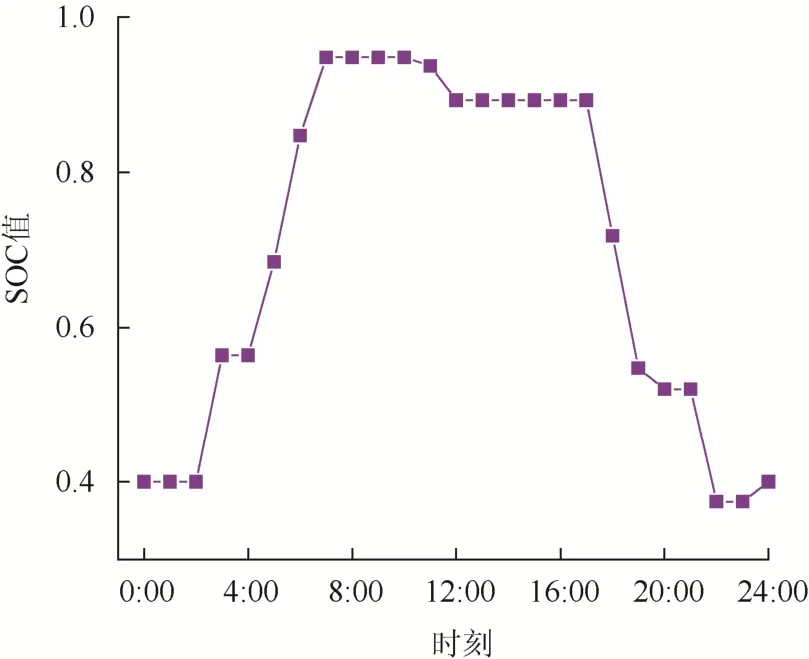
图9 蓄电池荷电状态变化图Fig.9 Change diagram of battery charging status

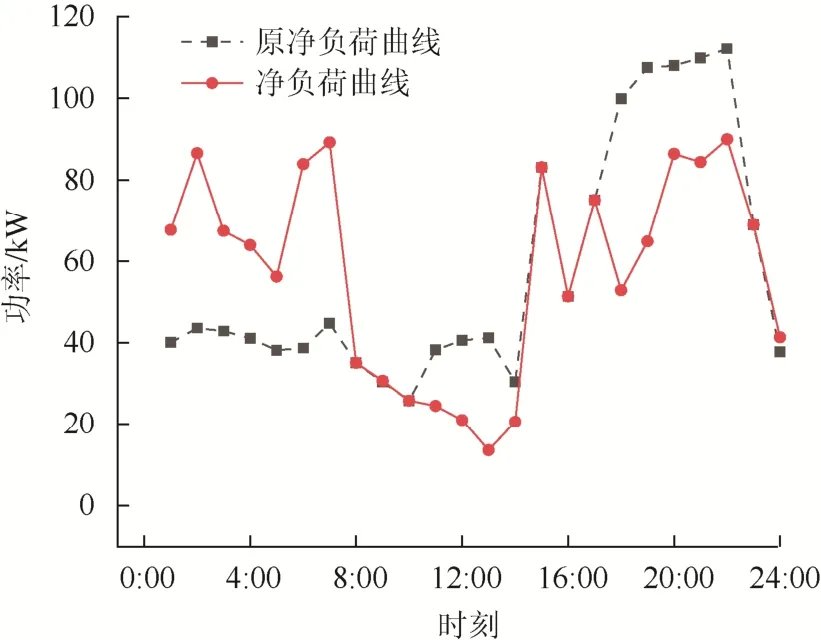
图10 负荷响应优化调度净负荷Fig.10 Optimization dispatching net load of load response

4.3 算法比较

为了验证改进布谷鸟算法的正确性和优越性，选择粒子群（PSO）算法和未改进布谷鸟算法求解场景2 的最优调度模型。微网运行成本、算法收敛性和计算时间如表5 所示。与其他两种算法相比，改进布谷鸟算法计算得到的成本支出最低。同时，在迭代次数相同的情况下，改进CS 算法的计算时间最短。3 种算法的迭代过程如图11 所示。结果表明，改进CS 算法在3 种算法中具有最快的收敛速度和最优解。

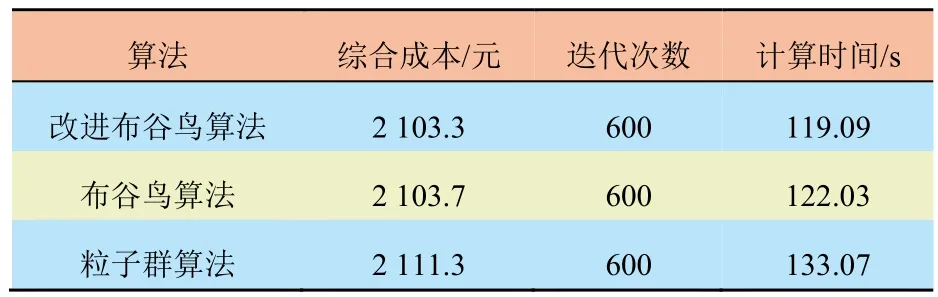
表5 算法比较结果Tab.5 Algorithm comparison result

图11 算法比较结果Fig.11 Algorithm comparison result

表6 给出了各算法中微电网电力成本的各个组成部分。由于风力发电机组和光伏发电的功率不变，因此3 种算法得到的风力发电机组和光伏发电的维护成本相同，而由于场景2 不考虑储能作用，储能的运行成本都为零。PSO 算法、CS 算法和改进的CS 算法得到的结果相近，但PSO 算法和CS 算法的计算时间比改进的CS 算法要长。此外，改进的CS 算法的收敛速度也比CS 算法快。结果表明，改进的CS 算法具有强大的优化能力和计算效率。

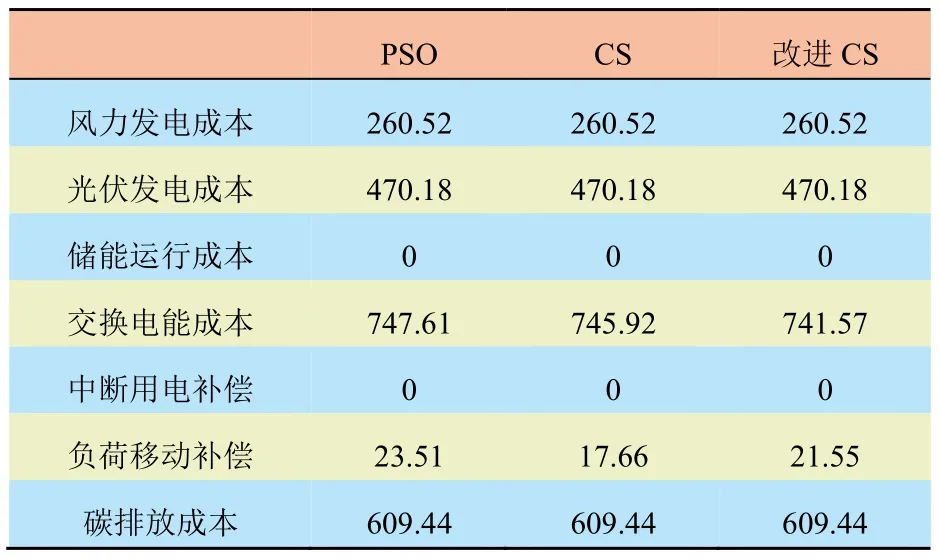
表6 成本构成分析Tab.6 Cost structure analysis 元

5 结论

本文提出了一种计及需求侧响应的微电网有功功率调度模型，实现在典型场景下微电网源网荷储的最优匹配，主要创新点如下：

1）以微电网调度经济性和环保性最优为目标，综合考虑了用户满意度和负荷等级；

2）基于自适应步长改进了布谷鸟优化算；

3）计算了4 种典型微电网场景，明确了需求响应和储能对微电网的影响。

通过对典型场景下微电网功率调度研究，具体可得以下结论：

1）通过多场景结果对比可知，在微电网经济优化方面，负荷平移的效果优于储能装置，两者综合的效果最佳。此外，与粒子群算法和布谷鸟算法相比，改进的布谷鸟算法在求解时间和求解精度方面的性能更优。

2）负荷调度可以有效降低微网运行成本，将部分可移负荷从高电价时段平移至低电价时段，在高峰时段有利于缓解微电网与主网进行电力交互压力，实现负荷削峰填谷。

3）用户满意度是限制用户参与需求侧响应的重要因素。满意度设置过高会导致用户参与需求侧响应受到的限制大；而满意度设置过低，则会损害用户参与需求侧响应的积极性。