基于改进TD3 算法的综合能源系统低碳经济调度

邱革非，何虹辉，刘铠铭，罗世杰，何 超，沈 赋

（昆明理工大学 电力工程学院，云南 昆明 650502）

0 引言

综合能源系统（Integrated energy system，IES）具有多能耦合的特性，在加快规划建设新型能源体系、推进能源绿色低碳转型的过程中起着重要作用。IES 运行的经济性与低碳性受到广泛关注。

针对IES 调度的经济性、低碳性问题，相关文献采用多种方法展开了研究工作。

针对IES 优化调度，文献[1]将并行计算与多维近似动态规划相结合；文献[2]采用了区间多目标线性规划方法；文献[3]采用了一种基于高斯回代的交替方向乘子法；文献[4]结合了信息间隙决策理论和模型预测控制。上述文献在研究中均采用了数学规划的方法，算法中包含较为复杂的数学推导和计算，所存在的问题是对应方法仅能处理特定问题。

文献[5]以系统和电动汽车运行成本最低为约束条件建立了双层优化模型。文献[6]在考虑碳捕集与电转气技术背景下建立了相关调度模型。以上文献在研究中采用了基于模型的方法，所存在的问题是所建模型的差异会导致优化结果存在误差，且对复杂系统的求解速度较慢，在有实时性要求的场景中模型通常无法满足要求。

文献[7，8]分别采用粒子群优化算法和改进非支配排序遗传算法求解相关调度问题，而文献[9]则对粒子群算法进行了改进。以上文献均采用了启发式算法。对比基于数学规划和模型的方法，这些方法有更好的可优化性、鲁棒性和适用性，但在处理非线性复杂问题时仍会受到限制，寻找全局最优解的难度较大，且无法自适应调整策略。

相较于上述几类方法，深度强化学习（Deep reinforcement learning，DRL）方法具有更强的适应性和泛化能力。对于具有序贯决策特点的问题，应用马尔科夫决策过程（Markov decision process，MDP）建模，能够更高效地寻找到最优解[10]。在将DRL 方法应用于电力系统调度方面：文献[11]将近端策略优化算法（Proximal policy optimization，PPO）应用于源荷不确定场景中。文献[12]采用的优势柔性演员评论家（Advantage learning loft actor-critic，ALSAC）算法，能处理有更大随机性的环境问题。以上采用了随机策略的方法在实际应用中通常有收敛速度较低、计算资源浪费、易产生不稳定结果的缺点。

文献[13]采用深度确定性策略梯度（Deep deterministic policy gradient，DDPG）对比随机策略方法，提高了计算效率与收敛速度，但也存在过估计、执行效率较低、动作探索能力弱、易陷入局部最优的问题[14-16]。文献[17]采用双延迟深度确定性策略梯度算法（Twin delayed deep deterministic policy gradient，TD3）解决电力系统运行的安全性问题，并在电力系统实际运行场景中体现出了方法的有效性与适用性；然而由其训练结果可知，该算法仍存在随机采样数据带来的收敛速度慢、需要大量迭代轮次的问题。

本文在现有研究基础上，通过对历史经验数据应用求和树（Summation tree）存储采样，实现优先经验回放，从而改进TD3 算法的训练效率与性能。具体过程为：对IES 的低碳经济调度策略优化作MDP 建模，建立决策交互环境以训练智能体决策能力。在训练过程中，基于数据更新价值对经验数据设置一优先级指标，以Summation tree存储采样，高效利用经验数据，提高训练效率。通过算例仿真验证了方法在IES 低碳经济调度中的有效性，并通过对比不同方法体现出训练效率和决策能力的提升。

1 IES 低碳经济调度模型

IES 系统结构如图1 所示。图中，IES 主要由光伏电源（Photovoltaic，PV）、风电机组（Wind turbine，WT）、燃气轮机（Gas turbine，GT）、用于回收热能的余热锅炉（Waste heat boiler，WHB）、直接生产热能的燃气锅炉（Gas boiler，GB）、电池储能系统（Battery energy storage system，BESS）以及电负荷和热负荷组成。此外，IES 还可与上级主电网购售电能，从外部天然气供应商购入天然气，并对系统内产生的污染物进行治理，以提高系统内能源利用率和系统运行的经济性、低碳性。

图1 综合能源系统结构Fig.1 Integrated energy system structure

1.1 IES 模型

1.1.1 光伏电源与风电机组

光伏电源实际出力与其所处环境中的光照强度和温度有关。风电机组出力则与风速有关。本文研究采用对应电源出力数据，即以PPV（t）和PWT（t）分别表示光伏电源和风电机组t时刻的输出功率。

1.1.2 燃气轮机与余热锅炉

燃气轮机与余热锅炉的发电、发热功率与所消耗天然气量关系为：

式中：GGT(t)、PGT(t)、QGT(t)、QWHB(t)分别为t时刻燃气轮机燃烧的天然气量、发电功率、发热功率以及余热锅炉发热功率；Hgas为天然气热值，取8.302 kW/m3；ηGT为燃气轮机电转化效率，取0.42；ηWHB为余热锅炉热转化效率，取0.85；ωGT为热损耗系数，取0.2。

1.1.3 燃气锅炉

当余热锅炉回收热能不足以供给热负荷时，启动燃气锅炉补充热负荷缺额。输入天然气量与输出发热功率关系为：

式中：QGB(t)、GGB(t)分别为t时刻燃气锅炉发热功率与所燃烧的天然气量；ηGB为燃气锅炉热转化效率取，0.84。

1.1.4 主电网

主电网与IES 进行能量交易的目的是，缓和分布式电源出力与负荷需求的不可控和间歇性问题，提高系统运行的经济性与稳定性。

主电网与IES 进行能量交易实施分时电价策略。

1.1.5 电池储能系统

电池储能系统将在分布式电源出力过剩以及储能系统未达最大允许容量时，对电能进行存储，并对其规模进行配置[18]。t时刻系统储能余量为：

式中：B(t)、B(t-1)分别为t、t-1 时刻的储能余量；ηcha、ηdis分别为储能系统充放电效率，分别取0.92、0.95；PB,cha(t)为t时刻充电功率；PB,dis(t)为t时刻放电功率。储能系统t时刻的荷电状态为：

式中：SC(t)为t时刻储能系统的荷电状态；Bmax为储能系统最大容量。

1.2 目标函数

在本文研究的IES 低碳经济调度问题中，通过协调控制系统内各设备出力与工作状态，在单位天然气燃烧产生的二氧化碳与其他污染物排放量一定的条件下，以系统内其他污染物排放量反映碳排放量大小，从而使系统以降低污染物治理成本、减少燃气轮机及燃气锅炉使用率的方式降低碳排放成本，达到低碳、经济运行目的。

系统总运行成本由购气成本、环境污染治理成本、系统运维成本以及与主电网的能量交易成本构成，目标函数可表示为：

式中：cgas为购气成本；cenv为环境污染治理成本；crun为运行维护成本；cmg为与主电网的能量交易成本。

燃气轮机和燃气锅炉2类设备的购气成本为：

式中：ξgas为气价，取定值。

此外，燃气轮机与燃气锅炉以及主电网内某些发电设备的运行将对环境造成一定影响，其所产生的环境污染治理成本为：

式中：ξeg为燃气轮机与燃气锅炉产生的环境污染治理成本系数；ξmg为主电网产生的污染治理折算后的成本系数；Pmg,b(t)为t时刻从主电网购入的电能。

运行成本主要考虑分布式电源与储能系统运行维护产生的成本，与设备实际出力大小有关：

式中：KWT、KPV、KB分别为风机、光伏、储能系统的运行维护成本系数。

燃气轮机与燃气锅炉仅考虑其运行时的购气成本，忽略其维护成本，其与主电网能量交易时的成本为：

式中：ξtou,b(t)、ξtou,s(t)分别为从主电网购入和向主电网售出电能的分时电价；Pmg,s(t)为t时刻向主电网售出的电能。

1.3 约束条件

系统运行受各设备运行约束条件以及电、热能量流的平衡约束。

1）电源出力约束。

式中：PPV,min、PWT,min、PGT,min分别为光伏、风机、燃气轮机的出力下限；PPV,max、PWT,max、PGT,max分别为光伏、风机、燃气轮机的出力上限。

根据燃气轮机运行特性，系统运行还需满足其功率爬坡约束：

式中：ΔPGT,max与ΔPGT,min分别为燃气轮机爬坡功率上下限。

2）电功率平衡约束。

式中：Le,i(t)为t时刻第i个电负荷功率；Ne为电负荷总数。

3）热功率平衡约束。

式中：Lh,j(t)为t时刻第j个热负荷功率；Nh为热负荷总数。

4）电储能系统约束。

5）考虑到主电网侧运行的稳定性问题，模型还需考虑满足与主电网的实时功率交互约束，即：

式中：Pmg,min、Pmg,max分别为综合能源系统与主电网交互功率下限和上限。

2 改进TD3 模型

2.1 IES 的MDP 模型

构成IES 低碳经济调度问题的MDP 模型要素，包括智能体在每个时刻t的状态空间集合s(t)、动作空间集合a(t)、以及与环境交互过程中在每个状态s(t)下由于采取对应策略下的动作a(t)而获得的奖励值r(t)。智能体可对主电网购售电、燃气轮机与燃气锅炉的出力、储能系统充放电进行调度，并在不断的训练中使调度策略趋于最优。

2.1.1 状态描述

在本文的研究中，1 个调度时段的长度为1 h，1 个调度周期为24 h。预设场景中，状态空间集合由分布式电源出力、电池储能系统荷电状态、电价信息以及2 类负荷需求量组成，故状态空间s(t)可表示为：

式中：PDG(t)为在每个时刻t下，光伏电源与风电机组设备的总输出功率。

2.1.2 动作描述

智能体在每个时刻t可对燃气轮机和燃气锅炉的出力、电池储能系统充放电、与主电网的购售电量进行调度，故动作空间a(t)可表示为：

式中：Ba(t)为电池储能系统充放电动作量。

燃气轮机由余热回收装置回收的热功率QWHB(t)出力由式（2）（3）根据PGT(t)折算，故不在动作空间组成成分中体现。

2.1.3 奖励值函数

IES 低碳经济调度问题以最小化系统总运行成本为优化目标，而智能体以最大化奖励值作为动作优化依据，故设定奖励值函数为对应目标函数取负。同时，为减少策略产生的功率不平衡现象，将设备出力导致的电、热功率不平衡作为罚函数附加至奖励值函数中：

式中：ci(t)分别对应每个调度时段t的购气成本、环境污染治理成本、运维成本、与主电网的能量交易成本；i=1,2,3,4；αi为对应成本的奖励值权重；g(t)为罚函数；βc、βg为奖励值函数与罚函数系数。

功率不平衡罚函数表示为：

式中：λP、λQ分别为电、热功率约束条件罚因子；εP(t)、εQ(t)分别为2 类约束的不平衡程度。

2.2 改进TD3 算法

TD3 算法是确定性策略方法DDPG 的一种优化改进方法[19]，其思路是：首先，为增强智能体动作探索能力并平滑更新参数时的策略期望值，在Actor 中分别添加行为策略噪声和目标策略噪声；其次为避免过估计现象，Critic 的现实网络和目标网络均采用双重网络；最后为提高输出策略的稳定性延迟更新Actor 现实网络参数，当Critic 网络更新多次后再对Actor 现实网络参数进行更新。

TD3 算法会在训练过程中对数据进行随机采样，这将导致训练效率偏低、奖励值收敛速度慢。Summation tree 作为计算机数据树形结构中的一种，其逻辑结构适用于TD3 算法对数据的存储、访问需求，应用于该算法中可提高数据处理效率。

本文将Summation tree 引入经验回放缓冲区中，为经验数据设置一优先级指标，以实现高效的优先经验回放、增加具有高更新价值经验数据的利用率、提高智能体训练效率，从而对现有TD3算法进行改进。

2.2.1 基于Summation tree 的数据存储采样

Summation tree 结构如图2 所示。图中，依数据添加顺序，在每个Summation tree 叶节点存储一条经验数据，并以数据的优先级指标作为该节点的节点值，父节点节点值为其子节点节点值之和。每次采样时，自根节点开始基于节点值大小，向叶节点寻找目标，寻找时总指向节点值较大的节点；添加新的经验数据时，从叶节点开始向根节点逐点更新节点值。

图2 Summation tree 结构Fig.2 Structure of Summation tree

由于时序差分（Temporal difference error，TD-error）较大的数据具有更大的梯度信号，因而有更大的更新价值，故可作为评估数据的更新价值即采样优先级的指标。

文中的Critic 网络采用动作-价值函数计算TD-error：

式中：γQ为折扣因子；Q(st,at)为动作-价值函数；st+1、st分别为t+1、t时刻对应状态；at+1、at分别为t+1、t时刻所采取的动作。

以每条经验数据的TD-error 作为其优先级指标，故可得数据的被采样优先级概率：

式中：ρl、δl分别为第l条经验数据的被采样优先级概率和对应的TD-error；υ为权衡因子。

υ=0 为均匀采样，υ=1 为贪婪策略采样。为减小δ较大数据与较小数据间被采样概率的差距，本文取υ=0.6。同时为避免采样不到TD-error 很小的经验数据，对新添加的经验数据作一初始化：

式中：δl,0为第l条经验数据被初次添加入经验回放缓冲区时的TD-error；δmax为经验回放缓冲区B内最大TD-error，其作用是使δ很小的经验数据仍至少能被采样一次。

2.2.2 智能体训练流程

基于深度强化学习方法的IES 低碳经济调度模型如图3 所示。

图3 IES 低碳经济调度的深度强化学习模型Fig.3 Deep reinforcement learning model of IES low-carbon economy dispatch

图3 中智能体的训练具体流程如下。

1）初始化3 个现实网络参数，即θ1、θ2、φ；以同样的参数值初始化3 个目标网络参数，即θ1′←θ1，θ2′ ←θ2，φ′←φ。

2）设置经验回放缓冲区B 容量和训练时的采样数据条数N。

3）获取并添加经验数据元组至B 中。

①从历史数据中随机取初始状态st。πφ结合噪声x在状态st下选取动作at：

②以动作at与环境交互，从而获得奖励值rt与下一状态st+1，并组成一条数据元组(st,at,rt,st+1)。

③以数据的δ作为其优先级指标，并按数据添加顺序依次存入Summation tree 叶节点中，同时更新相关节点的节点值。

④判断B 中经验数据条数。若数目未达到设定容量上限，则令此时的st+1作为步骤②中的st，并重复以上步骤；否则结束添加并将B 内最大δ赋予每条数据。

4）基于Summation tree 采样方式，从B 中采样出N条数据，并对每条数据以φπ′添加1 个基于目标策略平滑正则化的噪声x′，得出st+1对应的目标动作at+1：

5）记录所得(st+1,at+1)和观测到的奖励rt+1，输入2 个Critic 目标网络从而计算目标值yt。

6）基于梯度下降算法，最小化目标值与观测值间的误差，从而更新2 个Critic 现实网络参数θ。

7）以学习率τ1对现实网络和目标网络参数进行加权平均，软更新目标网络参数。

8）重新计算数据δ并更新其所在叶节点和相关节点节点值。

9）待Critic 网络更新过d步后，同样以梯度下降算法更新Actor 现实网络的参数φ。

10）以学习率τ2来软更新Actor 目标网络参数。

循环步骤4）～10），并记录奖励值。

3 算例分析

3.1 算例设置

采用如图1 所示的IES 作为算例。其中，各设备参数与相关成本系数如表1 所示，IES 与主电网交互时的峰、平、谷时段划分如表2 所示，分时电价信息如表3 所示。根据我国南方某地历史数据，分布式电源出力、电负荷、热负荷需求预测结果如图4 所示。

表1 各设备参数与相关成本系数Tab.1 Equipment configuration information and related cost coefficient

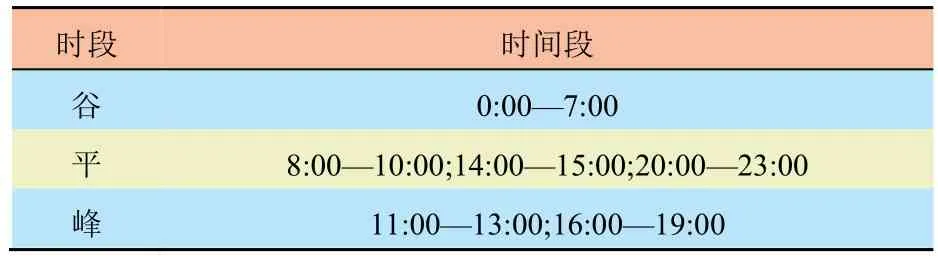
表2 主电网分时电价策略时段划分Tab.2 Time division of TOU electricity price strategy for main grid

表3 主电网分时电价信息表Tab.3 TOU electricity price of the main grid 元/kW·h

图4 负荷、风光出力预测曲线Fig.4 Prediction curves of load,wind power and photovoltaic output

所有算例测试在相同硬件及Python 语言环境中运行。采用基于数据流编程的符号数学系统TensorFlow2.5 编写DRL 方法的神经网络框架。

以下面4 种方法对计算结果进行对比分析。

方法1。采用NSGA-II 算法的多目标优化调度策略。

方法2。采用DDPG 算法的调度策略。

方法3。采用TD3 算法的调度策略。

方法4。采用改进TD3 算法的调度策略。

方法1 中的NSGA-II 算法，以系统运行成本最低、环境治理成本最低作为优化目标，其决策变量为系统内各个可控出力设备以及主电网购售电能量。参数设置为：种群个数为200；最大迭代次数200；交叉率0.5；变异率0.1。该算法每次只能求单个时刻的解。在进行对比分析时，取整个调度时段中每个时刻整合后的结果。

由于IES 运行涉及时间序列的复杂数据集，所以对于方法2、方法3、方法4 的神经网络，需预设各神经网络的学习率、经验池容量、隐含层层数与神经元个数。DRL 方法采用统一神经网络参数：Actor 网络学习率取0.000 3，Critic 网络学习率取0.003，软更新学习率τ1、τ2取0.005，神经网络隐含层为3 层，采用的激活函数分别为ReLU、ReLU、Tanh，每层64 个神经元，折扣因子取0.95，经验池容量B 取3 000。对于方法3、方法4 中改进前后的TD3 算法，还需设置其他参数：噪声x标准差σ取0.01，x′标准差σ′取0.02，截取边界ψ取0.05。

3.2 结果对比分析

DRL 方法奖励值收敛结果如图5 所示。

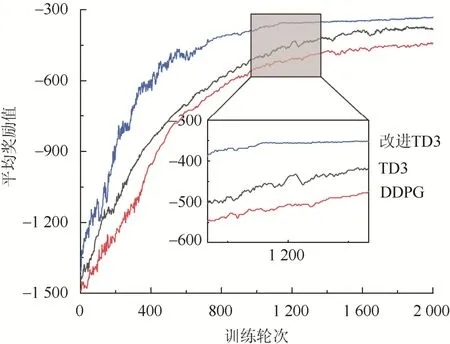
图5 DRL 方法奖励值收敛结果Fig.5 Convergence results of DRL method reward value

由图5 可知，本文所提改进TD3 算法在训练前期出现了平均奖励值明显波动，原因在于：在采样前期，为避免某些数据无法采样，数据优先级指标被赋予统一初值，导致其中某些实际更新价值较低的数据被高估，从而影响了智能体对动作优化的判断；随训练轮次的增加，平均奖励值水平逐渐平缓，在训练达到1 200 轮次后趋于收敛。在同样训练2 000 轮次的条件下，本文算法最高平均奖励值水平略高于未改进TD3 算法，且明显高于DDPG 算法；这说明本文模型能够寻得的最优解，较另外2 种方法更佳。

4 种方法的调度结果如图6 所示。

图6 各方法调度策略功率平衡图Fig.6 Power balance diagram of scheduling strategies of each method

4 种方法的系统运行成本如表4 所示。

表4 各方法系统运行成本Tab.4 System running cost table of each method 元

由图6 可见，4 种方法输出结果都未出现明显的功率不平衡问题。

结合表4 数据可知，在不同方法的输出结果中，各项成本有一定差异：改进TD3 算法对比NSGA-II算法总成本降低了5.48%，比未改进TD3、DDPG算法分别降低了2.29%和7.28%。由表4 中计算结果可知，本文所提方法得到的总污染治理成本以及天然气购气成本低于其他方法，也即天然气消耗量、碳排放量更低；这说明其在提高系统运行经济性、低碳性的效果上表现最好。

TD3 算法改进前后寻优速度验证：设置训练轮次为1 200 轮次。将相同的负荷、分布式电源出力预测数据代入2 种方法，对智能体重新训练。以未改进TD3 算法结果数值为基准，对改进后TD3 算法结果进行折算对比，结果如图7 所示。

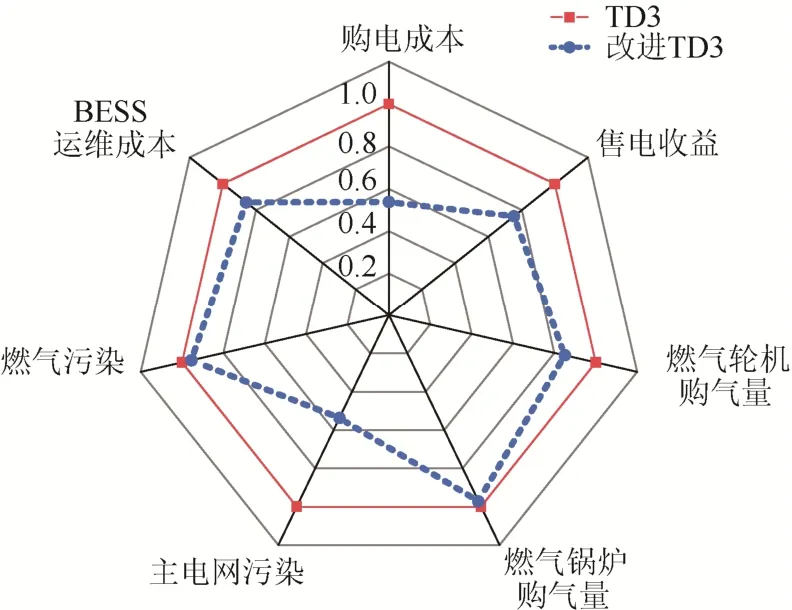
图7 改进前后TD3 算法输出结果对比Fig.7 Comparison of TD3 algorithm output results before and after improvement

由图7 可知，改进后TD3 算法输出结果在系统运行中的各项成本较改进前均有减少。由此可以认为，在同样训练1 200 轮次的条件下，改进后的TD3 算法寻得了更优的策略。

小结：本文所提改进TD3 算法在保留TD3算法优势的基础上，进一步提升了其训练效率，且在所应用的IES 低碳经济调度场景中，较其他3 种方法能更好地兼顾系统运行的低碳性与经济性。

4 结论

本文针对IES 的低碳经济调度，提出了一种以Summation tree 改进TD3 算法中经验数据采样的DRL 方法。与现有方法相比，本文所提方法有以下优势：

1）该方法能够从数据中自适应学习并挖掘物理模型。随着训练轮次的增加，该方法能够不断优化策略使其趋于最优，从而克服了在处理某些高维复杂问题时需要手动编写规则和模型的困难。

2）与计算效率较高、收敛速度较快的确定性策略梯度算法相比，本文方法智能体的动作探索能力更强，陷入局部最优的可能性更低。

3）对比改进前，所提出的改进方法实现了对更新价值较大的经验数据的高效利用，有效避免了相似经验数据降低训练速度的问题。

展望：本文所提改进TD3 算法，通过对历史经验数据采用Summation tree 进行存储采样，实现了确定性策略方法的优先经验回放机制；作为一种加权采样方法，其在IES 低碳经济调度问题的复杂能源调度环境、多市场需求应用场景中具有良好的适用性、可优化性与自适应性。然而，本文研究中未充分考虑系统运行中实际存在的损耗以及调整奖励值函数中各成分权重。未来的研究，将针对扩展系统复杂性、引入多智能体结构、调整不同奖励值权重对比输出策略差异等方面展开。