基于加权投票的主动密度峰值数据聚类算法

张苏颖 许曙青

1(江苏联合职业技术学院南京工程分院 江苏 南京 210035)

2(南京理工大学计算机学院 江苏 南京 210000)

0 引 言

由于聚类在无监督学习中起着重要的作用,许多聚类方法得到了广泛的研究,包括谱聚类、层次聚类等[1-2]。密度聚类方法与半监督策略结合起来的方法可以解决标签样本数量不足的问题,这种方法基于随机选择的类边界信息,由于随机选择成对约束会导致冗余和噪声,继而文献[3]提出了一种主动聚类策略。

主动聚类采用的成对约束选择策略已经存在许多方法。文献[4]通过查询具有代表性的实例实现初始化来构造邻域,邻域由一组已知属于同一个聚类的实例组成。文献[5]利用邻域的概念为每个聚类至少发现一个实例。然而,仅仅通过简单地使用具有代表性的实例是不够的。选择信息实例可以减少局部和全局的不确定性。

主动聚类查询过程分为静态选择和动态选择两个阶段,其中前者在半监督聚类前产生完全约束集,忽略聚类结果。文献[6]在训练阶段选择了约束条件,以构建邻域关系。文献[7]通过流形学习获得边界信息,以促进半监督聚类。后者在每次迭代中重复查询和标签更新的过程。文献[8]重复进行半监督聚类,以选择信息门户文档。文献[9]迭代地利用模糊超球体通过主动学习来发现和改进集群。文献[10]通过最小化约束谱聚类后的期望误差迭代地获得约束。上述主动聚类方法均利用代表性或信息性实现查询选择,然而,没有同时考虑代表性和信息性,使得查询选择提升效果有限。另外,上述方法还必须无效地重复半监督聚类更新标签,降低了计算效率。

针对上述问题,本文提出一种基于加权投票一致性的主动密度峰值数据聚类集成算法(Active Density Peak Ensemble Algorithm, ADPE),通过数据集验证可以发现提出的方法有效解决了上述问题,并展示了良好的聚类性能。

1 基本理论

1.1 主动聚类集成框架

局部不稳定性的一个缺点是它无法测量聚类模型实例的划分难度。例如,在图1中,每个矩形虚线框表示两类数据集的边界区域的可能的聚类结果,总共有s个聚类结果。特别地,来自上下区域的实例形成了两个边界区域。这些实例分为两个集群。显然,实例2由于其不稳定的分区标签比实例1更模糊。然而,实例1和实例2具有相同的局部不稳定性。在这种情况下,有必要考虑全局不稳定性来估计每个实例的划分难度。

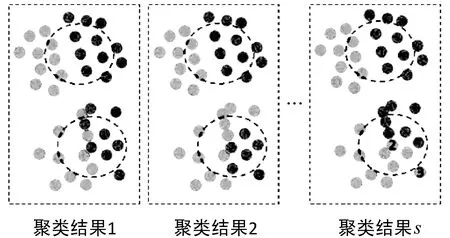
图1 两类不确定性问题的可能聚类结果

如图2所示,为了进一步提高性能,提出主动聚类集成方案。首先,ADPE生成特征子空间以提供多角度视图和各种信息。主动密度峰值(Active Density Peak, ADP)模型独立应用于每个子空间,并且这些模型共享一个公共邻域集。在静态选择阶段,为了构造初始邻域,通过考虑所有子空间中的γ来选择代表性实例。在动态选择阶段,通过结合局部和全局不稳定性来迭代选择信息实例。最后设计一个实例级加权投票聚类方法,对多个成员进行集成,从而得到最终的聚类结果。

图2 ADPE方法计算框架

1.2 初始化

采用高斯核来量化局部密度,其表示为：

(1)

式中：dij是xi和xj之间的距离。由于不同数据集的截止距离dc难以估计,根据文献[11]估计了dc,使得邻域的平均数目约为实例总数的(100α)%,其中α∈[0,1]是一个参数。dc计算式如下：

(2)

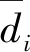
(3)

由于每个实例都与另一个具有更高密度的实例相连接,因此构造了一个具有多分支的树状图,称为归属树,其中每个节点代表一个实例。如果满足δi=d(xi,xj),则密度最高的实例是根节点,节点j是节点i的父节点。根据文献[11],归属树表示实例之间的关系,其中父节点的标签被分配给其子节点。

L(xi)=L(parent(xi))

(4)

式中：L(xi)是xi的标签,parent(xi)是归属树中xi的父节点。密度峰值聚类假设聚类中心被局部密度较低的实例包围,而远离任何局部密度较高的实例。这个性质分别用ρ和δ来测量。因此,通过ρ和δ计算γ来表示实例成为聚类中心的概率,其计算式为：

(5)

1.3 静态代表性实例选择

从特征子空间的角度看,实例具有不同的聚类中心概率。为了综合考虑所有子空间,ADPE计算γ的平均值来评估其代表性的强弱,其计算式如下：

(6)

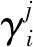
1.4 动态信息实例选择

ADPE中每个实例的局部不稳定性的计算如下：

(7)

(8)

(9)

(10)

(11)

其中：

(12)

(13)

它利用熵来评估在所有聚类结果中被划分为同一集群的实例的稳定性。由于图1中的实例2和实例3始终被划分为同一集群,所以它们具有相同的全局不稳定性。但是,实例2更靠近边界中心,而且它应具有更高的查询优先级。为了克服这两种不稳定性的缺点,将局部和全局不稳定性组合起来,计算式如下：

UADPE(xi)=Ul(xi)+Ug(xi)

(14)

较大的UADPE(xi)说明xi中包含较多的信息。不稳定性最大的实例由以下公式得到：

(15)

采用快速更新策略对每个子空间的聚类结果进行细化。不稳定性采样和标签更新迭代运行,直到满足条件q≥qmax才停止。

2 方法简介

2.1 计算流程

为了整合所有改进的聚类结果,本文设计一种实例级加权投票一致性聚类方法。尽管传统的投票方法简单和快速,但是它有两个局限性：(1) 应该将标签事先进行对齐;(2) 在每个聚类结果中都没有考虑实例的置信度。值得注意的是,每个子空间中的标签已对齐,因为公共邻域集为每个聚类提供了统一的标签。实例的置信度用局部不稳定性来评估,每个实例的加权投票标签定义如下：

(16)

其中：

(17)

式中：1-Uj_ADP(xi)是对Fj的置信度权重。最后的聚类结果用L={V(x1),V(x2),…,V(xn)}表示。具体算法如算法1所示。

算法1ADPE

输入：X,qmax,s,ξmin,ξmax,αmin,αmax。

输出： 聚类结果L。

1. for j = 1 to s do

2. 用随机特征抽样率生成特征子空间Fj

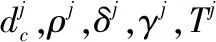
4. end for

5.通过式(13)计算统一质量γ;

6.确定滑动窗口半径r,以随机选取的中心点C半径为r的圆形滑动窗口开始滑动,不同的数据集半径的确定通过自适应半径方法计算得到,具体方法参考文献[9]。通过滑动窗口得到潜在集群中心P={xω1,xω2,…,xωt-1};

7. for each inPdo

8. for eachNk∈Ndo

9.通过任何实例xk∈Nk;q=q+1查询xp;

10. if (xp,xk)∈MLthen

11.Nk=Nk∪{xp};L(xp)=k;break;

12. end if

13. end for

14. if 未得到MLthen

15.η=η+1;Nη={xp};N=N∪(〗Nη};L(xp)=η;

16. end if

17. end for

18. 通过式(4)从每个子空间得到s的初始聚类结果;

19. repeat

20. 由式(14)-式(15)得到确定性最差的实例x*;

21.通过每个满足查询x*;

22. for each subspaceFjdo

23. 采用快速更新策略更新标签;

24. end for

25. untilq≥qmax

26. 通过式(16)和式(17)计算实例级加权投票标签作为最终结果;

27. 得到最终的聚类结果L={V(x1),V(x2),…,V(xn)};

2.2 复杂性分析

本文分析了ADP和ADPE的时间复杂性。首先,ADP的时间复杂性可以由式(18)得到。

TADP=TINIT+TSRIS+TDIIS

(18)

式中：TINIT、TSRIS和TDIIS分别是初始化、静态代表性实例选择和动态信息实例选择的时间复杂性。TINIT依赖于计算成对距离的预处理阶段,即O(n2m)。当集群中心数C远小于n时,TSRIS=O(C·n)=O(n)。在动态选择的每次迭代中,计算局部不稳定性和快速更新策略的时间复杂度分别为O(K·n)和O(n),其中K是平均邻域数。因此,当TDIIS=O(qmax·(K·n+n))=O(n)时,qmax和K是取值较小的常数。总体而言,TADP计算如下：

TADP=TINIT+TSRIS+TDIIS+TCM=

O(s·n2·ξ·m)+O(n)+O(s·n)+

O(s·n)=O(sn2m)

(19)

随着子空间s的数量增加,计算成本也随之线性增加。与基于协关联矩阵或图的聚类方法复杂度分别为O(n2)和O(n3)的时间复杂度不同,本文提出的聚类方法将成本降低到O(n)。由于主要的计算费用都花在了初始化上,所以可以使用分布式技术或一些预分组方法来加速初始化计算。时间复杂度对比如表1所示。

表1 不同的发射式聚类和加速方法的时间复杂度比较

大多数最新的主动聚类方法通过重复耗时半监督聚类来更新标签。在表1中列出了不同半监督聚类的时间复杂度和一些提高运算速度的方法。当m和n都很大时,半监督k-means的时间复杂度高于快速更新策略,并且难以识别任意形状的集群。半监督谱聚类中的标准特征向量的时间复杂度为O(n3),这并不能运用到大规模数据集上。虽然可以应用一些提高运算速度的方法,但是由于抽样和投影采用随机方法,近似方法可能无法充分利用边界信息。此外,URASC在不稳定性估计运算中要求精确的特征值,近似方法并不适用。

3 实验与结果分析

3.1 数据集和实验方法

本节用归一化互信息(Normalized Mutual Information,NMI)和调整兰德指数(Adjusted Rand Index,ARI)对18个数据集(包括8个UCI数据集)和10个具有高维特征的基因数据集(D-9-D-18)进行了性能评估[12]。表2记录了关于这些数据集的信息,其中c、n和m分别是集群、实例和特性的数量。

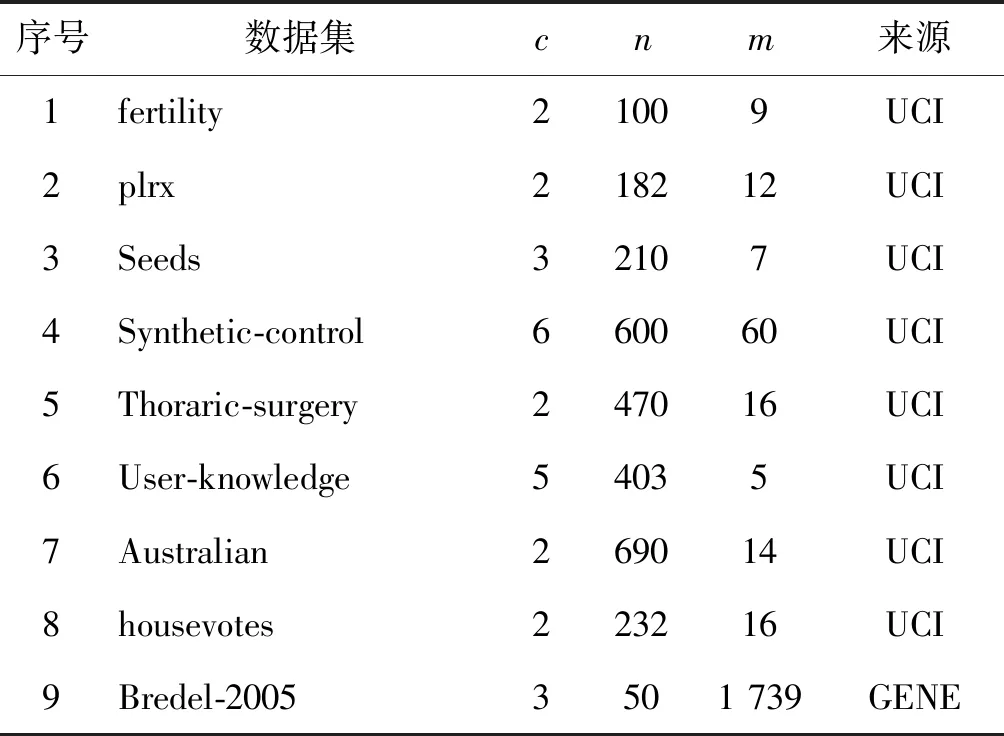
表2 相关数据集信息

为了验证本文方法的性能,比较了其他算法。首先,ADP和ADPE的参数值设置如下。

(1) ADP：l=5,θ=0.000 01 andα=0.22。

(2) ADPE：s=10,[ξmin,ξmax]=[0.6,0.8] and [αmin,αmax]=[0.15,0.30]。

由于ADP是一种单一的主动聚类算法,将其与随机选择成对约束的两种半监督聚类方法和三种使用邻域的主动聚类方法进行了比较。

(1) COPKM[4]：半监督k均值聚类方法,在聚类时可以避免违反约束条件。

(2) E2CP[5]：基于k最近邻图的成对约束传播方法。令μ=0.5和k=10,作为最佳聚类结果的参数值。

(3) APCKM[7]：主动k均值聚类方法,可以查询具有代表性的实例以获得更好的初始化效果。令w=1.0,与文献[7]参数值相同。

(4) URASC[8]：主动光谱聚类方法,可以查询信息量大的实例,最大程度地减少不稳定性。计算了b=(1/2)n个实例的梯度,并令最大尺寸k=10。

(5) NPU[9]：适用于任何半监督聚类算法的主动聚类框架。在URASC中使用相同的半监督谱聚类方法,并将随机森林的大小设置为50。

此外,将ADPE与聚类集成方法进行了比较,包括两种半监督集成方法和两种主动聚类集成方法。这些方法中的集合成员数与ADPE相同,均为10个。

(1) GCC[10]：基于图像的聚类集成框架。将E2CP作为基本聚类模型。

(2) RSEMICE[11]：优化聚类结果置信因子的自适应半监督聚类集成方法。将参数大小和原文设置一样,μ=0.5,α=0.33,ζ=0.25。

(3) FACE[12]：基于全局不稳定性选择成对约束的主动聚类集成方法。

(4) ACCE[13]：基于boosting的聚类集成方法,主动选择需要查询的实例对。

3.2 参数值的影响

(20)

若得到的偏差较小,表示它更接近最小查询时间。将[0.0,0.5]分为10个区间,计算18个数据集的平均标度偏差,结果如表3所示。可以发现,当α在0.20到0.25之间变化时,ADP查询效率最高。在ADP中令α=0.22,在ADPE中令[αmin,αmax]=[0.15,0.30]。

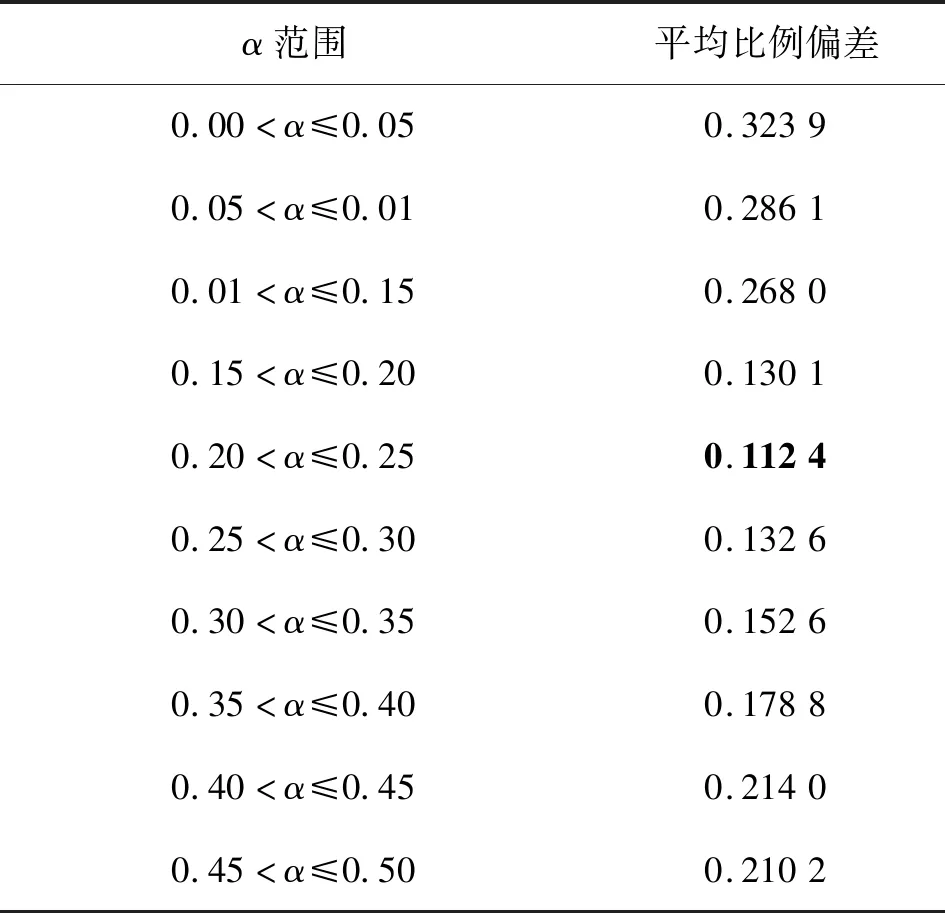
表3 α对18个数据集影响的分析总结

3.3 ADP与单聚类算法的比较

比较了ADP与COPKM、E2CP、APCKM、NPU和URASC在18个具有不同查询次数的数据集的NMI值。结果如图3所示。在设置相同的查询数量时,ADP在大多数数据集上的NMI值总体上高于其他方法。ADP的性能随着查询量的增加而稳定增加。然而,NPU和URASC在一些数据集上运行的结果有些波动,如Seeds、Synthetic-control和housevotes。可能是因为一些约束条件混淆了半监督聚类算法。此外,在18个数据集上采用ADP、NPU、URASC和APCKM方法,直到所有实例都能正确地实现聚类(NMI和ARI为1.0)。该方法使用的查询数量越少,就越有效地利用了边缘信息。结果如表4所示,其中“+”表示该方法无法收敛到NMI和ARI为1.0,即使它的查询数量是ADP的两倍。ADP对18个数据集中的15个数据集使用最少的查询,说明它可以充分利用边界信息。在表5中,记录了多项统计检验(Friedman’s test, Bonferroni-Dunn’s test, Holm’s test, Hochberg’s test, and Hommel’s test)。得出的主要结论是零假设(qADP的显著性比qNPU、qURASC和qAPCKM更小)在0.05的显著性水平被拒绝。因此,算法ADP在查询利用率方面优于其他方法。

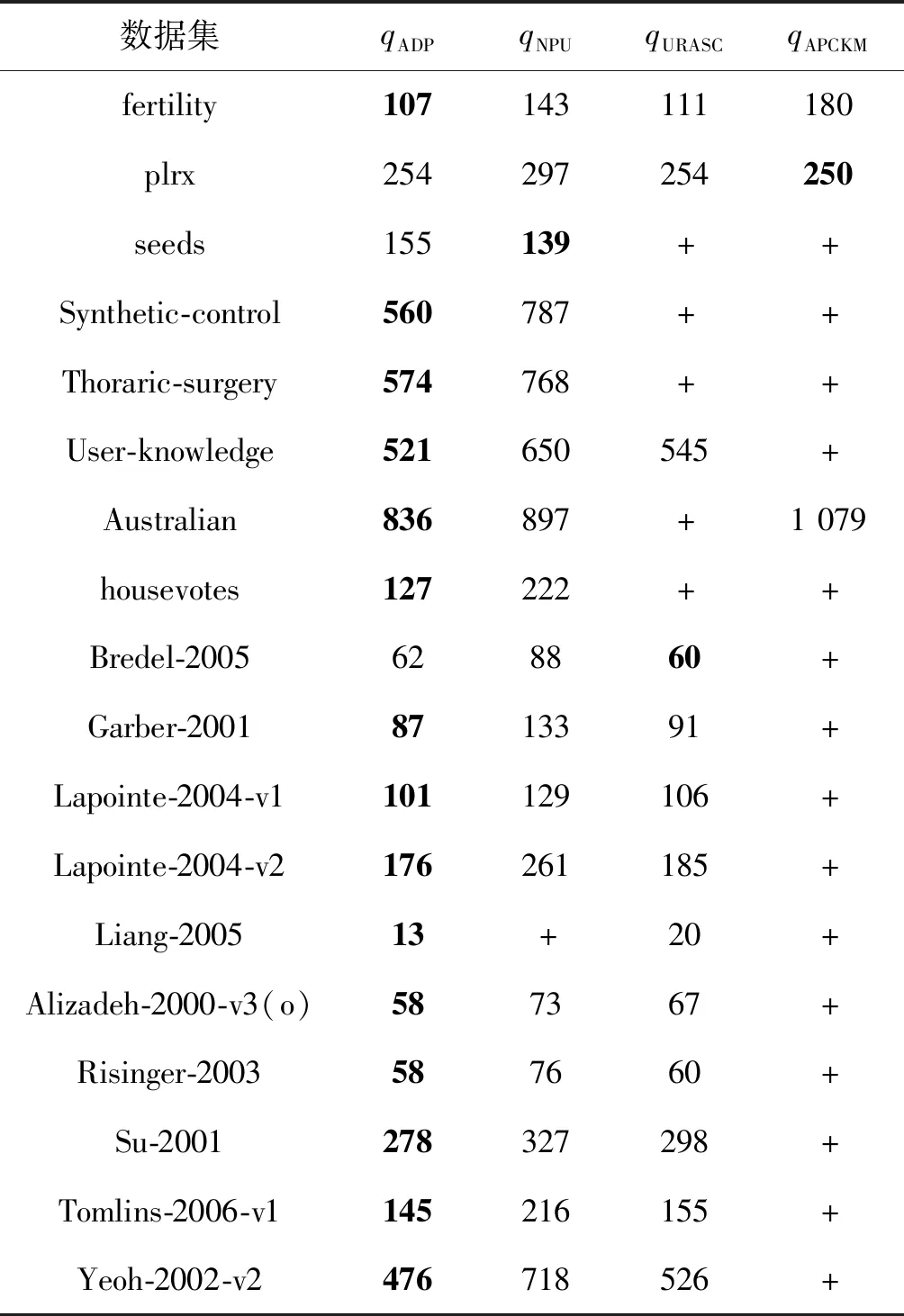
表4 不同的主动聚类算法的查询数量

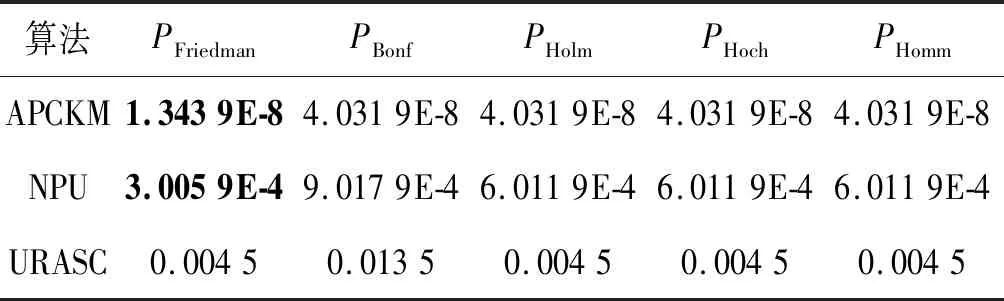
表5 不同算法多项统计检验值对比

3.4 ADPE与聚类集成的比较

ADPE采用随机子空间来提供不同的信息,可以有效地减少噪声和冗余特征对高维数据的影响。然而,这对于低维数据集没有多大意义,因为可能会删除一些关键特征。因此,在10个基因数据集上比较了ADP、GCC、RSEMICE、FACE和ACCE的性能。表6记录了有关ARI的比较结果,其中粗体表示最佳结果。与ADP相比,ADPE在整体性能方面表现更好,主要有两个原因：(1) 结合局部和全局不稳定性,有效地选择信息实例;(2) 将不同的集成成员聚类以获得更全面的结果。此外,ADPE性能明显优于FACE、ACCE、RSEMICE和GCC。其原因可能是：(1) 在处理高维数据时,FACE和ACCE中的基本聚类模型不能提供良好的聚类结果;(2) RSEMICE和GCC由于约束条件的随机选择,不能充分利用边缘信息。

3.5 局部/全局不稳定性的影响

由于局部不稳定性和全局不稳定性各有优势,因此结合它们来选择信息最丰富的实例以获得更好的性能。首先仅使用局部不稳定性(ADPE-L)或整体不稳定性(ADPE-G)来测试ADPE的性能,如图4和图5所示,将局部和全局不稳定性相结合可以在百分之八十的数据集上获得最佳性能。局部不稳定性在实例中确定边界区域,在模型级别添加全局不稳定性可以找出混淆性最大的实例。因此,局部和全局不稳定性的组合具有非常满意的性能。

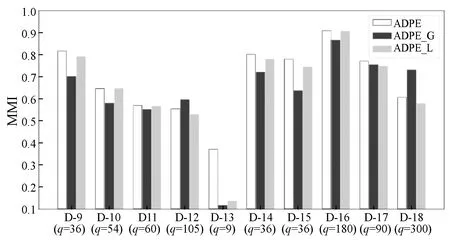
图4 局部和全局不确定性对NMI性能的影响

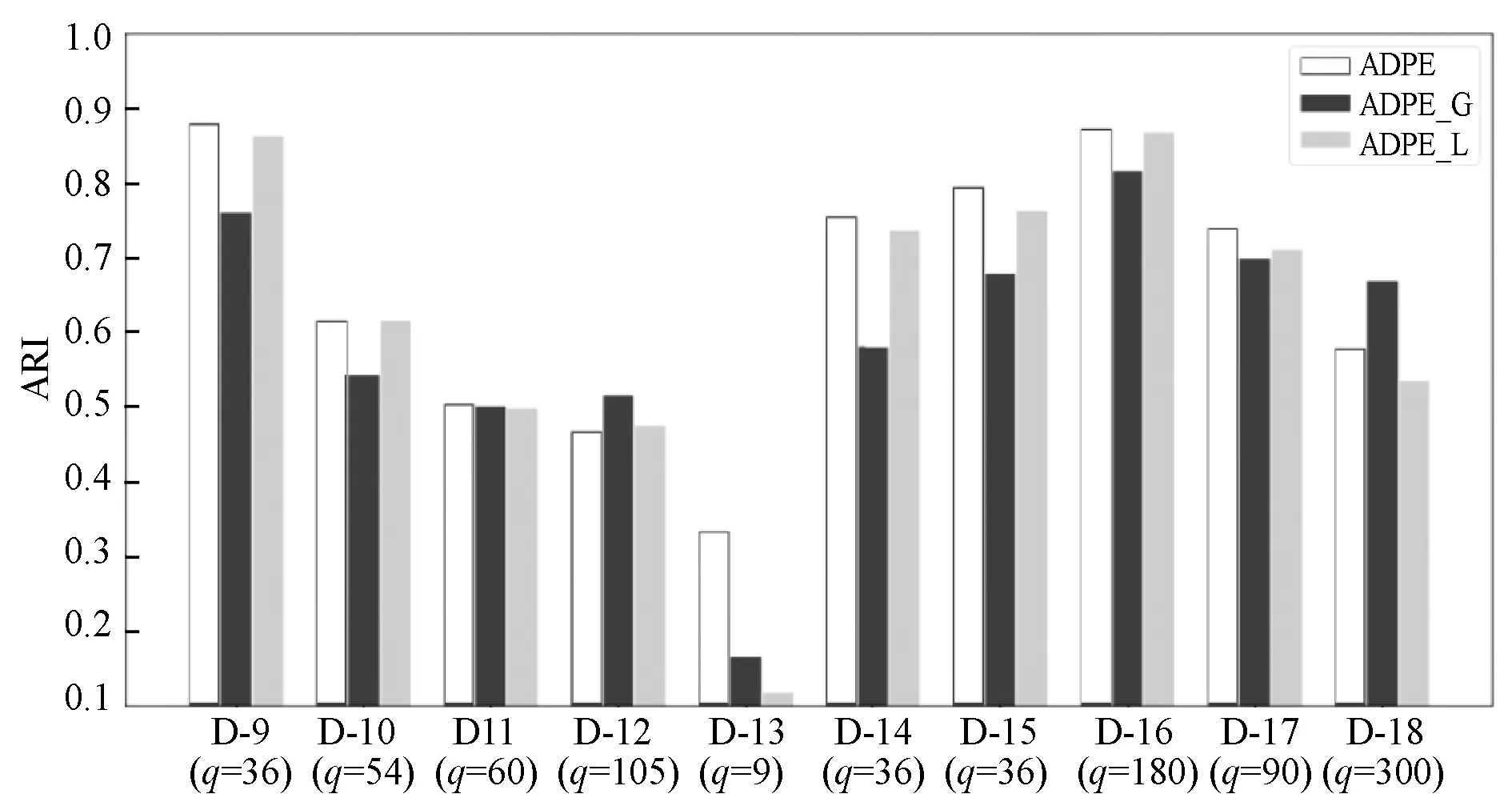
图5 局部和全局不确定性对ARI性能的影响

3.6 发现未知集群的能力

基于邻域的主动聚类方法可以在不需要已知聚类数目的情况下找到未知聚类。ADP和ADPE为每个邻域查询代表性实例,为了方便给数据集分配标签。但是,URASC、NPU和APCKM是通过使用其所有相关实例来构建邻域。表7记录了这些方法用于发现所有集群所需的平均查询数量。虽然本文方法在查询未知集群方面并不比其他方法明显优越,但其代表性的实例对标签分配任务的贡献较大。

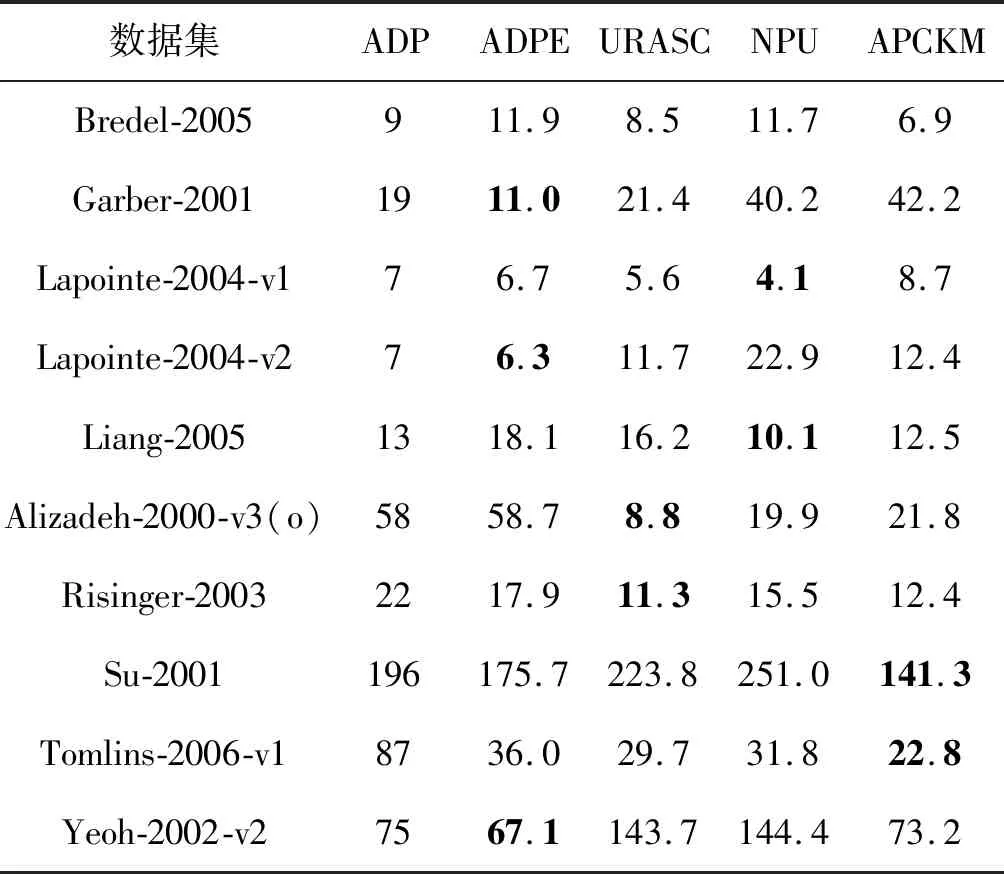
表7 通过不同的基于邻域的主动聚类方法查找所有聚类的平均查询数量

3.7 聚类方法的比较

ADPE通过提出的实例级加权投票聚类方法整合了多个聚类结果。将其与三种备选聚类方法进行比较：基于投票方法(APDE_V)[14]、基于关联矩阵方法(ADPE_CAM)[15]和基于图像方法(ADPE_NCUT)[16]。 图6和图7描绘了这些方法在NMI和ARI方面的性能。可以看出,在大多数数据集上,本文方法优于其他方法。原因可能是本文方法考虑了每个子空间中实例的置信度,并降低了低质量标签产生的影响。另外,避免了排列过程,从而使本文方法更加有效。

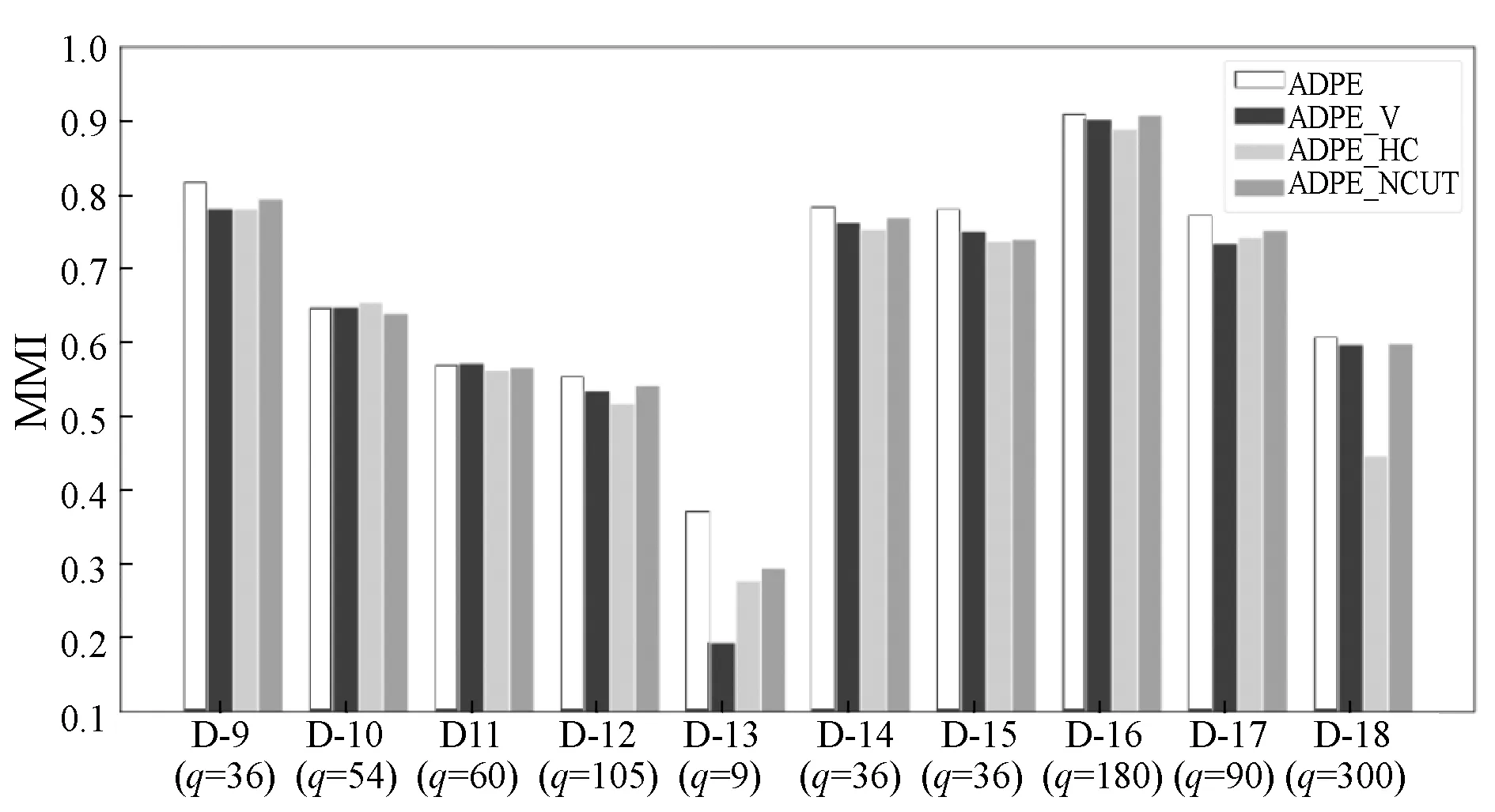
图6 基于NMI的一致性方法比较

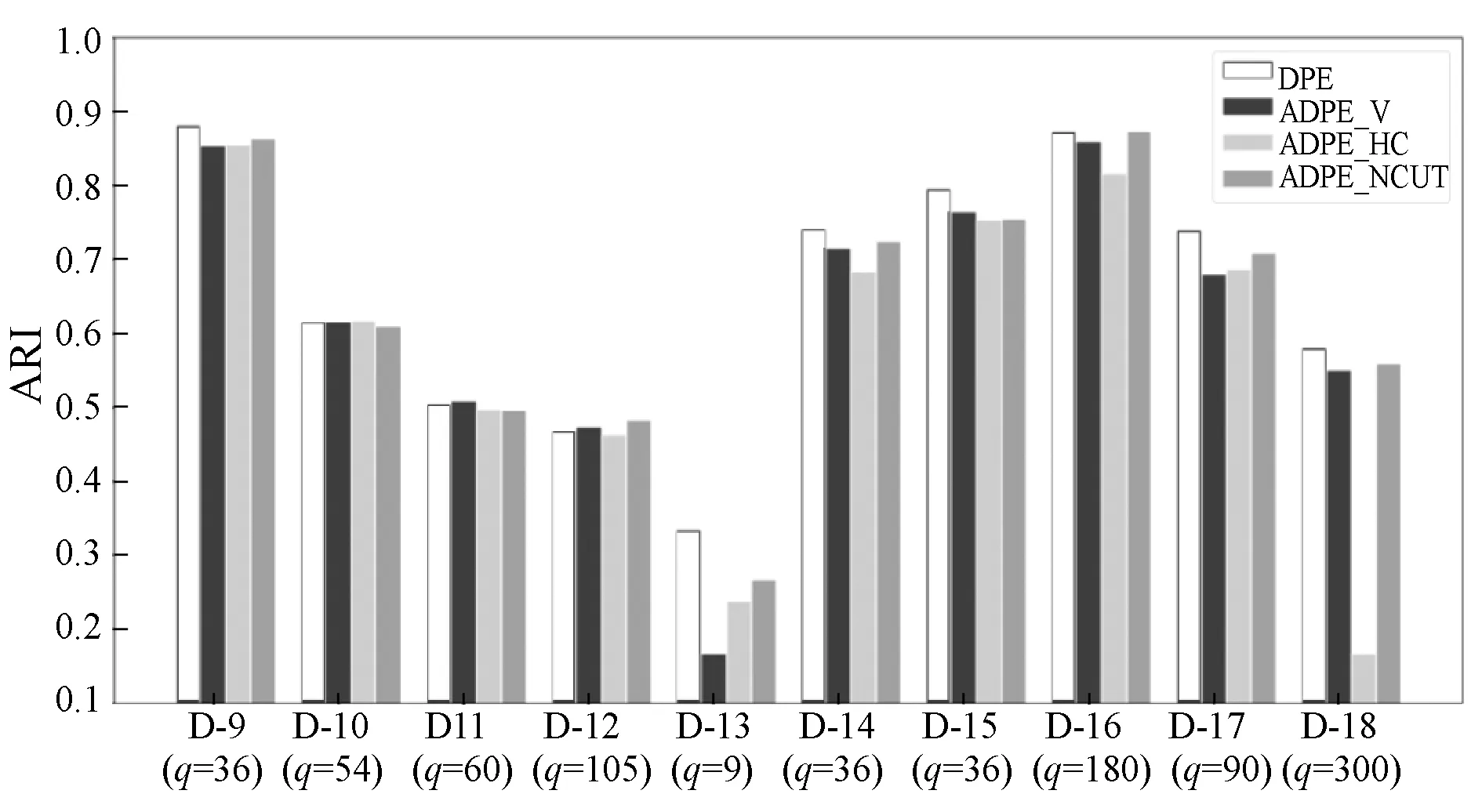
图7 基于ARI的一致性方法比较

3.8 本文算法在大型数据集上的表现

表8记录了不同方法在6个较大的数据集上的运行结果。前4个UCI数据集涵盖了不同的领域,包括图像、生物信息学、文本和医学。其中,MSD是百万首歌曲数据集的子集,由4种音乐风格(流行、电子、说唱和爵士乐)的8 000个实例组成,其中每个类有2 000个实例,一共提取了124种特征。RLCTS包含53 500个实例,从CT图像中提取了384种特征。采用适合大数据的聚类算法(Mini Batch K-Means)对RLCTS中的相邻实例进行预分组,并为所有方法生成5 000个具有代表性的实例。图8显示了本文方法(ADP和ADPE)和4种主动聚类方法(NPU、URASC、APCKM和ACCE)以及两种半监督聚类方法(E2CP和GCC)在NMI方面的性能。考虑到效率问题,当n≥5 000时不适用URASC。与APCKM、ACCE、E2CP和GCC不同,本文方法不需要预先知道集群的真实数量,因此,在某些数据集(如cnae_9、MSD和RLCTS)上的性能可能会受到影响。然而,随着查询量的增加,ADP和APDE的性能都显著提高,并且最终在大多数数据集上的性能优于其他方法。结果表明,ADP和APDE在大型数据集上是可扩展的,预分组方法可以减少算法运行的时间,提高效率。

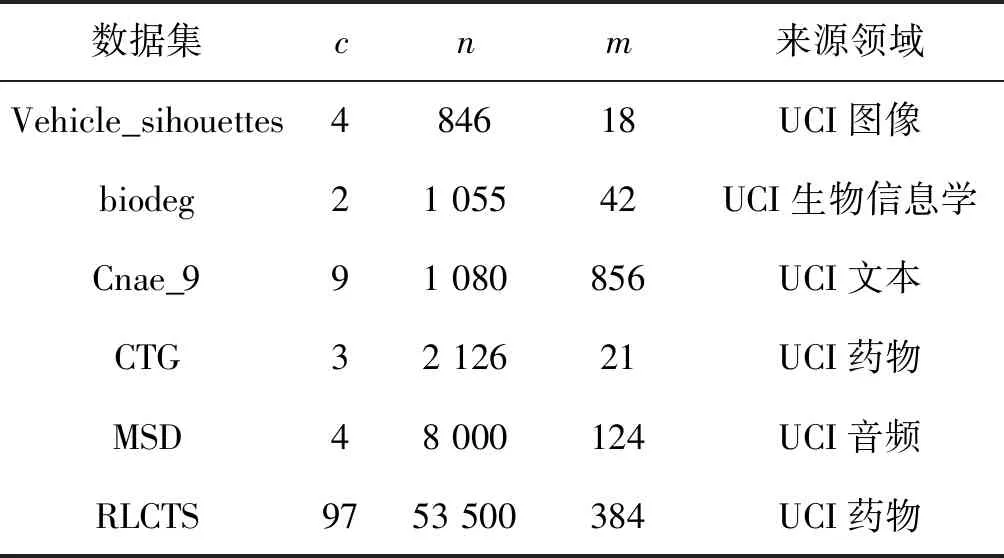
表8 有关6个大数据集的统计信息

图8 基于NMII的6大数据集不同方法的性能比较

3.9 运行时间的比较

为了有效地更新标签,本文设计了快速更新策略。2.2节比较了不同的标签在更新算法时的渐近计算复杂度。本节评估了这些方法在4个数据集上的运行时间。所有这些方法均基于Scikitlearn[17],计算机的CPU为Intel 6核i7-8700K,主频为 3.70 GHz。表9记录了不同方法更新一次标签所需的平均运行时间。PI表示加速方法采用的是幂迭代[18]。本文还基于PyTorch[19]框架,在1080Ti的GPU平台上重复以上方法(例如MPCKM-GPU、semiSC-GPU和E2CP-GPU)。与CPU相比,GPU可以减少运行时间。该方法在CPU和GPU的运行时间有很大的区别,GPU明显优于CPU。随着数据量的增加,优势变得更明显。原因可能是快速更新策略不涉及复杂的操作,只遍历归属树中选定的节点子集来更新标签。

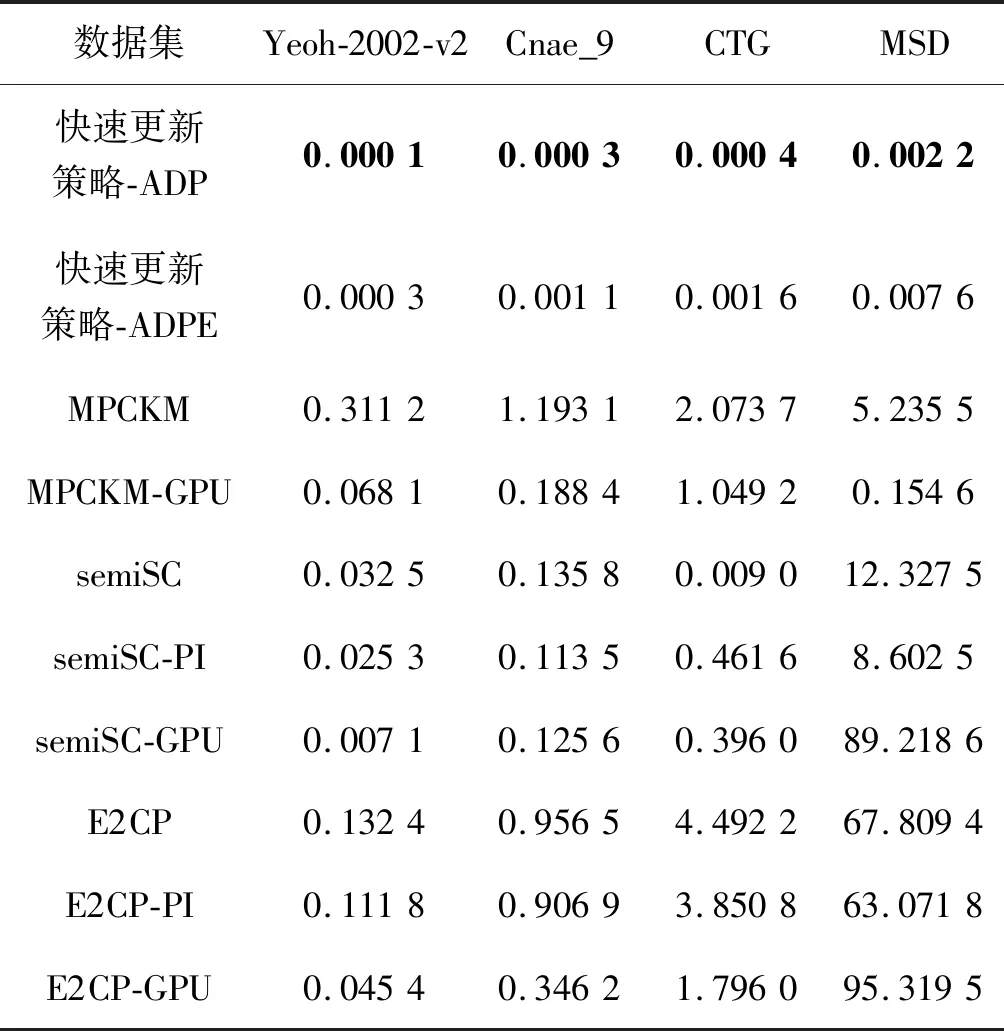
表9 不同方法更新一次标签所需的运行时间 单位：s

4 结 语

针对传统方法缺乏对查询标准的全面考虑,并且反复运行半监督聚类来更新标签等问题,提出一种基于加权投票一致性的主动密度峰值集成数据聚类算法。通过数据集验证结果分析可得出如下结论：

(1) ADPE能充分利用边缘信息,结合了局部不稳定性和全局不稳定性,在整体性能方面表现更好。

(2) 局部不确定性和全局不确定性的结合有助于选择最模糊的边界实例,以更好地分离聚类。

(3) ADPE采用随机子空间来提供不同的信息,可以有效地减少噪声和冗余特征对高维数据的影响,并且查询利用率方面优于其他方法。

(4) ADP和ADPE由于采用了快速更新策略,在效率上有很大的优势,并且ADP和APDE在大型数据集上是可扩展的,预分组方法可以减少算法运行的时间,提高效率。