基于点线配准和超像素分割的图像拼接算法

蒋 敏 蒋品群* 宋树祥 夏海英 李加亮

1(广西师范大学电子工程学院 广西 桂林 541004)

2(浙江邮电职业技术学院人工智能学院 浙江 绍兴 312366)

0 引 言

图像拼接算法是对两幅或多幅具有一定重叠部分的图像进行拼接,最终拼接成一幅包含输入图片信息的新图像[1]。

特征点配准是图像拼接的关键,Lowe[2]首次结合高斯模型和尺度空间,提出了基于尺度不变的特征变换(SIFT)算法。该算法稳定性强,但速度慢。Rublee等[3]采用二进制描述子,提出ORB算法,配准速度得到提升,但稳定性变差。边佳旺等[4]在ORB算法的基础上,提出基于网格运动统计(GMS)算法,速度快、稳定性高,但存在误匹配。Li等[5]将单应性应用到图像中的直线匹配,提出了分层线匹配(HLM)算法,得到了高鲁棒性的线匹配,为图像拼接方法引入线特征奠定了坚实的基础。针对目前图像拼接算法采用单特征点配准,存在特征点丰富度不足,且存在误匹配点的问题,本文在单特征点基础上引入线特征匹配,并利用投影误差约束以保证特征点的精准性。

图像翘曲是图像拼接的重点,Zaragoza等[6]提出尽可能投影变形(APAP)算法,将图像进行网格划分,分块计算局部单应性以完成翘曲,图像得到较好的对齐。Lin等[7]将单应性线性化,提出逼近自然变形(AANAP)算法,解决了透视失真问题。Li等[8]利用插值函数提出了基于鲁棒性的弹性翘曲(REW)算法,对齐精度得到提升。但是,当输入图像具有较大视差时,以上算法均出现图像未对齐、重影等现象。原因在于刚性的网格划分破坏了图像完整性,选取的映射中心点不够准确,而中心点的准确度将直接影响拼接效果。为解决上述问题,本文利用超像素分割[9-10]算法对图像进行保护性分割,得到精准的映射中心点,提高了图像对齐精度,能输出更高质量的拼接图。

1 算法主要思想

本文的图像拼接算法流程如图1所示。首先输入具有重叠部分的两幅图片,使用SIFT、ORB结合GMS算法进行特征点提取与配准,并引入直线特征,结合单应性矩阵将直线特征点映射[11],映射偏差值作为约束以筛选匹配点;然后引入超像素分割代替刚性网格分割以更精准地划分图像,得到子图像块的中心点,在重叠区域进行局部翘曲,非重叠部分进行全局翘曲。最后使用余弦函数对图像进行加权融合,输出高质量的拼接图像。

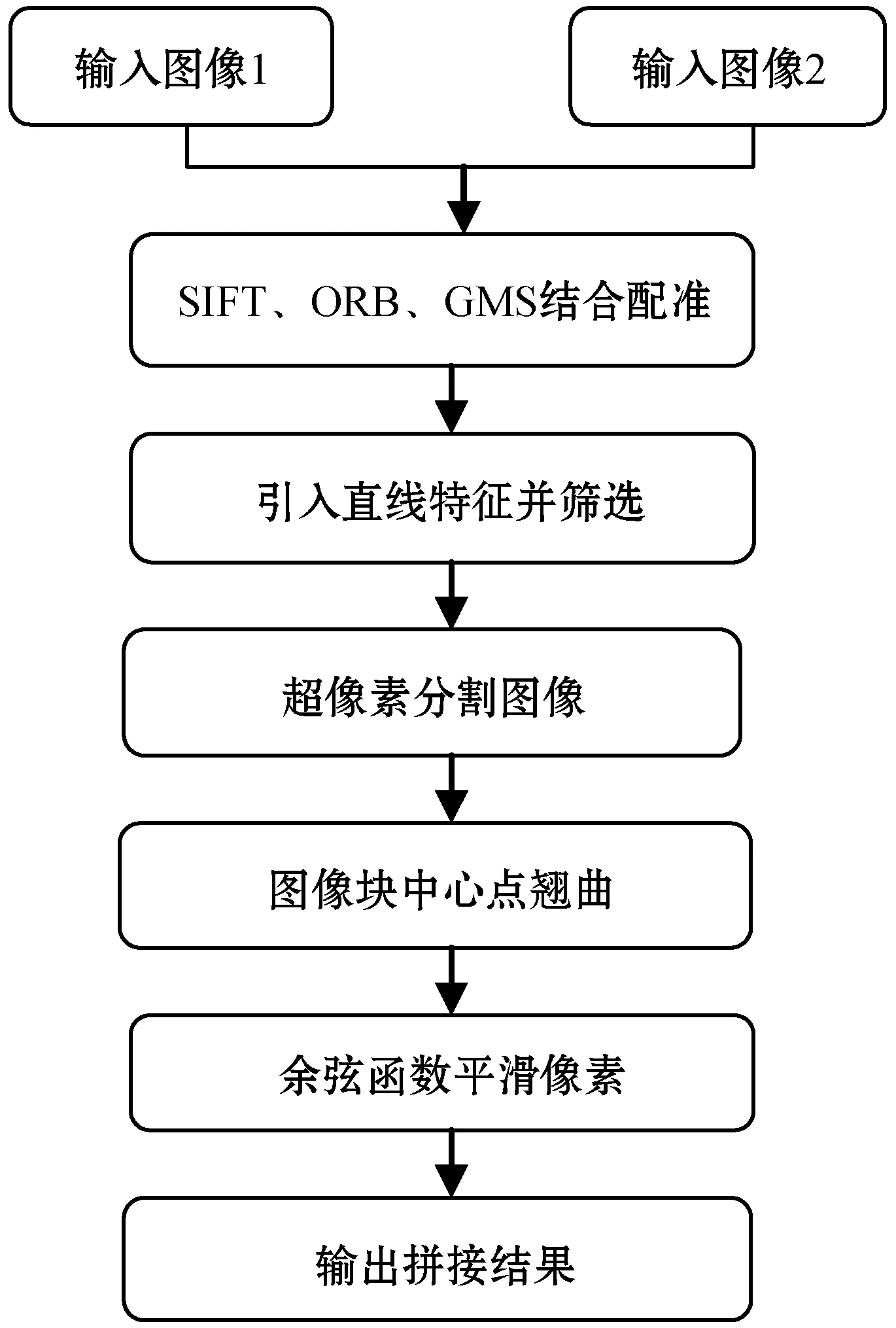
图1 本文拼接算法流程

2 特征点配准

特征点的提取与配准是图像拼接的第一步,本文利用SIFT、ORB结合GMS的策略对图像的特征点进行提取和配准,以实现保留特征鲁棒性的同时提升匹配精度[12-14]。线特征是图像的又一重要特征,但是在图像拼接研究中往往被忽略,并且,随着线匹配的鲁棒性的提升,为图像特征匹配中引入线端点提供了坚实基础。为此,本文使用了基于LSD(Line Segment Detector)描述符的直线特征匹配算法HLM,进行提取并匹配线特征,并将端点转化为点特征,以完善特征点的丰富度,有利于拼接图像的对齐。

AX=0

(1)

其中：

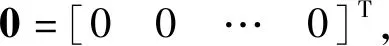
通过对式(1)的求解,即得到映射关系矩阵

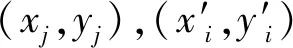
(2)

3 图像翘曲

图像翘曲过程中采用局部变形可以有效对齐拼接图像,传统算法采取矩形分割方法进行分块对齐,如图2所示,矩阵分割具有简单、易实现的特点,但刚性的图像分割破坏了内容的完整性,即：某些子图像中包含了多个平面的图像,这严重违背了单应性映射的条件(映射点对需要位于同平面),选取的网格中心点可能无法准确代表网格内多平面的内容,从而影响拼接图像的对齐。

图2 参考图矩形分割(50×50)

为解决传统矩形分割破坏图像完整性的问题,本文引入超像素算法对图像进行保护性分割。超像素算法分割图如图3所示。该算法是一种将图像中颜色、结构等相似且邻近的像素点分类在同一个像素小块中的分割算法,通过迭代,能得到代表所在像素块特性的最佳中心点,从而有利于拼接图像的对齐。

图3 参考图超像素分割

该算法首先将K个中心点均匀地分布在图像中,假设图片中像素点共有N个,则每个像素块的大小为Q=N/K;在种子点选取时步长为S=sqrt(Q),然后为周围的像素点找到所属的最佳中心点,每个初始小块的中心点为Nj=[lj,aj,bj,uj,vj]T,其中(l,a,b)表示在Lab颜色空间上,(u,v)表示空间坐标。本文分别从空间和颜色上衡量中心点与某一像素点Ni=[li,ai,bi,ui,vi]T的距离,如下所示：

(3)

(4)

(5)

式中：Ns是空间距离的最大值,Ns=S,Nc为颜色空间距离的最大值,Nc取固定值m,m∈[1,40]。根据距离公式,对图像中的像素点分类,单个像素块内的像素点通过迭代更新至收敛,得到新的中心点,最终得到超像素分割图像。

超像素分割算法将参考图分割成不同平面的子图像,并且获得各个子图像的中心点。通过式(6)获取映射关系。

(6)

对参考图的全局映射关系H*进行局部加权,以获得局部的映射关系h*,过程如下：

(7)

将参考图的每个中心点作为待匹配点x*,通过估计其与匹配点集的高斯距离,求出权重值。

(8)

其中γ∈[0,1],δ是尺度参数, 将式(7)进行加权处理,得到：

(9)

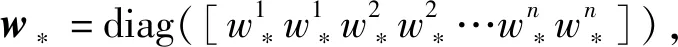
为进一步处理拼接图像的色差以及拼接缝问题,本文使用基于余弦函数的加权融合对图像进行融合,传统的线性加权平均融合算法具有简单、易实现的优点,但该算法减弱了图片的信息,使得过渡区拼接缝明显,图像融合效果不佳。本文采用平滑度更高的余弦函数权重进行平滑,如下所示：

(10)

(11)

f1+f2=1

(12)

(13)

式中：d表示重叠区像素点的列值;l表示重叠区的左边界所在列值;r表示右边界所在的列值。可看出,该平滑函数变化平滑,在重叠区的左半侧时,左边像素点权重增加,右边像素点权重减少,右半侧同理。余弦函数较平均加权函数更加的平滑,在重叠区两边能相应提高所在边的权重,具有更高效的融合效果[16]。

4 实验结果分析

本文实验在Windows 10(2.8 GHz CPU,8 GB RAM)系统上进行,使用MATLAB 2017和Visual Studio 2017结合Vlfeat 0.9.20和OpenCV库进行仿真。实验数据来源于文献公开数据集和本文采集的图像。分别从主观和客观方面,在35组实验中随机选取8组实验进行对比分析,以验证本文算法的有效性。

4.1 特征点分析

首先将SIFT+RANSAC和ORB+GMS两种传统特征点算法与本文算法进行特征点提取数量以及匹配效率方面的比较,不同算法特征点配准图实验结果如图4所示。

(a) SIFT+RANSAC (b) ORB+GMS

从图4(a)可看出,图中的特征点匹配对稀疏,特征丰富度不足,很多珍贵的内点未被提取,图4(b)中的特征点对数目较图4(a)有所提升,但特征点提取得不够全面,许多关键特征都未被有效提取。图4(c)中的单特征点与直线特征均被有效提取,与图4(a)、图4(b)比较,丰富度大大提高。将图4(c)中的线特征端点转化为点特征,得到图4(d),图4(d)中的特征点兼具丰富度与准确性,原因在于本文算法在单特征点基础上引入线特征以提高特征点丰富度的同时利用去重约束保证了准确性。不同算法的特征点匹配数和耗时如表1所示。

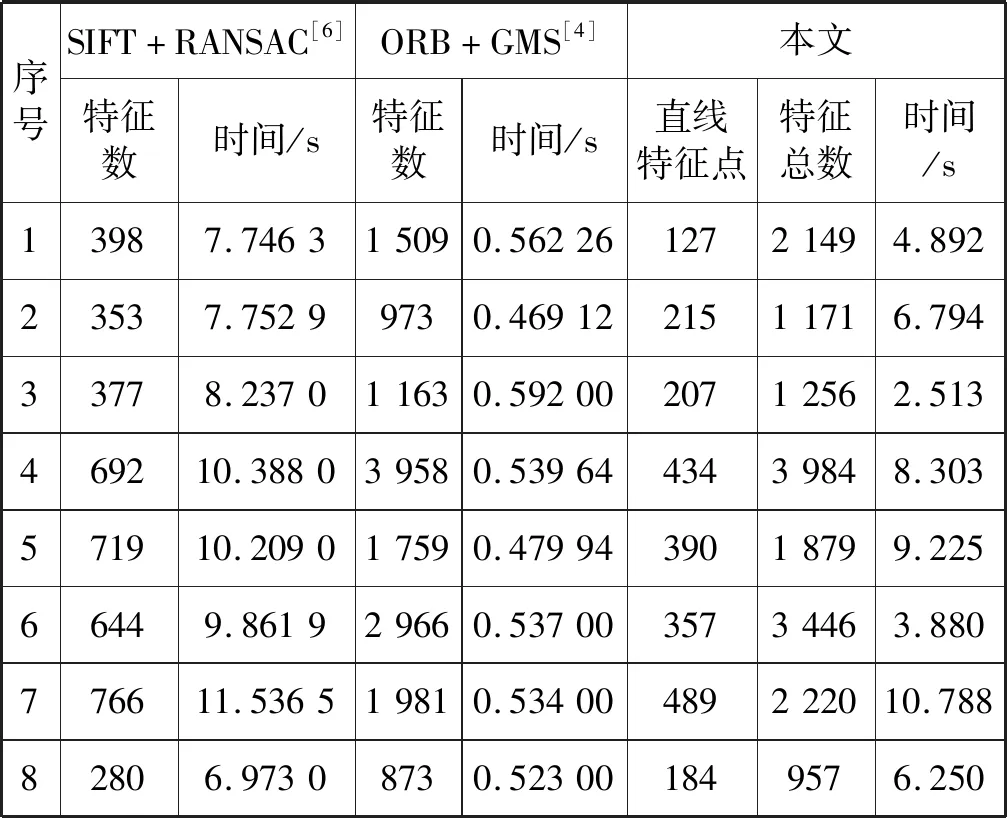
表1 不同算法的特征匹配数和时间比较

可以看出,在特征匹配数量方面,本文算法的特征匹配数为SIFT+RANSAC算法匹配数的2.61～5.39倍,较ORB+GMS算法,本文特征点总数平均值提高了14.513%,有效丰富了特征点数量。

在特征匹配效率方面,ORB+GMS算法匹配耗时少,SIFT+RANSAC算法和本文算法耗时较多。本文较SIFT+RANSAC算法,特征匹配耗时平均值缩短了28.241%,最终耗时位于两种算法之间。尽管ORB+GMS算法在效率方面有一定的优势,但其提取的特征不够全面,遗漏了许多关键特征点。本文在保证匹配效率的情况下,提高了特征匹配数量。综上,本文算法能有效丰富图像特征。

4.2 拼接图效果分析

为验证本文方法的有效性,在同等条件下,本文算法与APAP、AANAP、REW等算法进行实验比较。图5为不同算法的拼接图,图6为不同算法对应的局部放大图。

(a) APAP算法 (b) AANAP算法

(a) APAP算法 (b) AANAP算法

由图5可知,APAP、AANAP、REW算法的拼接图均出现不同程度的未对齐、重影等现象,本文算法的拼接图中物体能较好地对齐,视觉效果更好。从图6可知,APAP拼接图中书籍发生未对齐、塑料袋卷发生重影现象,图像失真严重;AANAP算法较APAP算法物体未对齐现象稍有缓解,但锯齿现象明显,且存在重影;REW算法较前两者拼接效果有所提高,但书籍拼接缝明显,塑料袋卷的重影问题仍未解决;本文算法得到的拼接图像更自然,拼接图像重叠部分的书籍纹理清晰,塑料袋卷得到有效对齐,消除了锯齿、重影和拼接缝明显等问题。

以上三种算法在特征点提取过程中,遗漏了珍贵的内点,使得翘曲不准确,影响拼接效果。在翘曲过程中,三种算法均使用了规则的网格划分模型,图像在分割过程中边界以及周围相似特征点没有划分在同一个区域块中,选取的中心点可能同时包含多个平面,从而影响单应性的准确性,导致拼接效果不佳。本文提出的基于点线配准和超像素分割的图像拼接算法,线特征点的加入,有效地丰富了特征点,并引入超像素算法实现图像内容保护划分和单应性的准确计算;有效解决了因图像视差引起的拼接图像变形、错位、重影以及拼接缝明显等问题,得到更自然、视觉效果更好的拼接图像。

仅通过主观评价不足以验证本文算法的有效性,本文选取与人眼主观评价一致性更高的NIQE算法对不同算法的拼接效果进行对比[17]。不同算法的NIQE值对比如表2所示。

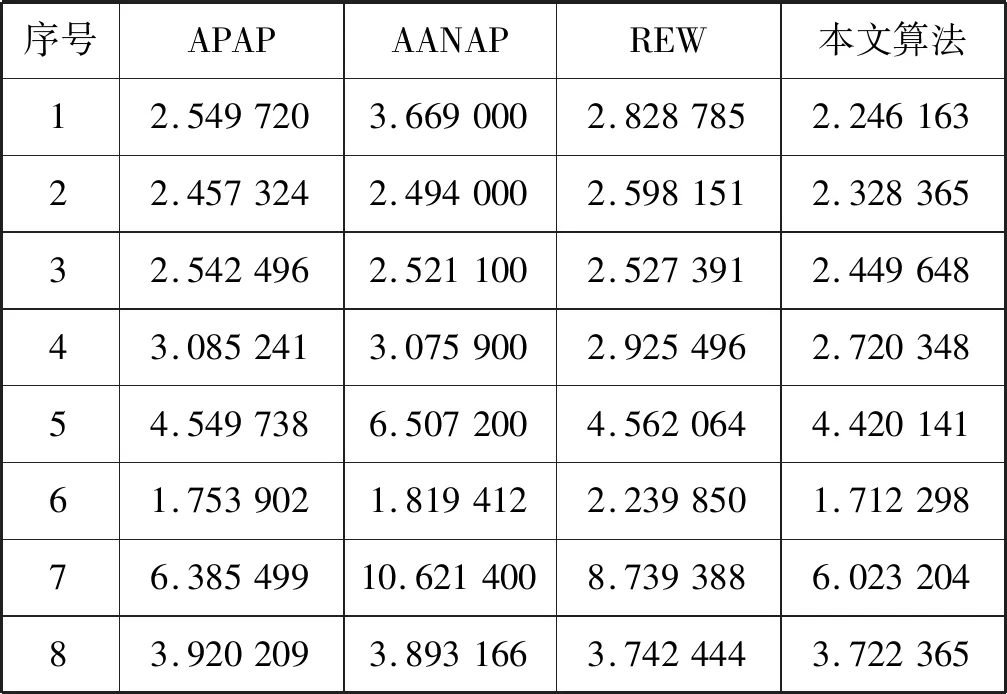
表2 不同算法的NIQE值比较

从表2可知,本文的客观评价指标值NIQE均小于APAP、AANAP及REW算法,较APAP算法NIQE值低了0.04～0.36,较AANAP算法NIQE值低了0.071～4.598,较REW算法NIQE值低了0.02～2.71。这说明本文算法得到的拼接图与原图更接近,质量更高。通过多组实验验证了本文算法的优越性和有效性。

5 结 语

针对目前图像拼接中出现的图像错位、重影等问题,经典的拼接算法均采用单特征点结合图像矩形分割的方法,拼接图中存在的问题未得到有效解决。本文首先在单特征点基础上引入直线特征,以丰富图像特征点,并使用映射关系和去重约束,确保特征点的准确性;然后利用超像素分割模型代替传统的网格划分,使得图像分割块具有内容完整性,得到更准确的分块中心点,提高了拼接图像的对齐精度。结果表明,本文提出的基于点线配准和超像素分割的图像拼接算法,无论是在主观视觉上还是客观评价指标上均优于对比算法,有效解决了因图像视差引起的拼接图错位、变形等问题。