基于似然估计修正信噪比的编码调制切换算法

刘庆利 王美恩

(大连大学通信与网络重点实验室 辽宁 大连 116622)

0 引 言

随着当今卫星通信技术的发展,其较强的应用价值体现在了多个方面,作为信息化时代发展的重要支撑手段与技术,发展速度越来越快,应用范围也越来越广[1]。空间数据系统咨询委员会(Consultive Committee for Space Data System,CCSDS)研发了高级在轨系统(Advanced Orbiting System,AOS)[2-5]。然而卫星通信受外部环境的影响较为严重,因此,自适应编码调制(Adaptive Coding and Modulation,ACM)被广泛引入来优化通信链路。目前,ACM技术的研究主要集中在模式选择方法[6-7]、信道编码改进、信道状态信息(Channel State Information,CSI)精确捕获和ACM实现。其中,调制与编码策略(Modulation and Coding Scheme,MCS)的选择是ACM技术的核心部分。为了确保链路中信息传输的可靠性和及时性,可以选择信噪比(Signal-to-Noise Ratio,SNR)作为CSI的衡量指标,选择满足特定要求的调制、编码和数据速率最终形成特定的MCS类型的组合,并充分利用可用的通信信道资源使MCS类型和数据传输速率适应无线环境条件[8-9]。目前存在三种常用MCS切换算法：基于最小SNR的MCS(MCS Based on Minimum SNR,M-MCS)切换算法虽然保证了误码率但极大地牺牲了系统的吞吐量,基于平均SNR的MCS(MCS Based on Average SNR,A-MCS)切换算法则牺牲误码率来保证吞吐量,基于方差修正平均SNR的MCS(MCS Based on Variance SNR,V-MCS)切换算法采取折中方式但不适合时变衰落信道。

近年来,为了提升通信效率,国内外学者对MCS切换进行了深入的探究,文献[10]根据M-MCS、A-MCS和V-MCS这三种算法的切换过程,通过仿真优选出系统的数据传输最佳概率值,提出基于概率估计的MCS切换算法,该算法在一定程度上提升了系统的吞吐量,但是算法的计算过程复杂,复杂度较高。文献[11]对SNR的方差进行修正,提出一种基于经验方差修正SNR的MCS(MCS Based on Empirical Variance SNR,EV-MCS)切换算法。该算法能在提升系统的吞吐量同时降低算法的复杂度,然而该算法修正的方差是一种经验值,通过不断修正方差系数得到,会增大MCS切换算法受参考SNR和判决门限的误差。针对以上问题,本文提出一种基于似然估计修正SNR(MCS Based On Likelihood Estimation SNR,LE-MCS)的MCS切换算法,在V-MCS切换算法的基础上,考虑了时变衰落信道对数据传输的影响,同时结合最大似然估计方法和长短期记忆神经网络来匹配发射端的参考SNR和降低系统发射端获取SNR的时延,可以在提升系统传输效率和吞吐量的同时降低系统的误码率。

1 ACM相关技术

对于AOS通信系统,数据在系统的发送端进行缓存,根据接收端反馈的信道信息进行ACM,然后在经过时变衰落信道到达接收端,由于外部环境和信道的影响,若接收端在校验时发现错误,就通过反馈信道向发送端发送重传请求,通信系统发送端的HARQ机制就会重传数据。AOS通信系统如图1所示。

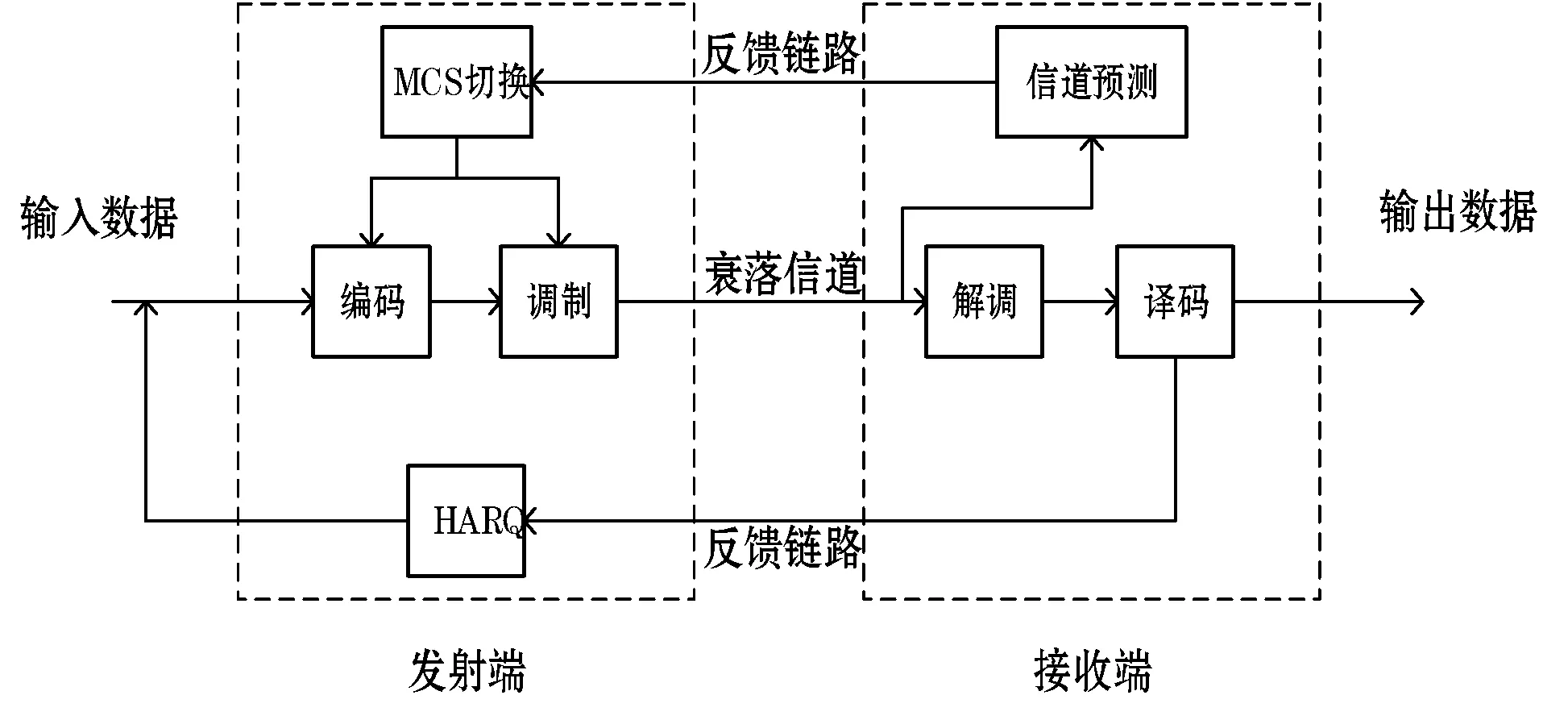
图1 AOS通信系统框图

对于AOS通信系统而言,传输数据在发送端通过不同的信道编码和调制方式进行调整,而不同编码策略和调制方式的组合可以为AOS通信系统的信息传输提供不同的性能。不同的调制方式可以在不同的环境下提高系统的频带利用率,不同的编码方式以及编码速率能够保证系统在不同环境下的误码率。然而,高阶数调制和高编码速率能够提高系统的传输效率,却不能保证系统的误码率;低阶数调制和编码虽然保证系统的误码率,却大大地损失了系统的传输效率。因此,需要通过MCS切换进而实现最佳的传输效益。

2 MCS切换算法及改进

2.1 编码与调制策略的选择

MCS选择的一种分析方法基于以下参数：误码率(BER)和通信系统信道的信噪比(SNR)。优选的MCS类型是提供最高系统性能或等效地以可接受的可靠性提供最高数据传输速率的类型[12]。在MCS的切换算法中,如何依据发射端的参考SNR来匹配MCS切换策略是MCS切换的核心问题。

第二代传输标准为ACM技术提供了28种MCS,其中有四种MCS的误码率低于0 dB,不适用于无线信道传输[13]。由于不同的编码速率和调制解调方式在传输过程中的不同效果,本文选取其中三种较为典型的MCS在AWGN下的吞吐量和误码率进行仿真测试,则仿真效果如图2所示。

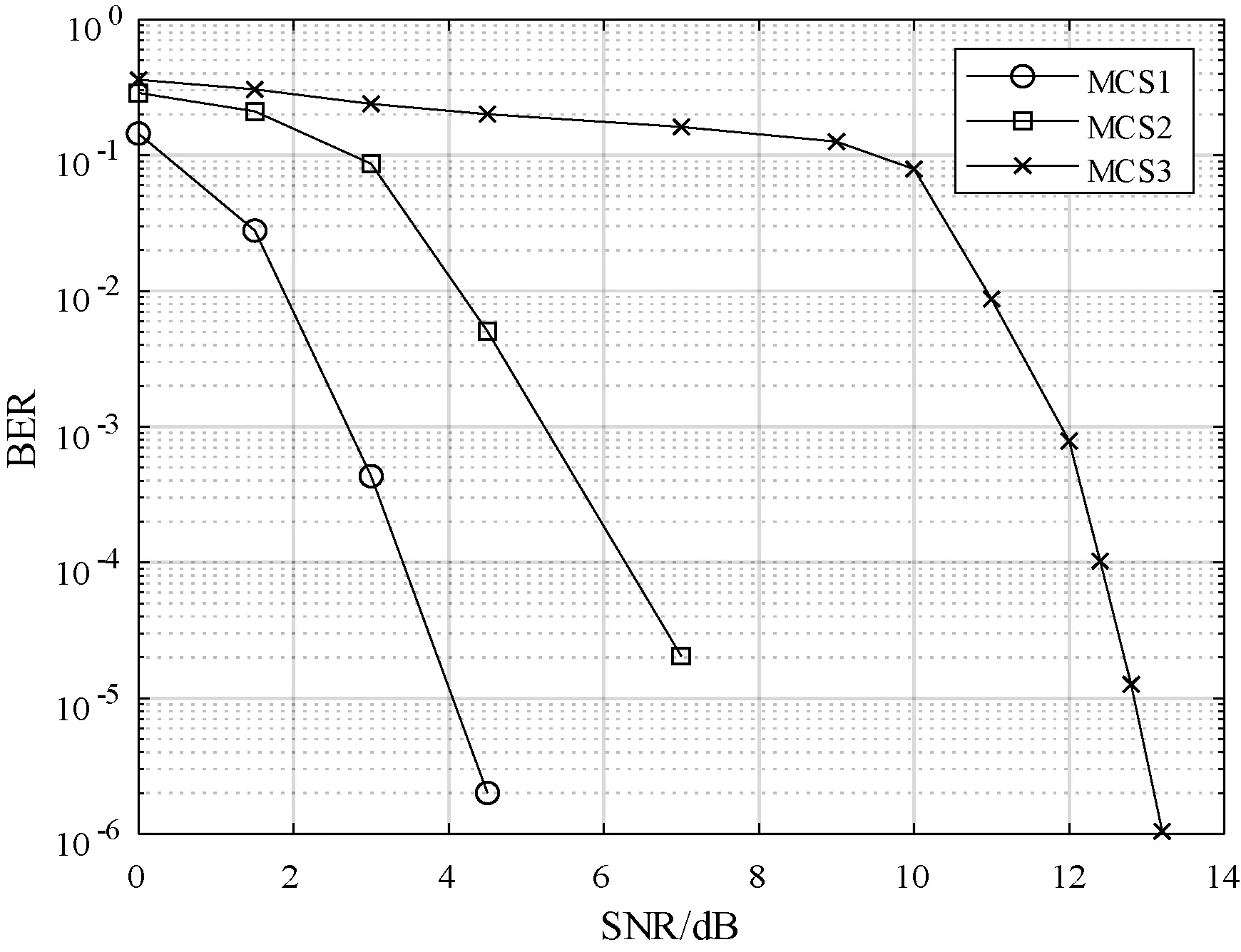
图2 三种MCS在AWGN下误码率仿真结果

本文假设系统的目标误码率为10-4,则由图2可以得出所选的三种MCS在达到目标误码率的切换界限,它们的切换策略、切换门限、吞吐量如表1所示。

表1 系统选取MCS策略

在传统神经网络中,模型不会关注上一时刻的处理会有什么信息可以用于下一时刻,每一次都只会关注当前时刻的处理,而循环递归神经网络(Recurrent Neural Networks,RNN)虽然带有记忆功能但却存在梯度消失或爆炸的缺陷,不适用长期依赖的问题,而长短期记忆网络(Long Short-Term Memory,LSTM)在RNN的基础上改进了门结构和记忆单元,使得LSTM可以更好地处理长时依赖问题。在传统的MCS切换算法中,信道SNR的捕捉一般通过系统的接收端进行信道估计再反馈给系统的发射端来完成,但采用这种方法会因为卫星通信链路距离较长而无法避免通信时延增大的问题,故本文采用LSTM克服信道长时依赖的问题。

在本文中,MCS的切换采用固定门限法,以BCH、RS、LDPC码为编解码策略,以QPSK、QAM作为调制解调方案,系统MCS的切换以AOS发送端的参考SNR为标准,而参考SNR由信道状态信息CSI决定,通过LSTM来预测信道的SNR并反馈给系统的发射端。

2.2 LSTM预测SNR

卫星通信的信道受到大尺度衰落和小尺度衰落的影响,且卫星沿着轨道进行高速运动,导致卫星与终端间的信道不断发生变化[14],在系统的数据传输过程中,为了获得更多的吞吐量,提升系统的通信质量,卫星通信链路通常会需要进行实时的信息交互,以获取准确的信道状态信息,然而由于通信链路的较大时延会导致测量的CSI与实时的信道状态存在延迟进而造成反馈误差,影响通信质量。

本文首先根据卫星和通信信道的信道模型,获取通信链路建立连接的信道的SNR,并将其作为长短期记忆网络LSTM的输入,通过模型的训练,预测链路通信期间的任意时刻的SNR,进而解决了信道估计在反馈时的时延误差的问题,系统的发送端可以根据SNR的预测值实时调整MCS,以更快地适应信道的变化,提升系统的吞吐量。

卫星通信链路在自由空间的传播损耗可表示为：

(1)

式中：Pt和Pr分别表示为通信系统的发射功率和接收功率;Gt和Gr分别是系统发射端和接收端的天线增益;d为通信链路的通信距离;f为工作频率;c为电磁传播速度。由式(1)可知,当工作频率f固定时,通信的传播损耗主要与通信距离d有关,通信距离越长,则传播损耗越大。

在自由传播损耗的基础上,通信链路的SNR计算公式如下：

γSNR=Pt+Gt+Gr-Lp-Lf-Ag-kbBTe

(2)

式中：Lp是降雨衰减;Ag是大气吸收损耗;kb是玻尔兹曼常数;Te是噪声温度;B是信道带宽。

本文采用自适应编码调制方案ACM,根据信道状态实时地切换MCS策略来适应信道的变化,理想情况下的信道的吞吐量如下：

(3)

式中：Tt为通信时长。

LSTM的网络结构如图3所示。

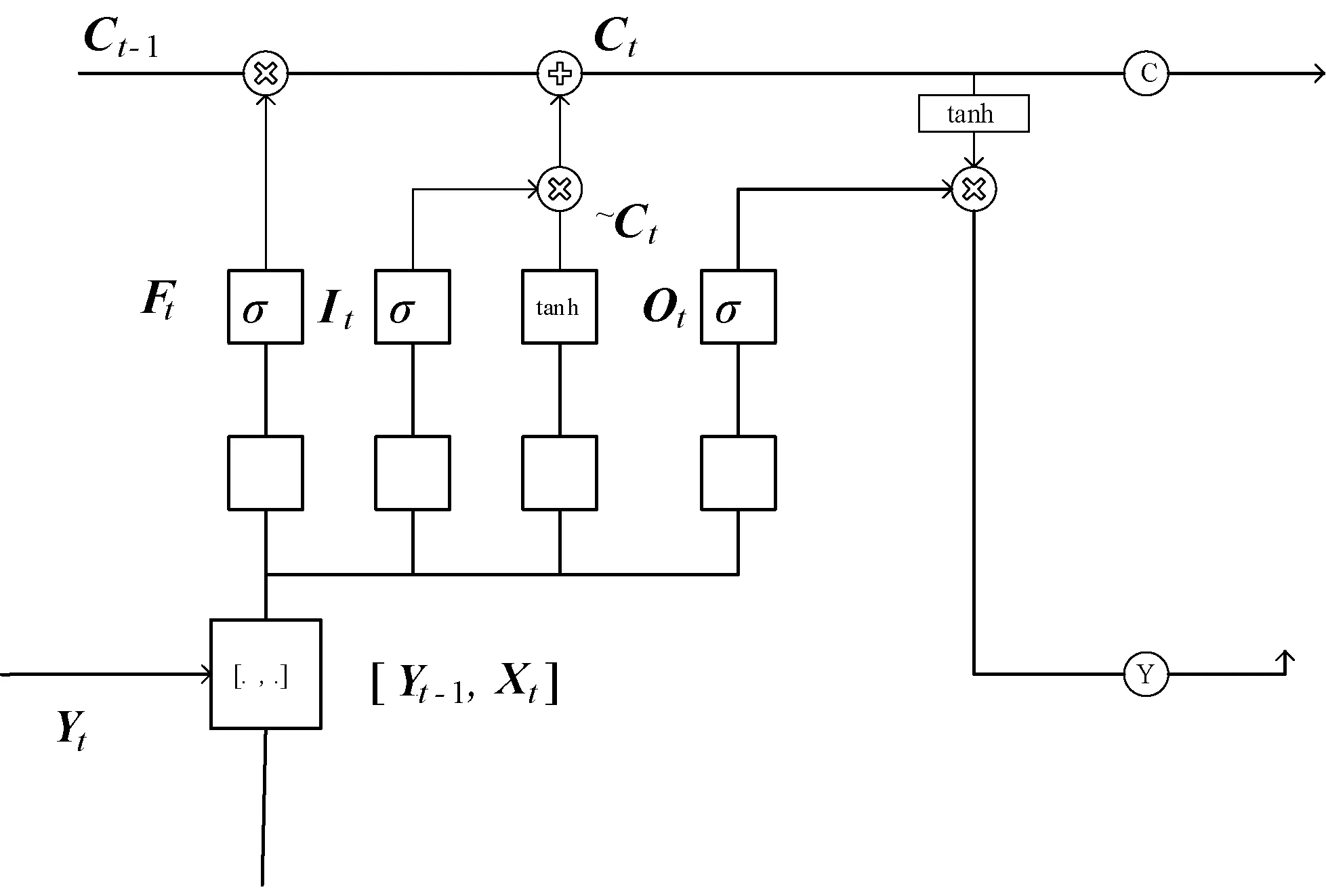
图3 LSTM网络结构

LSTM网络对遗忘门、输入门、单元状态、输出门、单元输出[15]的定义分别如式(4)-式(8)所示。

Ft=σ(WF[Yt-1,Xt]+BF)

(4)

It=σ(WI[Yt-1,Xt]+BI)

(5)

(6)

Ot=σ(Wo[Yt-1,Xt]+BO)

(7)

Yt=Ot⊙tanh(Ct)

(8)

式中：X表示输入数据;Y表示输出;C表示记忆单元值;⊙表示矩阵元素相乘;σ为Sigmoid函数。LTSM首先进行前向传播并计算上述式子的五个向量值,然后反向传播计算每个预测神经元的误差项,最后根据误差项计算出新的权重参数。

在通信链路进行数据传输前,地面终端与卫星网络建立信息连接交互,因此,可以将连接过程中获取的SNR作为LSTM网络的输入,通过LSTM的训练,预测下一时刻的信道的SNR,并将此SNR作为输入,继续预测下一时刻的信道信息,以此类推,预测出通信期间的CSI。本文选取的LSTM模型通过Python的Keras模块进行搭建、编译。

2.3 MCS切换过程

假设参考的SNR为γi,根据编码和调制方式的不同将SNR区间划分为不同的对应的区间Ti,则编码调制的方案具体如式(9)所示。

(9)

在划分SNR的区间Ti时,若SNR切换门限过高,对于接收SNR较低的符号就会造成误码;SNR切换门限过低,对于接收SNR较高的符号又会牺牲它们对应的吞吐量,因此必须根据不同的MCS设计合适的SNR区间。

V-MCS切换算法是针对选取码块中各符号接收SNR的平均值,用传输符号的方差σr进行适当修正,假设在一个码块周期内的传输符号数为N,各传输符号的接收SNR为γn,发送端在得到信道估计值之后,其修正方式如式(10)所示。

γt=μn-σr

(10)

式中：μn是传输符号对应的SNR的均值;σr是传输符号对应的SNR的方差;γn代表传输符号的对应的SNR,它是通过信道估计反馈给系统的发射端。σr和μn分别计算如下：

M-MCS切换算法能够完全保证系统的误码率低于目标误码率,但是会极大地牺牲吞吐量性能;A-MCS切换算法能够有效提高系统吞吐量性能,但是不能保证系统的误码率低于目标误码率。

2.4 基于似然估计修正SNR的MCS切换

V-MCS切换算法虽然对吞吐量和误码率进行了折中,但它并没有综合考虑到时变衰落信道对数据传输造成的影响,所以并没有达到最优的状态,这种切换算法仍然可以继续优化。极大似然估计提供了一种给定观察数据来评估模型参数的方法[16]。由于信道的衰落值符合高斯分布,因此在发射功率恒定的情况下,信道的信噪比的概率特性可以近似呈正态分布[17],如图4所示。

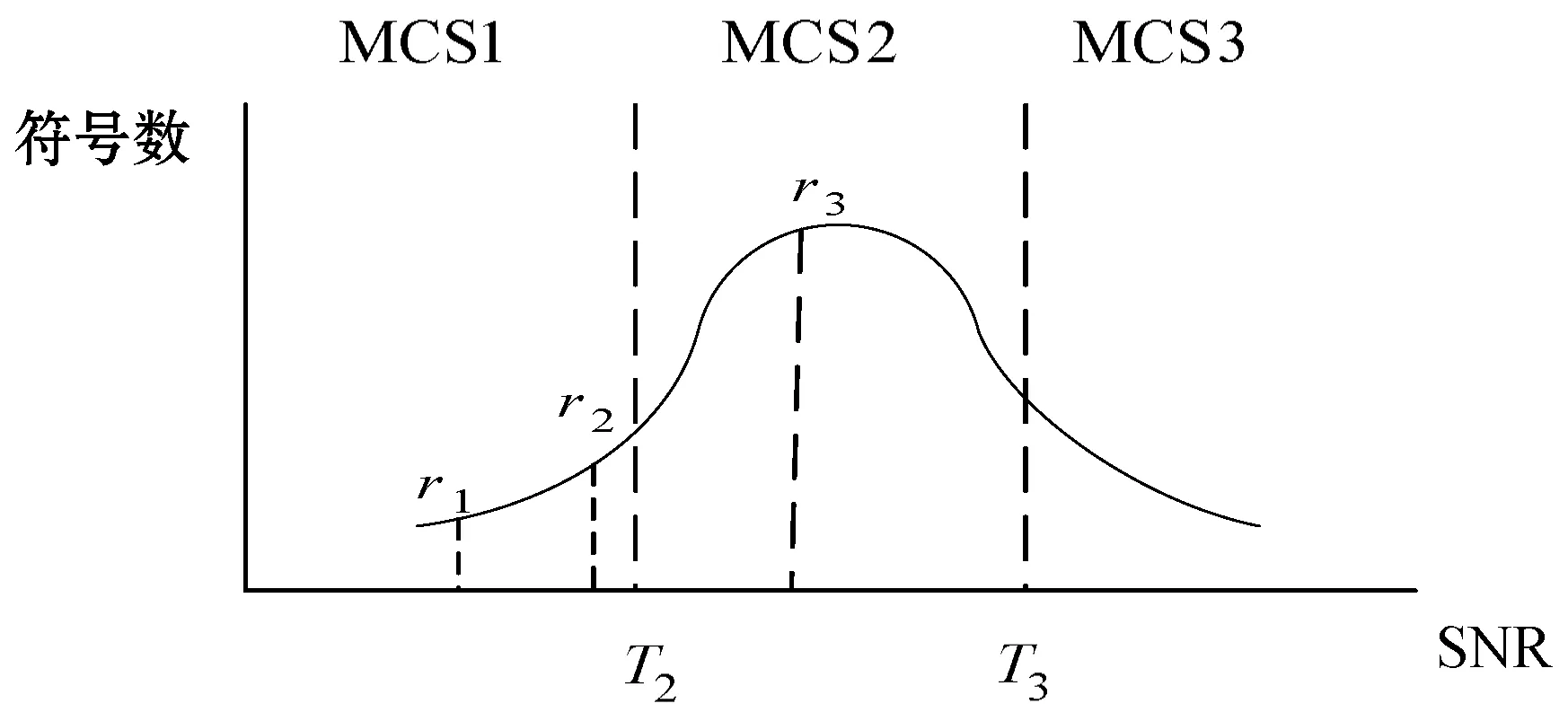
图4 三种MCS切换算法的参考SNR

T2和T3是MCS2和MCS3的切换门限,r1、r2、r3分别代表着M-MCS切换算法、A-MCS切换算法、V-MCS切换算法的参考SNR。由图4可以看出M-MCS切换算法的传输符号在码块周期内的SNR都大于r1,即使这些符号应该采用MCS2、MCS3或更高阶的编码调制方式,然而由于r1的作用而选择了MCS1。所以M-MCS切换算法能保证误码率但极大地损失了吞吐量。A-MCS切换算法参考SNR落在正态分布的中点位置,那么T2左侧的符号本应该采用MCS1却选择了MCS2,就会造成误码。若左侧符号越多,则误码率就越高。V-MCS切换算法用传输符号的接收SNR的方差来对均值进行修正,使参考SNR贴近切换门限,同时考虑了传输符号的误码率和吞吐量。

然而,由图4可以看出,虽然V-MCS切换算法的参考SNR更贴近切换门限,但在传输符号的MCS的选择上仍然存在一定的误差。设想V-MCS切换算法对A-MCS切换算法的均值修正过度导致V-MCS切换算法没有达到理想效果。

由于AOS通信系统数据的传输受天气、多径效应和时变衰落信道的影响,因此,信号中的各个符号的衰减也各不相同,导致每个符号在接收端的SNR也不同。由此,针对V-MCS切换算法的改进可以分为两个部分,其中一个部分是考虑到每个符号的不同衰减,改变方差的修正系数。具体方法是将式(10)改进为式(11),在原来的方差修正的基础上考虑修正系数f的影响。式(11)是改进后的参考SNR的表达式。

γt1=μr-f·σr

(11)

式中：f代表方差修正系数;μr和σr分别对应V-MCS中传输符号对应SNR的均值和方差。LE-MCS中γn经过LSTM的预测并反馈给系统的发射端,根据各个传输符号的γn由于时变衰落信道和外部环境的影响会不断变化,求解各个传输符号在信道影响下的不同的权重f1,然后取不同权重的均值作为该信道对于符号的影响即修正系数f,它们的表达式如下：

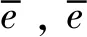
(12)

(13)

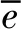
D={r1,r2,…,rn}

(14)

(15)

(16)

算法的流程如图5所示。

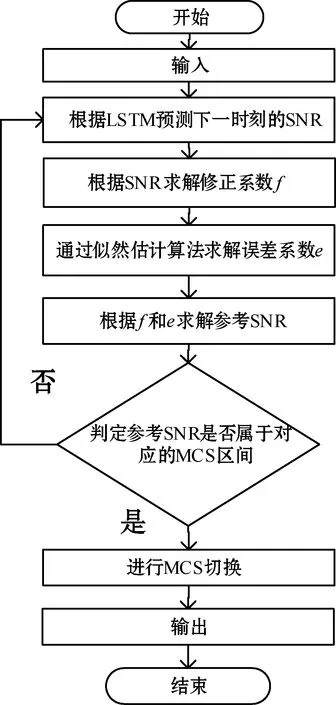
图5 算法流程

LE-MCS切换算法可以分为以下步骤：

(1) 通过LSTM预测出下一个时刻的SNR。

(2) 将γn反馈给系统的发射端。

(3) 由γn求解修正系数f。

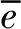
(6) 通过参考SNR进行MCS区间的判决,若属于对应的MCS区间,则进行对应的MCS切换,否则,回到步骤(1)重新预测。

3 仿真验证及分析

本文通过MATLAB仿真了LE-MCS切换算法的性能,仿真实验中主要以AOS通信系统数据传输的传输效率、吞吐量和误码率为测量指标,为了简化实验过程,采用加性高斯白噪声信道(AWGN),信道编码选用RS码、BCH码、LDPC码,调制方式选用QPSK、16QAM、64QAM,构成三种MCS选择策略。由于M-MCS和A-MCS的吞吐量和误码率太低,在实际通信中很少采用,而V-MCS是在M-MCS和A-MCS的基础上改动,LE-MCS又是根据V-MCS改进而来,故本文只需对比LE-MCS切换算法、V-MCS切换算法和EV-MCS切换算法这三种算法的仿真效果。

3.1 仿真参数设置

本文在AWGN信道下,选取三种MCS策略,在[0,15]的SNR区间内模拟LE-MCS、EV-MCS、V-MCS的切换过程,具体仿真参数如表2所示。

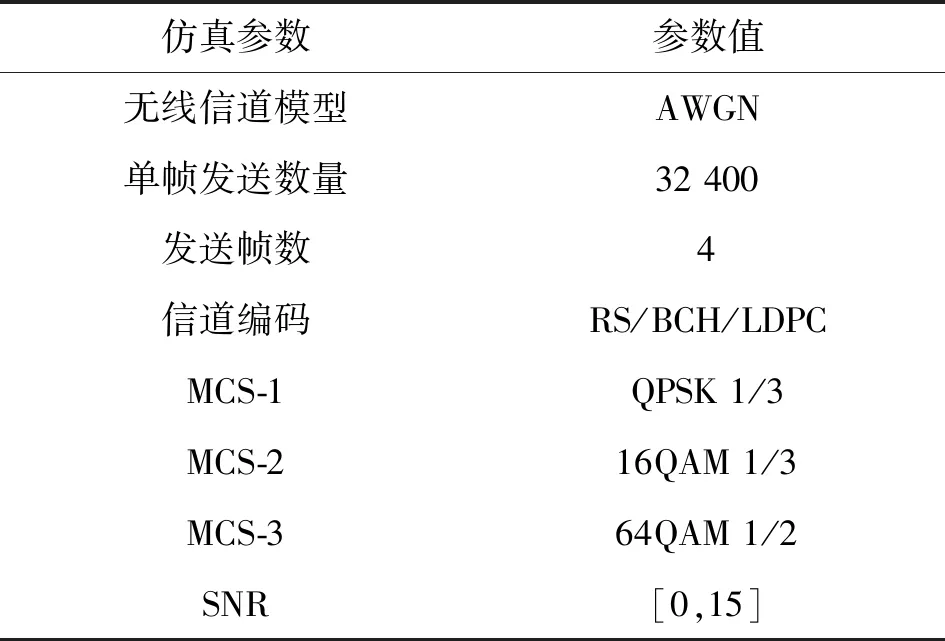
表2 仿真参数设置

3.2 仿真结果分析

图6和图7分别是三种MCS切换算法的传输效率和吞吐量的对比。

图6 传输效率对比

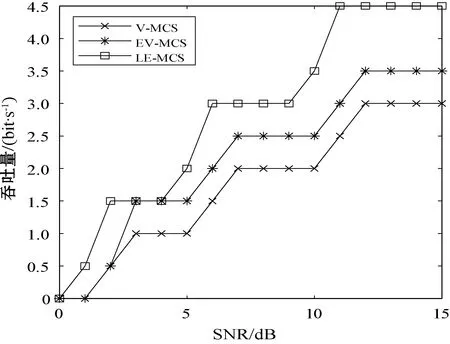
图7 吞吐量对比

由图6可以发现,随着信道状况的改善,三种MCS切换算法都能逐步提升系统的传输效率,但是整体上,LE-MCS切换算法提升效果相较于其余两种MCS切换算法更明显,LE-MCS切换算法的传输效率相比于EV-MCS提升了10%,相较于V-MCS提升了20%。

由图7可以发现,三种MCS切换算法在整体趋势上呈现阶梯式上升,表明每种MCS策略提升系统吞吐量的能力有限,当到达该极限时,系统的吞吐量就展现出稳定的趋势,然后随着信道的改善,系统切换到另一种MCS继续提升系统的吞吐量,但是,总体上三种MCS切换算法都能提升系统的吞吐量。在SNR小于1时,此时的信道条件很差,系统数据的传输能力也很低,故此时的三种算法的吞吐量都很差。但是,随着信道条件的逐步改善,三种MCS切换算法的差距开始逐渐展现,其中：LE-MCS切换算法提升系统吞吐量的能力最强,其次是EV-MCS切换算法,最后是V-MCS切换算法。同时,LE-MCS切换算法的切换门限要低于其他两种切换算法,表示LE-MCS切换算法可以更灵敏地捕捉信道变化并进入MCS的切换过程,表明LE-MCS切换算法在提升系统吞吐量的同时也提高了系统切换的灵敏度。

由图8可以发现,最初由于信道条件太差,数据传输的误码率很高,三种切换算法都选择了低阶的编码调制方式来保证数据的传输,故此时三种切换算法的曲线大致相同,随着信道条件的逐步改善,三种切换算法开始逐渐进行编码调制的切换,因此,三种切换算法的误码率总体趋势相似,而三种切换算法中,LE-MCS切换算法的误码率最低,其次则是EV-MCS切换算法的误码率,最后V-MCS切换算法的误码率最高。同时,误码率曲线并不连续,不连续的地方表示此刻系统从低阶MCS切换到高阶MCS,但刚刚切换到高阶时,SNR相对于高阶MCS较小导致误码率升高,随着SNR的升高,误码率会逐渐降低,因此出现分段现象。

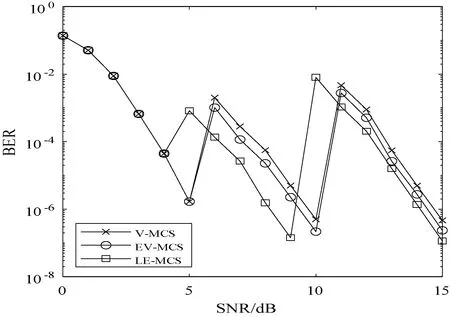
图8 误码率对比

综合上述可以发现,LE-MCS切换算法可以在保障系统的误码率的同时提升系统的传输效率和吞吐量。

4 结 语

本文针对传统的MCS切换算法不能同时满足通信系统数据传输的传输效率和误码率的缺陷,以提升AOS通信系统数据传输效益为准则,提出一种LE-MCS切换算法。首先根据时变衰落信道对各个传输符号的不同时刻的影响求解各个符号在信道影响下的权重,然后取权重的均值作为信道对传输符号的影响,同时根据SNR的概率特性,结合最大似然估计算法和LSTM,最后通过两者联合求解改进切换算法后的参考SNR,然后结合门限法匹配到MCS的切换区间从而完成MCS的切换。仿真结果表明,LE-MCS切换算法在保证系统的误码率的同时提升系统的传输效率和吞吐量,改善了通信系统的传输效益。