基于预瞄的模糊自适应路径跟踪算法研究

刘长伟，汤庆涛，王金桥，高 洁，白彦梅，王新树

（奇瑞新能源汽车股份有限公司，安徽 芜湖 241000）

0 引 言

路径跟踪是智能汽车控制的关键技术，目前主要方法有PID （Proportional-Integral-Derivative，比例、积分和微分）控制、模糊控制、神经网络控制、MPC（Model Predictive Control，模型预测控制）以及传感器信息融合算法等。江浩斌[1]根据不同车速和道路曲率，利用遗传算法优化得到一种所有典型弯道工况下时域参数自适应的MPC 路径跟踪控制器。杨琛[2]基于遗传算法优化PID 控制器提出一种路径跟踪控制方案，建立状态空间型无人艇运动数学模型以及随机干扰数学模型，在传统LOS （Line-of-Sight，视线制导）算法中引入积分项，实时补偿航向漂角干扰，以减小横向误差。梁艺潇[3]利用汽车动力学模型求解自适应率，通过车辆-路径联合模型，基于LQR（Linear Quadratic Regulator，线性二次型调节器）求解各顶点子模型处的反馈控制律，提出一种基于多模型自适应方法的智能汽车路径跟踪控制。张炳力[4]利用神经网络自学习和自调整特性，结合模糊控制，设计一种轨迹跟踪控制器。

本文基于预瞄理论提出一种基于模糊控制的自适应前视距离纯追踪模型的路径跟踪方法。纯追踪模型利用几何方法模拟驾驶时情况，所用参数较少，具有一定预见性，但确定前视距离较困难，可通过模糊控制自适应调整前视距离来解决，从而确定智能汽车路径跟踪时期望的转向角度。

1 数学建模

设计导航算法时，简化车辆数学模型，得到车辆横向运动学二轮简化模型[5]，如图1 所示，将车辆左右车轮重叠为仅有前后车轮，其中车辆前轮坐标为（xq，yq），后轮坐标为（x，y），θ为车辆航向角，δ为车辆前轮转角，L为车辆轴距，v为车辆行驶速度。

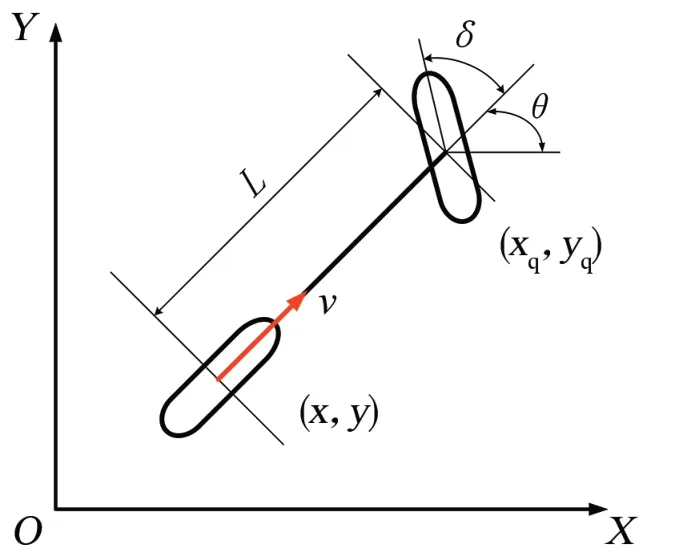
图1 车辆运动学二轮模型

由图1可得如下各式。

式中：x′为后轮横坐标对时间的导数；y′为后轮纵坐标对时间的导数；x′q为前轮横坐标对时间的导数；y′q为前轮纵坐标对时间的导数。

根据式（1）～（3）可得

即

式中：θ′为车辆航向角对时间的导数；t为时间。

由于车辆后轮受到非完整性限制[6]，则式（4）满足x′= cosθ，y′= sinθ或者成倍数关系，所以当车辆以速度v行驶时，x′和y′可表示为

由式（7）～（9）得

综上，车辆横向运动学模型为

式（11）适用于车辆低速行驶工况，并且不考虑轮胎侧滑等影响，采用此模型解决车辆自动导航时的路径跟踪问题。

2 模糊自适应纯追踪算法

2.1 纯追踪算法

根据几何关系建立转向角度与转弯半径间关系，在当前位置点和预定路径上的预瞄点间规划一条圆弧，计算车轮的转向角度，如图2所示。

图2 纯追踪模型原理

将车辆行驶简化为二维运动，图2中预定路径上的预瞄点坐标为（a，b），Lq为车辆当前位置与预瞄点间弧的弦长，即前视距离，R为圆弧的曲率半径，Pe为车辆与预定路径的横向偏差，θe为车辆当前航向与预定路径航向之间的角度偏差，即航向偏差。

由图2可得如下各式。

联立式（12）～（14）得

根据文献[7]得到a的计算式为

同时由阿克曼转向原理[8]得

式中：L为轴距，δ为前轮转角。

将式（16）代入式（15）、（17）得

由式（18）可知，为确定前轮转角δ需确定前视距离Lq，Lq决定跟踪精度。如果Lq较大，则跟踪行驶的路径曲率较小，跟踪轨迹较平滑，但控制响应时间较长；如果Lq较小，则跟踪行驶的路径曲率较大，虽然此时控制响应时间很短，但会产生较大振荡。有学者将Lq视为关于速度的函数，相关参数包括车速、最小转弯半径、最大制动加速度等，通过计算得到固定的Lq，但由此得到的不同路径下的跟踪效果差别很大。车辆行驶中，当横向偏差和航向偏差较大时，前视距离Lq较小，此时可迅速减小误差；相反，如果横向偏差和航向偏差较小，则Lq较大。

2.2 模糊控制算法

目前模糊控制应用越来越广泛，将实践经验转化为模糊控制规则，在模糊控制器中对控制参数进行模糊化处理，并将处理结果输入执行机构[9-10]。

模糊控制系统主要由模糊化、模糊推理、清晰化、规则库、控制对象5部分组成，其中模糊化、模糊推理、清晰化、规则库构成模糊控制器[11]，如图3所示。

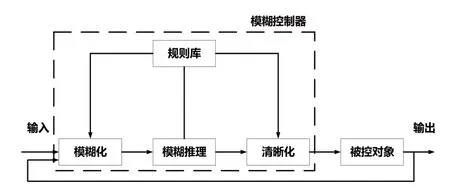
图3 模糊控制原理

3 路径跟踪仿真

本文采用一种改进的基于模糊自适应前视距离的智能车路径跟踪方法，对纯追踪模型中的前视距离进行实时调整，根据实时不同航向偏差和横向偏差确定前视距离和前轮转角，如图4所示。

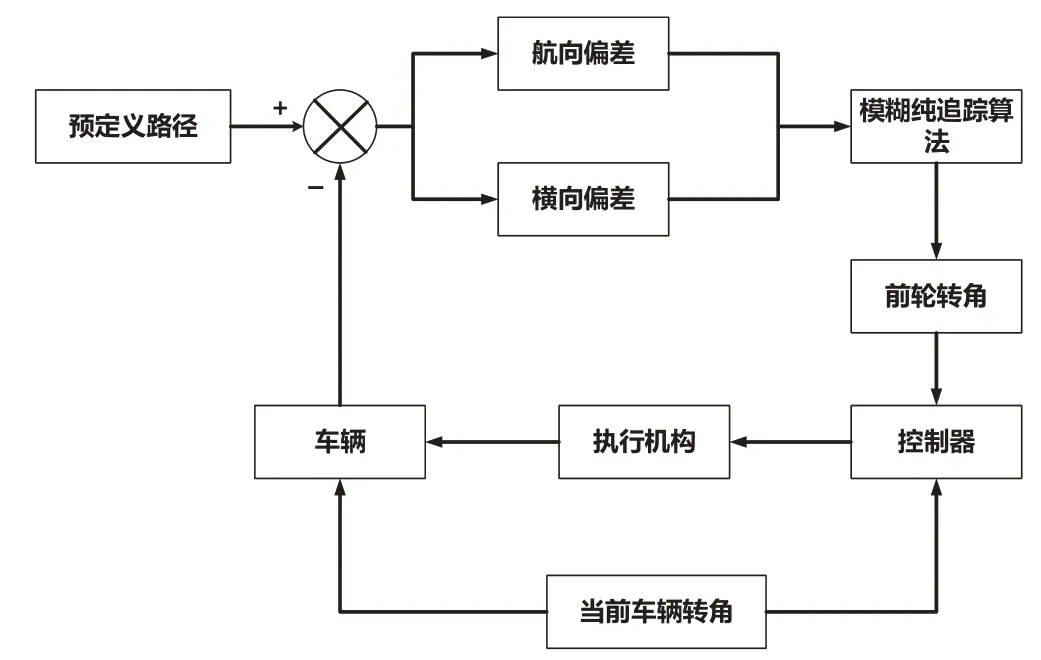
图4 模糊自适应路径跟踪原理

3.1 变量模糊化

模糊控制中输入和输出变量的个数可以是一个也可以是多个，通常输出变量越多则控制越复杂，控制精度也越高。本文采用二维模糊控制器，即有两个输入参数：车辆横向偏差Pe和航向偏差θe，前视距离Lq为输出变量。

1）横向偏差Pe模糊化

在MATLAB 模糊控制模块中设定Pe基本论域为[-100，100]，单位为cm；量化等级为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，量化因子为6/100=3/50，如图5所示。

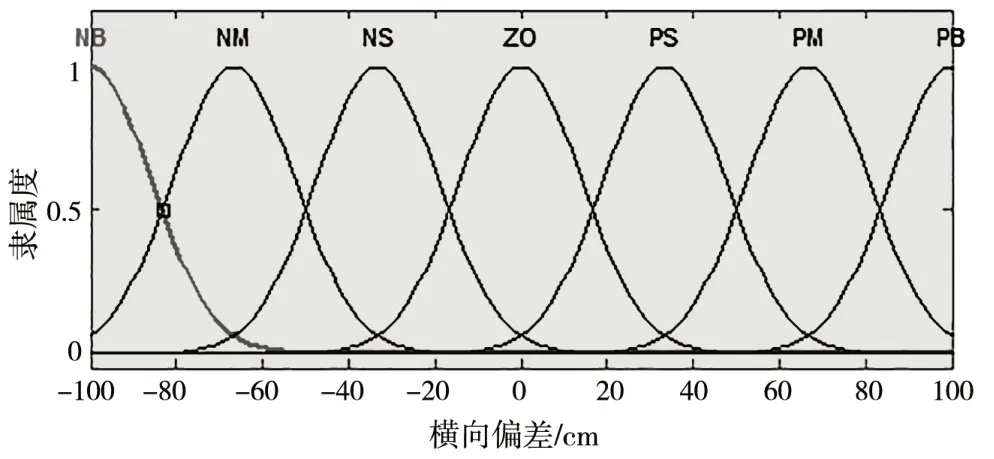
图5 横向偏差Pe隶度函数

2）航向偏差θe模糊化

在MATLAB 模糊控制模块中设定θe基本论域为[-90，90]，单位为 °；量化等级为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，量化因子为6/90=1/15，如图6所示。

图6 航向偏差θe隶度函数

3）前视距离Lq模糊化

在MATLAB 模糊控制模块中设定Lq基本论域为[0，800]，单位为cm；量化等级为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，量化因子为6/800=3/400，如图7所示。

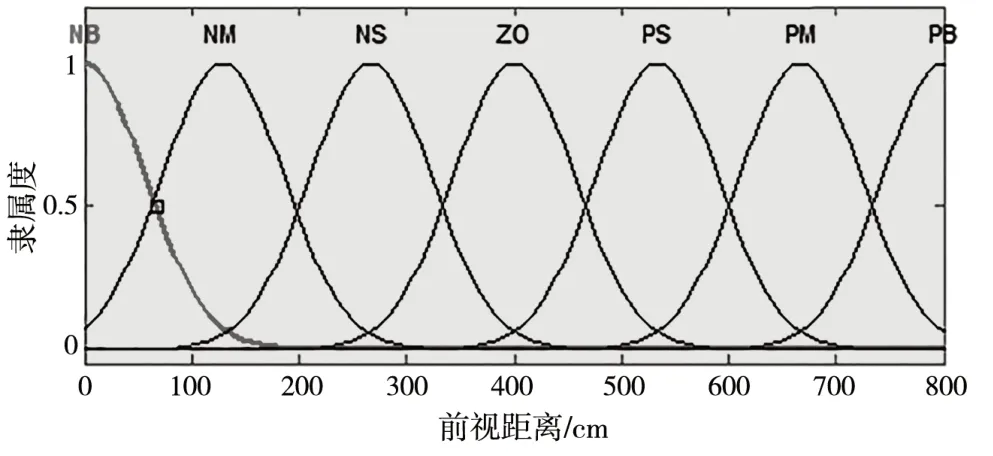
图7 前视距离Lq隶度函数

3.2 模糊推理规则

对于输入、输出变量采用定性词语“大、中、小”进行描述，并且由于每个变量均会出现正、负和零，则采用负大、负中、负小、零、正小、正中、正大对应描述，即模糊集合为{NB，NM，NS，ZO，PS，PM，PB}。模糊控制的关键是建立模糊规则，主要考虑在保证响应的基础上能够稳定，避免振荡，处理好稳定与振荡的关系。建立模糊规则的基本原则是：遇到横向偏差较大情况，以减小偏差为主；遇到横向偏差较小情况，注意防止超调，保持系统稳定。建立模糊规则前对横向偏差Pe和航向偏差θe的正负作出约定：Pe在车辆前进方向偏向右侧则为正，偏向左侧则为负；当前航向与预定路径的θe逆时针则为正，顺时针则为负。车辆的不同位置如图8所示，其中虚线为预定路径。

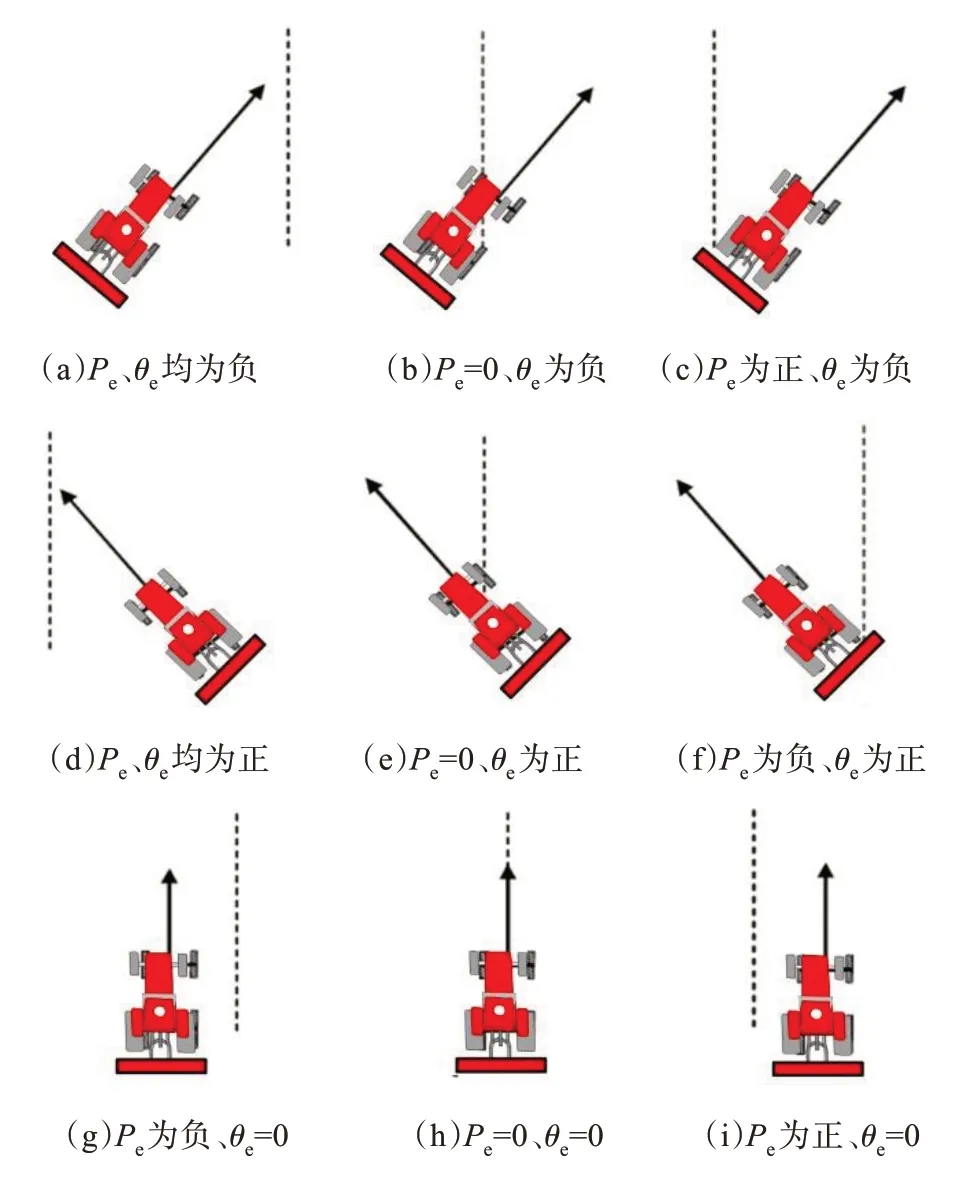
图8 车体与预定路径位置关系

建立的车辆模糊控制规则共有49 条，组合后见表1，表1 中Lq的取值由Pe、θe共同确定。模糊控制曲面如图9 所示，当遇到误差较大情况时，输出的前视距离较小，能够尽快减小误差，当遇到误差较小情况时，输出的前视距离较大，能够保持系统稳定。

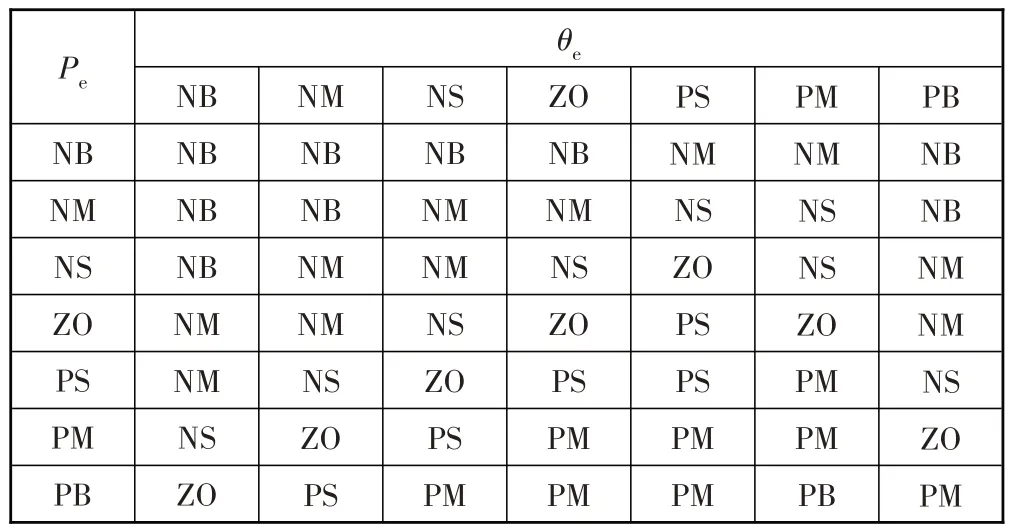
表1 模糊规则控制表

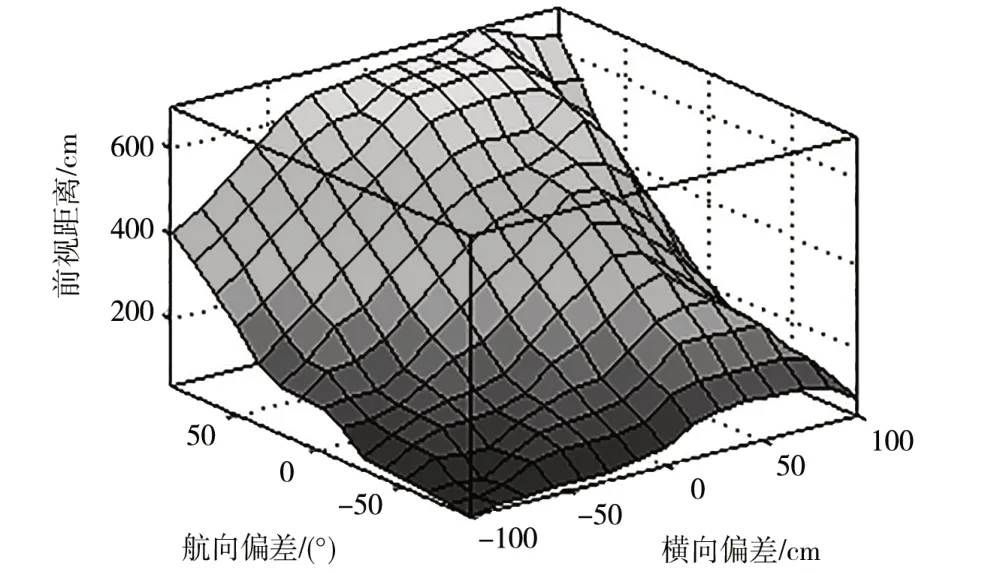
图9 模糊控制曲面

3.3 模糊推理与清晰化

模糊推理是根据模糊控制规则进行模糊语言解释的过程，将Pe、θe输入模糊控制器，得到合适的Lq模糊语言。清晰化是指将输出变量的模糊语言转化为清晰值，常用方法包括重心法、最大隶度法、系数加权平均法、中位数法等。考虑重心法可以包含Pe、θe的所有信息，所以本文采用重心法进行清晰化处理。

3.4 路径跟踪仿真

基于MATLAB/Simulink 搭建仿真模型，包括简化的运动学模型、纯追踪模型、模糊控制模型、转向控制模型。

将得到的Lq作为输入条件，得到模糊自适应纯追踪模型，如图10所示。

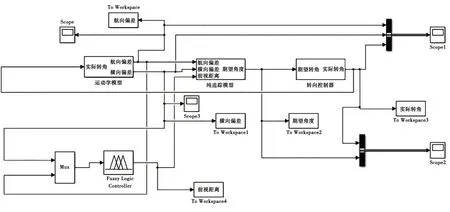
图10 模糊自适应纯追踪模型

3.5 仿真结果分析

针对图10 仿真模型设定初始条件，θe1=10 °、Pe1=15 cm、θe2=-10 °、Pe2=-15 cm、v=1 m/s、L=0.6 m，仿真结果如图11、12所示。

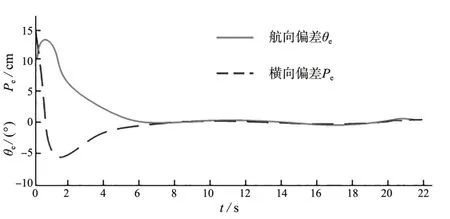
图11 仿真结果（θe=10 °，Pe=15 cm）

由图11 可知，当θe、Pe为正值且偏差较大时，模糊控制器发挥作用使偏差快速缩小。进行路径跟踪时，在0～1 s过程中，θe先增大后减小，Pe由正值减小为负值，从1 s 左右开始，θe、Pe二者的绝对值均不断减小直至趋于0，达到车辆路径跟踪目标。

由图12 可知，当θe、Pe为负值且偏差较大时，模糊控制器发挥作用使偏差快速缩小。进行路径跟踪时，在0～1 s过程中，θe先减小后增大至正值，Pe的绝对值先增大后减小，从1 s 左右开始，θe、Pe二者的绝对值均不断减小直至趋于0，达到车辆路径跟踪目标。

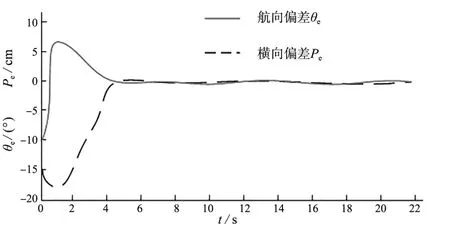
图12 仿真结果（θe=-10 °，Pe=15 cm）

设置仿真模型的初始条件：v=1 m/s、初始位置为（6，0）、θe=45 °、Pe=1 m，预定路径为直线X= 5 m，仿真结果如图13 所示，初始位置和预定路径的横向偏差为1 m，仿真结果中路径跟踪的最大横向偏差为0.055 m，误差为5.5%，根据经验判断，此误差可以接受，车辆最终沿着指定路径行走，验证了算法的可行性。

图13 路径跟踪仿真

4 结束语

本文对智能汽车的路径跟踪控制建立运动学模型，基于纯跟踪算法和模糊控制相结合方法，通过自适应调节前视距离实现路径跟踪。通过MATLAB/Simulink 搭建仿真模型，以不同的横向偏差、航向偏差作为初始条件进行仿真，结果表明所建立的仿真模型能够实现车辆路径跟踪，理论上验证了该算法的可行性。