谈基于课本的高中数学写作选题

仓万林　高强　李红

【摘 要】数学写作是一种学习方式，课本是学习中的基本材料，也是高中数学写作的素材来源之一．文章以高中数学人教A版第一册函数内容为例，按数学写作的常见类型：学习感悟、解题研究、数学建模与应用、数学文化与科普类型，对从课本中选题进行介绍，并给出部分学生数学写作实践案例．

【关键词】数学写作；课本；素材；函数

随着课程改革的不断深入，学科融合活动得到了越来越多的关注，其中高中数学写作是高中学生以数学为主题和材料的写作活动，而选题又是高中数学写作活动中重要的一个环节．

数学写作从课本中选题体现了选题方便性原则．课本是教学最重要的课程资源，是开展数学活动的极好素材.课本中的例题、习题等是编者从学科整体的角度出发，精心挑选，符合学生的认知特征．阅读是写作的基础，课本中很多有价值的阅读材料，比如数学文化，包括数学史、数学家介绍等，可以帮助师生更好地理解数学．课本习题具有典型性，是解题训练的模板，也是思维训练的典范．课本中的“探究拓展”类问题，未必适合所有的学生．平时教学中，由于条件的限制，教师往往不能恰当使用这些素材，而数学写作活动具有多元、灵活、开放、创新等特点，正好可以充分利用课本资源．

目前，高中数学人教A版教材使用范围最为广泛，笔者以人教A版第一册中的函数内容（第三章“函数的概念与性质”和第四章“指数函数与对数函数”）为例［1］，谈从课本中进行数学写作选题的问题．函数是贯穿高中数学的一条主线，函数概念及其数学思想方法已渗透到数学的各个领域，是进一步学习数学的重要基础．

“数学写作”学校联盟成立于2017年，目前已经有100多所学校加盟.根据联盟经验，兼顾数学写作活动的方便，数学写作按内容性质一般分为以下四类：学习感悟、解题研究、数学建模与应用、数学文化与科普.这些内容，都能在函数内容中找到相应的素材．

1 学习感悟类

案例1 （第73页第10题）一个老师用５分制对数学作业评分．一次作业中，第一小组同学按座位序号1，2，3，4，5，6的次序，得分依次是5，3，4，2，4，5．你会怎样表示这次作业的得分情况？用x，y分别表示序号和对应的得分，y是x的函数吗？如果是，那么它的定义域、值域和对应关系各是什么？

推荐理由：刚刚接触函数概念的学生，由于概念高度抽象与符号化，觉得函数概念难以理解，特别是用符号语言刻画函数．问题用叙述的形式展现了函数的定义，对学生认识函数的定义和本质有重要促进作用．学生写下学习感受，是对函数概念进一步“体悟”的过程，对函数概念的认识会更加清晰．在数学写作活动中，笔者特别关注能反映函数本质的课本题目，曾经咨询过部分一线教师，他们在教学中并没有选择或者重视这个问题．

数学写作方向建议：（1）分别用列表法、图象法、解析法表示这个函数；（2）体会问题中的转化过程，感受函数中“对应关系”本质．

部分学习感悟类素材推荐如表1.

学生写作：函数都有图象吗？（节选）

当我们想念某个好友时，常做的事情是什么呢？许多人的动作往往是动动手指，刷刷好友的朋友圈，或者逛逛他的QQ空间，看看他的生活照吧！

函数的图象就是函数的写真，函数的图象是刻画函数性质的重要工具之一．我们对函数的图象情有独钟是有原因的，它能直观形象地表示出函数的变化情况，就像我們看到了好友的照片一样亲切．另外，函数图象也可以帮助我们解决许多从传统解析式出发难以解决的问题，也就是同学们常用的“数形结合”的工具．那么，函数都有图象吗？

许多同学马上会提出问题：有的函数图象，我们用手工作图的方法的确不容易画出来．这种情况好解决，我们可以借用现代化技术手段，比如手机软件中许多画图APP的功能还是挺强大的．下面我们就用几何画板作出函数y=ln1－x/1+x图象，如图1.图1

我们知道要证明一个命题不成立时，除了直接证明之外，常用的一个策略是举反例.我们能找到一个作不出图象的函数吗？

狄利克雷函数就是一个很好的例子，狄利克雷函数可以简单地表示分段函数的形式D（x）=1，x为有理数，0，x为无理数.在中学范围内，我们可以理解的此函数的基本性质有：（1）定义域为整个实数集R；（2）值域为{0，1}；（3）函数为偶函数；（4）无法画出函数图象，但是它的函数图象客观存在；（5）以任意正有理数为其周期．

狄利克雷函数的出现，其重要意义不仅仅在于给我们造出了一个函数图象不存在的示例，而且极大地推动了函数概念的发展，使人们对函数的认识超越了解析式的限制．

让我们好好静下心来梳理一下，高中阶段还遇到哪些感觉怪怪的函数，可不要小看了他们呀，函数演变中一个重要因素就是这些“怪”函数的出现.还是刚才的狄利克雷函数，是周期函数，但不存在最小正周期，是不是又颠覆了我们对函数周期性的认识呢？

2 解题研究类

案例2 （第101页第12题）试讨论函数y=x－1/x的定义域、值域、单调性、奇偶性，并画出函数图象．推荐理由：作为对照，不妨看一下，课本中的另外几个值得关注的问题．

（第79页例3） 根据定义证明函数y=x+1/x在区间（１，＋∞）上单调递增．

（第92页） 探究函数y=x+1/x的图象与性质．

学生完成这些问题后，往往会产生一种思维定势，只要出现和或积为定值的条件，就可以用基本不等式求最值（值域）．教师往往关注的是函数性质和基本不等式的整合使用，而该问题结构小巧，能有效帮助学生学会辩证地看待基本不等式的应用．看似变化不大的课本题却可以提升学生的鉴赏和识别能力，在函数结构的细微变化中体会其性质的根本性变化．

数学写作方向建议：（1）问题看起来很像大家熟悉的“对勾函数”，对勾函数的性质你掌握了吗？（2）在和对勾函数的比较中，有哪些体会？（3）还可以使用哪些技术手段或者工具分析这个问题？部分解题研究类素材推荐如表2.

3 数学建模与应用类

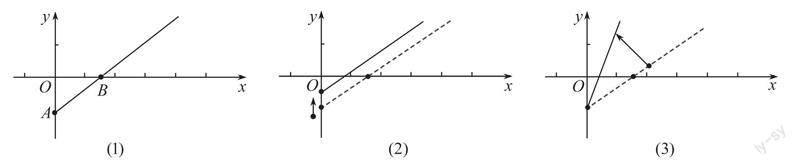
案例3 （第96页第4题）图（1）是某条公共汽车线路收支差额y关于乘客量x的图象．（1）试说明图（1）上点A，点B以及射线AB上的点的实际意义；

（2）由于目前本条线路亏损，公司有关人员提出了两种扭亏为赢的建议，如图（2）（3）所示．你能根据图象，说明这两种建议是什么吗？

推荐理由：该问题有浓厚的现实生活色彩，引导学生关注数学与实际生活的联系，也是数学课程思政教育的良好素材．对函数图象的解读，体现了“用数学眼光观察现实世界，用数学思维思考现实世界”，而数学写作活动则实现了“用数学语言表达现实世界”的能力．

数学写作方向建议：（1）调查所在城市的公共交通的运营情况，进行数据统计和分析，为新形势下公共交通的优化给出“高中学生”方案;（2）跟踪某条确定线路的公交车运营情况，用数学的模型刻画其经济指标，尝试给出优化方案．

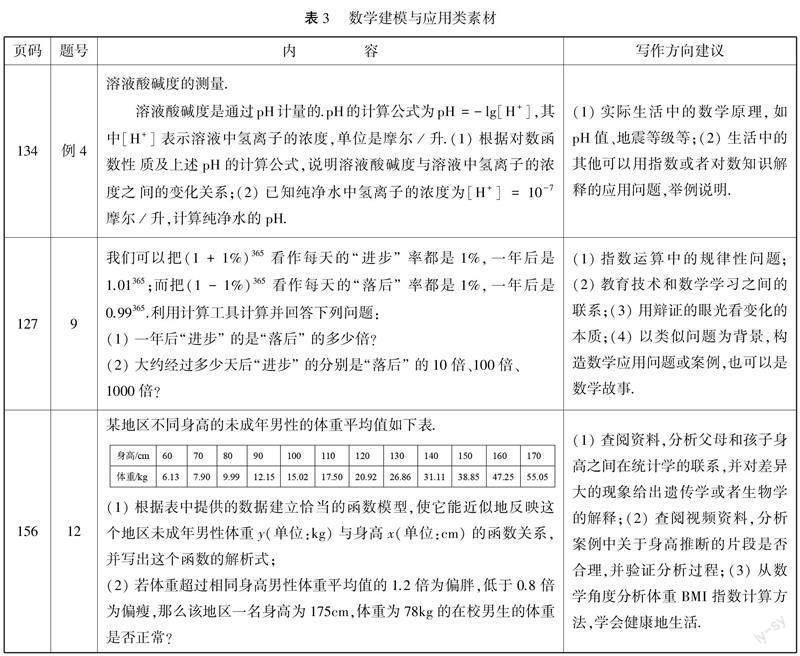
部分數学建模与应用类素材推荐如表3.

学生写作：西瓜中的数学（节选）

西瓜是最神奇的水果．炎炎夏日三件套：空调、西瓜、WiFi.没有看懂吗？恭喜你成了“吃瓜群众”．

吃西瓜也是有学问的，首先要过了买西瓜这一关.于是，我想到了数学家、院士王元买瓜的一段故事：王元先生家楼下有位卖西瓜的魏师傅，大瓜三元一个，小瓜一元一个．王元让太太买大的，王太太买了两个大瓜，又有些犹豫：“大的贵两倍呢……”王元笑着说：“大的比小的合算！”王太太点头又摇摇头：“恐怕还是大的吃亏．”结合故事，试分析买西瓜中的数学道理．

公说公有理，婆说婆有理．清官难断家务事，其实还是可以断的，西瓜挑大选小也有学问，这里就有一个数学建模问题．

即便是价格一样、同样甜，就不用挑了？还是要挑的，挑什么呢？恐怕许多人没有思考过这个问题．买同一品种的西瓜时，西瓜的质量越大，买瓜的钱越多．当然大家都希望西瓜瓤占整个西瓜的比例越大越好．假设我们把西瓜都看成球形，半径为R，西瓜的密度看成是均匀的，西瓜皮的厚度都是d（这种假设在实际问题中叫做抽象，可以使问题的讨论具有可操作性），买大西瓜还是买小西瓜合算呢？西瓜瓤占整个西瓜的比例为：

看来还是王元先生厉害呀．

有同学马上会发现，刚才的问题中，我们假设西瓜的密度是均匀的，这其实和实际情况有所差异.一般来说，西瓜皮的密度要比西瓜瓤的密度大一些．你能尝试着分析一下吗？4 数学文化与科普类

案例4 （第75页）阅读与思考：函数概念的发展历程.

推荐理由：了解函数概念形成和发展的历史，对学生理解函数的本质有帮助，也体现了数学文化在数学理解中的潜移默化的教育功能．通过函数的历史，可以解释我们为什么会对函数的解析法特别偏爱．我们对函数的部分片面认识，在函数历史上大有市场，许多数学家当初也有这样的困惑．重温函数历史，我们学会“像数学家一样思考”．

数学写作方向建议：（1）查阅资料，了解函数发展的历程，认识函数概念的几种主流观点，介绍代表性数学家或者数学家的故事等;（2）不同函数观点中，哪一种是我们感觉使用最方便的？说明其理由．部分数学文化与科普类素材推荐如表4.

在数学写作活动中，选题要注意充分挖掘课本中的素材．如何更好地使用课本，对优化学生的数学学习体验有重要作用，对教师而言，也是教学理念和智慧的体现．

参考文献

［1］人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心. 普通高中教科书·数学·必修一（第一册）（A版）章建跃，李增沪．普通高中教科书数学（第一册）［M］．北京：人民教育出版社，2019．

作者简介 仓万林（1975—），男，江苏盐城人，中学高级教师；“数学写作”学校联盟秘书长，《新世纪智能（新高考数学版）》执行主编；著有《数学文化行动研究的实践和思考》等，主编“数学写作”学校联盟学生作品集《数写世界》《浪花朵朵》.

高强（1981—），男，江苏江阴人，中学一级教师；江阴市数学基本功大赛一等奖，江阴市教学新秀.

李红（1981—），女，江苏江阴人，中学一级教师；全国新青年数学教师工作室理事；发表论文10余篇.

基金项目 江苏省教育科学“十四五”规划课题“指向深度学习的高中数学写作实践研究”（D/2021/02/64）；江苏省基础教育前瞻性教学改革试验项目“数学写作提升核心素养的实践研究”（2020JSQZ0147）.——以人教A版第一册函数内容为例