BES-RBF神经网络支持下的可见光定位系统

王玲燕,秦 岭,郭 瑛,徐艳红,赵德胜

(内蒙古科技大学信息工程学院,内蒙古 包头 014010)

随着物联网技术的发展,人们对于位置服务的需求也大大增加,GPS可满足人们对室外定位导航的需求[1-2],但室内复杂的环境容易对卫星信号产生遮挡,导致GPS在室内定位方面误差增大。不同建筑的室内布局存在较大差异,需要更高的精度分辨不同的特征[3]。目前常见的室内定位技术有无线局域网(WLAN)、射频识别(RFID)、蓝牙、ZigBee、地磁等,然而这些技术都存在一些不足[4-8]。可见光定位技术具有无电磁辐射、低成本、高定位精度、能耗较低优点,能弥补传统定位技术的不足,非常适用于室内定位[9-13]。

随着机器学习和深度学习算法的进一步发展,许多学者将新型学习算法与传统室内定位技术相结合,获得了较好的定位结果。文献[14]提出了一种基于隐马尔可夫模型的可见光与惯导融合定位算法,所提算法能在2500 m2室内停车场中预测用户的运动轨迹,平均定位误差约为3.35 m。文献[15]提出了一种基于改进混合Bat算法的可见光三维定位方法,在1.5 m×1.2 m× 2 m空间内平均定位误差为3.64 cm。文献[16]提出了一种基于改进免疫粒子群算法的VLC室内三维定位系统,并采用卡尔曼滤波算法减小了环境干扰对接收功率的影响,仿真试验平均误差为3.12 cm。文献[17]提出了一种基于四象限光电探测器和改进遗传算法的可见光定位系统,该方案在平均定位时间较短的情况下,可以获得较高的定位精度和稳健性。文献[18]提出了一种基于深度学习和数据驱动的高速车辆稳健VLP系统,基于BN-CNN模型的UID解码方式,支持的移动速度达38.5 km/h。由上述研究现状可知,传统的室内定位技术与新型学习算法相结合可以获得更好的结果,然而目前关于可见光定位的研究大都仅考虑可见光直射链路,导致仿真建立的定位系统在实际应用时会出现较大的误差[19]。

为了更好地应用于实际环境并进一步提高定位精度,本文综合考虑直射链路和两侧不规则墙壁的反射建立定位模型,并提出一种秃鹰搜索算法优化径向基神经网络(BES-RBF)的单LED灯的定位算法,结合WKNN,得到高精度定位模型。在定位系统中,4个PD(Power Delivery)接收到的功率及位置构成指纹库数据;通过秃鹰搜索算法优化RBF网络初始权值和阈值;数据输入优化后的RBF网络,得到初步定位信息;结合WKNN对部分误差较大的点进行修正,以期得到精确的位置信息。

1 基本原理

1.1 可见光信道模型

将定位空间大小设置为3 m×3 m×3 m,考虑空间两侧墙壁的不规则反射链路,定位模型如图1所示。LED作为信号发射源位于顶部中央,两侧阴影部分为反射面,接收器由一个水平PD和3个倾斜PD组成(具体结构如图2所示),放置在距离地面一定高度的位置上。

图1 定位模型

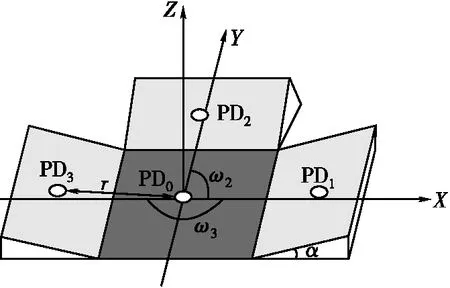
图2 接收器模型

待测点为水平PD的中心,表示为(Xr,Yr,Zr),倾斜PDj与水平PD的关系可以表示为

(1)

式中,α为PDj(j=1,2,3)的倾斜角;ωj为PDj的方位角;r为倾斜PDj中心到水平PD中心的距离。

可见光传输链路如图3所示。假定光源LED服从朗伯模型,直射链路信道增益HLOSj可以表示为

图3 可见光传输链路

(2)

式中,A为接收机PD的有效接收面积;dj为接收PDj到LED光源之间的距离;θj为接收PDj的入射角;φ为光源发射角;Ts(θj)为光学滤波器增益;g(θj)为聚光器增益;ψc为接收器的视场角;m为光源的朗伯阶数。g(θj)和m的公式[20]如下

(3)

式中,φ1/2为光源的半功率角,即在此角度上的LED光源辐射功率是中心功率的1/2;n为接收器透镜折射率。在考虑不规则墙壁的反射链路中,信道增益HNLOSωj的公式[21-22]如下

(4)

式中,diω为LED到反射面元sω的距离;dωj为反射面元sω到接收器PDj的距离;(xω,yω)为反射面元sω的二维坐标;hiω为LED到反射面元sω的垂直距离;hωj为反射面元sω到接收器PDj的垂直距离;ρ为反射系数;ΔAω为反射面元sω的面积;LED灯的坐标为(xi,yi,zi);ni=[sinβicosαisinβisinαi-cosβi],为对应法向量;反射面元sω坐标为(xω,yω,zω),法向量为nω=[sinβωcosαωsinβωsinαωcosβω];nj=[sinβjcosαjsinβjsinαjcosβj],为第j个PD的法向量;法向量中的α和β分别表示各向量与x轴和z轴的夹角。

整个通信环境的信道增益最终可以表示为

(5)

在可见光信号传输链路中,接收PDj的接收功率Prj与LED的发射功率Pt的关系可表示为

Prj=PtHj

(6)

1.2 RBF神经网络

RBF神经网络是一种前馈式网络,其思想是用径向基函数作为隐层各单元的基(本文采用的基函数为高斯函数),将输入向量从低维度变换至高纬度,使得在低维度上的线性不可分问题在高维度上线性可分[23-24]。该方法有两个阶段:①用自组织聚类方法为基函数确定合适的数据中心,并根据中心间的距离确定隐节点的扩展常数,求解隐含层的基函数的中心和方差;②用有监督学习算法(一般采用梯度法)训练输出层权值。结构如图4所示,实现过程如下。

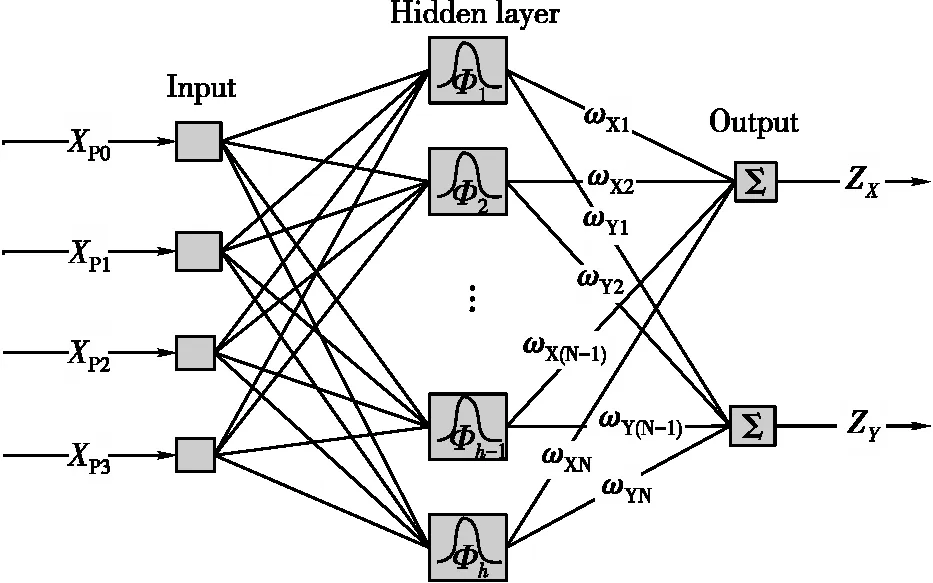
图4 RBF神经网络结构

(1)采用K-means聚类方法求得基函数中心c。

a. 初始化:随机选取训练样本作为初始聚类中心ci(i=1,2,…,h),ci={Pr0,Pr1,Pr2,Pr3},h为隐含层节点数,Prj(j=0,1,2,3),表示各PD接收功率。

b. 计算中心ci与输入的训练样本xg={Pg0,Pg1,Pg2,Pg3}之间的欧式距离,将xg按最近邻规则分配到各个聚类集合ϑi(i=1,2,…,h)中。

c. 聚类中心重整:计算ϑi中训练样本的平均值,求得新的聚类中心ci,直至新的聚类中心不再发生变化,此时的ci即为RBF神经网络最终的基函数中心,否则返回步骤b,进行下一轮求解。

(2)计算方差σi。高斯函数的方差σi计算公式为

(7)

式中,cmax表示所选中心间的最大距离。

(3)计算隐含层和输出层之间的权值。

通过最小二乘法可以计算得到权值,公式为

(8)

式中,xg=[Pg0Pg1Pg2Pg3]为第g个输入样本;ci为第i个隐含层节点在步骤(1)最终得到的基函数中心;G为输入样本总数。

网络最终的输出可以表示为

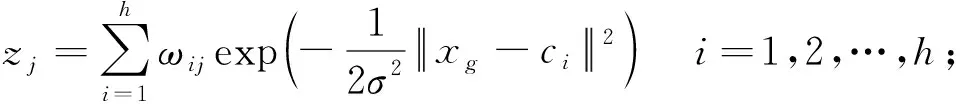
(9)

式中,J为输出节点数,本文输出为二维坐标,J取2。

1.3 秃鹰搜索算法

秃鹰搜索算法(BES)是一种元启发式优化算法[25],模拟了秃鹰寻找猎物时的狩猎策略及智能社交行为,具有较强的全局搜索能力。该算法分3步完成:首先,秃鹰根据猎物的浓度选择一个特定的搜索区域(一般选择浓度大的区域);然后,秃鹰在搜索区域内进行螺旋搜索;最后,秃鹰不断改变飞行高度,直至成功获取猎物。

(1)选择空间,该阶段选择猎物最多的空间为搜索空间,即

Wnew,i=Wbest+αr(Wmean-Wi)

(10)

式中,α∈[1.5,2]为控制位置变化的参数;r为0～1之间的随机数;Wbest为根据之前搜索空间确定的最佳位置选择的搜索空间;Wmean为之前搜索点的信息,该过程随机更改搜索点。

(2)搜索空间,秃鹰在搜索空间内螺旋飞行加速搜索,抓捕的最佳位置可表示为

Wi,new=Wi+y1(i)·(Wi-Wi+1)+x1(i)·(Wi-Wmean)

(11)

(12)

xr1(i)=r1i·sin(θ1i),yr1(i)=r1i·cos(θ1i)

(13)

θ1i=b·πrand,r1i=θ1i+Rrand

(14)

式中,b和R为控制螺旋轨迹的参数,b∈[5,10],用于确定中心点之间的角,R∈[0.5,2],用于确定搜索周期的数量。

(3)俯冲抓捕,从搜索空间的最佳位置俯冲至目标猎物,即

Wi,new=rand·Wbest+x2(i)·(Wi-c1Wmean)+

y2(i)·(Wi-c2·Wbest)

(15)

(16)

xr2(i)=r2i·sinh(θ2i),yr2(i)=r2i·cosh(θ2i)

(17)

θ2i=bπrand,r2i=θ2i

(18)

式中,c1,c2∈[1,2],增加了秃鹰朝向最佳和中心点的运动强度,因此最优解必须乘以一个随机数。

1.4 定位过程

1.4.1 BES-RBF算法

本文提出的定位系统首先利用秃鹰搜索算法对网络的权重和阈值进行评估,使其找到最优的向量个体,然后将其赋给RBF神经网络。流程如图5所示。BES-RBF算法实现步骤如下。

(1)输入样本数据。

(2)将RBF神经网络生成的权值和阈值作为BES算法的初始信息点。

(3)选择猎物最多的空间作为搜索空间。

(4)在搜索空间内螺旋加速搜索,获得最佳俯冲位置。

(5)从最佳俯冲位置抓捕猎物,得到最优的向量个体。

(6)将优化得到的权值和阈值赋给RBF网络。

1.4.2 误差修正

加权K近邻算法首先需要计算当前待测点的数据与数据库中的各个指纹数据之间的距离,并对距离进行升序排序,然后找到离待测点最近的K个参考点,为K个参考点的坐标分配权重,最后对K个参考点坐标的加权和求平均,得到待测点的位置。

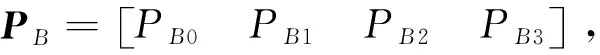
(19)

将DI按升序排列,并按权重为1/(DI+ε)的加权规则为前K个参考点的坐标分配权重,ε为一个常量,待测点的最终坐标为

(20)

2 仿真结果分析

本文的定位空间设置为3 m×3 m×3 m,LED灯的发射功率为10 W,用15 cm×15 cm的间隔对接收面进行划分,共441组数据构成训练集,以28 cm×28 cm的间隔对接收面进行划分,共121组数据构成测试集。具体参数见表1。

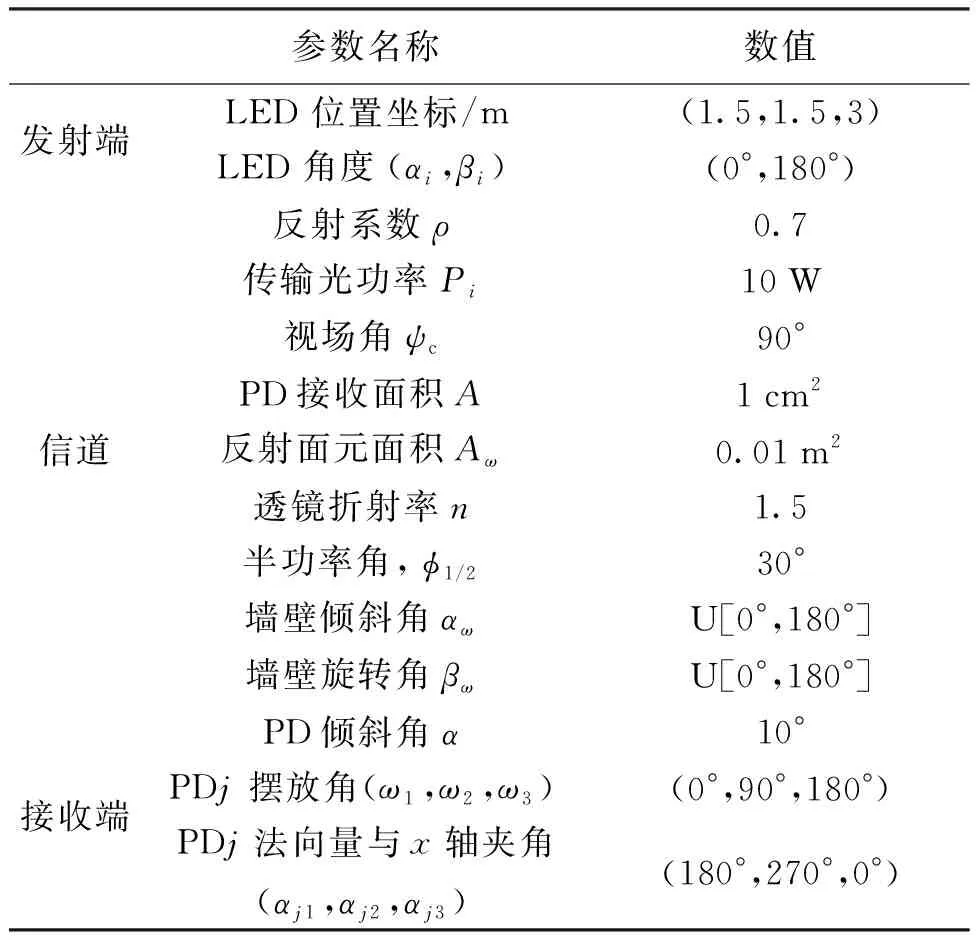
表1 仿真参数[19]

为了比较BES结合WKNN对RBF神经网络的优化效果,对比RBF、BES-RBF、RBF-WKNN及BES-RBF-WKNN这4种模型的定位效果,其RMSE见表2。可以看出,BES对RBF有部分优化作用,但整体优化幅度不大;WKNN优化RBF后的平均定位误差反而增大,同时结合BES和WKNN优化RBF后,平均误差下降了2 cm,优化效果明显。

表2 优化前后平均误差对比

为了更好地比较这4种模型的定位效果,绘制其误差累积频率分布曲线,如图6所示。由图6可知,RBF模型有80%的定位误差在10 cm内,BES-RBF模型有91%的定位误差在10 cm内,RBF-WKNN模型有85%的定位误差在10 cm内,BES-RBF-WKNN模型有93%的定位误差在10 cm内,BES-RBF-WKNN模型的整体定位性能更好。

使用WKNN优化定位结果时,K值对定位结果具有较大影响,为了对比不同K值的影响作用,将K取值1～7,绘制RBF-WKNN和BES-RBF-WKNN模型不同K值的平均误差曲线,如图7所示。

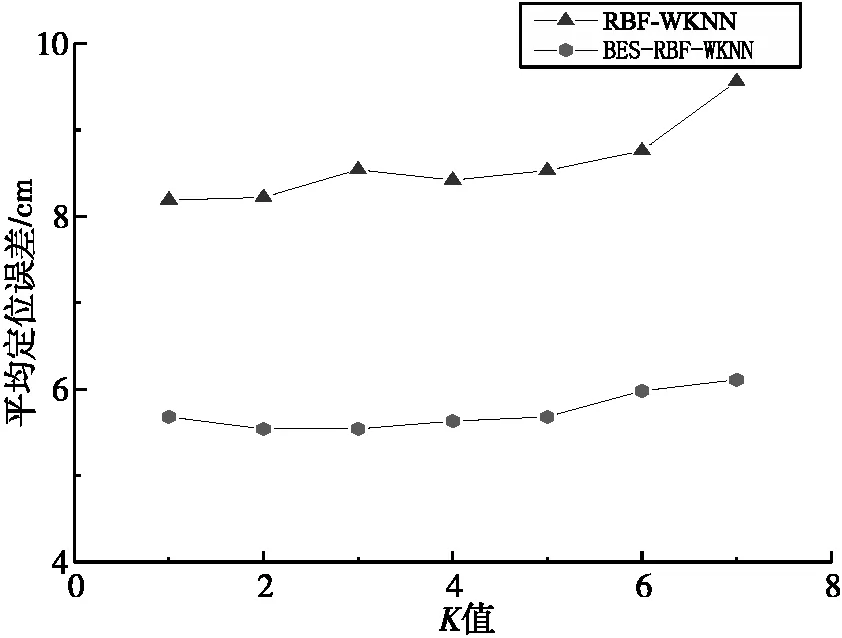
图7 不同K值平均定位误差对比

由图7可以看出,WKNN优化RBF时,随着K的增加,平均定位误差增大,K取1时平均定位误差最小,最小的平均定位误差仍比未优化时大,这是由于在选取拖累点时,将误差大于平均误差且接近平均误差的点包含在内,在进行加权K近邻计算时这部分点的误差增大。WKNN优化BES-RBF时,K在整个取值范围内的平均定位误差均小于未优化时的定位误差,整体优化效果明显,K取2时,平均定位误差最小,为5.54 cm。

为了更直观地对比4种模型的定位效果,绘制真实值和预测值的坐标对比图,如图8所示。

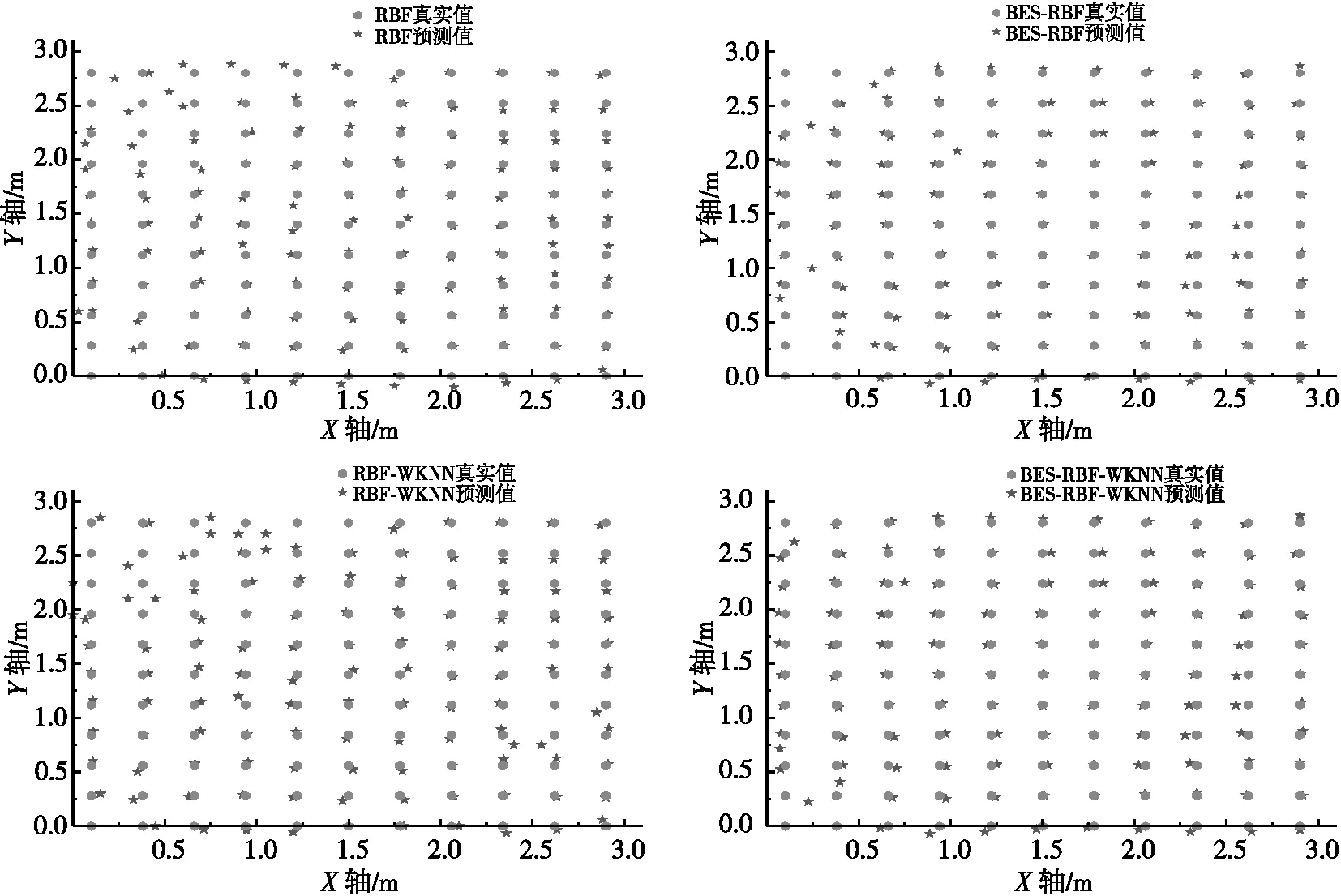
图8 4种模型坐标对比

由图8可知,BES对RBF的优化效果集中体现在待测区域的中心部分,优化后中心区域的待测位置与预测坐标基本重合,但边缘位置的误差相对较大。单独使用WKNN对RBF进行优化效果不理想,预测坐标偏离待测点位置较远。同时使用BES和WKNN优化RBF,效果明显,中心区域基本重合,边缘部分预测坐标与真实位置间的距离减小,仅极个别点能看出明显误差,整体效果良好。

为了更直观地比较优化算法对神经网络的作用,绘制不同定位模型的误差直方图,如图9所示。第1列为误差在[0,0.05] m内的频数,第2列为误差在(0.05,0.1] m内的频数,第3列为误差在(0.1,0.2] m内的频数,第4列为误差在(0.2,0.4] m内的频数,第5列为误差在(0.4,0.8] m内的频数。可以明显看出,使用BES后,误差在5 cm内的频数增加,误差较大的点数明显减少。使用WKNN后,对误差大的点的修正作用更加明显。

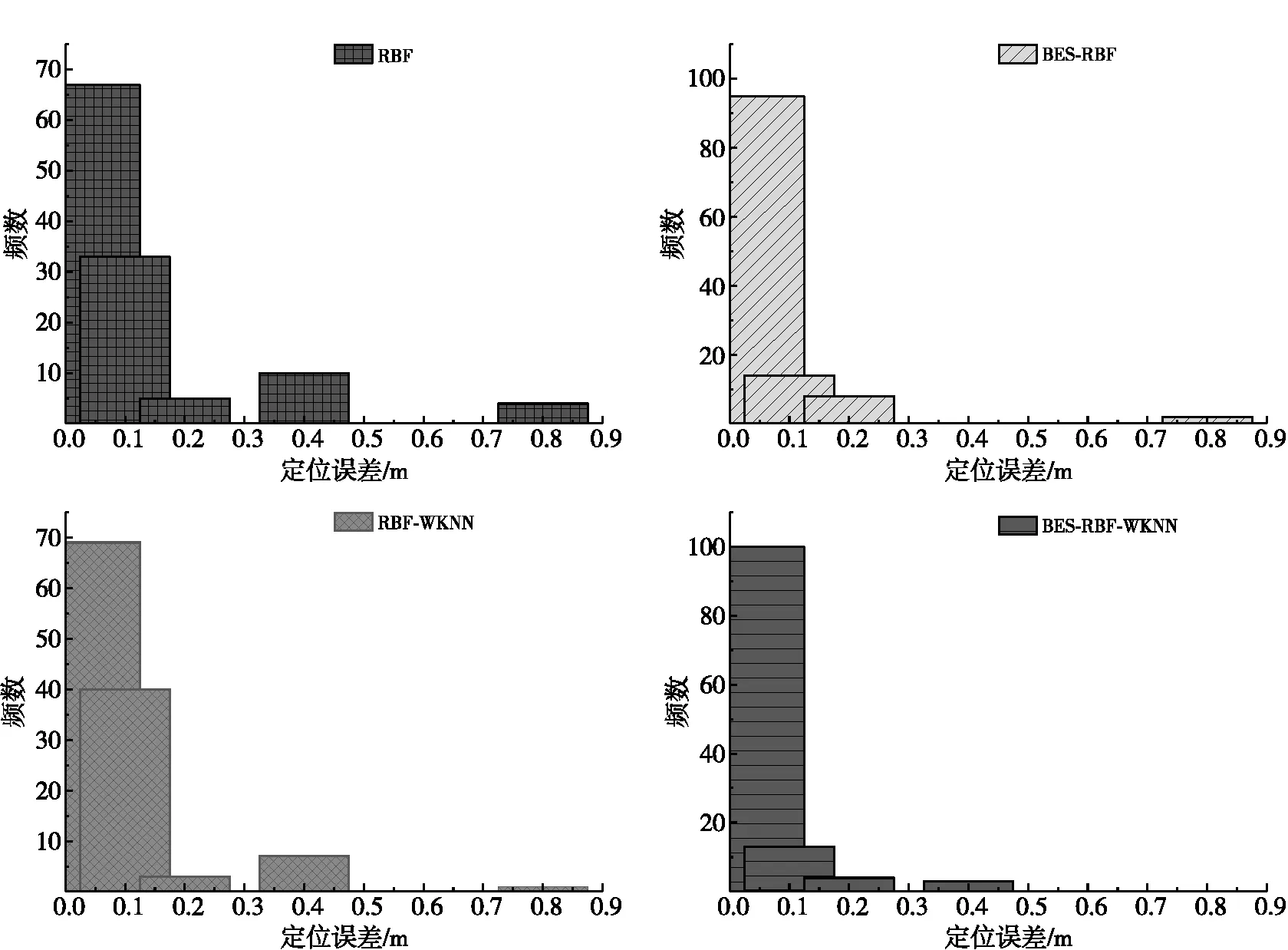
图9 误差直方对比

为了说明本文算法的优越性,将优化模型与其他模型进行对比,结果见表3。

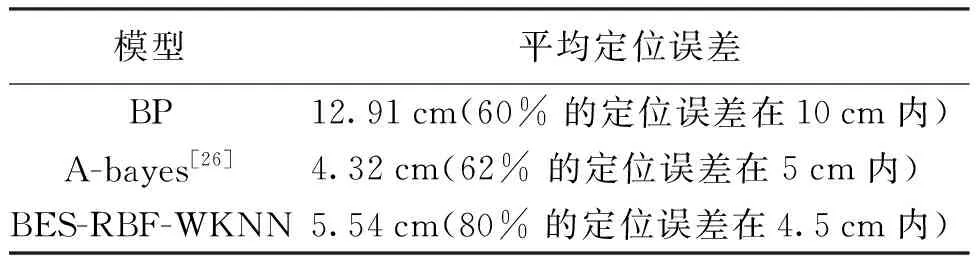
表3 不同模型性能对比

BP网络的定位误差较大,A-bayes的平均定位误差虽然小于BES-RBF-WKNN,但5 cm内误差占比小于本文算法。对比发现,本文算法优于其他算法,可以实现室内精确定位,能满足大多场景的定位需求。

3 结 语

本文提出了一种秃鹰搜索算法优化径向基神经网络(BES-RBF)的单LED灯的定位算法。该定位模型考虑了直射链路和不规则墙壁的反射链路,根据PD接收到的光功率值构建指纹库,将指纹数据输入BES优化后的RBF网络,实现初步定位,再结合WKNN对误差较大的点进行修正,实现室内高精度定位。本文在3 m×3 m×3 m的定位空间进行仿真试验,优化后的平均定位误差为5.54 cm,80%的定位误差在4.5 cm内。将本文算法与其他算法进行对比发现,本文算法的定位精度更高,稳定性更好,且使用单灯定位避免了其他光源的干扰,可适用于小型室内定位场景实现高精度定位。