二维激光雷达的实时三维重建方法
陈恬宇,孙立双,车德福
(1. 沈阳建筑大学,辽宁 沈阳 110168; 2. 东北大学,辽宁 沈阳 110819)
中国是斗轮堆取料机制造与应用大国,但目前各大煤炭港口、料场堆取料作业均为人工控制,普遍存在智能化程度偏低的问题,实现智慧料场无人化堆取料的关键是对料场料堆三维模型的实时显示。获取真实物体的三维模型,称为三维重建[1]。通过图片信息进行二维或三维重建是传统的三维重建技术[2]。激光雷达测距技术的发展为三维空间数据的获取提供了一种全新的技术方法,它可用于精准快速获取物体二维或三维数据,同时实现目标物体或场景的三维重建[3]。
三维激光扫描仪是激光扫描建模技术的主要仪器,尽管通过三维激光扫描仪能够精准快速地获取三维点云信息,但由于三维激光扫描仪价格昂贵,并不能广泛适用于实际应用,且对于精度要求不高的场景,性能过剩[4]。
在二维激光雷达的三维点云获取的研究中,文献[5—7]通过伺服电机驱动二维扫描仪的俯仰旋转完成了三维扫描,已被广泛应用于自动化机器人探测定位防撞系统和复杂地形检测。国内外针对二维激光扫描仪的三维重建试验及算法研究主要集中于获取区域内三维点云数据[8-14],实现三维扫描功能,但在二维激光雷达的三维点云配准尚未有研究应用。
在点云的三维重建研究中,文献[15]提出最近点迭代(iterative closest point,ICP)数据配准方法,即将当前数据与前一帧数据通过最近点迭代匹配,得到相对位置变化量。文献[16]分别针对分散性、数据量大、随机性、复杂度高提出了ICP算法实际使用问题。文献[17]提出了基于单位四元数的ICP改进算法,引入四元数求解变换矩阵,提高配准时间与精度。文献[18]提出了引入四元数作为空间旋转变换的描述算子,实现了相邻两站点的高精度三维点云配准。
本文源于某单位基于多源时空数据获取的臂式斗轮堆取料机无人值守智能平台研发及应用项目,提出在二维激光雷达中基于空间坐标变换算法的三维点云数据算法,以期实现二维激光扫描仪的三维料堆扫描。同时,针对两台相对位置不变的二维激光扫描仪,提出在点云配准中基于四元数法的多组旋转平移矩阵求均值解算法,对初步配准后的三维点云数据,基于四元数算法进一步优化配准,最后添加多个控制点,以此获取并验证点云配准精度。
1 基于空间坐标变换算法的三维点云数据生成算法
1.1 构建三维点云获取流程
试验器材采用两台SICK LMS511-10100 PRO二维激光雷达、两台飞越FY-SPT02中载云台,模拟斗轮堆取料机模型,搭建点云采集设备平台实物。如图1所示。

图1 点云采集试验平台实物
由两台二维激光雷达获取二维平面数据,与云台俯仰数据构成料机静态行走下的三维点云数据;由料机大臂俯仰数据、料机水平回转数据、基站和移动站差分定位的料机位置数据构成料机动态行走下的三维点云数据,如图2所示。通过旋转矩阵与欧拉角的空间坐标公式[19]变换获得局部点云数据,即单侧二维激光雷达下的三维点云数据,其流程如图3所示。
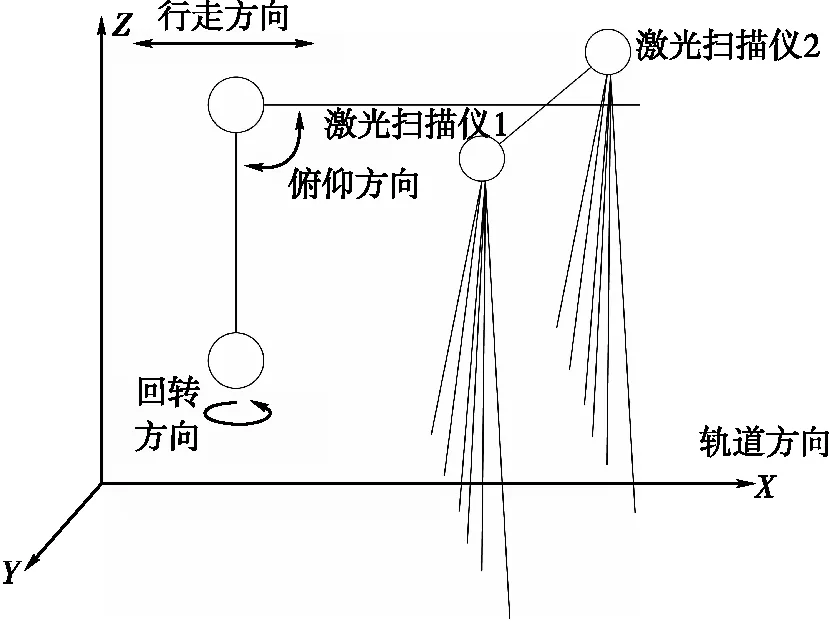
图2 三维点云获取模型(侧视图)
1.2 基于空间坐标变换算法的三维点云数据生成算法步骤
以二维激光雷达中心、云台中心分别构建两三维坐标系。二维点云数据通过云台的俯仰数据转换为三维点云,由空间变换公式求得局部点云数据,即二维激光雷达坐标系下三维点云数据。
(1)二维激光雷达为原点构建坐标系,扫描面获取二维点云数据(x,y)。
(2)以每帧扫描面二维点云数据构建n×4矩阵A,设点云坐标为(x1,y1),(x2,y2),…,(xn,yn),z轴为0。
(1)
(3)以云台为旋转中心为y轴,右手系绕y轴旋转坐标变换得4×4变换矩阵B。
(2)
(4)以云台中心点为原点建立云台坐标系(Xc,Yc,Zc),以二维激光雷达中心为原点建立雷达坐标系(Xw,Yw,Zw),设云台中心点与二维激光雷达中心点相对位置关系为Δx、Δy、Δz,欧拉角(roll、pitch、yaw),以此构建4×4转换矩阵C。
雷达坐标系转换到云台坐标系的过程分别由x、y、z轴旋转,得出相对欧拉角,即从雷达坐标系到云台坐标系的3个维度的旋转矩阵为
(3)
(4)
(5)
因此,由雷达坐标系到云台坐标系间的旋转矩阵Mc为
Mc=RxRyRz
(6)
构建云台坐标系(Xc,Yc,Zc)至雷达坐标系(Xw,Yw,Zw)转换矩阵为
(7)
由矩阵Mc求得云台坐标系至雷达坐标系转换矩阵C为
(8)
(5)构建云台坐标系下坐标变换矩阵D,即二维激光雷达坐标系下三维点云数据,为
D=ABC
(9)
1.3 基于空间坐标变换算法的三维数据生成算法试验结果
为了规范点云配准精度,精准测量点云误差,三维重建对象选用3个规则物体,测定试验对象尺寸:1号长方体(18.89 cm×12.43 cm×4.38 cm),2号长方体(12.21 cm×7.72 cm×2.26 cm),3号四棱柱(取侧面梯形面上底×下底×高为20.23 cm×24.63 cm×10.40 cm)。由空间坐标变换得到两侧三维点云数据,点云模型与实物模型一一对应。如图4所示。

图4 点云采集对象及其点云数据
2 基于四元数法的点云配准旋转平移矩阵优化算法
点云配准算法是在一个旋转平移矩阵初值已知的情形下(初值大概正确),进行运算得出比较准确的旋转平移矩阵[20-22]。
由于两台二维激光雷达的相对位置不变,通过点云配准算法,多次迭代计算,得到两组二维激光雷达下的三维点云数据的多组旋转平移矩阵。对多组旋转平移矩阵组求均值即可得到相对精度最高的旋转平移矩阵P。不仅保证了点云配准精度,还简化了点云配准迭代算法步骤,提高了配准速率。
2.1 多种旋转平移矩阵均值算法对比
对点云配准所得多组旋转平移矩阵求均值主要包括以下几种算法。
(1)利用欧拉角表示旋转,由欧拉角的3个参数相加后平均。
(2)由四元数表示旋转,通过四元数运算[23]求得旋转平移矩阵。其转换原理即是三维空间x、y和z轴的旋转,可由一个四维向量[θxyz]表示[24]。
(3)将旋转矩阵映射至单位元的切空间求平均,再映射回旋转矩阵。推导公式为
(10)
其中,xi为多组旋转矩阵;exp为矩阵指数;ln为矩阵对数。
(4)利用平均的定义数值求解,在数学规定中,给定元素集{x0,x1,…,xn},存在空间中一点x,使该点至元素集中n个元素距离之和最小。因此推导公式为
(11)
式中,SO(3)为旋转矩阵的特殊正交群,两个SO(3)元素之间距离定义为
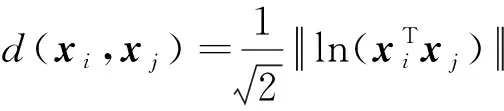
(12)
通过以上算法求解得到旋转矩阵均值,对平移矩阵直接由平均定义相加取均值即可。
为了验证以上4种算法的精确度,对单位三维旋转矩阵绕某一定点旋转,在给定范围内随机取样,样本数量为10组,3种线色矢量分别代表x、y、z轴的旋转,如图5所示。
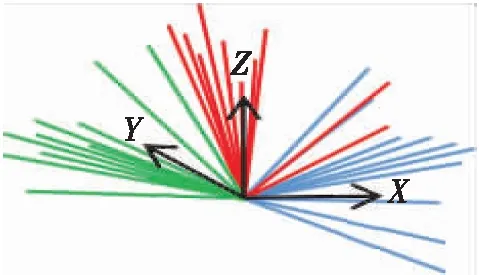
图5 三维旋转矩阵随机取样矢量分布


图6 旋转平移矩阵均值算法对比试验
2.2 点云配准旋转平移矩阵优化试验步骤
场景左侧、右侧分别为二维雷达激光雷达A、B,两者相对位置不变,获取左右两侧三维点云数据后,对其点云配准求得旋转平移矩阵多次取样。分别取多次点云A′与点云B′,求得旋转平移矩阵,多次迭代后,求得精度最高的旋转平移矩阵P。
(1)分别由激光雷达A与B获取多组点云数据。
(2)对多组点云数据α分别配准,由点云B′配准至点云A′,得多组旋转矩阵。
(3)基于四元数算法求相对精度最高旋转平移矩阵P。
(4)由多帧点云数据应用旋转平移矩阵P重新配准,得配准优化后多组点云数据β。
(5)对照试验结果。
2.3 点云配准旋转平移矩阵优化算法步骤
(1)四元数公式为
q=q0+q1i+q2j+q3k=[sv]
(13)
式中,q1、q2、q3均为实数,s=q0;v=[q1q2q3];i2=j2=k2=-1。i,j,k是一种旋转状态,-i,-j,-k分别代表i,j,k的反向旋转。
(2)由Rodrigues公式通过四元数求旋转矩阵式Rf。
(3)已知点云配准后旋转平移矩阵组Rn,转换为四元数组Fn。
当q0≠0,1+r11+r22+r33>0时
(14)
(15)
(16)
(17)
当q0趋近于0,1+r11+r22+r33趋近于-1时,rmax=r11、rmax=r22、rmax=r333种情况由四元数算法求解。
(4)由四元数加法公式求得四元数组Fn之和,公式为
Fn=s1+s2+v1+v2+…
(18)
(5)求四元数组均值并转换为旋转平移矩阵即相对精度最高旋转平移矩阵,并进行后续试验。
2.4 试验结果和分析
2.4.1 点云配准算法用时对比
点云配准通常采用的方法是最近点迭代(ICP)算法,但最近点迭代算法迭代次数过多且与运行时间过长。目前国内外引入基于KD-tree搜索法的ICP算法,显著提高运行时间降低迭代次数。为验证本文算法有效性,通过最近点迭代算法,基于KD-tree搜索法ICP算法,对同一三维点云集进行点云配准试验[25-26],其收敛速度对比见表1。可以看出,基于四元数法的配准优化算法节省了旋转平移矩阵迭代所耗时长,为点云的配准节省了大量时间。

表1 3种算法收敛速度对比
2.4.2 点云配准算法图像对比
在点云配准图像中,通过与传统ICP配准影像对比,图7(a)传统配准算法中3个规则物体发生位置偏移,这是由于图像特征匹配较差造成的,算法修正后,图7(b)局部纹理更加清晰,物体姿态正确,点云配准正确率大幅度提高。

图7 点云配准算法图像对比
2.4.3 点云配准算法精度测量
选取3个规则物体为试验对象,将三维点云数据导入Matlab,由pcread函数读取点云数据。选取对应点坐标,由欧式距离公式计算点云对应点距离与实际测量距离对比,从而获取点云精度,见表2。本文算法中点云精度为2 cm,满足本文课题要求。在给定相同条件下,基于四元数法的点云配准旋转平移矩阵优化算法具有良好的点云精度。
2.4.4 点云配准优化算法应用
采用臂式斗轮堆取料机模型模拟料机运转,二维激光雷达实测小型料堆,并通过全站仪测定标定点坐标与二维激光雷达点云测定标定点坐标对比试验,获取本文算法点云配准精度,如图8所示。
全站仪是目前应用最广泛的测量设备,单点测量精度高于SICK LMS511-10100 PRO,能够快速准确测得全局坐标系。本文采用圆形反射片中心孔作为标定点,对反射片中心点坐标通过全站仪与二维激光雷达分别测量,如图9所示。

图9 全站仪与激光雷达工作原理示意图
(1)选取4个不同直线,不同平面分布的标定点分别放置圆形反射片。
(2)使用全站仪进行坐标测量,以自身的坐标系构建全局坐标系;使用二维激光雷达扫描得到点云数据,进行坐标测量时使用自身局部坐标系,分别测得坐标数据。
(3)将全站仪测得坐标数据与点云测得坐标数据导入同一坐标系中,计算反射片之间相互夹角关系与距离关系;根据在空间中的位置关系确定扫描仪的反射片坐标与全站仪的反射片坐标之间的对应关系,获得两个坐标系之间的转换矩阵,从而将全部扫描数据转换至全局坐标系,求得两坐标差,见表3。

表3 各标靶全站仪坐标与点云坐标误差统计 m
由以上试验可得,本文算法下二维激光雷达测得点云配准数据与全站仪数据误差控制在2 cm以内。目前市面常用三维激光扫描仪(如Velodyne HDL-32E等)20 m内测距检测精度均在为±2 cm,完全满足试验项目要求。
3 结 语
本文采用C#语言,结合Visual Studio 2019,Matlab等开发工具进行系统开发,建立了基于二维激光雷达的三维点云重建系统,实现了以下主要功能:
(1)通过基于空间坐标变换算法的三维点云数据生成算法实现了由二维激光扫描仪对三维点云的实时获取。在满足规定项目使用要求下,极大降低了生产成本。
(2)通过基于四元数法的点云配准旋转平移矩阵算法,将二维激光扫描仪的三维点云精度控制在2 cm内,且当前帧配准速度达0.36 s,算法满足当前项目工程上对于三维点云的获取及三维点云重建精度与速率的要求,在实际工程应用中具有广泛的前景。
在实际研究过程中,本文采用两台相对位置相同的二维激光雷达,进行水平安装,因而不存在倾斜误差。但在实际应用中,由于激光雷达采集目的不同导致两台激光雷达相对位置发生更替时,该算法可能不再适用。

