不同循环加载路径下黄麻织物/聚乙烯复合材料的变形特性

汪泽幸, 周衡书, 杨 敏, 谭冬宜

(湖南工程学院 纺织服装学院, 湖南 湘潭 411104)

以麻纤维为代表的天然纤维增强热塑性复合材料,具有密度小、耐冲击性能好、吸音与隔热性能好、可回收利用、价格低廉等诸多优点,在交通运输和建筑等领域具有广阔的应用前景[1]。

为获得性能优良的麻纤维增强热塑性复合材料,并为其工程应用提供参考依据,目前,麻纤维及其与异种纤维混杂增强热塑性复合材料的制备及其力学性能已有较为全面的研究[2-6],但在工程设计和应用时,该类纤维增强热塑性复合材料使用依然受限,部分原因是其长期使用性能不稳定,同时,其循环荷载下的力学性能及破坏机制等也缺乏深入且全面的研究。

目前,众多学者围绕增强纤维的种类与含量[7-9]、纤维表面处理工艺[7,10]、异种纤维混杂[11]、增强结构形式[7,12-13]、基体种类[7,14]、环境条件[9,15]等因素对麻纤维增强热塑性复合材料的疲劳强度与寿命、疲劳后残余强度及疲劳破坏机制等进行了较为深入的研究,并探讨了其在不同加载路径下的力学行为特性。Haggui等[13]研究发现,分别循环加载时,相对于正交叠层结构,亚麻纱线单向叠层结构增强热塑性复合材料的能量耗散较高,但循环加载模量的衰减相对较低。基于逐级递增单次循环加载,Chilali等[15]探讨了亚麻斜纹织物增强热塑性复合材料的循环模量变化规律,Haggui等[13]亦对比分析了麻纤维热塑性复合材料滞回环的特点。逐级递增循环加载下,Aneta等[14]研究发现,亚麻纤维增强热塑性复合材料其各级疲劳应变与耗散能均随循环峰值应力的增加而增加,随循环次数的增加而快速增加并趋于稳定;同时,Gassan[16]就纤维表面处理对亚麻斜纹织物增强热塑性复合材料动态模量、能量耗散的影响规律进行了研究。此外,已有研究[17-19]亦基于分别循环加载和循环应力松弛加载,探讨了黄麻织物/聚乙烯复合材料的残余变形规律与能量耗散特性。

但对麻纤维增强热塑性复合材料力学性能研究,目前多采用分别循环加载和逐级递增循环加载路径,而对复杂加载路径下的力学行为特性,特别是变形特性方面的研究较少。基于此,本文基于热压法制备黄麻织物/聚乙烯复合材料,并对其在不同循环加载路径下的变形特性进行研究,分析其变形机制,以期为该类热塑性复合材料的工程应用与性能评估提供参考依据。

1 实验部分

1.1 实验材料

以商购黄麻机织平纹织物为增强织物,实测经、纬纱的线密度均为242 tex,经、纬向纱线排列密度分别为68、58根/(10 cm),面密度为323.6 g/m2。

采用YG747型通风式快速八篮烘箱将黄麻织物在90 ℃条件下烘2 h,去除黄麻织物中的水分。采用SY-6210-B-30型PLC程序控制压片机制备热塑性复合材料,单层黄麻织物双面铺设厚度为0.56 mm的聚乙烯膜,180 ℃条件下预热10 min,在180 ℃、1.0 MPa压力条件下热压5 min,保持自然冷却5 min,获得黄麻织物/聚乙烯复合材料。复合材料成品厚度为1.43 mm,黄麻织物的质量分数为23.38%,经换算后,可得黄麻织物的体积分数为19.33%。

1.2 试样制备与方法

机织物增强热塑性复合材料为经、纬向对称的正交异性材料[18-19],经、纬向试样的变形机制一致,力学行为特性相似,基于此,本文仅对经向试样进行测试和分析。沿经向制备矩形试样,试样宽度为(30±0.5)mm,长度为250 mm,有效夹持隔距为(150±0.5)mm。

为合理确定各级循环加载的峰值应力,以2 mm/min的加载速率对试样的拉伸断裂强度进行测试,实测5个有效试样的拉伸断裂强度,得到平均值为25.46 N/mm2。以此设定循环峰值应力σmax分别为4.66、9.32、13.98和18.65 N/mm2,分别为试样拉伸断裂强度的18.30、36.61、54.91和73.25%。

分别循环加载时,分别以速率υ一次性加载至对应的循环峰值应力σmax,后以同等速率卸载至最小应力σmin,并按此规律循环200次,即在同等循环峰值应力条件下循环加载200次。

多级循环加载时,以速率υ对试样进行逐级循环加载,各级循环次数N亦均设定为200次;按循环峰值应力σmax的变化路径,分为逐级递增和逐级递减循环加载2种路径。逐级递增循环加载路径下,循环峰值应力σmax施加序列为4.66、9.32、13.98、18.65 N/mm2,即循环峰值应力σmax按等差序列递增;逐级递减循环加载路径时,循环峰值应力σmax施加序列为18.65、13.98、9.32、4.66 N/mm2,即循环峰值应力σmax按等差序列递减。

为减少循环加载过程中因加、卸载速率过高而使实际循环峰值应力和最小应力产生的明显“过载”现象,加载与卸载速率υ均设定为2 mm/min。同时,为确保循环加载过程中试样始终处于张拉状态,循环应力最小值σmin均设定为0.23 N/mm2,约为材料拉伸断裂强度的0.92%。

实验均在环境温度为(22±3)℃、相对湿度为(65±5)%的条件下,在WDW-20C型微机控制电子万能实验机上进行。有效试样为3个,取代表性试样的实测曲线为研究和分析对象。

2 结果与分析

2.1 典型实验结果

3种循环加载路径下,代表性试样的应力-应变曲线如图1所示。

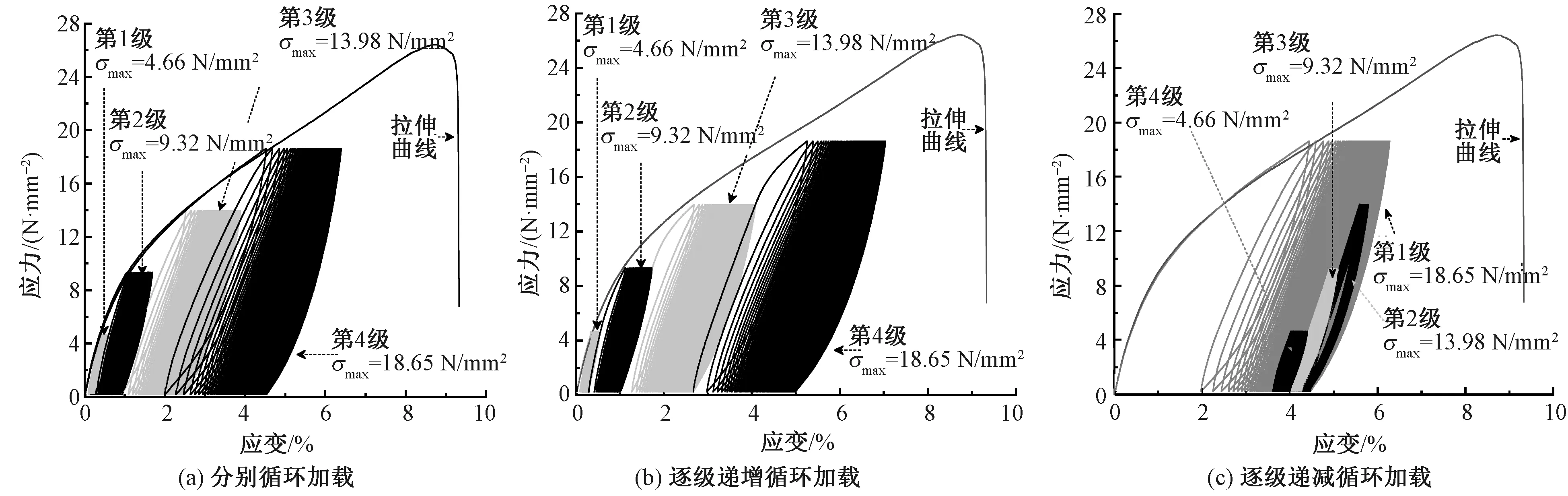
图1 不同循环加载路径下应力-应变曲线Fig. 1 Curves of stress vs. stain under different cyclic loading paths. (a)Constant-amplitude cyclic loading; (b) Stepwise increasing cyclic loading; (c) Stepwise decreasing cyclic loading

由图1可知,多级(逐级递增和逐级递减)循环加载路径下的首级(第1级),其本质上为分别循环加载,虽因试样间存在个体差异,但其循环加载曲线与同等循环峰值应力σmax时的分别循环加载曲线几近重合。相对于同等循环峰值应力的分别循环加载,多级循环加载非首级(第2～4级)的循环加载曲线与之相似,但各级中第1次循环的加载起点存在差异;此外,由各次循环加载和卸载曲线构成的滞回环也存在显著差异。

为深入分析循环加载路径对非首级循环加载曲线形态及各次循环加载起点和卸载终点的影响,以循环峰值应力σmax为13.98 N/mm2时的循环加载曲线为分析对象(见图2),进行进一步研究。分析发现,3种循环加载路径下,非首级且同等循环峰值应力(σmax=13.98 N/mm2)时,不同于分别循环加载各级加载始于0位移点;多级循环加载时各非首级加载始于非0位移点。

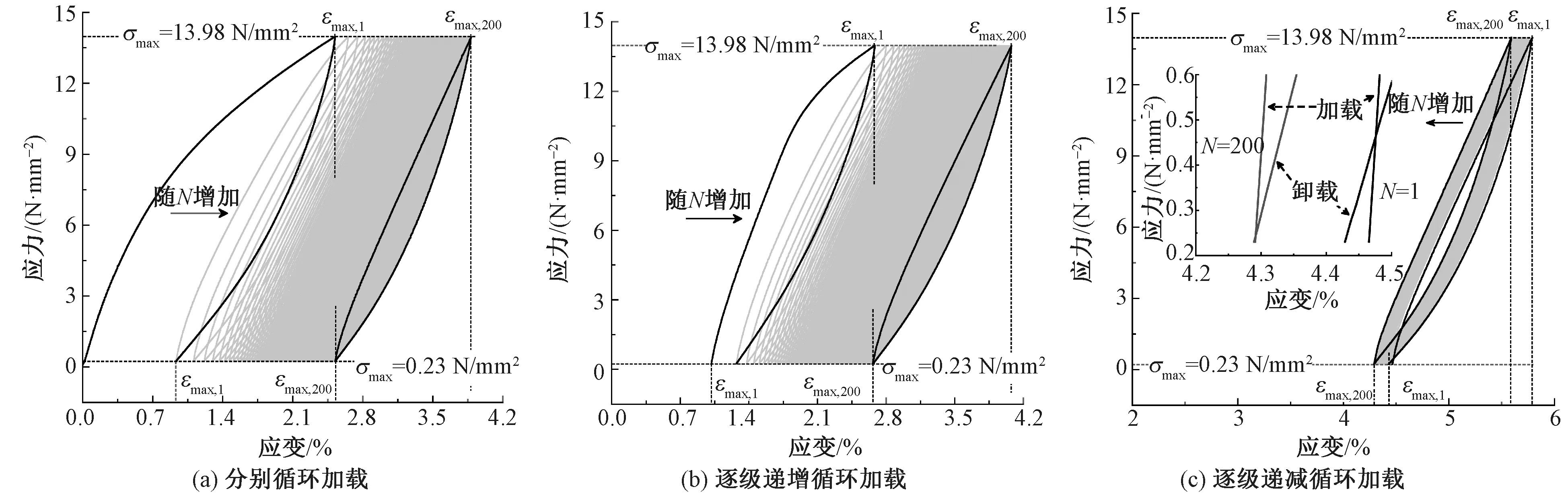
图2 代表性循环阶段的应力-应变曲线(σmax=13.98 N/mm2)Fig. 2 Curves of stress vs. strain under typical cyclic loading stage (σmax=13.98 N/mm2).(a)Constant-amplitude cyclic loading; (b) Stepwise increasing cyclic loading; (c) Stepwise decreasing cyclic loading

图2还表明,3种循环加载路径下,非首级各次循环的加载起点和卸载终点均不重合,加载和卸载曲线构成的滞回环不封闭;且随循环加载的持续进行,各次循环的应力应变曲线趋于均匀致密并重合,整体上呈现先疏后密的变化形式,各次循环的加载起点和卸载终点均趋于接近,但不同循环加载路径下加载起点和卸载终点接近方式存在差异。

分别循环加载路径下,因试样均从0位移点开始加载,故而其各级第1次循环的加载起点均为0位移点。试样处于恒定循环峰值应力的反复拉伸过程,高分子材料中大分子链均处于反复拉伸、回复过程,在拉伸阶段,大分子链间将产生不可逆的滑移,并同时伴随纤维断裂、纱线中纤维间相对位置变化、增强织物几何形态改变,基体开裂以及增强纤维与基体界面脱黏等现象;此外,卸载过程试样回复时大分子链之间、纤维之间存在相互空间位阻作用,导致拉伸阶段产生的变形不可完全回复,从而产生不可逆的残余变形,宏观表现为卸载终点始终位于加载起点的右侧(见图2(a)),卸载终点应变始终高于加载起点应变。随循环加载的持续进行,试样可产生的不可逆变形量逐渐减少,宏观表现为加载起点和卸载终点趋于接近,滞回环曲线趋于封闭,相邻2次的循环加载曲线接近重合。

逐级递增循环加载路径下,材料在各级受力历史与分别循环加载时类似,变形机制一致,各级循环加载曲线特征与对应循环峰值应力分别循环加载时的曲线高度相似。但第i(i≥2)级时其力学行为受前级(第i-1级)加载历史的影响,试样在第i-1级产生的累积残余变形基础上再次循环加载,故而第i(i≥2)级的起点应变并不为0(见图2(b))。

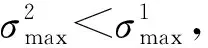
值得注意的是,分别循环加载和逐级递增循环加载路径下,试样在各级均处于逐渐伸长状态,与短纤维增强热塑性复合材料相似[20],均表现出循环软化特性。逐级递减循环加载路径下,试样在首级加载过程中亦表现出逐渐伸长的变化趋势,即亦表现出循环软化特性;但在后续各级加载阶段,试样处于逐渐回复状态,表现出循环硬化特性。

2.2 累积变形特性

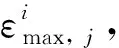
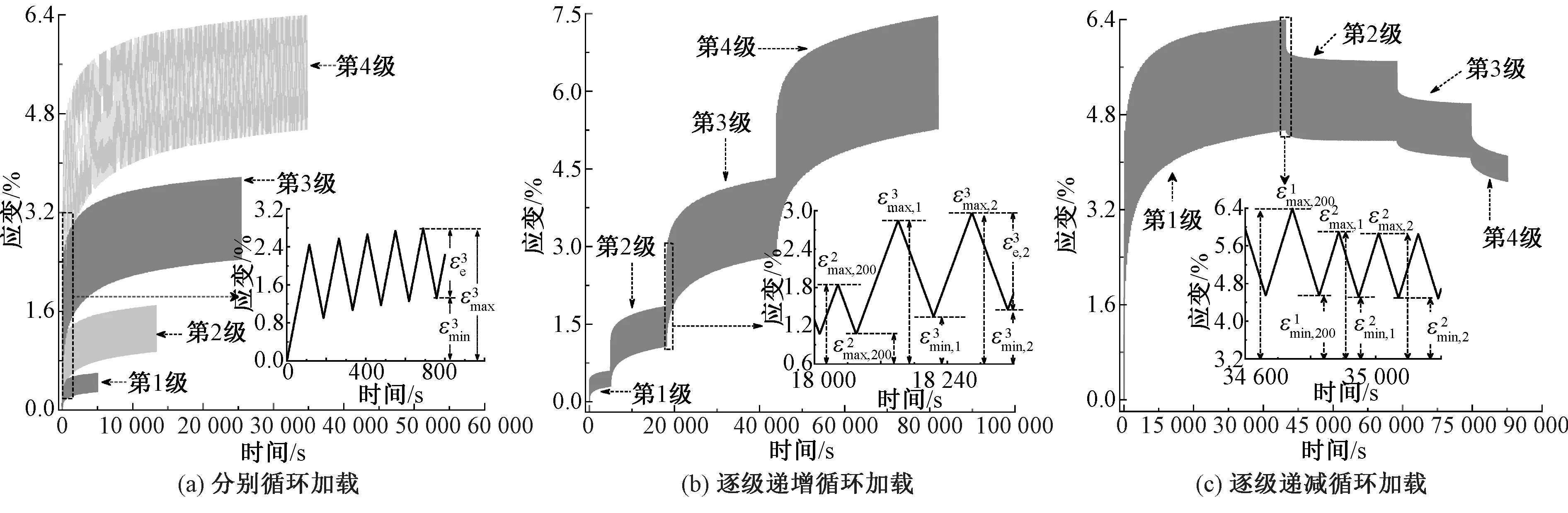
图3 不同循环加载路径下的应变时间曲线Fig. 3 Curves of strain-time under different cyclic loading paths.(a)Constant-amplitude cyclic loading; (b) Stepwise increasing cyclic loading; (c) Stepwise decreasing cyclic loading

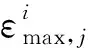
图4 累积加载应变与累积残余应变曲线Fig. 4 Curves of accumulative loading strain (a) and accumulative residual strain (b) with loading cycles

由图4可知,多级(逐级递增与逐级递减)循环加载的首级,试样的累积应变曲线与同等循环峰值应力的分别循环加载时基本重合。逐级递增循环加载路径下,试样在各级时的累积应变曲线相似,均表现为快速增加并逐渐稳定;而逐级递减循环加载路径下,各非首级时试样的累积应变曲线形态与首级相反,表现出快速减少并逐渐稳定的变化趋势。

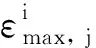
(1)

(1≤i≤4,1≤j≤200)

(2)

(1≤i≤4,1≤j≤200)

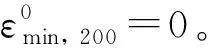
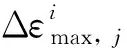
图5 不同循环加载路径下各级累积加载应变与累积残余应变曲线Fig. 5 Curves of accumulative loading strain and accumulative residual strain under different cyclic loading paths. (a)Constant-amplitude cyclic loading; (b) Stepwise increasing cyclic loading; (c) Stepwise decreasing cyclic loading

进一步分析发现,非首级且同等循环峰值应力时,相对于分别循环加载,逐级递增循环加载路径下试样表现出较高的累积应变(见图4),但各级累积应变相对较低(见图5)。究其原因,主要在于前级循环加载过程中,试样已产生一定的残余变形,导致后续各级循环加载时试样可产生的残余变形量减少所致。

2.3 各次循环变形特性与应变回复系数

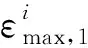
(3)

(4)

(5)

(1≤i≤4, 1≤j≤200)

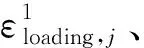
(6)

(7)

(8)

(2≤i≤4,1≤j≤200)

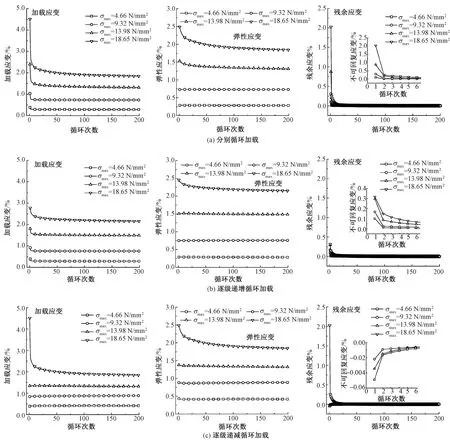
图6 各级各次循环的加载应变、弹性应变及残余应变曲线Fig. 6 Curves of loading strain, elastic strain and residual strain under different cyclic loading paths. (a)Constant-amplitude cyclic loading; (d) Stepwise increasing cyclic loading; (c) Stepwise decreasing cyclic loading

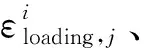
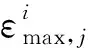
(9)

(1≤i≤4,1≤i≤200)

(10)

(1≤i≤4,1≤i≤200)

不同循环加载路径下试样的应变回复系数曲线如图7所示。可知,试样处于3种循环加载路径下表现出的应变回复系数变化规律存在差异,但均随循环加载的持续进行而逐渐接近100%。

图7 不同循环加载路径下各级应变回复系数曲线Fig. 7 Strain recovery coefficient curves of each stage under different cyclic loading models. (a)Constant-amplitude cyclic loading; (b) Stepwise increasing cyclic loading; (c) Stepwise decreasing cyclic loading

3 结 论

本文以热压法制备的黄麻织物/聚乙烯复合材料为研究对象,对其在3种循环加载路径下的变形行为特性进行了测试和分析,得出以下主要结论。

1)黄麻织物/聚乙烯复合材料的累积应变规律不仅受循环峰值应力大小和循环次数的影响,同时还与循环加载路径密切有关。考虑循环加载路径对材料变形特性的影响,可更好地反映其在实际使用条件下的长期性能,进而获得更具实际意义的结论。

2)分别循环加载和逐级递增循环加载路径下,黄麻织物/聚乙烯复合材料在各级加载阶段均表现出循环硬化特征,但处于逐级递减循环加载路径下时,在首级亦表现出循环硬化特性,但在后续各级却表现出持续的循环软化特征。

3)相对于分别循环加载,逐级递增循环循环加载路径对黄麻织物/聚乙烯复合材料累积应变量、各次循环应变量以及应变回复系数的影响显著,但不改变其变化规律;而逐级递减循环加载路径,将同时影响材料在非首级的累积应变量、各次循环的应变量及应变回复系数,并改变其变化规律。

本文仅考虑黄麻织物/聚乙烯复合材料在不同循环加载路径下的变形行为特征,若全面研究该类材料在复杂受力历史下的力学行为特性,需就不同循环加载速率、随机循环峰值应力下的变形以及能量耗散等特性开展深入研究。