六基色纤维混纺构建的全色相混色模型及其色纺纱纺制

孙显强, 薛 元, 刘曰兴, 张国清, 刘立霞

(1. 江南大学 纺织科学与工程学院, 江苏 无锡 214122; 2. 愉悦家纺有限公司, 山东 滨州 256600)

将染色纤维、原液着色纤维、天然色纤维以及结构生色纤维混纺生产彩色纱和色织面料与服装,是一种短流程、低排放和环境友好型生产工艺技术[1-3]。传统纺织品的染色与印花,是通过调控不同染料的混色比来调制染液或色浆,再对织物进行染色、印花工艺。与传统纺织品的染色、印花工艺不同,彩色纺纱是将织物染色、印花工艺前移,先对纤维进行染色或着色,然后通过纤维自身所具有的色彩经纺纱工序混合后生产具有各种色彩的色纺纱及色织产品,并通过调控不同颜色纤维的混纺比来调控色纺纱及色织产品的色彩及其分布。

染液染色技术通过调控多元基色染料的混合比调制染液进行任意色彩的染色,或者通过调控多元基色色浆的混合比调制墨水进行数码印花[4]。例如,用于染色的自动滴液机电子配液系统,可以根据设计色彩进行自动调控配液比并染出预定的织物色彩;用于数码印花机的电子喷墨系统,可以依据照片像素的色彩自动调控多基色墨水混合比并高还原度的打印出照片色彩。因此,本文模仿染液配色过程构建类似的纺纱自动配色系统,通过彩色纤维混纺比的自动调控纺制出预定色彩的纱线。

色纺产品的色彩视觉风格是通过几种不同纤维的原生色彩空间并置混合再由视神经传递至大脑形成的[5-6]。不同纤维的原生色经空间并置混合,可能会达成较好的色彩融合度,形成一种新的稳定且均衡的色彩混合效应,当几种不同原生色纤维之间有明显的边界,会形成不稳定的多色夹花效应。通过选择色差较小的原生色并运用合理的混纺方式可使不同原生色纤维实现均匀的纤维级混合,实现融合度较好的混合色彩。在这种条件下,可利用多原基色混色原理选择类似色或者近似色纤维以不同的比例进行混纺,实现色纺纱产品的色彩调控、配色及创新。

借鉴染色染液和印花色浆配色技术的思路研究色纺纱产品的配色,首先需要构建全色相调控色纺纱产品的数字化颜色模型,借助大数据原理构建原生色纤维网格化混合模式、基于网格化混合过程色彩的传递规律构建色彩混合模型、再基于混色色立体构建网格点坐标与混合色彩的对应关系并进一步明晰混色比例与原生色纤维混合色彩之间的关系;其次是需要构建彩色纤维的数字化自动化混色装备,如两通道数控纺纱可以通过调控两通道牵伸比实现对成形纱线的色纤维混纺比调控,也能基于成形纱线的色纤维混纺比调控两通道牵伸比[7-8]。将两者结合起来,可以通过调控多元基色纤维混纺比来调控成形纱线的色彩,也能基于纱线色彩确定多元基色纤维混纺比,再通过调控两通道牵伸比纺制预定混纺比的纱线。通过将两通道数控纺纱调控多元基色纤维混合比的机制与多元基色纤维的全色相网格化混纺模型相结合,构建“多通道数控细纱机牵伸比、多元基色纤维混纺比、成形纱线色彩”三要素的协同调控机制,是实现彩色纱纺制的关键[9]。

本文选择色相差为60°左右的相邻色纤维或明度及彩度等级差小于±0.3左右的纤维作为混纺用六元基色纤维,基于二元耦合混色模式并以10%为混色比梯度构建了色相调控范围为0～360°的全色相色纺模型,研究全色相颜色矩阵及其混色色谱的构建方法;结合数控两通道纺纱技术,基于构建的全色相色纺模型研究六基色纤维全色相色纺纱的成纱机制,设计成纱工艺并纺制60个色相的色纺纱,为验证相关理论打基础。

1 全色相混色模型构建及其混色色谱

1.1 六基色纤维及其颜色值的获取

经染色获取彩色纤维α、β、γ、δ、ε、ω,设六元彩色纤维的质量分别为Wα、Wβ、Wγ、Wδ、Wε、Wω,由分光测色仪获取六基色纤维的颜色值分别为Cα(Rα,Gα,Bα)、Cβ(Rβ,Gβ,Bβ)、Cγ(Rγ,Gγ,Bγ)、Cδ(Rδ,Gδ,Bδ)、Cε(Rε,Gε,Bε)、Cω(Rω,Gω,Bω)。

1.2 六基色纤维的离散化质量

将六基色纤维的质量分别进行如下离散化处理,可得到以下6组数列。式中i=1,2,3,…,10,11。

(1)

1.3 基于六基色的二元耦合混色模式构建

令Wα=Wβ=Wγ=Wδ=Wε=Wω,则由式(1)构建两两组合的二元耦合混色模式如下(式中i=1,2,3,…,10,11)。

(2)

设Wα～β(i)、Wβ～γ(i)、Wγ～δ(i)、Wδ～ε(i)、Wε～ω(i)、Wω～α(i)等6组两两组合耦合混色样的混色比分别为[Kα(i),Kβ(i)]、[Kβ(i),Kγ(i)]、[Kγ(i),Kδ(i)]、[Kδ(i),Kε(i)]、[Kε(i),Kω(i)]、[Kω(i),Kα(i)],基于式(2)可得到与每组耦合混色样对应的混色比(式中i=1,2,3,…,10,11)。

(3)

设6组两两组合耦合混色样的颜色值分别为Cα～β(i)、Cβ～γ(i)、Cγ～δ(i)、Cδ～ε(i)、Cε～ω(i)、Cω～α(i),基于式(3)可得到与每组耦合混色样对应的颜色值如下(式中i=1,2,3,…,10,11)。

(4)

设六基色纤维α、β、γ、δ、ε、ω颜色值分别为Cα(255,0,0)、Cβ(255,255,0)、Cγ(0,255,0)、Cδ(0,255,255)、Cε(0,0,255)、Cω(255,0,255),根据式(4)可得到6组耦合混色样色谱(如图1所示)。

图1 二元耦合混色样色谱Fig. 1 Binary coupling color mixing chromatography

1.4 全色相混色模式构建

基于式(1)构建的全色相耦合混色模型如下(式中ξ=1,2,3,…,59,60)。

(5)

当ξ=1,2,3,…,9,10时,Wx=Wα,Wy=Wβ;

当ξ=11,12,…,19,20时,Wx=Wβ,Wy=Wγ;

当ξ=21,22,…,29,30时,Wx=Wγ,Wy=Wδ;

当ξ=31,32,…,39,40时,Wx=Wδ,Wy=Wε;

当ξ=41,42,…,49,50时,Wx=Wε,Wy=Wω;

当ξ=51,52,…,59,60时,Wx=Wω,Wy=Wα。

且W(ξ) 完成Wα⟹Wβ⟹Wγ⟹Wδ⟹Wε⟹Wω⟹Wα的变化过程。由此得全色相混色样的质量。

(6)

1.5 全色相耦合混色样的混色比

设λ(ξ)=[λx(ξ),λy(ξ)]为全色相混色过程各混色样混合比,则基于式(5)可得:

(7)

或:

(8)

1.6 全色相耦合混色样的颜色值

设C(ξ)=[R(ξ),G(ξ),B(ξ)]为全色相混色过程各混色样颜色值,则基于式(7)可得:

(9)

或:

(10)

基于式(10)可得到全色相混色样的矩形色谱(见图2)。

图2 全色相矩形色谱Fig. 2 Full color phase rectangular chromatography

1.7 圆环状全色相混色模型的构建

根据图2将全色相矩阵色谱首尾拼接可得到全色相环形色谱(如图3所示)。

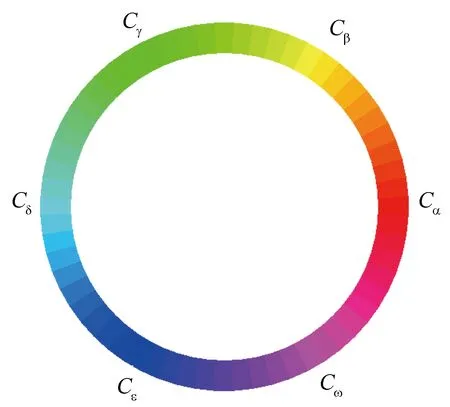
图3 全色相环形色谱Fig. 3 Full color phase circular chromatography

2 全色相色纺纱两通道数控纺纱原理

2.1 两通道数控纺纱系统

数控纺纱是以多根粗纱异步牵伸(多个通道)为本质特征,对所纺制纱线的混色比、线密度及捻度的变化进行在线调控的纺纱方法,其设备如图4所示,分别示出2种不同色纱混纱时的实物图。对于数控纺纱而言,一个完整的系统包括纺纱机械系统、纺纱控制系统和纺纱伺服系统。纺纱机械系统包括多通道耦合数码纺纱机的耦合牵伸机构、加捻机构和卷绕成形机构;纺纱控制系统包括上位机触摸屏、下位机及控制程序;纺纱伺服系统包括与机械系统各机构对应的伺服电动机、变频电动机及其伺服驱动器、变频器、编码器、减速器等组成。

图4 数控纺纱系统实物图Fig. 4 Image of numerical control spinning system. (a) Color mixing of roving red and yellow; (b) Color mixing of roving yellow and green; (c) Color mixing of roving green and cyan; (d) Color mixing of roving cyan and blue; (e) Color mixing of roving blue and magenta; (f) Color mixing of roving magenta and red

2.2 两通道数控纺纱成形参数

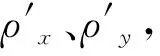
1)两通道牵伸比。两通道牵伸比如下:

(11)

令ρx=ρy=ρ,则式(11)简化为

(12)

2)成纱线密度。在两通道混色数控纺纱系统中,2根粗纱经2个独立驱动的后罗拉喂入,则在前罗拉钳口汇合并进入加捻机构进行加捻形成的两通道色纺纱的线密度ρs为

(13)

3)成纱混纺比。在两通道混色数控纺纱系统中,将2根异步牵伸得到的须条合并加捻形成纱线,各须条在成纱中的混纺比λx、λy为

(14)

λx+λy=1

(15)

4)成纱颜色。假定成纱颜色由各粗纱条的颜色值及其混纺比决定,则成纱颜色Cs=[Cr,Cg,Cb]T为

(16)

3 全色相混色模型的色纺纱纺制原理

3.1 基于纱线色彩获取两基色纤维混纺比

假定成纱颜色为Cs(ξ)=[R(ξ),G(ξ),B(ξ)],且已知两通道粗纱的色彩为Cx(Rx,Gx,Bx),Cy(Ry,Gy,By),由式(9)可得混纺比参数。

(17)

3.2 基于纱线混纺比的两基色纤维牵伸比

假设两基色纤维对应的粗纱线密度为ρx、ρy,颜色分别为Cx(Rx,Gx,Bx)、Cy(Ry,Gy,By),前罗拉线速度为Vq(ξ),2个后罗拉线速度为Vx(ξ)、Vy(ξ),2个通道牵伸比为Ex(ξ)、Ey(ξ),各须条在成纱中的混纺比为λx(ξ)、λy(ξ),纱线的线密度为ρs(式中ξ=1,2,3,…,59,60)。

则两基色纤维的牵伸比为

(18)

令ρx=ρy=ρ,则式(18)简化为

(19)

由此可得纺制全色相色纺纱的牵伸比矩阵:

(20)

基于两通道数控纺纱机和六基色粗纱,以相邻色进行两两耦合混纺。由此可得全色相混色样的混纺比,α与β、β与γ、γ与δ、δ与ε、ε与ω、ω与α两基色色纺纱的混纺比均为10∶0、9∶1、8∶2、7∶3、3∶2、1∶1、2∶3、3∶7、1∶4、1∶9,有10个梯度。

两通道数控纺纱所用粗纱的线密度均为450 tex,所纺色纺纱线密度均为27.76 tex,由此可得全色相混色样的牵伸比,α与β、β与γ、γ与δ、δ与ε、ε与ω、ω与α两基色色纺纱的牵伸比均为16.2∶0、18.0∶162.1、20.3∶81.0、23.2∶54.0、27.0∶40.5、32.4∶32.4、40.5∶27.0、54.0∶23.2、81.0∶20.3、162.1∶18.0共10个梯度。

由此可得全色相混色纱的颜色值,如表1所示。

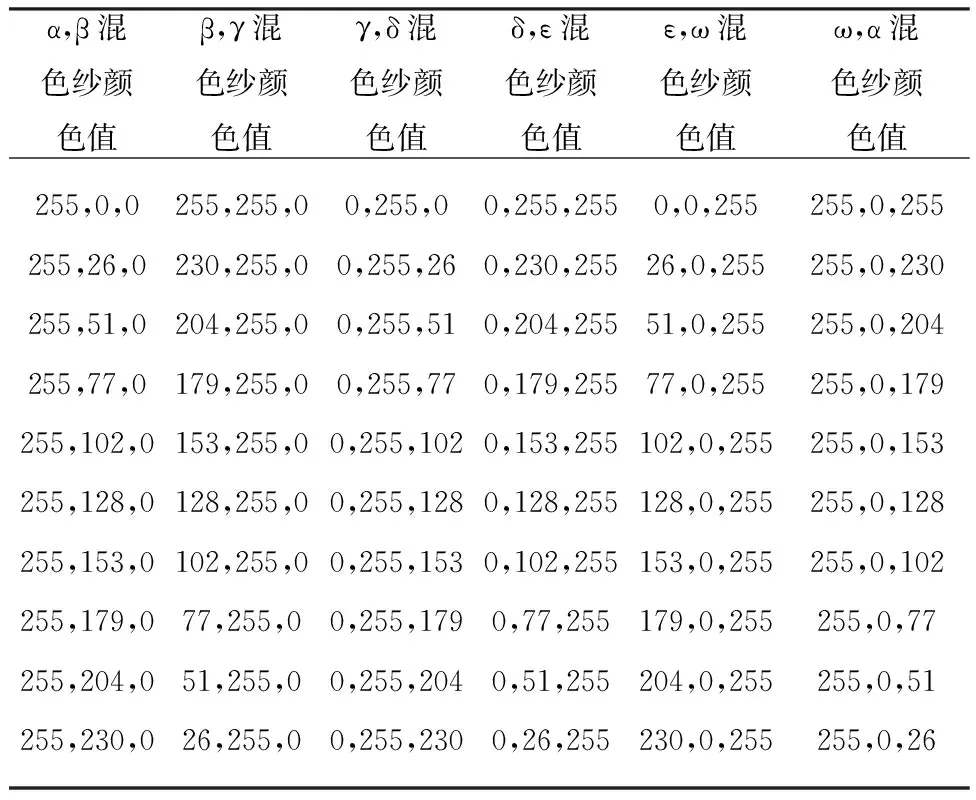
表1 全色相色纺纱的颜色值Tab. 1 Colors of melange yarns in full color phase

通过上述工作,将两通道数控纺纱调控六基色纤维混纺比与六基色纤维全色相网格化混色模型相结合,构建了能协同调控多通道数控细纱机牵伸比-多元基色纤维混纺比-纱线色彩三要素的彩色纺纱机制。

4 实验部分

4.1 色纺纱的纺制

原料为长绒棉,采用活性染料染色分别获得红(R)、黄(Y) 、绿(G)、蓝(B)、青(C)、品红(M)六基色纤维,经过开清棉、梳棉、精梳、并条、粗纱工序获得线密度为450 tex的彩色粗纱。

60种色纺纱的设计线密度均为27.76 tex,纱线捻度均为600捻/m,纱线捻系数均为316.13,纱线的捻向均为Z捻,机器用JWF1551A两通道数控环锭细纱机,锭子的转速为7 500 r/min,前罗拉速度为12.50 m/min,钢领型号为PG1-4254,钢丝圈型号为UDR 5/0,钢领的上升速度为0.8 mm/s,级升距离为0.5 mm,钢领的下降速度为2.5 mm/s。

4.2 基于六基色粗纱实测色彩全色相混色色谱

采用3nh YS6010分光测色仪在D65光源,10°视场,25.4 mm孔径,SCI模式条件下获得纱线的反射率值,每个样品测量5次,取其平均值。由此获得的六基色实测颜色值分别为CR(117,30,44)、CY(220,175,0)、CG(0,98,80)、CC(0,114,135)、CB(35,63,111)、CM(151,20,71),则六基色混色色谱如图5所示。

图5 用于六基色纤维的混色色谱Fig. 5 Color mixing chromatography for six primary colored fibers

4.3 色纺纱的性能测试与表征

色纺纱在标准大气压条件下储存24 h,温度为(20±2)℃,相对湿度为(65±2)%。参照GB/T 3292.1―2008《纺织品 纱线条干不匀试验方法 第1部分:电容法》[10],采用YG133B/Pro-H条干均匀度测试仪测试色纺纱条干均匀度,测试速度为400 m/min,测试的纱线长度为400 m。参照FZ/T 01086―2000《纺织品 纱线毛羽测定方法 投影计数法》[11-12],通过Y172A纱线毛羽测试仪测试色纺纱的毛羽,测试速度为30 m/min,测试段的长度为10 m,测试10次,结果取平均值。采用XL-2纱线强伸度仪测试色纺纱的力学性能,每种纱线样品测试20次,纱线的拉伸速度为500 mm/min,加持距离为500 mm,纱线的预加张力为13.8 cN[13-15]。

4.4 色纺纱织物的制备与色彩值测试

采用HC21K圆筒针织机用上述纱线进行织造,线圈长度为0.6 mm,织物横密为49纵行/(5 cm),纵密为80横列/(5 cm)。采用4.2节中的测试条件,测试60种织物的反射率值,每个样品测量5次,结果取其平均值并换算成颜色值。

5 结果与讨论

5.1 色纺纱织物色彩比较分析

如图6所示,将所得的织物分为11行6列,每行的两基色分别为RY、YG、GC、CB、BM、MR,每行以10%为梯度进行变化的混纺比。以此混纺比变化实现了六基色色彩间的梯度渐变。

图6 色纺纱织物实物图Fig. 6 Image of fabrics woven by melange yarns

基于上述实验结果,将其与图5进行对比,可知基于全色相混色模型60个网格点所定义的六基色纤维混纺比纺制60种混色纱,其色彩变化规律与六基色纤维混纺比变化规律一致,与全色相网格化混色模型的色彩分布规律也具有一致性。与图6对应的织物实测颜色值如表2所示。

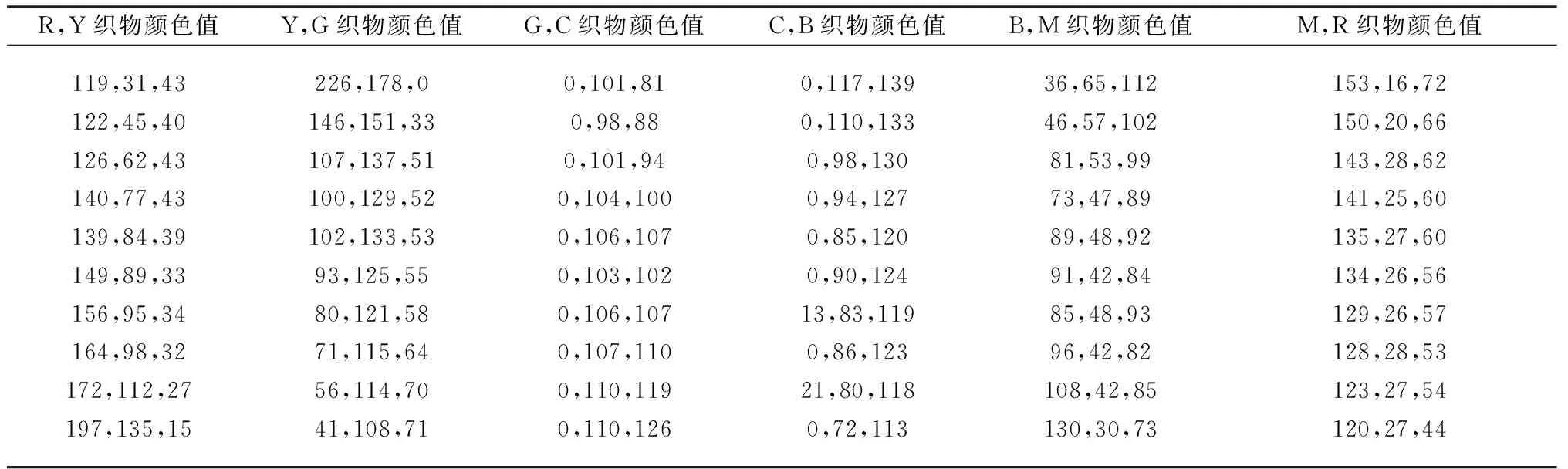
表2 全色相织物的实测颜色值Tab. 2 Measured colors of fabrics in full color phase

5.2 色纺纱外观及力学性能测试分析

对相同混纺比不同色系的纱线的条干不匀率、毛羽、强力的测试结果分别如表3～5所示。

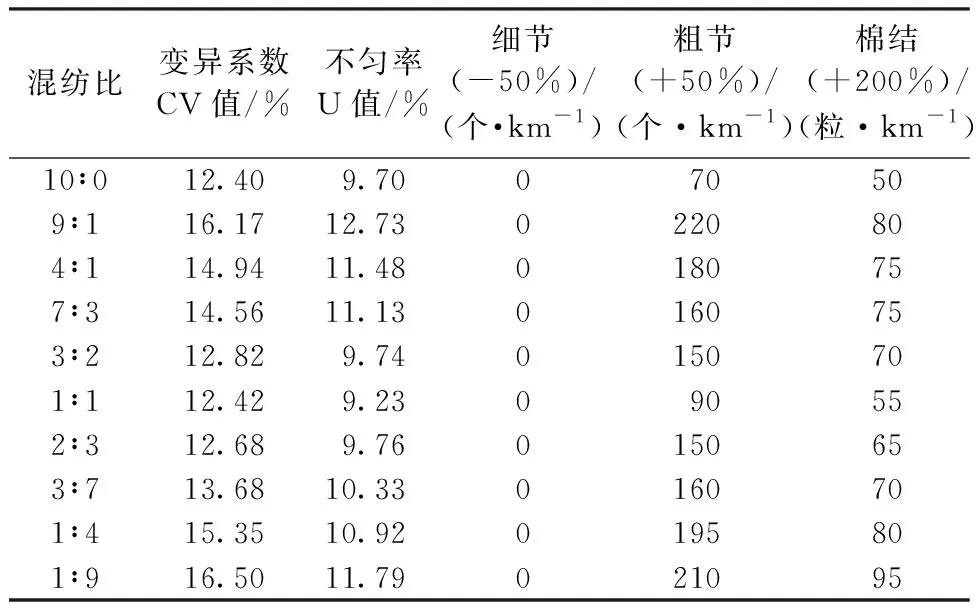
表3 纱线的条干比较Tab. 3 Comparison of yarn unevenness

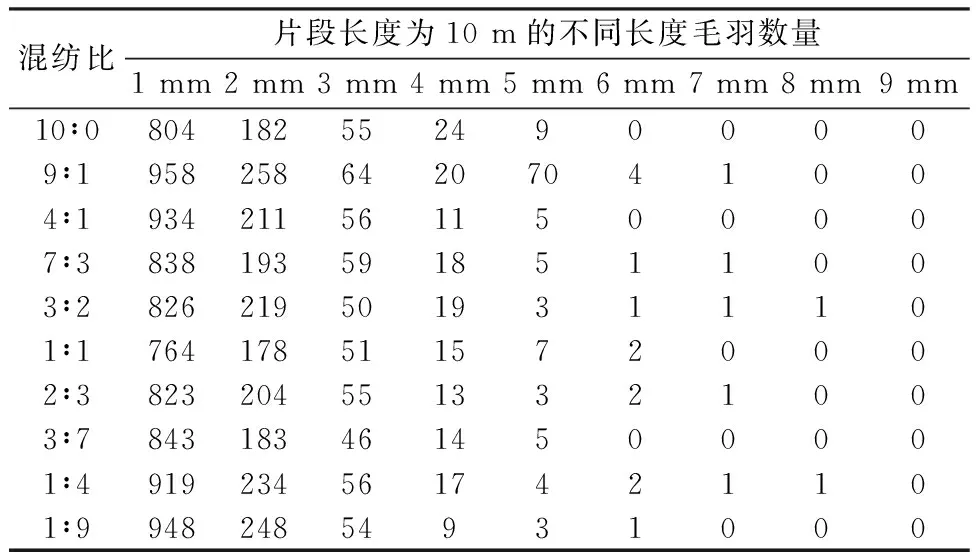
表4 纱线毛羽比较Tab. 4 Comparison of yarn surface hairiness

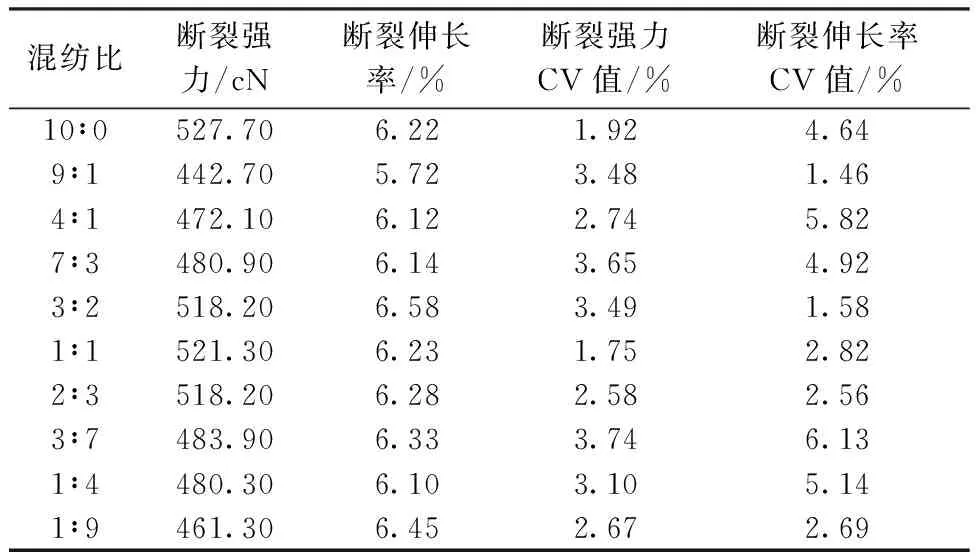
表5 纱线强力比较Tab. 5 Comparison of yarn tensile properties

两通道数控纺纱是通过调控各通道牵伸比来调控混纺比。一般来说,当后区牵伸比小于1.3时属于张力牵伸,这是传统纺纱采用的工艺,它有利于改善纱线条干不匀、改善毛羽和提升强力;当后区牵伸比介于1.3～1.8之间时属于弹性牵伸,不利于改善纱线条干不匀、改善毛羽和提升强力均匀性,是传统纺纱中不鼓励采用的工艺;当后区牵伸比大于1.8时属于位移牵伸,对纱线条干不匀、改善毛羽和强力均具有破坏性作用,是传统纺纱中不可能采用的工艺。由于两通道数控纺纱是通过调控各通道牵伸比来调控混纺比,在纺制某种混色比纱线时,有可能同时存在张力、弹性和位移牵伸中的1种或2种形式的牵伸。综合来看,采用两通道数控方式纺制色纺纱的条干、毛羽及其力学性能的均匀性均低于传统的纺纱模式。

6 结 论

本文选择色相差为60°左右、明度及彩度等级差小于±0.3左右的红(R)、黄(Y) 、绿(G)、蓝(B)、青(C)、品红(M)等六基色纤维,基于二元耦合混色模式构建了色相调控范围为0～360°的全色相混色模型,给出以10%为混色梯度的全色相颜色矩阵及混色色谱;结合数控两通道纺纱机制,基于全色相混色模型探讨了六基色纤维全色相色纺纱的成纱机制。为验证相关理论,设计纺纱工艺并制备了60个色相的色纺纱及其色织物,对60种全色相色纺纱的条干、毛羽、断裂强力等外观质量与力学性能指标进行了测试分析。结果表明,基于全色相混色模型60个网格点所定义的六元基色纤维混色比纺制60种色纺纱,其色彩变化规律与六元基色纤维混纺比变化规律一致,与全色相网格化混色模型的色彩分布规律也具有一致性,验证了本文构建的“两通道数控细纱机牵伸比-六元基色纤维混纺比-纱线色彩”的协同调控机制,对于指导纺制全色相色纺纱具有支撑作用,纺制的60种全色相色纺纱各项指标基本达到GB/T 398—2018《棉本色纱线》二级的要求。