止水帷幕深度对降水井出水流量的影响分析

李 龙 ， 唐金召 ， 左文州 ， 李长印 ， 李景丰

（1.中国水利水电第十一工程局有限公司， 河南 三门峡450001；2.河南理工大学土木工程学院， 河南 焦作450003）

0 引言

近年来， 随着我国城市交通拥挤问题日益突出， 城市地铁交通需求急剧增加， 地铁基坑朝着更深的方向发展， 出现了大量的地铁深基坑工程。基于大量基坑事故调查分析， 其中与地下水相关的事故高达80%［1］。 近几年， 地铁基坑降水施工中因降水及止水帷幕问题引起的安全事故常有发生， 严重影响施工周期和工程经济效益。 因此，如何安全、 有效地实现基坑降水已成为众多专家学者的研究重点。

目前， 国内外诸多学者对止水帷幕深度做过一系列相关研究， 取得了止水帷幕插入深度对周边地下水位变化、 基坑变形、 地表沉降等影响的研究成果。 Zhou 等［2］研究了不同地连墙深度下地下水位的变化， 结果表明： 含水层的降深随地连墙深度的增加而减小； 冯晓腊等［3］提出了落底式止水帷幕综合止水系数， 定义了基坑岩土体表观渗透系数概念， 为定量计算基坑涌漏量和评价止水帷幕效果提供了重要的理论依据； 李伟等［4］研究发现地连墙插入第一层承压含水层深度与坑内外水位变化和地表沉降呈负相关关系， 其趋势为先缓慢减小再显著减小， 最后趋于稳定； Wang等［5］提出了耦合非达西渗流概念， 研究了不同帷幕与降水井组合方式下的耦合效应， 发现滤管长度短、 滤管与地连墙水平距离小等可显著增强止水帷幕与降水井的耦合作用。 Xu 等［6］研究发现随着止水帷幕插入深度比的增加， 止水帷幕两侧的水力梯度增加， 坑外沉降减小； 随着滤管长度比的增加， 止水帷幕两侧的水力梯度减小， 坑外沉降增加； 哈达等［7］研究了不同地连墙深度下坑外地表沉降的变化规律， 基坑外沉降量随着地连墙深度的增加而减少， 实现了不同深度基坑的地连墙深度优化； Wu 等［8］分析了基坑降水过程中止水帷幕发生渗漏造成的影响， 当发生渗漏时， 坑外地下水水头下降较快， 而土体固结缓慢； 王军辉等［9］提出了适用于悬挂式止水帷幕下基坑涌水量计算的修正大井法， 并对悬挂式止水帷幕深度进行了优化； 张志红等［10］提出了安全、 经济的悬挂式止水帷幕基坑控水优化设计方法， 为确定最优帷幕入土深度提供了一种新方法。

上述研究成果主要集中在止水帷幕深度对周边地下水位变化、 地表沉降的影响规律以及止水帷幕深度优化设计等， 而针对不同止水帷幕插入潜水层深度对降水井出水流量影响的研究较少，其相关研究成果发表较少。 因此， 本文结合郑州地铁某车站基坑降水工程， 以现场抽水试验和水文地质参数为基础， 利用MIDAS GTS 软件分析不同止水帷幕插入潜水层深度对降水井出水流量的影响， 并对其影响规律进行分析。

1 工程背景与地质条件

1.1 工程背景

该车站为地下两层岛式站台车站， 车站基坑全长222.8 m， 端头井段宽25.1 m， 标准段宽19.9 m， 基坑开挖深度为17 m。 该车站基坑降水采用降水井＋排水沟＋集水井的方式， 降水共设置22 口降水井， 为坑内降水， 标准段降水井深27 m，扩大端降水井深28 m， 井间距25 m， 降水井孔径800 mm， 管质均采用直径325 mm、 壁厚8 mm 的焊接钢管， 其位置分布如图1 所示。 车站主体基坑围护结构采用直径1000 mm、 间距1500 mm 钻孔灌注桩＋内支撑的支护形式， 基坑外围以直径850 mm、 间距600 mm、 深度25.5 m 三轴搅拌桩作为止水帷幕。

图1 降水井位置图Fig.1 Location chart of precipitation wells

1.2 工程地质与水文地质条件

该地铁车站场地详勘资料揭露深度范围内地层主要为杂填土及第四系上更新统（Q／3） 粉质黏土、 粉土， 第四系中更新统（Q／2） 粉质黏土、 细砂等土层， 现将勘察深度内的土层按其不同的成因、 时代及物理力学性质差异自上而下分为11 个工程地质单元层， 如图2 所示。 为对基坑降水进行三维数值模拟计算， 将相似的土层视作一层，因此， 将计算模型土层简化为7 层， 各土层物理力学参数如表1 所示。

表1 土层物理力学参数Table 1 Physical and mechanical parameters of soil layer

该车站地下水为孔隙潜水， 属于第四纪松散岩类潜水， 另外， 地下水主要补给有大气降水入渗、 地表水下渗、 地下水侧向迳流等。 该车站稳定地下潜水水位主要埋深在10.9 m ～11.6 m （标高97.0 m）， 主要赋存于③36黏质粉土、 ③41粉砂、③37黏质粉土、 ③38黏质粉土、 ③23粉质黏土等土层中， 其含水层厚度约16 m。

2 止水帷幕作用机理

止水帷幕是布置在基坑外围或底部用于阻隔或延缓地下水涌入基坑内的某种构筑物， 如地连墙、 排桩等［11］。 止水帷幕对地下水渗流的阻隔作用体现在三个方面， 即地下水流入的方向由水平转变成水平与垂直的组合， 加长了坑外地下水流入井中的渗流路径， 减小了地下水的渗流面积［12］。图3 为悬挂式、 落地式止水帷幕作用示意图， 可以看出悬挂式止水帷幕不能完全阻隔坑内外的水力联系， 故随着止水帷幕深度的变化， 基坑内外水位、 基坑涌水量、 降水井出水量、 地表沉降等均会发生相应的变化。

3 基坑管井降水有限元数值模拟

3.1 有限元模型的建立

本文采用有限元软件MIDAS GTS 建立基坑降水井降水三维模型， 以此分析不同止水帷幕插入含水层深度对降水井出水流量的影响。 结合车站基坑地质条件（表1 土层力学参数） 及施工设计资料， 建立1 ∶1 基坑降水井三维计算模型。 为有效去除边界不确定性造成计算结果随意的影响，所取有限区域应包括基坑的影响区域， 即从基坑边界到模型边界的尺寸不能小于基坑开挖深度的3倍， 为此， 模型尺寸定义为352.8 m×155.1 m×50 m， 该模型所建实体单元总数为118194 个， 基坑降水三维模型网格划分如图4 所示， 其止水帷幕模型通过界面单元（设置渗透系数为0 的界面材料） 实现。

图4 基坑降水三维模型示意图Fig.4 Three-dimensional model of foundation pit dewatering

土层模型采用修正摩尔库伦本构， 修正摩尔库伦是一种将非线弹性和塑性联合起来的组合模型， 考虑了土体的剪胀性， 并引入屈服盖帽（Cap）， 土体刚度随应力变化而变化， 可以模拟包括软土和硬土在内的不同类型的土体行为的弹塑模型。 基坑降水模型顶部位移边界条件设置为自由边界， 模型四周设置水平位移约束， 模型底部设置x、 y、 z 方向的位移约束； 该三维计算模型通过设置节点水头来模拟基坑水位变化， 根据现场勘察数据设置基坑内初始总水头为-10.9m， 降水后的总水头为-18.9m， 降水井内水位变化采用渗流边界函数（水位与时间的变化关系， 根据现场实测数据设置）。

3.2 模型验证

为较好的反应实际工程情况， 需将模型模拟结果与现场抽水试验实际数据进行对比， 根据现场降水井实测数据， 改变模型的节点水头边界条件， 进而对模型及相关参数进行修正， 直至所建模型与实际情况基本保持一致。 本次抽水试验选取降水井位置图（图1） 中的JS4、 JS6 为观测井，JS5 为抽水井， 其降水时间共33 d。

按4.1 节内容建立计算模型， 得到止水帷幕深度25.5 m、 降水时间33 d 的基坑内、 外水位等值线变化云图， 如图5、 图6 所示。 从图5 可以看出， 基坑外部水头由基坑向外逐渐减小； 由图6可知， 基坑内水位降低至-18 m 以下， 满足基坑施工开挖要求， 上述模拟计算结果与抽水试验实测数据较为接近。 本文选取众多降水井中的JS5 抽水井实测数据与模拟计算结果进行对比拟合， 降水井水位降深模拟结果与实测结果对比分析如图7所示， 水位降深模拟结果与实测结果基本一致，因此， 可以认为该三维模型能够较好地模拟基坑降水过程中的真实情况。

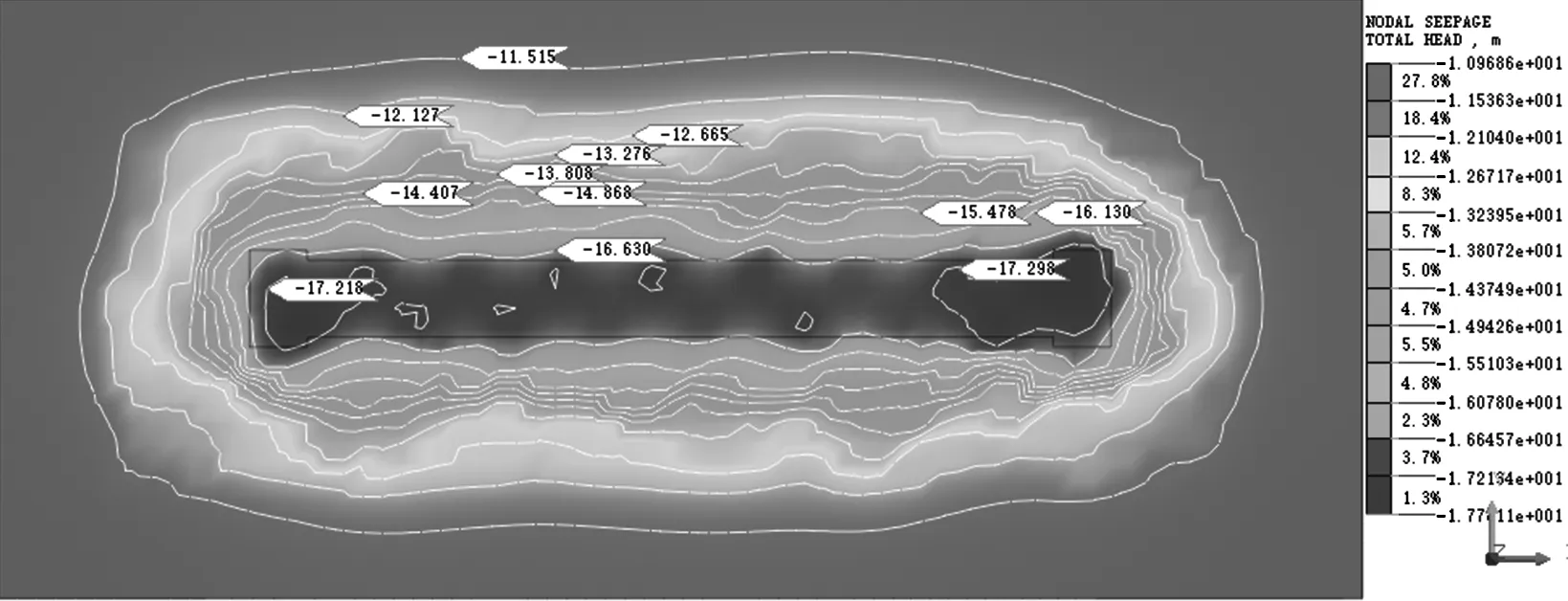
图5 坑外水位等值线变化云图Fig.5 The contour change cloud of water level outside the pit

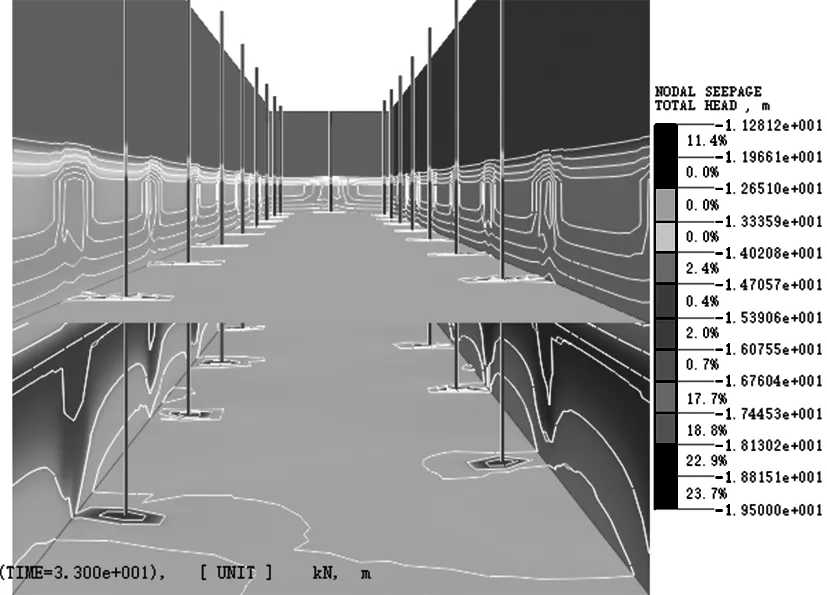
图6 坑内水位等值线变化云图Fig.6 Cloud image of water level contour change in pit

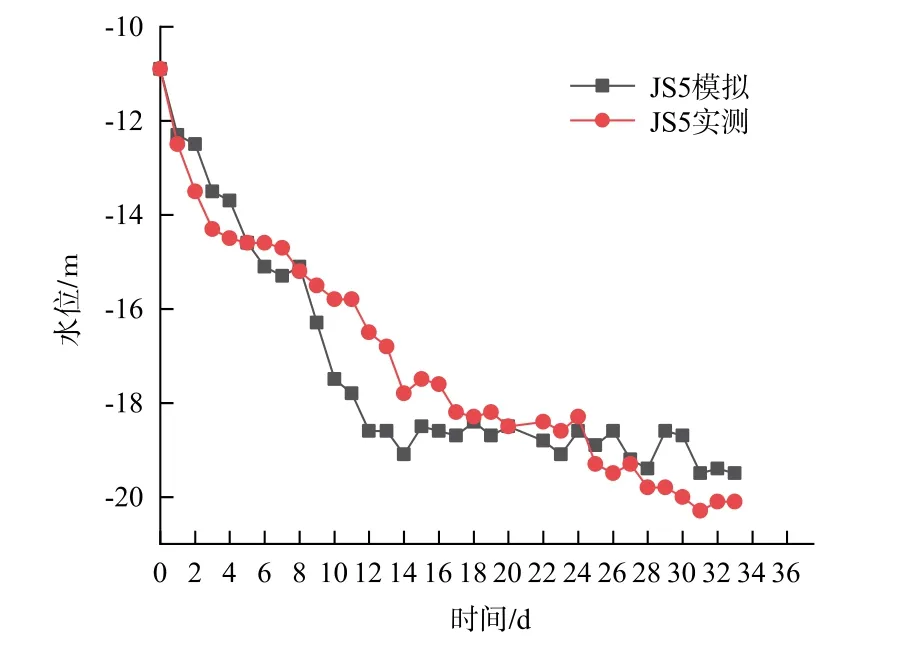
图7 水位变化实测曲线与模拟曲线对比图Fig.7 Comparison chart of measured curve and simulated curve of water level change

3.3 基坑管井降水模拟结果分析

本文以基坑实际止水帷幕深度、 上述修正模型为基础， 通过调整止水帷幕插入潜水层深度，以研究不同止水帷幕深度下降水井出水流量的变化规律。 本次模拟采用控制变量法， 在土体参数、渗流边界条件、 位移边界条件等其他条件不变的情况下， 设置不同深度的止水帷幕， 对比分析各种工况下降水井出水流量的变化， 不同工况下止水帷幕插入含水层深度见表2。

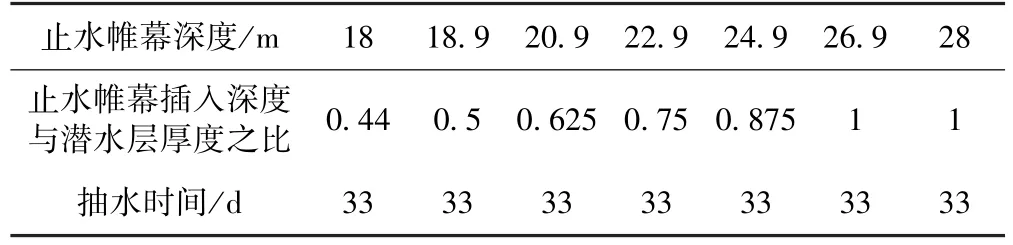
表2 模型计算工况Table 2 Model calculation conditions

图8 为不同止水帷幕深度下基坑内流量云图，由图8 可以发现， 坑内流量随着止水帷幕深度的增加而减小， 尤其是当止水帷幕深度由18 m 增大到20.9 m 时， 坑内流量变化幅度较大， 降低了16.56%， 止水帷幕的阻隔效应显著。 根据MIDAS GTS 的数值模拟结果， 绘制出降水井出水流量与止水帷幕深度变化的对应关系曲线， 如图9 所示（保持基坑内水位降深1.9 m 及其他降水条件不变的情况下）。 由图9 曲线可知， 在基坑内水位降深保持1.9 m 的条件下， 止水帷幕插入含水层的深度与降水井出水流量呈现出负相关关系， 即随着止水帷幕插入潜水层深度的增大， 降水井出水流量逐渐减小， 当贯穿潜水层后逐渐趋于稳定； 当止水帷幕插入比介于0.44～0.625 之间时， 随着止水帷幕插入深度的增加降水井出水量变化幅度逐渐减小， 在插入比为0.5 时出现拐点， 降水井出水流量的降低幅度发生显著变化， 前后减小幅度分别为13.20%、 3.87%， 其主要原因是止水帷幕深度在大于18.9 m （降水后总水头-18.9 m） 后， 止水帷幕开始形成有效隔水边界， 止水帷幕的隔水效应逐渐显现， 对基坑渗流场产生较大的影响；当止水帷幕插入比在0.625 ～0.875 之间时， 降水井出水流量近似线性的减小， 其减小幅度较为均匀， 分别为6.95%、 7.66%， 可见利用止水帷幕阻隔坑内外水力联系可有效降低降水井出水流量；当止水帷幕插入比大于0.875 时， 降水井出水流量降低幅度较小， 随着止水帷幕完全隔断潜水含水层， 降水井出水流量基本趋于稳定状态， 且降水井出水流量降低的效果与完全隔断含水层的效果相近。 因此， 为了降低降水井出水流量， 应增大止水帷幕深度， 但为了考虑工程项目的经济性而不能一直增大， 故基于上述分析可在0.875 ～1 之间选取止水帷幕插入比深度。

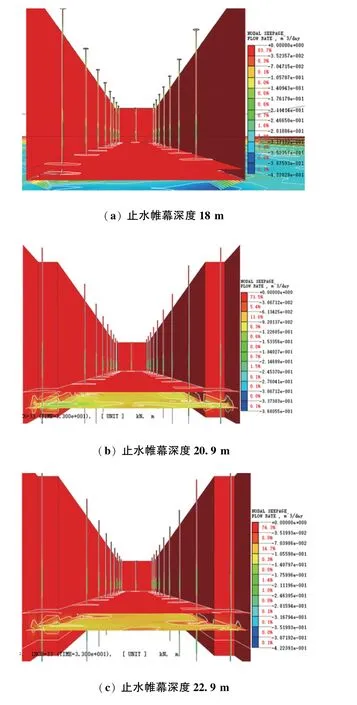
图8 不同止水帷幕深度流量图Fig.8 Flow chart of different waterproof curtain depth

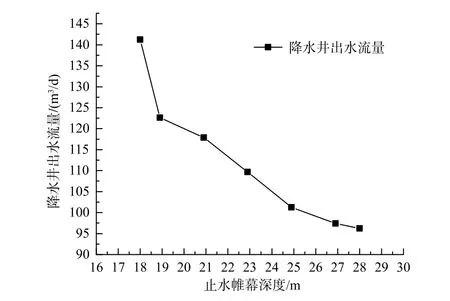
图9 降水井出水流量与止水帷幕深度变化关系曲线Fig.9 Curve of relationship between outflow rate of dewatering well and depth of waterproof wall

4 结论

以郑州地铁某车站基坑降水工程为例， 通过MIDAS GTS 模拟结果与实测数据对比， 结合理论分析， 研究了三轴搅拌桩止水帷幕插入潜水层不同深度下降水井出水流量的变化规律， 得到如下结论：

（1） 止水帷幕插入潜水层的深度与降水井出水流量呈负相关， 即降水井出水流量随着止水帷幕插入潜水层深度的增大逐渐减小， 当贯穿潜水层后基本趋于稳定状态。

（2） 当止水帷幕插入比介于0.44 ～0.625 时，降水井出水流量的变化幅度随止水帷幕插入深度的增加逐渐减小， 且在插入比为0.5 时出现拐点，降水井出水流量的降低幅度发生显著变化； 当止水帷幕插入比在0.625 ～0.875 之间时， 降水井出水流量近似线性的减小， 可见利用止水帷幕阻隔坑内外水力联系可有效降低降水井出水流量。

（3） 当止水帷幕插入比大于0.875 时， 降水井出水流量降低的效果与完全隔断含水层的效果相近， 基于不同止水帷幕深度对降水井出水流量的影响与造价成本的综合考虑， 止水帷幕插入比深度可介于0.875～1 之间。